Argument Estimates of Multivalent Functions Involving a Certain Fractional Derivative Operator ()
1. Introduction
Let 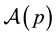 denote the class of functions
denote the class of functions 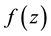 of the form
of the form
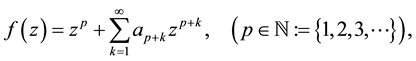 (1.1)
(1.1)
which are analytic in the open unit disk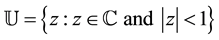 . Also let
. Also let 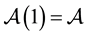 denote the class of all analytic functions
denote the class of all analytic functions 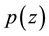 with
with 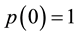 which are defined on
which are defined on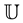 .
.
Let a, b and c be complex numbers with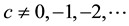 . Then the Gaussian hypergeometric function
. Then the Gaussian hypergeometric function 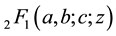 is defined by
is defined by
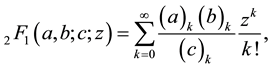 (1.2)
(1.2)
where 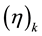 is the Pochhammer symbol defined, in terms of the Gamma function, by
is the Pochhammer symbol defined, in terms of the Gamma function, by
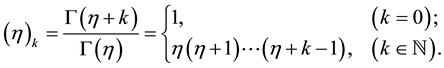
The hypergeometric function 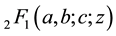 is analytic in
is analytic in 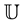 and if a or b is a negative integer, then it reduces to a polynomial.
and if a or b is a negative integer, then it reduces to a polynomial.
There are a number of definitions for fractional calculus operators in the literature (cf., e.g., [1] and [2] ). We use here the Saigo type fractional derivative operator defined as follows ([3] ; see also [4] ):
Definition 1. Let 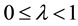 and
and![]() . Then the generalized fractional derivative operator
. Then the generalized fractional derivative operator ![]() of a function
of a function ![]() is defined by
is defined by
![]() (1.3)
(1.3)
The function ![]() is an analytic function in a simply-connected region of the z-plane containing the origin, with the order
is an analytic function in a simply-connected region of the z-plane containing the origin, with the order
![]()
for![]() , and the multiplicity of
, and the multiplicity of ![]() is removed by requiring that
is removed by requiring that ![]() to be real when
to be real when![]() .
.
Definition 2. Under the hypotheses of Definition 1, the fractional derivative operator ![]() of a function
of a function ![]() is defined by
is defined by
![]() (1.4)
(1.4)
With the aid of the above definitions, we define a modification of the fractional derivative operator ![]() by
by
![]() (1.5)
(1.5)
for ![]() and
and![]() . Then it is observed that
. Then it is observed that ![]() also maps
also maps ![]() onto itself as follows:
onto itself as follows:
![]() (1.6)
(1.6)
It is easily verified from (1.6) that
![]() (1.7)
(1.7)
Note that![]() ,
, ![]() and
and![]() , where
, where ![]() is the fractional derivative operator defined by Srivastava and Aouf [5] .
is the fractional derivative operator defined by Srivastava and Aouf [5] .
In this manuscript, we drive interesting argument results of multivalent functions defined by fractional derivative operator![]() .
.
2. Main Results
In order to establish our results, we require the following lemma due to Lashin [6] .
Lemma 1 [6] . Let ![]() be analytic in
be analytic in![]() , with
, with ![]() and
and ![]()
![]() . Further suppose that
. Further suppose that ![]() and
and
![]() (2.1)
(2.1)
then
![]() (2.2)
(2.2)
We begin by proving the following result.
Theorem 1. Let![]() ,
, ![]() and
and![]() , and let
, and let![]() . Suppose that
. Suppose that ![]() satisfies the condition
satisfies the condition
![]() (2.3)
(2.3)
then
![]() (2.4)
(2.4)
Proof. If we define the function ![]() by
by
![]() (2.5)
(2.5)
then ![]() is analytic in
is analytic in![]() , with
, with ![]() and
and![]() . Making use of the logarithmic differentiation on both sides of (2.5), we have
. Making use of the logarithmic differentiation on both sides of (2.5), we have
![]() (2.6)
(2.6)
By applying the identity (1.7) in (2.6), we observe that
![]()
Hence, by using Lemma 1, we conclude that
![]()
which completes the proof of Theorem 1.
Remark 1. Putting![]() ,
, ![]() and
and ![]() in Theorem 1, we obtain the result due to Lashin ([6] , Theorem 2.2).
in Theorem 1, we obtain the result due to Lashin ([6] , Theorem 2.2).
Taking ![]() and
and ![]() in Theorem 1, we have the following corollary.
in Theorem 1, we have the following corollary.
Corollary 1. Let![]() ,
, ![]() and
and![]() . Suppose that
. Suppose that ![]() satisfies the condition
satisfies the condition
![]()
then
![]()
Theorem 2. Let![]() ,
, ![]() ,
, ![]() and
and![]() . Suppose that
. Suppose that ![]() satisfies the condition
satisfies the condition
![]() (2.7)
(2.7)
then
![]() (2.8)
(2.8)
Proof. If we set
![]() (2.9)
(2.9)
then ![]() is analytic in
is analytic in![]() , with
, with ![]() and
and![]() . By using the logarithmic differentiation on both sides of (2.9), we obtain
. By using the logarithmic differentiation on both sides of (2.9), we obtain
![]()
Thus, in view of Lemma 1, we have
![]()
which evidently proves Theorem 2.
Remark 2. Setting ![]() and
and ![]() in Theorem 2, we get the result obtained by Goyal and Goswami ([7] , Corollary 3.6).
in Theorem 2, we get the result obtained by Goyal and Goswami ([7] , Corollary 3.6).
Putting ![]() in Theorem 2, we obtain the following result.
in Theorem 2, we obtain the following result.
Corollary 2. Let![]() . Suppose that
. Suppose that ![]() satisfies the condition
satisfies the condition
![]()
then
![]()
Finally, we consider the generalized Bernardi-Libera-Livingston integral operator ![]()
![]() defined by (cf. [8] [9] and [10] )
defined by (cf. [8] [9] and [10] )
![]() (2.10)
(2.10)
Theorem 3. Let![]() ,
, ![]() ,
, ![]() and
and![]() , and let
, and let![]() . Suppose that
. Suppose that ![]() satisfies the condition
satisfies the condition
![]() (2.11)
(2.11)
then
![]() (2.12)
(2.12)
Proof. From (2.10) we observe that
![]() (2.13)
(2.13)
If we let
![]() (2.14)
(2.14)
then ![]() is analytic in
is analytic in![]() , with
, with ![]() and
and![]() . Differentiating both sides of (2.14) logarithmically, it follows that
. Differentiating both sides of (2.14) logarithmically, it follows that
![]() (2.15)
(2.15)
Hence, by applying the same arguments as in the proof of Theorem 1 with (2.13) and (2.15), we obtain
![]()
which proves Theorem 3.
Acknowledgements
This work was supported by Daegu National University of Education Research Grant in 2014.