1. Introduction
The alternative direction implicit finite difference time domain (ADI-FDTD) methods, proposed in [1] [2] , are interesting and efficient methods for numerical solutions of Maxwell equations in time domain, and cause many researchers’ work since ADI-FDTD overcomes the stability constraint of the FDTD scheme [3] . For example, it was proved by Fourier methods in [4] -[8] that the ADI-FDTD methods are unconditionally stable and have reasonable numerical dispersion error; Reference [9] studied the divergence property; Reference [10] studied ADI-FDTD in a perfectly matched medium; Reference [11] gave an efficient PML implementation for the ADI-FDTD method. By Poynting’s theorem, Energy conservation is an important property for Maxwell equations and good numerical method should conform it. In 2012, Gao [12] proposed several new energy identities of the two dimensional (2D) Maxwell equations with the perfectly electric conducting (PEC) boundary conditions and proved that ADI-FDTD is approximately energy conserved and unconditionally in the discrete L2 and H1 norms. Is there any other structure which can keep energy conservation for Maxwell equations? Is there any other energy identity for ADI-FDTD method? This two interesting questions promote us to find other energy- conservation structure.
In this paper, we focus our attention on structure with periodic boundary conditions and propose energy identities in L2 and H1 norms of the 2D Maxwell equations with periodic boundary conditions. We derive the energy identities of ADI-FDTD for the 2D Maxwell equations (2D-ADI-FDTD) with periodic boundary conditions by a new energy method. Several modified energy identities of 2D-ADI-FDTD in terms of the discrete L2 and H1 norms are presented. By these identities it is proved that 2D-ADI-FDTD with the periodic boundary conditions is unconditionally stable and approximately energy conserved under the discrete L2 and H1 norms. To test the analysis, experiments to solve a simple problem with exact solution are provided. Computational results of the energy and error in terms of the discrete L2 and H1 norms confirm the analysis on the energy conservation and the unconditional stability.
The remaining parts of the paper are organized as follows. In Section 2, energy identities of the 2D Maxwell equations with periodic conditions in L2 and H1 norms are first derived. In Section 3, several modified energy identities of the 2D-ADI-FDTD method are derived, the unconditional stability and the approximate energy conservation in the discrete L2 and H1 norms are then proved. In Section 4, the numerical experiments are presented.
2. Energy Conservation of Maxwell Equations and 2D-ADI-FDTD
Consider the two-dimensional (2D) Maxwell equations:
 (2.1)
(2.1)
in a rectangular domain with electric permittivity ε and magnetic permeability μ, where ε and μ are positive constants; 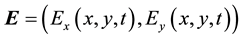 and
and 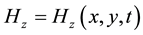 denote the electric and magnetic fields,
denote the electric and magnetic fields,  ,
, .
.
We assume that the rectangular region Ω is surrounded by periodic boundaries, so the boundary conditions can be written as
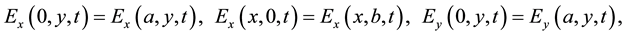 (2.2)
(2.2)
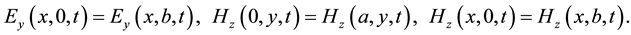 (2.3)
(2.3)
We also assume the initial conditions
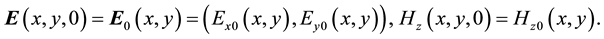 (2.4)
(2.4)
It can be derived by integration by parts and the periodic boundary conditions (2.2)-(2.3) that the above Maxwell equations have the energy identities:
Lemma 2.1 Let 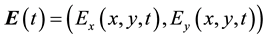 and
and 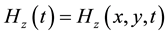 be the solution of the Maxwellsystems (2.1)-(2.4). Then
be the solution of the Maxwellsystems (2.1)-(2.4). Then
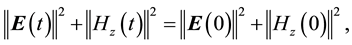 (2.5)
(2.5)
where and in what follows, 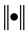 denotes the L2 norm with the weights ε (corresponding electric field) or µ (magnetic field). For example,
denotes the L2 norm with the weights ε (corresponding electric field) or µ (magnetic field). For example,
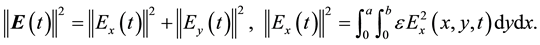 (2.6)
(2.6)
Identity (2.5) is called the Poynting Theorem and can be seen in many classical physics books. Besides the above energy identities, we found new ones below.
Theorem 2.2 Let 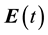 and
and 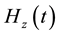 be the solution of the Maxwell systems (2.1)-(2.4), the same as those in Lemma 2.1. Then, the following energy identities hold
be the solution of the Maxwell systems (2.1)-(2.4), the same as those in Lemma 2.1. Then, the following energy identities hold
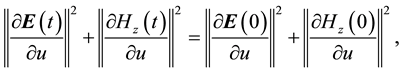 (2.7)
(2.7)
![]() (2.8)
(2.8)
where u = x or y, and ![]() is the H1 norm (the H1 norm of f is defined by
is the H1 norm (the H1 norm of f is defined by![]() , where
, where
![]() ,
, ![]() ,
,![]() .
. ![]() is also called the H1-semi norm of f).
is also called the H1-semi norm of f).
Proof. First, we prove Equation (2.7) with u = x. Differentiating each of the Equations in (2.1) with respect to x leads to
![]() (2.9)
(2.9)
By the integration by parts and the periodic boundary conditions (2.2)-(2.3), we have
![]() (2.10)
(2.10)
where
![]() (2.11)
(2.11)
Multiplying the Equations (2.9) by![]() ,
, ![]() and
and ![]() respectively, integrating both sides over
respectively, integrating both sides over ![]() and using (2.10), we have
and using (2.10), we have
![]() (2.12)
(2.12)
From (2.1) and the boundary conditions (2.2)-(2.3) we note that
![]() (2.13)
(2.13)
So,![]() . Then, by integrating (2.12) with respect to time over
. Then, by integrating (2.12) with respect to time over![]() , we get equation (2.7) with u = x. Similarly, the identity (2.7) with u = y can be proved. Combining (2.5) and (2.7) leads to (2.8).
, we get equation (2.7) with u = x. Similarly, the identity (2.7) with u = y can be proved. Combining (2.5) and (2.7) leads to (2.8). ![]()
The 2D-ADI-FDTD Scheme
The alternating direction implicit FDTD method for the 2D Maxwell equations (denoted by 2D-ADI-FDTD) was proposed by (Namiki, 1999). For convenience in analysis of this scheme, next we give some notations. Let
![]()
where Δx and Δy are the mesh sizes along x and y directions, ∆t is the time step, I, J and N are positive integers. For a grid function![]() , define
, define
![]()
where u = x, y or t. For![]() ,
, ![]() ,
, ![]() , define some discrete energy norms based on the Yee staggered grids (Yee, 1966),
, define some discrete energy norms based on the Yee staggered grids (Yee, 1966),
![]()
Other norms:![]() ,
, ![]() and
and ![]() are similarly defined. Denote by
are similarly defined. Denote by ![]() and
and ![]()
the approximations of ![]() (u = x, y) and
(u = x, y) and![]() , respectively. Then the 2D-ADI-FDTD scheme for (2.1) is written as
, respectively. Then the 2D-ADI-FDTD scheme for (2.1) is written as
Stage 1:
![]() (2.14)
(2.14)
![]() (2.15)
(2.15)
![]() (2.16)
(2.16)
Stage 2:
![]() (2.17)
(2.17)
![]() (2.18)
(2.18)
![]() (2.19)
(2.19)
For simplicity in notations, we sometimes omit the subscripts of these field values without causing any ambiguity. By the definition of cross product of vectors, the boundary conditions for (2.2)-(2.3) become
![]() (2.20)
(2.20)
where ![]() or
or![]() . Finally, the initial values
. Finally, the initial values ![]() and
and ![]() of the2D-ADI-FDTD scheme are obtained by the initial condition (2.4).
of the2D-ADI-FDTD scheme are obtained by the initial condition (2.4).
3. Modified Energy Identities and Stability of 2D-ADI-FDTD in H1 Norm
In this Section we derive modified energy identities of 2D-ADI-FDTD and prove its energy conservation and unconditional stability in the discrete H1 norm.
Theorem 3.1 Let![]() ,
, ![]() and
and ![]() be the solution of the ADI-FDTD scheme (2.14)-(2.19). Then the following modified energy identities hold,
be the solution of the ADI-FDTD scheme (2.14)-(2.19). Then the following modified energy identities hold,
![]() (3.1)
(3.1)
![]() (3.2)
(3.2)
where for![]() , and
, and ![]() or 0
or 0
![]()
Proof. First we prove (3.1). Applying ![]() to the Equations (2.14)-(2.19), and rearranging the terms by the time levels, we have
to the Equations (2.14)-(2.19), and rearranging the terms by the time levels, we have
![]() (3.3)
(3.3)
![]() (3.4)
(3.4)
![]() (3.5)
(3.5)
![]() (3.6)
(3.6)
![]() (3.7)
(3.7)
![]() (3.8)
(3.8)
Multiplying both sides of the equations, (3.3)-(3.4) by ![]() respectively, and those of (3.5) by
respectively, and those of (3.5) by![]() , and taking the square of the updated equations lead to
, and taking the square of the updated equations lead to
![]() (3.9)
(3.9)
![]() (3.10)
(3.10)
![]() (3.11)
(3.11)
Applying summation by parts, we see that
![]() (3.12)
(3.12)
where we have used that ![]() and that
and that![]() , which can be obtained from the periodic boundary conditions. Similarly, we get that
, which can be obtained from the periodic boundary conditions. Similarly, we get that
![]() (3.13)
(3.13)
So, if summing each of the Equalities (3.9)-(3.11) over their subscripts, adding the updated equations, multiplying both sides by ΔxΔy, and using the two identities, (3.12) and (3.13), together with the norms defined in Subsection 2.2, we arrive at
![]() (3.14)
(3.14)
Similar argument is applied to the second Stage (3.6)-(3.8), we have
![]() (3.15)
(3.15)
Combination of (3.14) and (3.15) leads to the identity (3.1). Identity (3.2) is similarly derived by repeating the above argument from the operated Equations (2.14)-(2.19) by![]() . This completes the proof of Theorem 3.1.
. This completes the proof of Theorem 3.1. ![]()
In the above proof, if taking ![]() as the identity operator, we obtain that
as the identity operator, we obtain that
Theorem 3.2 Let![]() ,
, ![]() and
and ![]() be the solution of 2D-ADI-FDTD. Then, the following energy identities hold
be the solution of 2D-ADI-FDTD. Then, the following energy identities hold
![]() (3.16)
(3.16)
Combining the results in Theorems 3.1 and 3.2 we have
Theorem 3.3 If the discrete H1 semi-norm and H1 norm of the solution of 2D-ADI-FDTD are denoted respectively by
![]()
then, the following energy identities for 2D-ADI-FDTD hold
![]() (3.17)
(3.17)
![]() (3.18)
(3.18)
Remark 3.4 It is easy to see that the identities in Theorems 3.1, 3.2 and 3.3converge to those in Lemma 2.1 and Theorem 2.2 as the discrete step sizes approach zero. This means that2D-ADI-FDTD is approximately energy-conserved and unconditionally stable in the modified discrete form of the L2 and H1 norms.
4. Numerical Experiments
In this section we solve a model problem by 2D-ADI-FDTD, and then test the analysis of the stability and energy conservation in Section 3 by comparing the numerical solution with the exact solution of the model. The model considered is the Maxwell equations (2.1) with![]() ,
, ![]() ,
, ![]() , and its exact so-
, and its exact so-
lution is:![]()
![]() ,
, ![]()
It is easy to compute the norms of this solution are
![]()
4.1. Simulation of the Error and Stability
To show the accuracy of 2D-ADI-FDTD, we define the errors:
![]()
where![]() ,
, ![]() ,
, ![]() are the true values of the exact solution. Denote the error and relative error in the norms defined in Section 3 by ErL2, R-ErL2, ErH1 and R-ErH1, i.e.
are the true values of the exact solution. Denote the error and relative error in the norms defined in Section 3 by ErL2, R-ErL2, ErH1 and R-ErH1, i.e.
![]()
![]()
![]()
where log is the logarithmic function.
Table 1 gives the error and relative error of the numerical solution of the model problem computed by 2D- ADI-FDTD in the norms, and the convergence rates with different time step sizes Δt = 4h, 2h and h, when Δx = Δy = h = 0.01 is fixed and T = 1. From these results we see that the convergence rate of 2D-ADI-FDTD with respect to time is approximately 2 and that 2D-ADI-FDTD is unconditionally stable (when Δt = Δx = Δy = h,
the CFL number![]() ).
).
Table 2 lists the similar results to Table 1 when Δt = 0.1h is fixed, Δx = Δy varies from 2h, h and 0.5h, and the time length T = 1. From the columns “Rate” we see that 2D-ADI-FDTD is of second order in space under the discrete L2 and H1 norm.
4.2. Simulation of the Energy Conservation of 2D-ADI-FDTD
In this subsection we check the energy conservation of 2D-ADI-FDTD by computing the modified energy norms derived in Section 3 for the solution to the scheme. Denote these modified energy norms by
![]()
![]()
![]()
In Table 3 are presented the energy norms ![]() of the solution of the 2D-ADI-FDTD scheme at the time levels n = 0, n = 1000 and n = 4000 (the third to fifth rows), and the absolute values of their difference (the last two rows), where the sizes of the spatial and time steps are Δx = Δy = 0.01, Δt = 0.04. The second row shows the four kind of energies of the exact solution computed by using the definitions of
of the solution of the 2D-ADI-FDTD scheme at the time levels n = 0, n = 1000 and n = 4000 (the third to fifth rows), and the absolute values of their difference (the last two rows), where the sizes of the spatial and time steps are Δx = Δy = 0.01, Δt = 0.04. The second row shows the four kind of energies of the exact solution computed by using the definitions of![]() . From these value we see that 2D-ADI-FDTD is approximately energy-conserved.
. From these value we see that 2D-ADI-FDTD is approximately energy-conserved.
![]()
Table 1. Error of ![]() in L2 and H1 with Δx = Δy = h and different Δt.
in L2 and H1 with Δx = Δy = h and different Δt.
![]()
Table 2. Error of ![]() in L2 and H1 with Δt = 0.1h and different spatial step sizes.
in L2 and H1 with Δt = 0.1h and different spatial step sizes.
![]()
Table 3. Energy of ![]() and its error when Δx = Δy = h = 0.01, Δt = 4h and n = 0, 1000, 4000.
and its error when Δx = Δy = h = 0.01, Δt = 4h and n = 0, 1000, 4000.
5. Conclusion
In this paper, the modified energy identities of the 2D-ADI-FDTD scheme with the periodic boundary conditions in the discrete L2 and H1 norms are established which show that this scheme is approximately energy conserved in terms of the two energy norms. By the deriving methods for the energy identities, new kind of energy identities of the Maxwell equations are proposed and proved by the new energy method. Numerical experiments are provided and confirm the analysis of 2D-ADI-FDTD.