Strong Convergence Results for Hierarchical Circularly Iterative Method about Hierarchical Circularly Optimization ()
1. Introduction
For a given nonlinear operator , the following classical variational inequality problem is formulated as finding a point
, the following classical variational inequality problem is formulated as finding a point  such that
such that

Variational inequalities were initially studied by Stampacchia [1] and ever since have been widely studied, since they cover as diverse disciplines as partial differential equations, optimal control, optimization, mathematical programming, mechanics, and finance. On the other hand, a number of mathematical programs and iterative algorithms have been developed to resolve complex real world problems.
The concept of variational inequalities plays an important role in structural analysis, mechanics and economics. Recently, the hierarchical variational inequalities and hierarchical iterative sequence problems have attached many authors’ attention (see [2-11]).
2. Preliminaries and Lemma
It is well-known that, for any , there exists a unique nearest point in
, there exists a unique nearest point in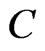 , denoted by
, denoted by , such that
, such that
 .
.
Such a mapping  from
from  onto
onto  is called the metric projection.
is called the metric projection.
Lemma 2.1 (see [12]) The metric projection  has the following basic properties:
has the following basic properties:
1)  is firmly nonexpansive, i.e.,
is firmly nonexpansive, i.e.,
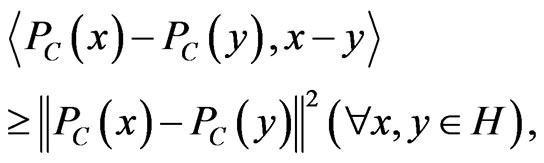
and so  is nonexpansive.
is nonexpansive.
2)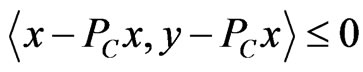 , for all
, for all  and
and .
.
Definition 2.2
1) A mapping  is said to be
is said to be  -inversestrongly monotone if there exists
-inversestrongly monotone if there exists 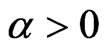 such that
such that
 .
.
2) A mapping  is said to be
is said to be 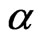 -Lipschitzian if
-Lipschitzian if
 .
.
3) A mapping  is said to be quasinonexpansive if
is said to be quasinonexpansive if  and
and
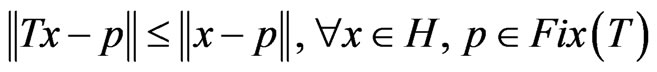 .
.
4) A mapping  is said to be strongly quasi-nonexpansive if
is said to be strongly quasi-nonexpansive if  is quasi-nonexpansive and
is quasi-nonexpansive and , whenever
, whenever  is a bounded sequence in H and
is a bounded sequence in H and  for some
for some .
.
5) (see [13]) A mapping  is said to be
is said to be  -demicontractive if
-demicontractive if  and
and
 .
.
Obviously, the above inequality is equivalent to
 and it is clear from the preceding definitions that every quasi-nonexpansive mapping is 0-demicontractive.
and it is clear from the preceding definitions that every quasi-nonexpansive mapping is 0-demicontractive.
Lemma 2.3 (see [14]) For  and
and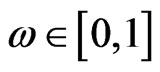 , we have the following statements:
, we have the following statements:
a) ;
;
b) ;
;

For prove our result, we give the following lemma.
Lemma 2.4 ([11]) Let  be a sequence of real numbers such that there exists a subsequence
be a sequence of real numbers such that there exists a subsequence  of
of  such that
such that  for all
for all . Then there exists a nondecreasing
. Then there exists a nondecreasing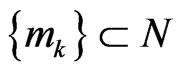 , such that
, such that 
and the following properties are satisfied for all (sufficiently large) numbers sequence :
:
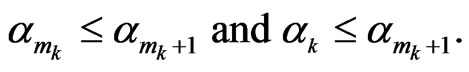
In fact,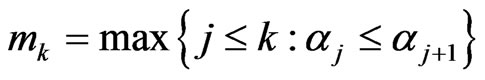 .
.
Lemma 2.5 ([11]) Assume that  is a sequence of nonnegative real numbers such that
is a sequence of nonnegative real numbers such that
 where
where  is a sequence in
is a sequence in  and
and  is a sequence such that (a)
is a sequence such that (a) ,
,  , (b)
, (b)
 . Then
. Then .
.
Lemma 2.6 ([11]) Let ,
,

and , such that
, such that
•  is a bounded sequence;
is a bounded sequence;
•  , for all
, for all ;
;
• whenever  is a subsequence of
is a subsequence of 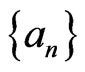 satisfying
satisfying , it follows that
, it follows that
 ;
;
•  ,
, .
.
Then .
.
In [11], the existence and uniqueness of solutions of some related hierarchical optimization problems had been discussed.
Inspired by these results in the literature, a circularly iterative method in this paper is introduced for solving a system of variational inequalities with fixed-point set constraints. Under suitable conditions, strong convergence results are proved in the setting of Hilbert spaces. Our scheme can be regarded as a more general variant of the algorithm proposed by Maingé. The results presented in the paper improve and extend the corresponding results in [11] and other.
3. Main Results
First, we discuss the existence and uniqueness of solutions of some related hierarchical optimization problems.
Theorem 3.1 Let  be quasi-nonexpansive mappings and
be quasi-nonexpansive mappings and  be contractions
be contractions . Then there exists a unique element
. Then there exists a unique element 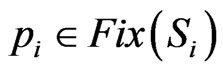 such that the following inequalities,
such that the following inequalities,
 (1)
(1)
Proof. The proof is a consequence of the well-known Banach’s contraction principle but it is given here for the sake of completeness. It is known that both sets  are closed and convex, and hence the projections
are closed and convex, and hence the projections  are well defined. It is clear that the mapping
are well defined. It is clear that the mapping

is a contraction. Hence, there exists a unique element  such that
such that
 .
.
Put  and
and
 .
.
Then ,
,  and
and .
.
Suppose that there is an element
 such that the following inequalities,
such that the following inequalities,

Then  and
and
 .
.
Hence,
 .
.
This implies that  and hence
and hence
 .
.
This completes the proof. 
For mappings , suppose
, suppose we define the iterative sequences
we define the iterative sequences  by
by
 (2)
(2)
where  satisfy
satisfy ,
, .
.
Theorem 3.2 For every , let
, let  be strongly quasi-nonexpansive mappings such that
be strongly quasi-nonexpansive mappings such that  are demiclosed at zero and let
are demiclosed at zero and let  be contractions with the coefficient
be contractions with the coefficient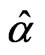 . Then the iterative sequences
. Then the iterative sequences  by (2) strong converge to
by (2) strong converge to , respectively, where
, respectively, where  is the unique element in
is the unique element in  verifying (1).
verifying (1).
Recall that a mapping 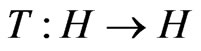 is demiclosed at zero iff
is demiclosed at zero iff  whenever
whenever  and
and .
.
We split the proof of Theorem 3.2 into the following lemmas.
Lemma 3.3 The sequences  are bounded.
are bounded.
Proof. Since  be strongly quasi-nonexpansive mappings,
be strongly quasi-nonexpansive mappings,  be contractions with the coefficient
be contractions with the coefficient . Then we have
. Then we have

Similarly, we also have

It implies that

By induction, we have

for all . In particular, sequences
. In particular, sequences 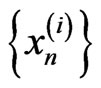 are bounded. Consequently, the sequences
are bounded. Consequently, the sequences  are also bounded.
are also bounded.
Lemma 3.4 For each , the following inequality holds:
, the following inequality holds:
 (3)
(3)
Proof. Since

Similarly, we also have

By Lemma 3.3, we give following result,
 (4)
(4)
Lemma 3.5 If there exists a subsequence  of
of  such that
such that
 then
then
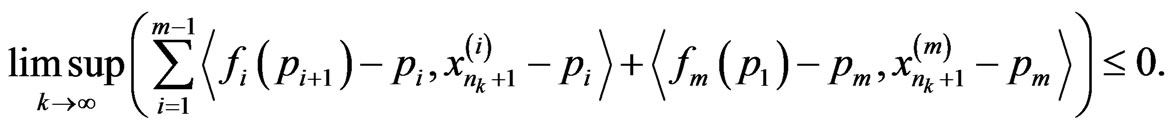 (5)
(5)
Proof. In fact, we first consider the following assertion:

By Lemma 3.3, the sequences
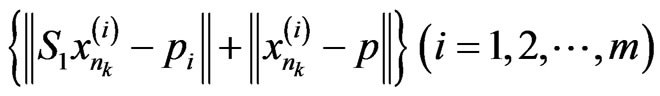
are bounded. So we have
 .
.
Since  are strongly quasi-nonexpansive,
are strongly quasi-nonexpansive,
 .
.
by the iteration scheme (1), we have
 .
.
It follows from the boundedness of  that there exists a subsequence
that there exists a subsequence  of
of  such that
such that  and
and
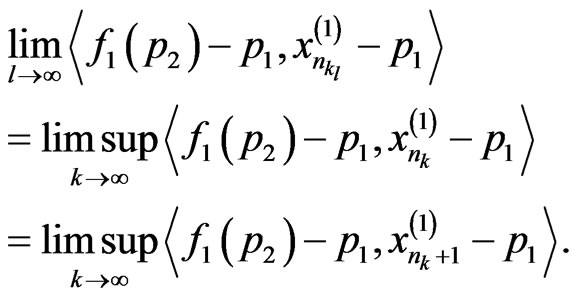
Since  is demiclosed at zero, it follows that
is demiclosed at zero, it follows that . It follows from (1), we get
. It follows from (1), we get

Consequently,
 .
.
By using the same argument, we have

Therefore, we obtain the desired inequality (4).
Next, we prove Theorem 3.2. Denote


Since

We have the following statements from Lemma (3.3), Lemma(3.4) and Lemma(3.5):
•  is a bounded sequence;
is a bounded sequence;
•  , for all
, for all ;
;
• whenever  is a subsequence of
is a subsequence of  satisfying
satisfying , it follows that
, it follows that .
.
Hence, it follows from Lemma 2.6 that , It implies that
, It implies that
 .
.
This means that
 .
.
The proof of Theorem 3.2 is completed.