Optimal Economic Life Interval Evaluation Method of Transformers ()
1. Introduction
Power enterprises are equipment-extensive, where 80% - 90% of total assets are physical equipment assets, so utilizing efficiency of main equipment directly affects overall benefit of power enterprises. Foreign experience shows equipment management based on Life cycle cost (LCC) theory can effectively improve comprehensive interests of power enterprises [1]. LCC means total expense of equipment over its entire life cycle, its total cost mainly depends on operating years of equipment, so research on economic life of equipment is of great significance for power enterprises to carry out scientific and rational LCC management.
So far, there are a lot of researches on LCC [2] [3]. Paper [4] proposes a LCC model of transformers in medium- and low-voltage distribution network. Reference [5] shows a 3-dimension LCC model for power system, which provides an idea for applying LCC to manage the whole network. For failure rate prediction, an optimization approach of Weibull model solution is proposed in [6]. An improvement of state failure rate model for power transmission and transforming equipment is presented in [7], which considers model parameters changing with time. Paper [8] proposes a method to predict economic life of power equipment which takes the maximization of annual average net income as optimization objective. But the maximization of annual average net income in the method is much subjective and the maintenance and failure cost are failed to consider the impact of failure rate. Paper [9] puts forward a method of economic life from economic operation of transformer in service, but the method ignores the LCC of transformers.
Based on the above, this paper puts forward an optimal economic life interval evaluation method of transformers based on fitted failure rate curve and minimal average annual cost of life cycle. First, the failure rate curve of transformers is fitted using historical data of transformer failure rate. Then, the operation and fault cost of life cycle are calculated through the failure rate curve. Finally, the optimal economic life interval of transformers is evaluated on the basis of the minimal average annual cost of life cycle, which uses the theory of interval analysis.
2. Introduction to Economic Life of Transformer
Generally, transformer life can be divided into technical life, physical life and economic life and other forms [10].
2.1. Economic Life of Transformer
Physical life of transformer generally refers to the life determined by the physical wear and tear, which is also the life of the transformer from the time put into service until retired due to physical wear and tear. Physical life of transformer is mainly determined by tangible wear also related to self-quality status, the use of technology and maintenance quality. But, technical life of transformer commonly means that with the development of science and technology, existing transformer will be replaced by more advanced transformer before its physical or economic life is ended. Therefore, technical life of transformer mainly indicates the time from transformer investment to its loss of use value due to technological progress. Because of the impact by the intangible wear, technical life of transformer is generally shorter than the natural life. Based on the above, transformer physical life and technical life are defined from the use of the transformer itself.
Economic life of transformer generally refers to the life determined by operation and maintenance costs of transformer. Because of transformer worn out in its late use, operation and maintenance costs of transformer is increasing. Under that circumstances, there will have a service cycle which is economic life of transformer when the average running cost is below a certain limit. Economic life is often used to analyze and determine the best life and the best update time of the transformer [11]. Therefore, we can determine the best life and the best update time of the transformer when the economic life is certain. Based on the above, there will be a year that the average running cost is minimum and the year can be considered the economic life of transformer.
2.2. Life Cycle Model of Transformer
According to the investment structure of transformer in the actual operation of power enterprises, the cost of transformer based on life cycle theory contains initial investment cost, operation cost, maintenance cost, fault cost and equipment residual value. The life cycle cost of transformer can also be divided into variable cost (including maintenance cost, fault cost) that vary with the failure rate and fixed cost (including initial investment cost, operating cost and equipment residual value) that do not vary with the failure rate.
1) Initial investment cost
The initial investment cost includes all cost before the transformer is utilized, mainly including purchase, mounting cost, test cost and so on.
 (1)
(1)
where  is purchase cost,
is purchase cost, 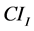 is installation and mounting cost.
is installation and mounting cost.
2) Operation cost
The operation cost mainly consists of the loss of transformer in operating.
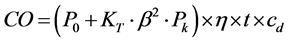 (2)
(2)
where 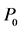 is the equivalent no-load loss,
is the equivalent no-load loss, 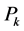 is the equivalent load loss,
is the equivalent load loss, 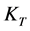 is load fluctuation loss factor,
is load fluctuation loss factor, 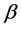 is the load factor which means the transformer loading over its time,
is the load factor which means the transformer loading over its time,  is run time,
is run time, 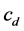 is the purchasing cost of electricity,
is the purchasing cost of electricity, 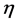 is the loss rate of load per year,
is the loss rate of load per year,
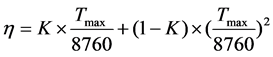 (3)
(3)
where  is the empirical coefficient,
is the empirical coefficient,  represents the number of hours in maximum load per year.
represents the number of hours in maximum load per year.
3) Maintenance cost and fault cost
Maintenance cost and fault cost vary with the failure rate. Therefore, different transformer failure time cause different economic losses. In order to quantify the economic loss of the transformer, this paper classifies transformer failures into general, severe, and catastrophic failures [12].
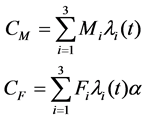 (4)
(4)
where  is maintenance cost,
is maintenance cost,  is fault cost,
is fault cost,  refers to general, severe, and catastrophic failures,
refers to general, severe, and catastrophic failures, ![]() is type
is type ![]() failure of transformer,
failure of transformer, ![]() is the maintenance cost caused by type
is the maintenance cost caused by type ![]() failure,
failure, ![]() is the comprehensive loss caused by type
is the comprehensive loss caused by type ![]() failure,
failure, ![]() is a correcting parameters.
is a correcting parameters.
4) equipment residual value
Equipment residual value refers to the residual value of recycling when the equipment retired.
![]() (5)
(5)
where ![]() is equipment residual value,
is equipment residual value, ![]() is constant coefficient for Simplified representation.
is constant coefficient for Simplified representation.
3. Transformer Failure Rate Model
3.1. Three-Parameters Weibull Distribution
In general, the Weibull distribution can be used to describe the failure rate of electrical equipment with time. Equipment cumulative failure probability ![]() refers to probability of failure in the specified conditions and time, also known as unreliable function or life distribution function in the failure rate model [13].
refers to probability of failure in the specified conditions and time, also known as unreliable function or life distribution function in the failure rate model [13].
![]() (6)
(6)
where ![]() is reliable function.
is reliable function.
Therefore, assume that the service life of electrical equipment distribution in line with the three-parameters Weibull distribution of cumulative failure probability function:
![]() (7)
(7)
where ![]() is form parameter,
is form parameter, ![]() ,
, ![]() is scale parameter,
is scale parameter, ![]() ,
, ![]() is location parameter,
is location parameter, ![]() and equipment will not usually fail before
and equipment will not usually fail before![]() ,
, ![]() refers to the operating time of equipment.
refers to the operating time of equipment.
The failure rate of equipment in the life cycle can be defined as the failure rate per hour after time ![]() when equipment has not failed.
when equipment has not failed.
![]() (8)
(8)
where ![]() is the failure rate of equipment in the life cycle.
is the failure rate of equipment in the life cycle.
Usually in the process of equipment operation, its failure rate goes through the following three stages: early failure rate of the characteristics is decreasing, known as practiced period; the middle of the failure rate is almost constant, known as using period; lately failure rate of the characteristics is increasing, known as wear-out period. As the Figure 1 shows:
The curve above can be well fitted by the Weibull distribution. The failure rate function can be described as:
![]() (9)
(9)
![]()
Figure 1. Variation of failure rate in total life process.
where three stages of the curve respectively correspond to the form parameter 0 < m < 1, m = 1, m > 1 three situations.
The failure rate curve can be fitted piecewise through the analysis of the history statistics from the same type electrical equipment based on the Weibull distribution. Then, form parameter![]() , scale parameter
, scale parameter![]() , location parameter
, location parameter ![]() can be estimated according to the fitted curve. Finally, the failure rate function is determined.
can be estimated according to the fitted curve. Finally, the failure rate function is determined.
3.2. Model Parameters Estimated
Frist, assuming that location parameter ![]() is known, form parameter
is known, form parameter ![]() and scale parameter
and scale parameter ![]() can be estimated by Levenberg―Marquardt algorithm. Then, location parameter
can be estimated by Levenberg―Marquardt algorithm. Then, location parameter ![]() is determined by the nonlinear fitting method. Specific steps are as follows:
is determined by the nonlinear fitting method. Specific steps are as follows:
1) Assuming ![]() is known as
is known as![]() , according to the failure rate function:
, according to the failure rate function:
![]() (10)
(10)
![]() (11)
(11)
2) Based on the initial value of the parameters![]() ,
, ![]() obtained by the above formula, two data points located on the Weibull distribution are selected to construct the equations:
obtained by the above formula, two data points located on the Weibull distribution are selected to construct the equations:
![]() (12)
(12)
3) According to initial value of the parameters![]() ,
, ![]() ,
, ![]() and N sets of data, we can use Matlab for iterative calculation based on Levenberg-Mar- quardt algorithm.
and N sets of data, we can use Matlab for iterative calculation based on Levenberg-Mar- quardt algorithm.
4) Parameter and scale parameter can be determined form the calculation in step3.
5)![]() , which is the cut-off point of the failure rate stages, can be calculated by the part of n sets of data based on non-linear fitting,
, which is the cut-off point of the failure rate stages, can be calculated by the part of n sets of data based on non-linear fitting,
6) The failure rate interval can be determined by the fitted curve and error ![]() which are calculated based on Matlab:
which are calculated based on Matlab:
![]() (13)
(13)
where ![]() refers to the prediction of equipment failure rate on year
refers to the prediction of equipment failure rate on year![]() .
.
4. Optimal Economic Life Interval
According to the theory of LCC, initial investment cost belongs to present value but operation cost, maintenance cost, fault cost, equipment residual value do not. Therefore, operation cost, maintenance cost, fault cost and equipment residual value need to calculate their discounted value. Assuming that transformer operate to the nth year of retirement or transformation, we can calculate the total life cycle of transformer based on the life cycle model of transformer [14]:
![]() (14)
(14)
where ![]() is the depreciation rate, t is the operating year.
is the depreciation rate, t is the operating year.
The annual average cost of LCC:
![]() (15)
(15)
As a single value of various costs tend to cause greater error, so the theory of interval analysis has been used to calculate the cost intervals. First, we can calculate the intervals of each transformers parameter. Then, all kinds of cost interval can be calculated. Finally, the optimal economic life interval of transformer can be determined when the annual average cost is the minimum.
5. Case Study
This paper takes transformer SFPSZ-120000/220 in Southern China as example to evaluate its optimal economic life interval based on the method presented above.
5.1. Failure Rate Interval
The historical data of transformer SFPSZ-120000/220 can be found in reference [15]. From the Figure 2, the demarcation point between using period and wear-out period is about 12 years.
Frist, the location parameter of Weibull contribution can be assumed as 12, ![]() , which means the transformer goes into wear-out period on 12 years. Next, the failure rate of transformer can be fitted based on Levenberg-Marquardt algorithm in order to get form parameter
, which means the transformer goes into wear-out period on 12 years. Next, the failure rate of transformer can be fitted based on Levenberg-Marquardt algorithm in order to get form parameter![]() , scale parameter
, scale parameter ![]() . Then, location parameter can be determined as
. Then, location parameter can be determined as ![]() based on nonlinear Fitting. Finally, the failure rate curve can be fitted as Figure 3. The failure rate function can be described as:
based on nonlinear Fitting. Finally, the failure rate curve can be fitted as Figure 3. The failure rate function can be described as:
![]()
Figure 2. Distribution curve of transformers failure rate.
![]()
Figure 3. Fitting curve of transformers failure rate.
![]() (16)
(16)
The failure rate can be interval:
![]() (17)
(17)
The upper and lower limit of failure rate is represented in Figure 3.
5.2. Calculation of Optimal Economic Life Interval
The annual average cost intervals of transformer can be calculated based on the failure rate fitted above. Life cycle parameter of transformer is presented as Table 1:
According to the data in the table and the failure rate calculated above, the upper and lower limits of the average annual cost in different operating years is presented in Figure 4:
In Figure 4, the annual average cost of LCC reaches a minimum of 2519.802 thousand ¥ in 33 years when the parameters of the transformer take the upper
![]()
Table 1. Parameters of transformers cost.
![]()
Figure 4. Annual average life cycle cost curve of transformers.
limit; the annual average cost of LCC reaches a minimum of 2438.77 thousand ¥ in 31 years when the parameters of the transformer take the lower limit. Therefore, the optimal economic life interval of transformer is 31 - 33 years. When the transformer reaches the optimal economic life interval between 31 to 33 years, the power enterprise can consider the overall transformer repair or replacement.
6. Conclusions
This paper proposed a method of optimal economic life interval evaluation of transformer based on failure rate curve fitted and annual average cost of LCC, thus providing scientific support for the operation and retirement strategy of electricity equipment. The method includes the following features:
1) Compared with the two-parameter Weibull distribution, the three-para- meters Weibull distribution is more accurate for fitted failure rate curve of equipment. Levenberg-Marquardt algorithm is used to estimate parameters, which can make the calculation results more accurate. The failure rate can be estimated by failure rate function, thus providing scientific support for maintenance strategy of electricity equipment.
2) The annual average cost of LCC and the cost intervals is calculated based on the LCC of transformer. The optimal economic life interval of transformer is estimated on the basis of the life cycle minimal average annual cost. The uncertainty of information is considered and the calculation error of single cost is eliminated. Therefore, the method has higher rationality and credibility.
It should be specially emphasized that this paper does not consider the impact of maintenance and environmental on the failure rate, which is due to lack of actual maintenance data and operating environment conditions. If there is more access to environmental and maintenance data, we can conduct a detailed study of the impact of maintenance and environmental on the failure rate.
Acknowledgements
This paper was partially supported by Science and technology project in Hubei Electric Power Co. Ltd “Under the new situation in Hubei province energy conservation, loss reduction strategy and key technology research”.