History of Krylov-Bogoliubov-Mitropolsky Methods of Nonlinear Oscillations ()
1. Introduction
When physicists or engineers are faced with a theoretical investigation of a real physical system, they are always forced to simplify and to idealize the problem in order to represent its time properties. Consequently, the idealization of the problem can never be avoided in the construction of a mathematical model which is a set of equations, normally a set of differential equations representing the dynamic behavior of the system (Nayfeh & Balachandran, 1995; Nayfeh & Mook, 1979) . In this mathematical model all the main features of the problem must appear, but it is neither necessary nor feasible to include all the properties of the system because of the difficulties involved in resolving it, if indeed this is actually possible. Since idealization is inevitable, the question is how to go far in the direction of idealization to obtain satisfactory results? The answer to this question is only given by experimental results, which may or may not legitimate the idealization made.
In nonlinear problems new phenomena arise, which is not the case of linear systems. Thus, in the study of nonlinear problems the main objective is to understand these new characteristics of the system and to improve the accuracy of linear methods. Due to the complexity of the phenomena, one practical approach is to settle for something less than complete generality (Dumas, Meyer, & Schmidt, 1995; Katok & Hasselblatt, 1995) . Hence, it is preferable to study solutions for nonlinear problems and look for nonlinear solutions close to a known linear solution. This is the basic idea behind the use of perturbation methods for nonlinear problems (Nayfeh, 1973) . It consists of developing the method in relation to a small parameter, in which a series expansion in terms of this parameter can be found. The coefficients of the expansions are obtained as solutions of a sequence of linear problems.
The Krylov-Bogoliubov school in Kiev developed analytical methods for nonlinear systems. The foundation of their results was the classical perturbation method which was generalized to non-conservative systems. In the 1950s, the invention of the high-speed computer changed the history of dynamics. It allowed the simulation of dynamical systems with complicated equations in a way that was previously impossible, and was therefore a significant development of intuition about nonlinear systems. Such simulations led to Lorentz’s discovery in 1963 of chaotic motion in a strange attractor. He studied a simplified model of convection rolls in the atmosphere to gain insight into the unpredictability of weather. Lorentz found that the solutions of these equations never settled down to an equilibrium or periodic state. Instead they continued to oscillate in an irregular aperiodic fashion. He also noticed that the resulting behaviors from two slightly different initial conditions would soon become completely different. The surprising implication was that the system was inherently unpredictable. In other words, chaotic characteristics can appear in deterministic mathematical models.
2. Main Developments of Nonlinear Theories before 1930
The main contributions to nonlinear methods before K-B-M are as follows:
Before 1880 (The analytic period): characterized by the search for analytic solutions and perturbation methods; the search for integrals of motion, particularly independent time and algebraic integrals.
Main areas: classical mechanics, celestial mechanics―Newton, Euler, Lagrange, Laplace, Jacobi, etc. Hydrodynamics―Rayleigh, who briefly considered limit cycles and the bifurcation concept. Kinetic theory of gases-the Boltzman equation: the H-function, statistical concept of entropy.
1879-1900 (Sophus Lie): (similarity transformations); a general principle for obtaining integrals of nonlinear partial differential equations by determining invariance properties in a continuous group (Lie group); a frequent application is invariance with some scaling.
Bruns (1887): the only independent algebraic integrals for the motion of the three-body problem (which has 18 integrals) are the ten ‘classic integrals’ (energy, total linear momentum, total angular momentum, and time-dependent equations for the motion of the center of mass).
Painlevé (1898): the only independent integrals of the motion of the N-body problem, which involve velocities algebraically (regardless how the spatial coordinates enter) are the classic integrals.
Stability of motion-A. M. Lyapunov’s results (1892); Lyapunov exponent.
Korteweg and de Vries demonstrated the existence of finite amplitude solitary water waves.
Poincaré (1880-1910): emphasized the study of the qualitative, global aspects of dynamics in phase space; developed topological analysis; generalized the bifurcation concept: introduced mapping in phase space (difference equations); surface of section; introduced rotation numbers of maps; index of a closed curve in a vector field; initiated the recursive method for defining dimensions.
Whittaker: obtained the adelphic integrals for coupled harmonic oscillators, where the integrals are never analytic functions of frequencies (1906).
1920-1930
Numerical computations by Stormer and his students, of the dynamics of solar particles in the dipole magnetic field of the earth (a non-integrable system), from 1907-30.
The Mandelstam-Andronov school of applied nonlinear analysis; replacement of a nonlinear system by a set of linear segments.
Enrico Fermi (1923): attempted to generalize Poincaré’s theorem to prove ergodicity in some systems.
Van der Pol: the extensive study of limit cycles, relaxation oscillations, leading to singular perturbation theory; studied the forced van der Pol oscillator with van der Mark (1927); observed subharmonic generation, hysteresis, ‘noisy’ regions in parameter space. A variety of bifurcation phenomena.
The Andronov-Poincaré bifurcation (1930).
Krylov-Bogoliubov-Mitropolski: further refined the averaging method of perturbation theory.
3. Poincaré’s Pioneering Work
The father of modern nonlinear dynamics is Henri Poincaré (1854-1912). Previous studies of dynamics in the 1880s included analytical solutions of dynamic equations, astronomical investigations of planetary motions, and Lord Rayleigh’s (1842-1919) studies of dynamical systems. Important names in mathematics are associated with these studies, such as Newton (1642-1726), Leibniz (1646-1716), Euler (1707-1783), Gauss (1777-1835), Lagrange (1736-1813), Laplace (1749-1827), Jacobi (1804-1851), Lie (1842-1899), and, of course Poincaré, amongst others. One of the big problems at that time was the three-body problem (Green, 1997; Valtonen & Karttunen, 2006) .
It was Poincaré who provided many of the solutions now used as established methods for exploring dynamic systems. In particular, he emphasized the importance of obtaining a global qualitative understanding of the nature of a dynamic system. Many of his suggestions were substantially refined and extended by others, but our debt to his insights is enormous. Unfortunately, his contributions in this field were ignored by scientists for about 50 years. Fortunately, not by many mathematicians, who extended his concepts and theories to areas such as topology, asymptotic series, various maps and their fixed points, bifurcations and also proved a number of his conjectures.
We can summarize the contributions of Poincaré for dynamic systems as follows:
The qualitative theory of differential equations
The study of global stability of sets of trajectories, instead of focusing on single solutions
The notion of bifurcation together with the study of dynamical families depending on a parameter
The introduction of probabilistic concepts into dynamics, with respect to ergodic theory and the exclusion of exceptional cases.
Poincaré studied in two famous schools: École Polytechnique and École des Mines, entering the former in 1873 (Verhulst, 2012) . His professors of science at the Polytechnique were Charles Hermite (Analysis), Marie-Alfred Cornu (Physics), Louis Jean Résel (Mechanics), Amédée Manheim (Geometry), Hervé Faye (astronomy) and Edmond Fremy (Chemistry). Furthermore, his two most influential professors were Hermite and Cornu.
Poincaré was immersed in the Polytechnic School’s great tradition in mathematical analysis. It is worth emphasizing that the first lecturer of this discipline was Lagrange. However, the teaching of mathematics in that school had deeper roots. Historically it belonged to a tradition that began in the Renaissance of being part of the army career, as well as being of fundamental importance for the education of nobles. From 1750 onwards, mathematicians such as Huygens (1629-1695), Bernoullis, Euler, Monge (1746-1818), etc., joined in France the so-called ‘scientist-engineers,’ like Borda (1733-1799) and Coulomb (1736-1806), who were also members of the Academy of Sciences.
4. Science and the Russian Revolution
The 1917 Bolshevik Revolution resulted in radical changes throughout
Russia
, which affected the development of science. The Revolution and the ensuing civil war had serious consequences for the lives and work of scientists of the pre-revolutionary generation (Graham, 1993) .
“In the few months of 1917 where the liberals and the democratic socialists were in power, reforms were made which influenced the future of Soviet science. Universities adopted new structures of faculty governance; professional societies affirmed their independence from state control and the
Academy
of
Sciences
, for the first time in its history, elected its own president, the geologist A. P. Karpinskii. The permanent secretary of the Academy, S. F. Oldenburg, was also Minister of Education in the provisional government” (Graham, 1993) .
“One paradoxical situation that appears in early Soviet Russia is that the scientific institutions normally aligned with the conservative forces, such as the Academy of Sciences, were less resistant to the Bolshevik Revolution than the universities and other scientific institutions” (Graham, 1993) . This situation can be interpreted as due to the prevailing wish of leading scientific researchers to keep politics separate from science. The principle of keeping science out of politics was strong in the Central European universities where many Russian scholars had studied and was frequently expressed by the old researchers.
Although leaders of the Academy adopted defensive measures, the revolutionaries began to formulate plans for a reorganization of science. In these plans the idea of diminishing the role of the Academy was present. Probably the most ambitious plan to reorganize Russian science came from the Commissariat of Education, based mainly among the northern communes, including Petrograd. The basic purpose of this project was to “win science for the proletariat”, and to fight against the “fetishization of pure science”, according to them endemic in the traditional institutions.
The northern radicals wanted to abolish the Academy of Sciences and all “old forms of the social organization of science”. They intend to replace the Academy with a “homogeneous set of scholarly-pedagogical institutes” where teaching was to be the primary function (Pollock, 1969) . Here we cannot resist a comparison with a similar situation in France. During the French Revolution, the National Convention suppressed all royal academies, including the French Academy in 1792. They were all replaced in 1795 by a single institution, called Institut de France.
The institutions that had traditionally been involved only with theoretical research would be required to assume major pedagogical responsibilities. Obviously, behind this proposal there was a strategic idea of constructing the “unity of scholarly and teaching work”.
In the 1930s, after the Bolsheviks had abandoned their original ideal of an international communistic revolution and had begun to build a communist state at home (in a single country only), overall scientific activity increased. The doctrine of Marxism-Leninism (White, 1996) , the ideology of Soviet orthodoxy, began to create a “scientific” theory for the development of society.
Naturally, this meant that official Marxist ideology was adapted to the party’s immediate needs party and immediately came to dominate the social sciences and the sciences in general, just when a new period of development was arising (Cohen, 1978) .
5. The Intellectual Context of the Soviet Union
Like the October Revolution, World War II deeply affected intellectual life in U.S.S.R (Montefiore, 2005) .
At the beginning of World War II, the
Soviet Union
signed a non-aggression pact with Nazi Germany, initially avoiding confrontation. As is well know, this treaty was disregarded in 1941 when the Nazis invaded Soviet Union, opening the largest and bloodiest theatre of combat in the history of mankind. The battles were intense and became famous in military history, such as Stalingrad.
Following the German attack on 22 June 1941, most of the Institutes and Universities from the west of
Russia
were evacuated into eastern regions far from the battle lines. Nikolay Bogoliubov moved to Ufa, the capital of the Republic of Bashkortostan, where he became Head of the Department of Mathematical Analysis at UFA State Aviation Technical University, from July 1941 to August 1943. In autumn 1943, he was evacuated to Moscow, where on 1 November 1943 he accepted a position in the Department of Theoretical Physics of the Moscow State University. At that time the Head of the Department was Anatoly Vlasov. Theoretical physicists working in the Department in that period included Dmitry Ivanenko, Arsenij Sokolov, and other very famous scientists.
Like Bogoliubov, Mitropolsky’s career was also significantly influenced by World War II. He graduated from Kazakh University in 1942 after studying there for six months. After graduating he attended the Ryazan Military Artillery
School
, from where in 1943 he was sent to the front, where he commanded an artillery intelligence platoon until the end of the war. In 1946, he was demobilized and began his research at the Institute of
Constructive Mechanics
of the Ukrainian Academy of Sciences under the supervision of Nikolai Bogoliubov.
In the 1943-46 period, Bogoliubov’s research was essentially concerned with the theory of stochastic processes and asymptotic methods. In 1945, he proved a fundamental theorem about the existence and basic properties of a one-parameter integral manifold for a system of nonlinear differential equations. He also investigated periodic and quasi-periodic solutions lying on a one-dimensional manifold, thereby establishing the foundation for a new method of nonlinear mechanics, the method of integral manifolds.
In 1946, he was elected as a corresponding member of the
Academy
of
Sciences
of the USSR. In 1947, he organized and became the Head of the Department of Theoretical Physics at the Steklov Mathematical Institute. While working in the Institute, Bogoliubov and his school contributed to science with many important works on renormalization theory and on the theory of dispersion relations.
On 26 January 1953, Bogoliubov became the Head of the Department of Theoretical Physics at Moscow State University, after Anatoly Vlasov decided to leave the position on 2 January 1953. He was elected a full member and academician of the Academy of Sciences of the Ukranian SSR and a full member of the Academy of Sciences of the USSR in the same year.
In March 1953 Josef Stalin died and immediately a progressive but general liberation of the regime began. A new era for cultural and scientific work was also commencing.
6. KBM Biographical Note
Krylov is a well-known mathematician, making his contributions in several fields of this discipline, such as interpolation, nonlinear mechanics and numerical methods for solving equations of mathematical physics. He graduated from the St. Petersburg State Mining Institute in 1902. Between 1912 and 1917 he held the position of professor in this Institute. In 1917 he moved to Crimea to become professor at the Crimea University. He worked there until 1922 and then moved to
Kiev
to become chairman of the Mathematical Physics Department at the Ukrainian Academy of Sciences.
Krylov (Figure 1) developed methods for the analysis of mathematical physics, which can be used not only to prove the existence of solutions but also their construction. In 1932 he began to work with his student Nikolay Bogoliubov on mathematical problems of nonlinear mechanics. In this period they invented asymptotic methods for the integration of nonlinear differential equations, studied dynamical systems, and made significant contributions to the foundation of nonlinear mechanics. They proved the first theorems about the existence of invariant measures known as the Krylov-Bogoliubov theorems, introduced the Krylov-Bogoliubov averaging methods and, together with Yuri Mitropolski, asymptotic methods for approximate solving equations of nonlinear mechanics.
Bogoliubov (Figure 2) a Russian mathematician and theoretical physicist, is famous for his significant contribution to quantum field theory, classical and quantum statistical mechanics, and to the theory of dynamical systems. He was born in Nizhny Novgorod, moving to Kiev with his family in 1921 soon after he began to study physics and mathematics.
![]()
Figure 1. Nikolay Mitrofanovitch Krylov (1879-1955).
![]()
Figure 2. Nikolay Nikolayevitcch Bogoliubov (1909-1992).
At this time he attended research seminars in Kiev University and soon started to work under the supervision of Nikolay Krylov. In 1924, at the age of 15, Bogoliubov wrote his first scientific paper: On the Behaviour of Solutions of Linear Differential Equations at Infinity. In 1925 he entered a PhD program at the Academy of Sciences in Ukraine and obtained an equivalent title to PhD in 1928, at the age of 19, with a thesis entitled: On Direct Methods of Variational Calculus. In 1930 he obtained the degree of Doctor of Sciences, the highest title in the Soviet Union, for which a significant independent contribution to his scientific field had to have been made.
In 1931, Krylov and Bogoliubov began to work together on the problems of nonlinear oscillations. They were the key figures in the ‘Kiev School of Nonlinear Oscillation Research,’ with a fruitful cooperation beginning with the paper: On the Quasiperiodic Solutions of the Equations of Nonlinear Mechanics (1934) and the book Introduction to Nonlinear Mechanics (1937). These works created a large field of nonlinear mechanics.
Mitropolsky was a renowned Ukrainian Soviet mathematician known for his contributions to the fields of dynamical systems and nonlinear oscillations. He was born in Poltava Governorate and died in Kiev. He received his PhD from Kiev State University in 1948, under the supervision of the mathematician Nikolay Bogoliubov. He studied the problem of resonant phenomena in nonlinear oscillatory systems with slowly varying parameters. The approach he used was the Krylov-Bogoliubov asymptotic method. In 1951, he presented another thesis, equivalent to the habilitation, with the title: Slow processes in nonlinear oscillatory systems with many degrees of freedom.
In 1958, he became Director of the Mathematics Institute in Kiev, and a member of the Mathematics Department of the Ukrainian Academy of Sciences, also becoming an Academician of the Ukrainian Academy in 1961. In 1966 he became Academic Secretary of the Mathematics and Cybernetics Department of the Ukrainian Academy of Sciences and Academician of the Mathematics Department of the National Academy of the SSSR.
He was awarded the following prizes: State Prize for Science and Technology in 1980 and the V. I. Vernadskii Prize for Geology, Geochemistry, and Hydrophysics in 1985. In 1986, he received the A. M. Liapunov Gold Medal for his scientific contributions to Russian sciences.
Anatoly Samoilenko, who published some papers with Mitropolsky, was a student awarded his PhD with Mitropolsky in 1963, as well as working on many mathematical projects with him. When Mitropolsky retired in 1988, Samoilenko took over the direction of the Institute of Mathematics.
Mitropolsky (Figure 3) also authored the following books: Nonstationary process in nonlinear oscillatory systems (1955), Problems in the asymptotic theory of nonstationary oscillations (1964), Lectures on the method of averaging in nonlinear mechanics (1966), The method of averaging in nonlinear mechanics (1971), Nonlinear mechanics. Asymptotic methods (1995), Nonlinear mechanics. Monofrequency oscillations (1997) and Methods of nonlinear mechanics. A first textbook (2005).
7. Common Selected Works and Books
N. M. Krylov and N. N. Bogoliubov (1934): On Various Formal Expansions of Nonlinear Mechanics, Kiev, Izdat, (Ukrainian).
N. M. Krylov and N. N. Bogoliubov (1947): Introduction to Nonlinear Mechanics, Princeton, Princeton University Press.
N. N. Bogoliubov and Y. A. Mitropolski (1961): Asymptotic Methods in the Theory of Nonlinear Oscillations, New York, Gordon and Breach.
N. N., Bogoliubov and B. I. Sadovnokov (1963): On the Periodic Solutions of a Differential Equation of Order n with a Small Parameter, in Proceedings of the International Symposium on Nonlinear Oscillations, Izd-voAkad. NaukUkSSR, Kiev, 155-165.
N. N. Bogoliubov (1964): On the Quasiperiodic Solutions in the Problems of Nonlinear Mechanics, in Proceedings of the First Mathematical Summer School, Pt. I., Kiev, 11-101.
N. N. Bogoliubov and Y. A. Mitropolsky (1965): On the Investigation of Quasiperiodic Modes in Nonlinear Oscillatory Systems, Colloq. International. Centre Nat. Rech. Scient., No. 148, 181-192.
Y. A. Mitropolsky and O. B. Lykova (1965): Behavior of Solutions of Nonlinear Equations in the Vicinity of the Equilibrium Position, in Matema. Fizika, Naukova Dumka, Kiev, 74-96.
Y. A. Mitropolsky and Samoilenko A. M (1972): Conditionally Periodic Oscillations in Nonlinear Systems, in Matem. Fizika, no.12, 86-105.
Y. A. Mitropolsky and A. K. Lopatin (1973): On the Reduction of Systems of Nonlinear Differential Equations to Normal Form, in Matem. Fizika, Naukova Dumka, Kiev, No. 14, 125-140.
Y. A. Mitropolsky and Samoilenko A. M (1973): Multifrequency Oscillations in Nonlinear Systems, in Nonlinear Vibration Problems, Zagadnieniadrgannielinlowych, PWN, Warsawa, 14, 27-38.
![]()
Figure 3. Yurii Alexeevitch Mitropolsky (1917-2008).
Y. A. Mitropolsky and Samoilenko A. M (1977): Some Problems in Multifrequency Oscillations, Abh. DAW, Abt. Math. Naturwiss, Techn., Heft 4, 107-116.
Y. A. Mitropolsky and A. A. Martynyuk (1978): On Some Lines of Research Concerning the Stability of Periodic Motions and the Theory of Nonlinear Oscillations, Prikladnaya Mekanika, Izd-voAkad. NaukUkSSR, 14, no. 3, 3-13.
8. Some of Mitropolsky’s Additional Contributions
Mitropolsky made some fundamental contributions to the theory of nonlinear mechanics, especially the qualitative theory of differential equations, as well as the development of asymptotic methods applied to the solution of practical problems (Mitropolsky, 1963) . He extended the Krylov-Bogoliubov symbolic method to nonlinear systems and generalized asymptotic methods to the theory of nonlinear mechanics. Using methods of successive substitutes, he constructed a general solution for a system represented by a nonlinear equation and studied its behavior in the neighborhood of the quasi-periodic solution. He also successfully applied the averaging method to the study of oscillatory systems with slowly varying parameters (Mitropolsky, 1970) .
We can list the majority of Mitropolsky’s contributions as follows:
The creation and the development of the mathematical justification of algorithms for the construction of asymptotic expansions for nonlinear differential equations describing non-stationary oscillatory processes.
The development of a method for investigation of monofrequency processes in oscillatory systems.
The investigation of systems of nonlinear differential equations, describing oscillatory processes in gyroscope systems and strongly nonlinear systems.
The development of the theory of integral manifolds in nonlinear mechanics and the consideration of related questions that arise in stability of motion.
The development of the averaging method for equations with slowly varying parameters, as well as for equations with non-differentiable and discontinuous right-hand sides for equations with delayed argument, for equations with random perturbations, and for partial differential equations and equations in functional spaces.
The development of the method of accelerated convergence in problems of nonlinear mechanics.
The development of the theory of reducibility in linear differential equations with quasi-periodic coefficients and other equations.
In 1955, Mitropolsky and Bogoliubov published a book on asymptotic methods in nonlinear oscillations (Bogoliubov & Mitropolsky, 1961) . This book contains their fundamental achievements between 1945 and 1955. In a review of the book, Solomon Lefschetz made the following remarks:
The present book is the fourth or fifth major treatise published in recent years by Soviet scientists on the general topic of nonlinear oscillations, which serves to indicate the great value which is attached in the
USSR
to this general topic. The general program of the book is not too far from the program of the 1937 Krylov-Bogoliubov monograph (Introduction to Nonlinear Mechanics). However, although the book is addressed primarily to physicists and engineers, its mathematical treatment is most careful, which was by no means the case with the 1937 monograph. The book is also much more orderly and most readable: an excellent contribution in every respect.
9. Considerations about Introduction to Nonlinear Mechanics
Krylov and Bogoliubov’s first book, published initially in 1934, was translated to English by Solomon Lefschetz in 1942 (Krylov & Bogoliubov, 1950) . As he emphasized, the authors Krylov and Bogoliubov considered weakly nonlinear equations in terms of small parameters: “Similar equations are well known in astronomy and have been the object of systematic investigation by Lindstedt, Gylden, Lyapunov, and above all by Poincaré. In a general sense, one may say that the same methods are applied by Krylov and Bogoliubov. However, the applications which they have in view are quite different, as they are chiefly in engineering, technology, and physics, notably electrical circuit theory”. This means that the improvements and refinements proposed by Krylov and Bogoliubov are very useful tools for applications in engineering and physics. This small book with around one hundred pages is divided in nine chapters with the following subtitles:
Chapter I: Some Non-Linear Oscillatory Systems
Chapter II: Elementary Theory of the First Approximation
Chapter III: Refinement of the First Approximation
Chapter IV: Construction of the Higher Approximation
Chapter V: Linearization
Chapter VI: Application of Symbolic Methods to Linearization
Chapter VII: Multiply Periodic Systems
Chapter VIII: Influence of Periodic Disturbances
Chapter IX: Complements
Bibliography
In Chapter I, dedicated to selected systems, the following technical problems are studied: the oscillatory shaft, the electrical circuit without resistance, the pendulum freely oscillating in the atmosphere, the electrical circuit with resistance, the electronic generator. Also studied in this chapter are modelling aspects of these problems. Hence, some important equations are presented, such as Raleigh and Van der Pol which became classic in nonlinear investigations. In this context, the coefficients representing friction and energy dissipation appear as fundamental characteristics of some nonlinear systems.
Chapter II, about the solution of the systems presented in Chapter I, is concerned with mathematical modelling and involves equations of the following type:
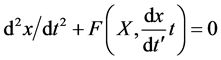 (1)
(1)
The authors then proposed to investigate more particularly the quasi-harmonic case, where there are oscillations near to the sinusoidal response in the form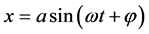 . For this case, and also considering the function F free from the explicit time
. For this case, and also considering the function F free from the explicit time , the basic differential equation is:
, the basic differential equation is:
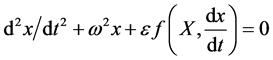 (2)
(2)
where 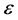 is a small parameter.
is a small parameter.
The difficulty which arose in the eighteenth century, the presence of secular terms, appears again. The objective now is to try a new approximated approach in order to obtain solutions free from these terms.
For 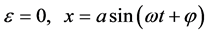 and
and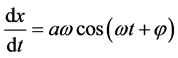 , where
, where 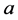 and
and 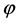
are constant. The method consists of now assuming 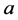 and
and 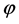 as new unknown functions of the time, which are to be determined so that the solution is sinusoidal.
as new unknown functions of the time, which are to be determined so that the solution is sinusoidal.
The transformations obtained in the original differential equation are such that instead of a single differential equation of the second order, in the unknown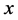 , we have two differential equations of the first order in the unknown
, we have two differential equations of the first order in the unknown 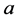 and
and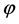 .
.
The system admits that the period 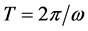 and
and ![]() are proportional
are proportional
to the small parameter, so that ![]() and
and ![]() will be slowly varying functions of time during the period
will be slowly varying functions of time during the period![]() , and as a first approximation we may consider them as constant. Another important remark is that the first approximation solution is obtained from exact solutions by averaging the system with respect to time
, and as a first approximation we may consider them as constant. Another important remark is that the first approximation solution is obtained from exact solutions by averaging the system with respect to time![]() . Thus, the process will be described as the averaging principle. Finally, in this chapter the method is applied to a certain number of known systems.
. Thus, the process will be described as the averaging principle. Finally, in this chapter the method is applied to a certain number of known systems.
In Chapter III, the authors search for a refinement of the previous solution by improving the accuracy of the first approximation, of course, a more complicated one. The new refined first approximation is:
![]() (3)
(3)
where ![]() and
and ![]() are the imposed amplitude and phase angle.
are the imposed amplitude and phase angle.
In other words, ![]() and
and ![]() are the first approximated solution plus terms of order
are the first approximated solution plus terms of order![]() . The method is then applied to the same systems studied in Chapter I.
. The method is then applied to the same systems studied in Chapter I.
Chapter IV, a study of the higher approximations, consists of taking into account the higher harmonics of the same basic equation. This means considering methods for forming approximate solutions corresponding to stationary oscillations which satisfies the basic model, but the solution contains terms in any given power of![]() .
.
As a general conclusion to this chapter, except for certain singular cases, the relations obtained for the first approximation provide the same qualitative results for the starting of self-oscillations as the higher approximations. However, the higher approximations provide quantitative rather than new qualitative information. Thus, because of the difficulty in computing the higher approximation, it is usually sufficient to obtain the first approximation.
Shown in Chapter V, concerned with a method of linearization of the nonlinear system, is that the mathematical model representing the nonlinear system in the first approximation is equivalent to that of a linear system with a dissipation coefficient and a spring constant. The approximation is to the order of![]() , where quantities of the same order are neglected when the first approximation is formed. As a result, the linear system is equivalent to the nonlinear one. Besides this equivalent linearization, another interpretation can also be used.
, where quantities of the same order are neglected when the first approximation is formed. As a result, the linear system is equivalent to the nonlinear one. Besides this equivalent linearization, another interpretation can also be used.
As they are dealing with systems which do not differ much from harmonic systems, a harmonic oscillation in the form ![]() can be used in these relations to obtain the linear force and the harmonic frequency
can be used in these relations to obtain the linear force and the harmonic frequency ![]() The algebraic process is explained in detail in the text and is referred to as the principle of harmonic balance. There is no difficulty in showing that it is in fact equivalent to the first procedure explained above. At the end of the chapter some examples are shown, mainly electrical circuits.
The algebraic process is explained in detail in the text and is referred to as the principle of harmonic balance. There is no difficulty in showing that it is in fact equivalent to the first procedure explained above. At the end of the chapter some examples are shown, mainly electrical circuits.
In Chapter VI, the authors are basically concerned with the application of symbolic methods to linearization where complex algebra is extensively used. If ![]()
is harmonic with period ![]() then
then![]() , where
, where![]() .The
.The
operator ![]() or
or ![]()
Mathematical manipulation using complex algebra is more suitable for the systems studied in the book. For example, we can consider two terminals and impose a harmonic voltage ![]() at the terminals. The corresponding complex voltage is
at the terminals. The corresponding complex voltage is ![]() and thus the complex current is defined by
and thus the complex current is defined by![]() .
.
The operator method can be generalized to be applied to non-stationary oscillations. In a linear system a non-stationary oscillation is of the exponential harmonic type:
![]() (4)
(4)
Hence, if we have a nonlinear system, in the first approximation the solution assumes the form above with ![]() and
and![]() .
.
In Chapter VII, multiplying periodic systems are looked at, and it is asked if it is possible to consider systems with several frequencies instead of the systems considered until now, where we speak about one frequency at a time. For nonlinear systems with multiple frequencies the principle of superposition is not applied to a linear system equivalent to a given nonlinear one. Under certain conditions, such as the reasonable smallness of suitable parameters, some progress was made. For the sake of simplicity the authors limited the discussion to the case of two oscillations. Thus, two distinct situations arise, depending on the presence or absence of resonance.
Both cases were studied. In the non-resonance case, considering the first approximation, the nonlinear characteristic may be replaced by the linear characteristic. We can interpret the replacement of the nonlinear element by an equivalent element with a characteristic just written as a linearization of the system. For the resonant case, the two harmonics ![]() and
and ![]() contain other frequencies which may be smaller than
contain other frequencies which may be smaller than![]() . What we have here is the demultiplication of frequency, a property of considerable practical importance.
. What we have here is the demultiplication of frequency, a property of considerable practical importance.
In Chapter VIII, the system is now subjected to exterior disturbances. As an example of a non-isolated system the following equation is introduced:
![]() (5)
(5)
where![]() ,
, ![]() are positive and
are positive and ![]() is a small parameter.
is a small parameter.
For ![]() small the system is quasi-harmonic and the concept of linearization can be applied. For
small the system is quasi-harmonic and the concept of linearization can be applied. For![]() , we can choose
, we can choose![]() , where
, where![]() .
.
For ![]() small but
small but![]() , we will consider the above formulas as approximations. Two cases are studied, the non-resonant and the resonant. The authors then applied the developments presented to the Van der Pol oscillator.
, we will consider the above formulas as approximations. Two cases are studied, the non-resonant and the resonant. The authors then applied the developments presented to the Van der Pol oscillator.
In Chapter IX, entitled complements, the authors discuss initially other procedures to obtain the higher approximations starting from the approach indicated in Chapter IV. As an example we can select just one of them. It uses the following equation:
![]() (6)
(6)
for ![]() sufficiently small we have a power series representation:
sufficiently small we have a power series representation:
![]() (7)
(7)
in which ![]() is a polynomial in,
is a polynomial in, ![]() ,
, ![]() ,
,![]() .
.
Introducing new variables ![]() and
and ![]() such that
such that![]() .
.
Following this method we can obtain the successive approximations in a direct way, as well as the estimation of the error that appears when certain terms are neglected. Other different procedures are also presented in this chapter in order to obtain approximations solutions of superior order.
We will comment on the bibliography presented by Krylov and Bogoliubov in their first book in our conclusions because it describes important characteristics of their common lines of research before the book was published.
10. Conclusion
The method developed by Bogoliubov and Mitropolskyis much better presented in the book Asymptotic Methods in the Theory of Nonlinear Oscillations. An English translation of the second Russian edition of the book appeared in 1961. It is this work that has come to be known as the KBM method (Krylov-Bogoliubov-Mitropolsky). This book was the first of many books written by Mitropolsky, the majority coauthored with his former doctoral students. Several authors list 31 monographs published by Mitropolsky between 1955 and 2005.
In the preface of the 1971 edition of the above mentioned book Mitropolskystated:
We deal with the method of averaging in nonlinear mechanics. We include numerous results of further development and generalization of the basic ideas of N. N. Bogoliubov. We give various algorithms, schemes and rules for constructing approximate solutions of equations with small and large parameters, and obtain examples which in many cases graphically illustrate the effectiveness of the method of averaging and the breadth of the application to various problems which are, at first glance, very disparate. The theorems that we include reveal the depth and mathematical rigor of the method of averaging. We discuss the basic trends and developments of the method of averaging, and as illustration we give typical examples of nonlinear oscillatory systems, revealing the effectiveness of the method.