Standby Redundancy Allocation for a Coherent System under Its Signature Point Process Representation

Vanderlei da Costa Bueno

Department of Statistics, S?o Paulo University, S?o Paulo, Brazil.

DOI: 10.4236/ajor.2016.66045                

Abstract

Willing to work in reliability theory in a general set up, under stochastically dependence conditions, we intend to characterize a not identically spare standby redundancy operation through compensator transform under a complete information level, the physic approach, that is, observing its component lifetime. We intend to optimize system reliability under standby redundancy allocation of its components, particularly, under minimal standby redundancy. To get results, we will use a coherent system representation through a signature point process.

Keywords

Reliability, Martingale Methods in Reliability Theory, Signature Point Process, Standby Redundancy, Coherent System

1. Introduction

In reliability theory the main application of redundancy is to allocate a redundant spare in a system component position in order to optimize system reliability. For instance, see [1] - [8] , among others.

There are two common types of redundancy used in reliability theory, namely active redundancy, which stochastically leads to consider maximum of random variables and standby redundancy, which stochastically leads to consider convolution of random variables.

For a k-out-of-n system, [1] considers likelihood ratio ordering and gives sufficient conditions to ensure that in a series system the allocation of a standby spare should go to the weakest component while in a parallel system it should go to the strongest. Reference [2] considers the same problem with another criterion of optimality and get the same results. In both above papers, the component lifetimes are stochastically independent and the observations are at system level.

Few papers attained to the case where the components are stochastically dependent. Reference [7] analyzes redundancies for a k-out-of-n system of dependent components. Reference [6] studies active redundancy allocation for a k-out-of-n system of dependent components without simultaneous failures. Reference [5] works a particular form of standby redundancy, called minimal standby redundancy, which gives the component an additional lifetime as it had just before the failure. For the case of dependent components, [5] observes the system at component level and uses the reverse rule of order 2 (RR2) property between compensator processes to investigate the problem of where to allocate a spare in a k-out-of-n system.

In this paper, we intend to analyze a not identically spare standby redundancy allocation for a coherent system of dependent components without simultaneous failures, at component level, under a coherent system signature point process representation and prove that it is optimal to perform standby redundancy on the weakest component of a coherent system in order to optimize system reliability.

In Section 2 we characterize a not identically spare standby redundancy through compensator transform for dependent components. In Section 3 we resume mathematical details of signature point process representation of a coherent system and in Section 4 we investigate the best standby redundancy allocation in a dependent components coherent system in order to optimize system reliability.

2. Not Identically Spare Standby Operation through Compensator Transform

We observe that each component in standby redundancy has two phases, standby and operation under which they can fail. Depending on component failures characteristics during these phases, standby redundancy is classified into the following three types:

1) Hot standby: Each component has the same failure rate regardless of whether it is in standby or in operation. Since the failure rate of one component is unique and is not affected by the other components, the hot standby redundancy consists of stochastically independent components.

2) Warm standby: A standby component can fail, but it has smaller failure rate than the principal component.

Failure characteristics of the component are affected by the other, and warm standby induces dependent component failures.

3) Cold standby: Components does not fail when they are in standby. The components have non-zero failure rates only when they are in operation. A failure of one principal component forces a standby component to start operation and to have a non-zero failure rate. Thus, failure characteristics of one component are affected by the others, and the cold standby redundancy results in mutually dependent component failures.

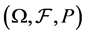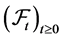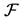In what follows, we consider to observe two lifetimes T and S, which are finite positive random variables defined in a complete probability space through the family of sub -algebras of where

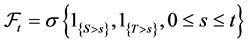
satisfies Dellacherie’s conditions of right continuity and completeness. We assume that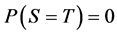, that is, the lifetimes can be dependent but simultaneous failures are ruled out.

In our general set up and in order to simplify the notation, in this paper we assume that relations such as ⫁=, ≤, <, ≠, between random variables and measurable sets, always hold with probability one, which means that the term P-a.s., is suppressed.

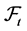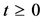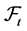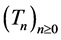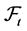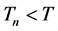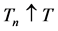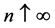We recall that a positive random variable T is a -stopping time if, for every,. The -stopping time T is called predictable if an increasing sequence, of -stopping time, exists such that, as and a 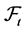-stopping time T is totally inaccessible if 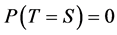for all predictable 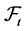-stopping time S. For a mathematical basis of stochastic processes applied to reliability theory see the books of [9] and [10] .

Generally, standby redundancy gives to the component an additional lifetime. In our context the standby operation of S by T is defined as the improvement of S by 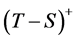and denoted by, where in the set, and is equal to 0 in the set. We remark that, the lifetime interpretations is different of a parallel system lifetime, , which has a null failure rate up to time. The lifetime has the failure rate of S before its failure.

Furthermore, in relation to, and using the Doob-Meyer decomposition, we consider the predictable compensator processes, such that is a zero mean uniformly integral martingale. Also, in relation to , we consider the predictable compensator processes, such that is a zero mean uniformly integral martingale.

The compensator process is expressed in terms of conditional probability, given the available information and generalizes the classical notion of hazard. Intuitively this corresponds to produce whether the failure goes to occur now, on the basis of all observations available up to, but not including, the present.

The well known equivalence between distributions functions and compensator processes follows from [11] and we have,. Therefore and.

In the case of independent lifetimes, the survival function of the improved lifetime by is

Therefore the -compensator of is

In this fashion and preserving the independence case interpretation, we define, for dependent lifetimes, the -compensator of as the sum of the compensator transformations of, and, , with

and

We observe that and implying and getting an improvement of the lifetimes.

Following this thinking, as a predictable compensator is unique we are going to find a probability measure under which is the a -compensator of.

To proceed we consider the compensator transform

.

To prove the main Theorem of this section we are going to use the following Lemma:

Lemma 2.1 Under this section assumptions, the following process

is a nonnegative -martingale with.

Proof We consider the -stopping time defined by

It is sufficient to prove that the process

is a bounded -martingale.

Note that, for any -stopping time we can write

where. The procedure is easy:

On the set we have

Otherwise, on the set

As the integrand

is a -predictable process and is a -martingale, is a -martingale with and we get the result.

Secondly, we consider the compensator transform

and with the same argument used to prove Lemma 2.1 we can prove Lemma 2.2:

Lemma 2.2 Under this section assumptions, the following process

is a nonnegative -martingale with.

Now, we can write the main theorem:

Theorem 2.3 Under this section assumptions, the following process

is a nonnegative local -martingale with.

Proof. Using Lemma 2.1, Lemma 2.2 and the Stieltjes differentiation rule we have

As by assumption and are continuous with, we have

. Therefore is a nonnegative local -martingale with and the theorem is proved.

We are looking for a probability measure Q, such that, under Q, becomes the a -compensator of with respect to this modified probability measure.

Under certain conditions, it is possible to find Q. Indeed assume that the process is uniformly integrable. Then it follows from Girsanov Theorem, see [10] , a well know result on point process martingales, that the desired measure Q is given by the Radon

Nikodyn derivative. The random variable is given by

where.

Remark 2.4. In reference to the first paragraph of this section, in the above setting we can identify the measure with warm standby in which case the component in standby can fail before the component in operation.

In the case of cold standby redundancy, T does not fail before S, we can consider S < T and we have

In the case where T and S are identically distributed, we have and the compensator transform is given by

which can be used to define a standby redundancy through compensator transform when the standby component and the component in operation are stochastically dependent but identically distributed as in [6] .

3. Results in Signature Point Process

Due its importance we present these results in this section which appear in [12] . In our general setup, we consider the vector of n components lifetimes which are finite and positive random variables defined in a complete probability space with for all in, the index set of components. Therefore, the lifetimes can be dependent but simultaneous failures are ruled out.

The evolution of components in time define a marked point process given through the failure times and the corresponding marks. We denote the ordered lifetimes as they appear in time and by the corresponding marks. As a convention we set and

where e is a fictitious mark not in C the index set of the components. The sequence defines a marked point process.

The mathematical description of our observations, the complete information level, is given by a family of sub σ algebras of, denoted by, where

,

satisfies the Dellacherie conditions of right continuity and completeness.

Intuitively, at each time t the observer knows if the event have either occurred or not and if it had, he knows exactly the value and the mark.

We consider, conveniently, the lifetimes defined by the failure event

with their sub-distribution function, suitable standardized

The behavior of the point process, as the information flows continuously in time is given by the following theorem:

Theorem 3.1 Let be the component lifetimes of a coherent system with lifetime T. Then,

Proof. From the total probability rule we have

As T and are -stopping time and it is well known that the event where

,

we conclude that is - measurable. Therefore

.

The above decomposition allows us to define the signature process at component level.

Definition 3.2 The vector is defined as the marked point signature process of the system 𝛷.

Remark 3.3 We note that the above representation can be set in two way. We would prefer the one which preserves the component index because, by example, we could talk about the reliability importance of component j for the system reliability at the k-th failure.

Also, as for all, the collection

form a partition of Ω and Therefore

Remark 3.4 Using Remark 3.3 we can calculate the system reliability as

If the component lifetimes are continuous, independent and identically distributed we have,

recovering the classical result as in [13] .

Remark 3.5 The marked is a -sub-martingale, that is, is -measurable, integrable, and for all.

Follows that, from Doob-Meyer decomposition, there exists an unique predictable process, , , called the -compensator of, such that is a zero mean uniformly integrable -martingale. We assume that are absolutely continuous -compensators processes and that are totally inaccessible -stopping times.

The -compensator of where T is the system lifetime is set in the following theorem:

Theorem 3.6 Let, be the component lifetimes of a coherent system with lifetime T. Then, under the above hypothesis and notation, the -sub-martingale, has the -compensator

Proof. We consider the process

It is left continuous and -predictable. Therefore

is a -martingale. As a finite sum of -martingales is a -martingale

is a -martingale. As the compensator is unique we get the result.

4. Standby Redundancy in a Coherent System of Dependent Components

We are concerned with the problem of where to allocate a spare component using standby redundancy in a coherent system in order to optimize system reliability improvement. We let be the lifetime of a coherent system with component lifetimes, , for all under the hypothesis and notation of Section 3. Furthermore, let be the systems lifetime resulting from an standby redundancy operation of component i through a spare with lifetime S, not identically distributed as. In particular we count this system failure through a counting process with -compensator. To compare the systems lifetime resulting from redundancy operations we are going to compare the component point processes compensators through cumulative hazard order as in [14]

Definition 4.1 Consider two point processes, corresponding to the component lifetimes vector T defined in a complete probability space and, in relation to the component lifetimes vector S possibly defined on a different probability space, with corresponding continuous compensator processes

which are, almost surely, continuous in t. If for all and for all and , we say that S is smaller than T in the cumulative hazard order, denoted by.

Also, we are going to use the following result from [15] .

Theorem 4.2 Consider two point processes, corresponding to the component lifetimes vector T defined in a complete probability space and, corresponding to the component lifetimes vector S possibly defined on a different probability space. If S is smaller than T in cumulative hazard order, , then

for all decreasing real and right continuous function with left hand limits 𝜓, which implies.

4.1. Minimal Standby Redundancy in a Coherent System of Dependent Components

In this first subsection we resume the results from [5] intending to present a generalization of the main theorem from a k-out-of-n system to coherent systems. Intuitively, a minimal standby redundancy gives to the component an additional lifetime as it had just before the failure.

In a random environment where the component is affected by the behavior of other components, [5] find a compensator approach for minimal standby redundancy considering the Girsanov’s theorem argument where the component compensators process of is transformed through

with and for.

The result is: under the measure Q defined by the Radon Nikodin derivative, is the component compensator transform of.

Observe that

and, in the absolutely continuous case, where, [11] , we can recover, in the independence case, the classical expression

Recovering our setting, let, the system lifetime resulting from an minimal standby redundancy operation of the lifetime, of component i. We count this system failure through a counting process with -compensator.

Theorem 4.1.1 Let be let be the lifetime of a coherent system with component lifetimes, , for all. Under a minimal standby redundancy operation, the hypothesis and notation of Section 3, if, then.

Proof From Theorem 3.6 we have to compare system’s compensators expectation values on the form

for where the notation means the restriction of, to the interval. Clearly, it is sufficient to prove for and.

The final result follows from Theorem 4.2

4.2. Standby Redundancy in a Coherent System of Dependent Components

In what follows we consider an unique spare with lifetime S, as in Section 2, with compensator processes, such that is a zero mean uniformly integral martingale, to be allocated between the components, in order to optimize system reliability:

Theorem 4.2.1 Let be let be the lifetime of a coherent system with component lifetimes, , for all. Under standby redundancy and the hypothesis and notation of Section 3, if , then.

Proof. Follows, from Section 2, that the standby redundancy through compensator transform of the component i by a spare with compensator is

Clearly, it is sufficient to prove for and.

The final result follows from Theorem 4.2.

As by hypothesis, we are considering component i weaker than component j in the sense that the hazard process for failure of component i is larger than the hazard process for failure of component j, its also implies that is stochastically less than. Therefore, under Theorem 4.2.1 we understand that, at component level, it is optimal to perform active redundancy allocation on the weakest component of a coherent system of continuous dependent components with no simultaneous failures.

We can, also consider two spares with lifetimes and, with -compensator and with -compensator, to be allocated between the components, in order to optimize system reliability. The following corollary can be easily proved using the same argument of Theorem 4.2.1.

Corollary 4.2. Let be let be the lifetime of a coherent system with component lifetimes, , for all. Under standby redundancy and the hypothesis and notation of Section 3, if and, then, where

5. Conclusions

An efficient method to optimize the reliability of a coherent system is to add redundancy components to the system. Therefore it is very significant to know about the allocation which best optimizes system reliability.

In the last decade, many researchers devoted themselves to this topic, in general analyzing k-out-of-n systems and following a natural and classical approach: considering that the components lifetimes were stochastically independent and to observing the system at its level through

Few papers attempt to the case where the components are stochastically dependent without simultaneous failures. [5] and [6] consider stochastically dependent components lifetime and observe the complete information at components’ level

getting results for k-out-of-n systems.

With recent results in signature theory and its extension to a signature point process, we generalize results from k-out-of-n to coherent systems, particularly for minimal standby redundancy and standby redundancy.

It is also important to note the characterization of standby operation results with not identically spare. The discussion about this new approach and the classical one can be set comparing results of with. We conclude that, at component level, it is optimal to perform active redundancy allocation on the weakest component of a coherent system of continuous dependent components with no simultaneous failures when using the hazard rate ordering between the components lifetimes.

Acknowledgements

This work was partially supported by São Paulo Research Foundation (FAPESP), grant 2015/02249-1.

Conflicts of Interest

The authors declare no conflicts of interest.

References

[1]	Boland, P.J., El Neweihi, E. and Proschan, F. (1992) Stochastic Order for Redundancy Allocation in Series and Parallel Systems. Advanced Applied Probability, 4, 161-171. https://doi.org/10.1017/S0001867800024216
[2]	Singh, H. and Misra, N. (1994) On Redundancy Allocation in Systems. Journal of Applied Probability, 31, 1004-1014. https://doi.org/10.1017/S0021900200099526
[3]	Kuo, W., Prasad, V.R. Tilman, F. and Hwang, L. (2001) Optimal Reliability Design. Cambridge University Press, Cambridge
[4]	Prasad, V.R., Kuo, W. and Kim, K.M. (1999) Optimal Allocation of Identical, Multi Functional Spears in a Series System. IEEE Transactions on Reliability, 48, 118-126. https://doi.org/10.1109/24.784269
[5]	Bueno, V.C. (2005) Minimal Standby Redundancy Allocation in a k-out-of-n:F System of Dependent Components. European Journal of Operational Research, 165, 786-793. https://doi.org/10.1016/j.ejor.2003.01.004
[6]	Bueno, V.C. and Carmo, I.M. (2007) Active Redundancy Allocation for a k-out-of-n:F System of Dependent Components. European Journal of Operational Research, 176, 1041-1051. https://doi.org/10.1016/j.ejor.2005.09.012
[7]	Belzunce, F. Martinez-Puertas, H. and Ruiz, J.M. (2013) On Allocation of Redundant Components for Systems with Dependent Components. European Journal of Operational Research, 230, 573-580. https://doi.org/10.1016/j.ejor.2013.05.004
[8]	Zhao, P., Chan, P.S. and Li, L. (2015) Redundancy Allocation at Component Level versus System Level. European Journal of Operational Research, 241, 402-411. https://doi.org/10.1016/j.ejor.2014.08.040
[9]	Aven, T. and Jensen, U. (1999) Stochastic Models in Reliability. Springer Verlag, New York. https://doi.org/10.1007/b97596
[10]	Bremaud, P. (1981) Point Processes and Queues: Martingales Dynamics. Springer Verlag, New York. https://doi.org/10.1007/978-1-4684-9477-8
[11]	Arjas, E. and Yashin, A. (1988) A Note on Random Intensities and Conditional Survival Functions. Journal of Applied Probability, 25, 630-635. https://doi.org/10.1017/S0021900200041346
[12]	Bueno, V.C. (2016) Signature Point Processes. Lambert Academic Publishing, Saarbrucken, Germany.
[13]	Samaniego, F.J. (1985) On Closure of the IFR Class under Formation of Coherent Systems. IEEE Transactions on Reliability, 34, 69-72. https://doi.org/10.1109/TR.1985.5221935
[14]	Shaked, M. and Shanthikumar, J.G. (1994) Stochastic Orders and their Applications. Academic Press, New York.
[15]	Kwiecinski, A. and Szekli, R. (1991) Compensator Conditions for Stochastic Ordering of Point Processes. Journal of Applied Probability, 28, 751-756. https://doi.org/10.1017/S0021900200042662