High Dimensionality Effects on the Efficient Frontier: A Tri-Nation Study ()
Received 5 December 2015; accepted 12 February 2016; published 15 February 2016

1. Introduction
The need for solutions to optimization problems in a high dimensional setting is increasing in the finance industry with huge amount of data being generated every day. Many empirical studies indicate that minimum variance portfolios in general lead to a better out-of-sample performance than stock index portfolios [2] [3] . Markowitz Portfolio theory, the most popular method for portfolio optimization, develops a serious drawback namely risk underestimation. When implementing portfolio optimization according to [4] , one needs to estimate the expected asset returns as well as the corresponding variances and covariances. El Karoui studied the Markowitz problem as a solution to quadratic problems in [1] and [5] to establish a relationship between the two types of solution viz. one computed using population data and another estimated from sample data. This relationship is important and particularly relevant for high dimensional data where one suspects that the difference between the two may be considerable.
There is a broad literature which addresses the question of how to reduce estimation risk in portfolio optimization. De Miguel et al. compare portfolio strategies which differ in the treatment of estimation risk in [6] and confirm that the considered strategies perform better than the traditional plug-in implementation of Markowitz optimization. Constrained minimum-variance portfolios have been frequently advocated in the literature (see [7] - [10] ).
The main aim of this paper is to compare the efficient frontier for real data based on corrected estimators of [5] and norm-constrained portfolios. One natural advantage of norm-constrained optimization is that it leads to sparse solutions, which many of the portfolio weights are zero. Such a portfolio is preferable in terms of transaction costs. On the other hand, if Gaussian assumptions are valid, then the corrected frontier is indeed the most efficient. Another advantage is that one can obtain a confidence interval for the variance at each value of return.
We carry out our analysis for three scenarios namely the Indian stock market, London Stock market and U.S stock market to facilitate a comparative study and to conclude about the uniformity of our results. We use constituent stocks of NSE CNX 100, FTSE 100 and S&P 100 respectively for the three scenarios as our data base taking daily data from 1st Jan 2013 to 1st Jan 2014 time span. The daily returns data are publicly available from NSE India and yahoo finance. Thus we have at our disposal, 100 stocks for each country with 250 observations per stock. In other words, considering p to be the number of assets and n to be the number of observations per asset, we arrive at a large p, large n setting which in modern statistical parlance can be considered to be a high dimensional setting.
The rest of the paper is organized as follows. Section 2 is committed to explaining the modern portfolio theory. Section 3 deals with identifying the underestimation factors and the bias inherent in the plug in estimators and subsequently eliminating them from the empirical optimized portfolio, to arrive at the final error-free optimized weights. Section 4 deals with norm constrained models. In section 5, we present the empirical results of comparing the efficient frontiers obtained from Markowitz portfolio to error-free efficient frontier and norm constrained portfolio efficient frontiers. We present our conclusions in section 6.
2. Markowitz Portfolio Theory
Markowitz portfolio theory [4] is a classic portfolio optimization problem in finance where investors choose to invest according to the following framework: one picks the assets in such a way that the portfolio guarantees a certain level of expected returns but minimizes the “risk” associated with it. In standard framework this risk is measured by the variance of the portfolio whereas the expectation by the mean of the portfolio. The set-up is as follows:
There is an opportunity to invest in p assets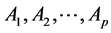 .
.
The mean returns are represented by a p-dimensional vector .
.
The covariance matrix of the returns is denoted by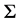 .
.
The aim is to create a portfolio with guaranteed mean return 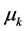 and minimize the risk as measured by the variance.
and minimize the risk as measured by the variance.
The problem is to find the weights or amount allocated to various assets of the portfolio.
Note that 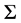 is positive semi definite and symmetric. In ideal situation the means, variances and covariance are known and the problem is the following quadratic programming problem:
is positive semi definite and symmetric. In ideal situation the means, variances and covariance are known and the problem is the following quadratic programming problem:
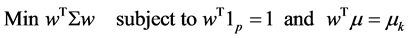 (1)
(1)
Here 1p is a p-dimensional vector with one in every entry.
In practice, Σ and µ are unknown. The most common procedure known as plug-in implementation replaces them with their sample estimators as follows to obtain the optimal weights.
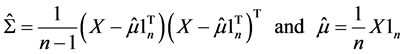 (2)
(2)
With 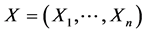 is a p × n matrix of the returns of the assets. It is assumed that the columns of X are independent multivariate Normal vectors
is a p × n matrix of the returns of the assets. It is assumed that the columns of X are independent multivariate Normal vectors
If 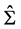 is invertible with
is invertible with 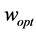 is representing the solution of the above quadratic problem then,
is representing the solution of the above quadratic problem then,
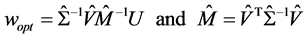 (3)
(3)
where 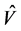 a p × 2 matrix is whose first column are all unity and second column are the estimated means. Also U is the 2 dimensional vector with first entry being 1 and the second entry being
a p × 2 matrix is whose first column are all unity and second column are the estimated means. Also U is the 2 dimensional vector with first entry being 1 and the second entry being .
.
The curve 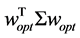 seen as a function of
seen as a function of 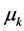 is called the efficient frontier.
is called the efficient frontier.
3. Corrected Frontier Using Gaussian Assumption
In the Markowitz setting, let us assume that the returns have normal distribution. We shall assume n and p both go to infinity and each Xi ~ Np (µ, S) independently and identically. The parameters of the distribution are estimated using sample estimators defined in (2).
We have from Corollary 3.3 of [1] ,
![]() (4)
(4)
where ![]() is the population quantity, k being the number of constraints in the quadratic problem we are solving which in our case will be equal to 2,
is the population quantity, k being the number of constraints in the quadratic problem we are solving which in our case will be equal to 2, ![]() represents the weights obtained from the empirical data
represents the weights obtained from the empirical data
at hand while ![]() is its population counterpart.
is its population counterpart. ![]() denotes the canonical basis vectors in
denotes the canonical basis vectors in![]() . The corollary shows that the effects of both covariance and mean estimation are to underestimate the risk and the empirical frontier is asymptotically deterministic. The cost of not knowing the covariance matrix and estimating it is captured
. The corollary shows that the effects of both covariance and mean estimation are to underestimate the risk and the empirical frontier is asymptotically deterministic. The cost of not knowing the covariance matrix and estimating it is captured
in the factor![]() . In other words using plug in procedures leads to over optimistic conclusions in this situation.
. In other words using plug in procedures leads to over optimistic conclusions in this situation.
Also when ![]() and
and ![]() and we denote
and we denote ![]() the impact of the estimation of µ by
the impact of the estimation of µ by ![]() will be risk underestimation by the amount
will be risk underestimation by the amount![]() . Hence rearranging (4) and subtracting the bias associated with mean and covariance estimation, from our variances obtained from sample data we get the error-free actual quantities of interest. In other words,
. Hence rearranging (4) and subtracting the bias associated with mean and covariance estimation, from our variances obtained from sample data we get the error-free actual quantities of interest. In other words,
![]() (5)
(5)
The estimator ![]() for proposed in [1] is a modified version of the optimal solution in equation (3). The modification is to replace M by
for proposed in [1] is a modified version of the optimal solution in equation (3). The modification is to replace M by![]() .
.
It is also shown in Theorem 5.1 of [1] that the risk is indeed underestimated by the empirical frontier. Specifically,
![]()
where ![]() and
and ![]() are respectively the empirical frontier with Gaussian distributed data and the theoretical efficient frontier.
are respectively the empirical frontier with Gaussian distributed data and the theoretical efficient frontier.
We use the 95% confidence intervals for the variance of a single Normal variable with unknown mean µ and standard deviation σ given by:
![]()
where ![]() is the sample variance and
is the sample variance and ![]() follows a
follows a ![]() distribution with
distribution with ![]() degrees of freedom, the confidence coefficient being equal to 0.05.
degrees of freedom, the confidence coefficient being equal to 0.05.
4. Constraining the Portfolio
The short sale constrained minimum-variance portfolio, ![]() is introduced in [7] . This is the solution to problem (1) with the additional constraint that the portfolio weights be nonnegative.
is introduced in [7] . This is the solution to problem (1) with the additional constraint that the portfolio weights be nonnegative.
4.1. 1-Norm Constrained Portfolio
The 1-norm-constrained portfolio, ![]() , is the solution to the traditional minimum-variance portfolio problem (1) subject to the additional constraint that the L1-norm of the portfolio-weight vector be smaller than or equal to a certain threshold c; that is,
, is the solution to the traditional minimum-variance portfolio problem (1) subject to the additional constraint that the L1-norm of the portfolio-weight vector be smaller than or equal to a certain threshold c; that is,
![]() (6)
(6)
1-norm constrained portfolio problem can be summarized as
![]() (7)
(7)
Markowitz risk minimization problem can be recast as a regression problem.
![]() (8)
(8)
By using the fact that the sum of total weights is one, we have
![]() (9)
(9)
where R = Return vector, ![]() and
and ![]() where
where![]() .
.
Finding the optimal weight w is the same as finding the regression coefficient![]() . The gross-exposure constraint
. The gross-exposure constraint ![]() can now be expressed as
can now be expressed as![]() . Thus the problem (7) is similar to
. Thus the problem (7) is similar to
![]() (10)
(10)
where ![]() but they are not equivalent. The latter depends on choice of Y, while the former
but they are not equivalent. The latter depends on choice of Y, while the former
does not. Efron et al. developed an efficient algorithm in [11] by using the least-angle regression (LARS), called the LARS-LASSO algorithm, to efficiently find the whole solution path![]() , for all
, for all![]() , to (10). The number of non-vanishing weights varies as c ranges from 0 to ∞. It recruits successively more assets and gradually all assets. The algorithm works iteratively as follows:
, to (10). The number of non-vanishing weights varies as c ranges from 0 to ∞. It recruits successively more assets and gradually all assets. The algorithm works iteratively as follows:
![]() (11)
(11)
Here our objective is to minimize the out-of-sample portfolio variance. To choose c we use leave-one-out- cross validation (see [12] ).
4.2. 2-Norm Constrained Portfolio
The 2-norm-constrained portfolio, ![]() , is the solution to the traditional minimum-variance portfolio problem (1) subject to the additional constraint that the L2-norm of the portfolio-weight vector is smaller than or equal to a certain threshold c; that is,
, is the solution to the traditional minimum-variance portfolio problem (1) subject to the additional constraint that the L2-norm of the portfolio-weight vector is smaller than or equal to a certain threshold c; that is,
![]() (12)
(12)
2-norm constrained portfolio problem can be summarized as
![]() (13)
(13)
Similar to the 1-norm constrained portfolio finding the optimal weight w in this case is the same as finding the regression coefficient![]() .
.
The gross-exposure constraint ![]() can now be expressed as
can now be expressed as![]() . Thus the problem (13) is similar to
. Thus the problem (13) is similar to
![]() (14)
(14)
where![]() . But they are not equivalent. The latter depends on the choice of asset Y, while the former does not.
. But they are not equivalent. The latter depends on the choice of asset Y, while the former does not.
The whole solution pat ![]() to (14), for all c ≥ 0, can be efficiently obtained by the regularization algorithm of Ridge regression (see [13] ). The number of non-vanishing weights varies as c ranges from 0 to ∞. It recruits successively more assets and gradually all assets. The algorithm works iteratively as follows:
to (14), for all c ≥ 0, can be efficiently obtained by the regularization algorithm of Ridge regression (see [13] ). The number of non-vanishing weights varies as c ranges from 0 to ∞. It recruits successively more assets and gradually all assets. The algorithm works iteratively as follows:
![]() (15)
(15)
To choose c we use cross validation, as in the case of 1-norm constrained portfolio.
5. Practical Results
Below we provide an overview of our results of Markowitz efficient frontier, corrected frontier using Gaussian assumption, 1-norm and 2-norm constrained efficient frontiers for the 3 countries.
In Figures 1-3, we present the efficient frontiers using the different methods. The dashed lines represent the empirical 95% confidence intervals computed for a fixed expected return. The x-axis is variance and y-axis is
![]()
Figure 1. Efficient frontier of US data.
![]()
Figure 2. Efficient frontier of UK data.
![]()
Figure 3. Efficient frontier of Indian data.
expected returns. We have considered the same set of µ’s and Σ’s, for each individual country to keep the results comparable. It can be concluded from the relative positions of the corrected and uncorrected efficient frontiers that the risk is indeed underestimated in case of high dimensional data. But comparing to 2-norm and 1-norm constrained portfolios as they outperform the corrected frontiers. The constrained portfolios are, in general, less efficient than the corrected portfolio, in the sense that they have higher variance for each fixed level of return. Of course constrained portfolios have their own advantages due to sparsity that might out-weigh the loss in efficiency. For the 1-norm and 2-norm portfolios, the choice of the asset Y is important. We have chosen Y to be the no short sale portfolio in all our computations. For each country, the 2-norm portfolio is most efficient among the constrained portfolios and the 1-norm is not monotone.
The amount of shrinkage or regularization is directly related to the number of stocks included in the optimal portfolio. In Figure 4 we present this for the 1-norm constrained portfolio. As expected, this is an increasing function of c, the bound on the L1 norm. For almost all values of c, the number of stocks in the portfolio is highest for the Indian market and lowest for the US market. Results for the L2norm are similar.
For out of sample performance we first created portfolios for all the three datasets using the return data for the first 230 trading days. These portfolios are then held for one month and rebalanced at the end next month. The summary statistics of these portfolios are presented for the three datasets as box-plots in Figures 5-7. 1-norm constrained portfolios were created for c = 2 and c = 3 for all the three nations. 2-norm constrained portfolios were created for the optimal c chosen by cross validation, as mentioned in Section 4. This value equals 1.2544, 1.14 and 1.0739 respectively for US, UK and Indian data.
The out-of-sample performance is very different for the three markets. For the US data, the 2-normcon-
![]()
Figure 4. Number of stocks with respect to c with Y = “No short sale”.
![]()
Figure 5. Out of sample performance of different portfolios for US data.
![]()
Figure 6. Out of sample performance of different portfolios for UK data.
![]()
Figure 7. Out of sample performance of different portfolios for Indian data.
strained, corrected and no-short-sale portfolios have close to zero average returns while the other methods yield negative average returns. The variances are almost same for all methods except the Markowitz, which has a lower variance. For UK data, the 1-norm with c = 3 and corrected portfolios have significantly negative average return while others have small positive or zero average returns. The variances are almost all the same. For the Indian data, all portfolios except the Markowitz have high positive average returns. In particular, the corrected portfolio has very high average returns, but the variance is also quite high. Overall, from the out-of-sample results, the 2-norm constrained portfolio has higher average and comparable variance to the Markowitz portfolio in all the markets.
6. Conclusion
In this paper we study the effect of high dimension on the efficient frontier with real data on three markets. In particular we study how the recently suggested methods of corrected frontier based on normality assumptions and norm-constrained methods perform relative to Markowitz portfolio optimization. We observe that the Markowitz solution indeed leads to biased estimates of risk that can be improved with the corrected estimates. The norm-constrained methods are comparable and need less model assumptions. Alternative methods of improving the covariance matrix estimation are Bayesian shrinkage approach [8] or random matrix theory and principal component analysis [14] . We have ignored the time component of the data and treated the observations as i.i.d. A further improvement will be to take into account this aspect and model the high dimensional time series as in [15] .