Filtering Function Method for the Cauchy Problem of a Semi-Linear Elliptic Equation ()
Received 3 November 2015; accepted 14 December 2015; published 17 December 2015


1. Introduction
Let 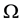 be a bounded, connected domain in
be a bounded, connected domain in 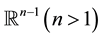 with a smooth boundary
with a smooth boundary 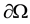 and assume that H is a real Hilbert space. We consider the following Cauchy problem of a semi-linear elliptic partial differential equation
and assume that H is a real Hilbert space. We consider the following Cauchy problem of a semi-linear elliptic partial differential equation
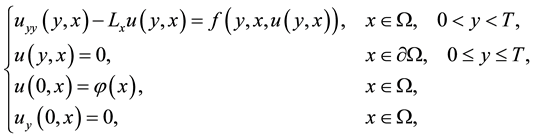 (1.1)
(1.1)
where 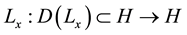 denotes a linear densely defined self-adjoint and positive-definite operator with respect to x. The function
denotes a linear densely defined self-adjoint and positive-definite operator with respect to x. The function  is known, and
is known, and 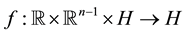 is an uniform Lipschitz continuous function, i.e., existing
is an uniform Lipschitz continuous function, i.e., existing 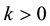 independent of
independent of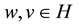 ,
, 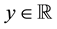 ,
, 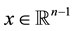 such that
such that
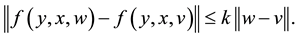 (1.2)
(1.2)
Further, we suppose 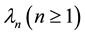 be the eigenvalues of the operator
be the eigenvalues of the operator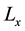 , i.e., for the boundary value problem
, i.e., for the boundary value problem
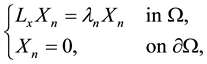 (1.3)
(1.3)
there exists a nontrivial solution![]() . And
. And ![]() satisfy
satisfy
![]() (1.4)
(1.4)
Our problem is to determine ![]() from problem (1.1).
from problem (1.1).
Problem (1.1) is severely ill-posed, i.e., a small perturbation in the given Cauchy data may result in a dramatic error on the solution [1] . Thus regularization techniques are required to stabilize numerical computations, (see [1] [2] ). We know that, as the right term![]() , it is the Cauchy problem of the homogeneous elliptic equations. For the homogeneous problem, there have many regularization methods to deal with it, (see [3] -[8] ). We note that, these references mainly consider the Cauchy problem of linear homogeneous elliptic operator equation, but the literature which involves the semi-linear cases is quite scarce. In 2014, [9] considered the problem (1.1), where the authors used Fourier truncated method to solve it and derived the convergence estimate of logarithmic type. Recently, there are some similar works about the Cauchy problem for nonlinear elliptic equation, and they have been published, such as [10] [11] .
, it is the Cauchy problem of the homogeneous elliptic equations. For the homogeneous problem, there have many regularization methods to deal with it, (see [3] -[8] ). We note that, these references mainly consider the Cauchy problem of linear homogeneous elliptic operator equation, but the literature which involves the semi-linear cases is quite scarce. In 2014, [9] considered the problem (1.1), where the authors used Fourier truncated method to solve it and derived the convergence estimate of logarithmic type. Recently, there are some similar works about the Cauchy problem for nonlinear elliptic equation, and they have been published, such as [10] [11] .
In the present paper, we adopt a filtering function method to deal with this problem. The idea of this method is similar to the ones in [4] [5] [12] [13] , etc. However, note that our method here is new and different from them in the above references (see Section 2). Meanwhile we will derive the convergence estimate of Hölder type for this method, which is an improvement for the result in [9] .
This paper is organized as follows. In Section 2, we use the filtering function method to treat problem (1.1) and prove some well-posed results (the existence, uniqueness and stability for the regularization solution). In Section 3, a Hölder type convergence estimate for the regularized method is derived under an a-priori bound assumption for the exact solution. Numerical results are shown in Section 4. Some conclusions are given in Section 5.
2. Filtering Function Method and Some Well-Posed Results
2.1. Filtering Function Method
We assume there exists a solution to problem (1.1), then it satisfies the following nonlinear integral equation (see [9] )
![]() (2.1)
(2.1)
here, ![]() are the orthonormal eigenfunctions for the operator
are the orthonormal eigenfunctions for the operator![]() , and
, and
![]() (2.2)
(2.2)
![]() is the inner product in H.
is the inner product in H.
From (2.1), we can see that the functions![]() ,
, ![]() tend to infinity (as
tend to infinity (as![]() ),
),
so in order to guarantee the convergence of solution![]() , the high frequencies(
, the high frequencies(![]() ) of two functions need to be eliminated. Therefore, a natural way is to use a filter function
) of two functions need to be eliminated. Therefore, a natural way is to use a filter function ![]() to filter out the high
to filter out the high
frequencies of![]() ,
, ![]() and obtain a stable approximate solution, this is so-
and obtain a stable approximate solution, this is so-
called filtering function method.
Let ![]() be the noisy data, and satisfying
be the noisy data, and satisfying
![]() (2.3)
(2.3)
where ![]() is the error level,
is the error level, ![]() is the H-norm. According to the above description, for
is the H-norm. According to the above description, for![]() , we choose the
, we choose the
filter function![]() , and define the following regularization solution
, and define the following regularization solution
![]() (2.4)
(2.4)
where, ![]() ,
,![]() .
.
In fact, it can be verified that (2.4) satisfies the following mixed boundary value problem formally
![]() (2.5)
(2.5)
Our idea is to approximate the exact solution (2.1) by the regularization solution (2.4), i.e., using the solution of (2.5) to approximate the one of (1.1).
2.2. Some Well-Posed Results
Let![]() ,
, ![]() , for the fixed
, for the fixed![]() , we define the function
, we define the function
![]() (2.6)
(2.6)
then ![]() attain unique maximum at the point
attain unique maximum at the point![]() , and from
, and from![]() ,
, ![]() , we have
, we have
![]() (2.7)
(2.7)
note that, when![]() , it can be obtained that
, it can be obtained that
![]() (2.8)
(2.8)
Now, we prove that the problem (2.4) is well-posed (existence, uniqueness and stability for the regularization solution), the proof mentality of Theorem 2.1 mainly comes from the references [14] , which describes the ex- istence and uniqueness for the solution of (2.4).
Theorem 2.1. Let![]() , f satisfies (1.2), then the problem (2.4) exists a unique solution
, f satisfies (1.2), then the problem (2.4) exists a unique solution ![]() .
.
Proof. For![]() , we consider the operator
, we consider the operator ![]() defined by
defined by
![]() (2.9)
(2.9)
then for![]() ,
, ![]() , we can prove the following estimate is valid
, we can prove the following estimate is valid
![]() (2.10)
(2.10)
where![]() ,
, ![]() denotes the sup norm in
denotes the sup norm in![]() .
.
For![]() , we firstly use the induction principle to prove
, we firstly use the induction principle to prove
![]() (2.11)
(2.11)
Note that, for![]() , from (2.7),
, from (2.7),![]() . Meanwhile, use the basic inequalities
. Meanwhile, use the basic inequalities
![]() ,
, ![]() , and
, and![]() . When
. When![]() , from
, from
(2.9), (1.2), we have
![]()
When![]() , we suppose
, we suppose
![]() (2.12)
(2.12)
then for![]() , by (2.12), it similarly can be proven that
, by (2.12), it similarly can be proven that
![]()
By the induction principle, we can obtain that
![]() (2.13)
(2.13)
hence, it is clear that
![]() (2.14)
(2.14)
We consider![]() , and from real analysis, we know
, and from real analysis, we know
![]() (2.15)
(2.15)
There must exist a positive integer number![]() , such that
, such that![]() , therefore
, therefore ![]() is a contraction,
is a contraction,
it shows that the equation ![]() has a unique solution
has a unique solution![]() . Noting that
. Noting that
![]() , thus,
, thus,![]() . By the uniqueness of the fixed point of
. By the uniqueness of the fixed point of![]() , we have
, we have![]() , so the equation
, so the equation ![]() has a unique solution
has a unique solution![]() . □
. □
In the following, we give and prove the stability of the regularization solution.
Theorem 2.2 Suppose f satisfies (1.2), ![]() and
and ![]() be the solutions of problem (2.4) corresponding to the
be the solutions of problem (2.4) corresponding to the
measured datum ![]() and
and![]() , respectively, then for
, respectively, then for![]() , we have
, we have
![]() (2.16)
(2.16)
where![]() .
.
Proof. From (2.4), we have
![]() (2.17)
(2.17)
![]() (2.18)
(2.18)
where![]() ,
,![]() .
.
By (2.17), (2.18), (2.7), (2.8) and (1.2), we have
![]()
Subsequently,
![]()
using Gronwall’s inequality [15] , we have
![]() (2.19)
(2.19)
then from the above inequality (2.19), the stability result (2.16) can be obtained. □
3. Convergence Estimate
In this section, under an a-priori bound assumption for the exact solution a convergence estimate of Hölder type for the regularization method is derived. The corresponding result is shown in Theorem 3.1.
Theorem 3.1. Suppose that f satisfies the uniform Lipschitz condition (1.2), and u given by (2.1) is the exact solution of problem (1.1), ![]() defined by (2.4) is the regularization solution, the measured data
defined by (2.4) is the regularization solution, the measured data ![]() satisfies (2.3). If the exact solution u satisfies
satisfies (2.3). If the exact solution u satisfies
![]() (3.1)
(3.1)
and the regularization parameter ![]() is chosen as
is chosen as
![]() (3.2)
(3.2)
then for fixed![]() , we have the following convergence estimate
, we have the following convergence estimate
![]() (3.3)
(3.3)
here![]() ,
, ![]() ,
, ![]() is given in Theorem 2.2.
is given in Theorem 2.2.
Proof. Denote ![]() be the solution of problem (2.4) with exact data
be the solution of problem (2.4) with exact data![]() . We know that
. We know that
![]() (3.4)
(3.4)
From Theorem 2.2, for![]() , we have
, we have
![]() (3.5)
(3.5)
By (2.1), (2.4), (2.7), (2.8), we have
![]()
For![]() , we get
, we get
![]() (3.6)
(3.6)
use Gronwall’s inequality [15] , it can be obtained that
![]()
thus
![]() (3.7)
(3.7)
From (3.2), (3.4), (3.5), (3.7) and (2.3), we can obtain the convergence result (3.3). □
4. Numerical Experiments
In this section, we verify the accuracy and efficiency of our given regularization method by the following numerical example
![]() (4.1)
(4.1)
here we take![]() ,
, ![]() ,
, ![]() , then
, then ![]() and
and![]() .
.
It is clear that ![]() is an exact solution of problem (4.1), thus
is an exact solution of problem (4.1), thus
![]() ,
,![]() . We choose the measured
. We choose the measured
data as![]() , where
, where ![]() is an error level, and
is an error level, and
![]() (4.2)
(4.2)
Let ![]() for
for![]() , the regularization solution
, the regularization solution ![]() with
with
![]() can be computed by the following iteration scheme
can be computed by the following iteration scheme
![]() (4.3)
(4.3)
here![]() , and
, and
![]() (4.4)
(4.4)
![]() (4.5)
(4.5)
For a fixed![]() , in order to make the sensitivity analysis for numerical results, we define the relative root mean square error between the exact and approximate solutions as
, in order to make the sensitivity analysis for numerical results, we define the relative root mean square error between the exact and approximate solutions as
![]() (4.6)
(4.6)
We adopt the above given algorithms to compute the regularization solution at ![]() with
with![]() ,
,
for ![]() Taking
Taking ![]() for
for ![]() the numerical results for
the numerical results for ![]() and
and ![]() at
at![]() ,
, ![]() are shown in Figure 1 and Figure 2, respectively. For
are shown in Figure 1 and Figure 2, respectively. For![]() , the relative root mean square errors for the various error levels
, the relative root mean square errors for the various error levels ![]() and regularization parameters
and regularization parameters ![]() at
at ![]() are shown in Table 1. In the computational procedure, the regulari- zation parameter
are shown in Table 1. In the computational procedure, the regulari- zation parameter ![]() is chosen by (3.2), and
is chosen by (3.2), and ![]() is computed by (4.2).
is computed by (4.2).
From Figure 1 and Figure 2 and Table 1, it can be observed that our regularization method is effective and stable. Meanwhile we note that the smaller ![]() is, the better the calculation effect is. Table 1 shows that the numerical results become worse when y approaches to 1, which is a common phenomenon in the computation of ill-posed Cauchy problems for the elliptic equation.
is, the better the calculation effect is. Table 1 shows that the numerical results become worse when y approaches to 1, which is a common phenomenon in the computation of ill-posed Cauchy problems for the elliptic equation.
5. Conclusion
We use a filtering function method to solve a Cauchy problem for semi-linear elliptic equation. The results of the well-posedness for the approximation problem are given. Under the a-priori bound assumption, the conver- gence estimate of Hölder type has been derived. Finally, we compute the regularization solution by constructing an iterative scheme. Some numerical results show that this method is stable and feasible.
Acknowledgements
The authors would like to thank the reviewers for their constructive comments and valuable suggestions that improve the quality of our paper. The work described in this paper was supported by the SRF (2014XYZ08, 2015JBK423), NFPBP (2014QZP02) of Beifang University of Nationalities, the SRP of Ningxia Higher School (NGY20140149) and SRP of State Ethnic Affairs Commission of China (14BFZ004).
NOTES
![]()
*Corresponding author.