Received 5 September 2015; accepted 13 December 2015; published 16 December 2015


1. Introduction
I discuss in this paper results which arise in some materials as a consequence of particle-particle collisions. When two particles in a material collide, the energy and linear momentum are conserved. The total of the energy and linear momentum of the particles before and after the collision therefore remains unchanged. Within the laws of statistical mechanics such collisions increase the entropy and are responsible for preserving the most probable distribution for the particles over the microstates of the system. For the purposes of this paper, I will consider two examples: example one consists of molecules in a fluid such as water which is kept in a container. All sides of the container are insulated against heat exchanges except one side which is exposed to the outside environment. The second example is composed of electrons in the conduction band of an ionic semiconductor. The wide gap Nitrides are particularly suitable for the purposes of this paper. I will show that particle-particle collision in example one is responsible for the cooling of the liquid by a process known as “evaporation”. In the second example I will demonstrate that electron in the ionic semiconductor could also cool down from its thermal equilibrium value when subjected to a strong electric field. Energy and momentum are two independent thermodynamic quantities but they are different in character. The main difference between them is that the momentum is a vector quantity and an energy scalar. In spite of this fundamental difference, I have shown in this paper that the process of randomization of these two quantities, under external forces, produces a common result of material “cooling”. There are not any papers discussing specifically this common property. The result in example one [1] is well known which discusses cooling of water as a result of randomization of energy during evaporation. The result in example two [2] arises from momentum randomization in ionic semiconductors when subjected to strong electric field.
2. State of the Particles
The distribution of water molecules in thermal equilibrium in example one and of electrons in example two is given by Maxwell-Boltzmann’s distribution [3] which provides the number of particles (molecules or conduction electrons) 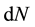 in small velocity ranges
in small velocity ranges 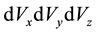 given by
given by
 (1)
(1)
where 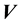 is the particle velocity and
is the particle velocity and 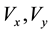 and
and  are the three components of the velocity in the x, y and z directions. Using the distribution (1) the average value of
are the three components of the velocity in the x, y and z directions. Using the distribution (1) the average value of 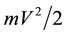 is given by
is given by 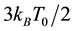 where
where  is the Boltzmann’s constant and
is the Boltzmann’s constant and 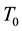 is the temperature of the molecules or of the electrons depending of the system used. If the distribution is disturbed by external forces a new distribution is established by the combined effects of the external forces and the electron-electron collisions. If the rate of collisions between the particles is faster than the rate of collisions of the electrons with the other external forces, the new distribution would assume the form:
is the temperature of the molecules or of the electrons depending of the system used. If the distribution is disturbed by external forces a new distribution is established by the combined effects of the external forces and the electron-electron collisions. If the rate of collisions between the particles is faster than the rate of collisions of the electrons with the other external forces, the new distribution would assume the form:
 (2)
(2)
The distribution given by (2) is called the “displaced Maxwell Boltzmann’s distribution” and was first proposed by H. Frohlich and Paranjape for conduction electrons when a semiconductor is subjected to a strong electric field [4] . In Equation (2),  is the displacement of electrons in the momentum space produced by the acceleration of electrons by the electric field and
is the displacement of electrons in the momentum space produced by the acceleration of electrons by the electric field and 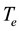 is the electron temperature which is different from the electron temperature at its equilibrium value
is the electron temperature which is different from the electron temperature at its equilibrium value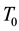 . The distribution (2) is the direct consequence energy momentum conserving collisions. Both
. The distribution (2) is the direct consequence energy momentum conserving collisions. Both 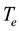 and
and ![]() are determined by the balancing of the input and output of the energy and the momentum by all the forces operating on the electron gas.
are determined by the balancing of the input and output of the energy and the momentum by all the forces operating on the electron gas.
There are different ways of obtaining the electron distribution function when it is under a strong electric field. One method is by expanding the distribution function in Legendre series and solving each term of the series by using the Boltzmann’s transport equation. This is a difficult and tedious method with the added limitation that one does not know how many terms in the series are needed for a realist approximation to the distribution function for a given electric field. The most popular method is the numerical evaluation of distribution function by
Monte Carlo
’s procedure. The procedure is effective for a small number of electrons say of the order of 100/cc. Any number beyond this would need the computer capacity for beyond the capacities of present day computers. We may have to wait a long time for the arrival of the quantum computers for use of
Monte Carlo
calculations when a large number of electrons are considered. Someone may ask “Do we need a large number of electrons or can the small number give realistic result for the distribution unction?” Unfortunately we need a large number of electrons if the randomization is to be achieved within a short time. Both these methods are not specific for solving the effect of a strong electric field. Use of Druvystein distribution may appear useful as it is in specific suited when high electric field is imposed. But the method is suited when the collisions occur between electrons and heavy atomic ions, a situation not applicable to my calculation. The displaced Maxwell distribution function, which I use, is particularly suited for obtaining the distribution function under strong electric field. The electron temperature and electron drift velocity, which I try to calculate appear as parameters in the distribution function and therefore they can be easily evaluated.
3. Evaporation of Liquid
Let us now consider example “one” which we introduced earlier in this paper. Water is stored in a container which is insulated on all sides except one of its side. The exposed side is in contact with the external environment which is kept dry and therefore practically free of water vapor. The energy distribution at temperature ![]() given by (1) indicates that there exits water molecules with a wide range of kinetic energies. Finite number of the molecules, however small the number might be, will have energy greater than the energy required to escape from the liquid. The escape energy is the energy by which the water in the container binds the molecule. Such molecules if near the water surface are capable of breaking out of the exposed of water surface and escape into the surrounding environment. The loss of energetic molecules by this process can occur continuously as long as the energetic molecules are present near the surface of the liquid and the external environment is sufficiently dry. The crossing of the energy barrier by the molecules should not to be confused with quantum tunneling. In evaporation, the water molecules possess sufficient energy to physically cross the potential barrier while in quantum tunneling the molecules may cross the barrier even when they have energy less than the potential barrier. The quantum tunneling is similar to a train crossing a mountain. In evaporation, the molecule has enough energy to overcome the barrier and is similar to a climber crossing the mountain. Evaporation must also be distinguished from the boiling of the liquid. Boiling occurs when the liquid reaches the boiling temperature. The evaporation takes place at all temperatures. The term “evaporation” is normally used when the liquid is below the boiling temperature. During evaporation, the liquid will gradually lose the high energy molecules and the low energy molecules which are unable to escape are left behind in the liquid. Thus the energy contents of the remaining liquid will gradually decrease. If the evaporation is allowed to continue for a long time then, in principle, the liquid will lose all energetic molecules and the evaporation will terminate. Such stoppage of the evaporation process would not occur as a consequence of particle-particle collisions. The high energy states lost during evaporation would be filled by molecules generated by the energy conserving molecule-molecule collisions in which two low energy molecules can collide to produce one molecule with sufficiently high energy and the other molecule returning to a lower energy state. Molecular collisions will also redistribute the energy of the remaining molecules to produce a reduction in temperature. The evaporation process would continue as long as there exists a supply of energetic molecules through particle-particle collisions. Higher the temperature faster is the evaporation. Often the evaporated molecules will remain in the vicinity of the surface and return to the liquid by a process which is converse of evaporation. The reverse process will bring back energetic molecules into the liquid and cause an increase in the temperature. Such heating can be prevented significantly by artificially blowing the energetic molecules away from the surface.
given by (1) indicates that there exits water molecules with a wide range of kinetic energies. Finite number of the molecules, however small the number might be, will have energy greater than the energy required to escape from the liquid. The escape energy is the energy by which the water in the container binds the molecule. Such molecules if near the water surface are capable of breaking out of the exposed of water surface and escape into the surrounding environment. The loss of energetic molecules by this process can occur continuously as long as the energetic molecules are present near the surface of the liquid and the external environment is sufficiently dry. The crossing of the energy barrier by the molecules should not to be confused with quantum tunneling. In evaporation, the water molecules possess sufficient energy to physically cross the potential barrier while in quantum tunneling the molecules may cross the barrier even when they have energy less than the potential barrier. The quantum tunneling is similar to a train crossing a mountain. In evaporation, the molecule has enough energy to overcome the barrier and is similar to a climber crossing the mountain. Evaporation must also be distinguished from the boiling of the liquid. Boiling occurs when the liquid reaches the boiling temperature. The evaporation takes place at all temperatures. The term “evaporation” is normally used when the liquid is below the boiling temperature. During evaporation, the liquid will gradually lose the high energy molecules and the low energy molecules which are unable to escape are left behind in the liquid. Thus the energy contents of the remaining liquid will gradually decrease. If the evaporation is allowed to continue for a long time then, in principle, the liquid will lose all energetic molecules and the evaporation will terminate. Such stoppage of the evaporation process would not occur as a consequence of particle-particle collisions. The high energy states lost during evaporation would be filled by molecules generated by the energy conserving molecule-molecule collisions in which two low energy molecules can collide to produce one molecule with sufficiently high energy and the other molecule returning to a lower energy state. Molecular collisions will also redistribute the energy of the remaining molecules to produce a reduction in temperature. The evaporation process would continue as long as there exists a supply of energetic molecules through particle-particle collisions. Higher the temperature faster is the evaporation. Often the evaporated molecules will remain in the vicinity of the surface and return to the liquid by a process which is converse of evaporation. The reverse process will bring back energetic molecules into the liquid and cause an increase in the temperature. Such heating can be prevented significantly by artificially blowing the energetic molecules away from the surface.
We have at some stage in life have experienced the cooling discussed above when we rub alcohol on the skin. The cooling of the skin is exactly for the same reason as the cooling we have mentioned in example one. The cooling of water by the process of evaporation was used in ancient times by utilizing porous vats for water storage. Porosity of the pots helped to enhance the effective surface area exposed to the environment and as a consequence generated increased evaporation. The vats were kept in airy surroundings. This is the most practical and inexpensive way to cool water for those who did not have access to refrigerators and for those who like hiking in deserts.
4. Ionic Semiconductors in High Electric Fields
The “second” example, as mentioned earlier in this paper, consists of an assembly of electrons in the conduction band of an ionic semiconductor. The energy distribution of electrons for a non-degenerate, n-type semiconductor is given by Maxwell-Boltzmann’s distribution (1). The temperature, a factor embedded in the distribution function, defines the equilibrium temperature of the electrons. If I disturb the system by an intense external D.C. electric field, the particle distribution will assume a new form. The changes depend on the degree of the external disturbance. According to Frohlich and Paranjape [4] , the distribution of electrons will assume the form (2) provided the rate of energy and momentum exchanges between electron-electron exceeds the energy and momentum exchange between the electrons and the ionic vibrations of the lattice.
For a n-type ionic semiconductor I have selected AlN because as a wide gap semiconductor it can sustain high electric fields without the occurrence of electrical breakdown. Let the vibrational frequency of the AlN lattice be ![]() which I assume for simplicity to be constant and therefore without dispersion. I will now discuss the changes in the state of the electrons by the combined effects of a high external field of magnitude several kilovolts per cm, of electron-phonon interaction and of electron-electron collisions. The electric field would accelerate each electron and impart linear momentum
which I assume for simplicity to be constant and therefore without dispersion. I will now discuss the changes in the state of the electrons by the combined effects of a high external field of magnitude several kilovolts per cm, of electron-phonon interaction and of electron-electron collisions. The electric field would accelerate each electron and impart linear momentum ![]() per second in the x-direction where -e is the charge of the electron and F is the electric field directed in the negative x-direction. The effect of the electron-phonon interaction on the state of the electrons depends on the kinetic energies E of the electrons. I will name the electrons with kinetic energy
per second in the x-direction where -e is the charge of the electron and F is the electric field directed in the negative x-direction. The effect of the electron-phonon interaction on the state of the electrons depends on the kinetic energies E of the electrons. I will name the electrons with kinetic energy ![]() as low energy electrons and electrons with
as low energy electrons and electrons with ![]() as high energy. The low energy electrons possess insufficient energy to emit an ionic phonon but they can absorb a phonon. The probability of phonon absorption is proportional to the phonon excitation number
as high energy. The low energy electrons possess insufficient energy to emit an ionic phonon but they can absorb a phonon. The probability of phonon absorption is proportional to the phonon excitation number ![]() given by the Planck distribu-
given by the Planck distribu-
tion![]() , where q is the wave vector of the phonon mode. The interaction of the low energy
, where q is the wave vector of the phonon mode. The interaction of the low energy
electrons with the ionic lattice is minimal as they cannot emit a phonon and have low probability of phonon absorption when the temperature is lower than the phonon frequency. The low energy electrons will propagate under the action of the D.C. field without much hindrance from the electron-phonons interaction and therefore gather large linear momentum. Lower the temperature, higher is the momentum acquisition. In fact by increasing the electric field, there is no theoretical limit to the linear momentum that low energy electrons can acquire. The situation with the high energy electrons is considerably different. These electrons can emit as well as absorb phonons. The probability of phonon emission is as stated earlier proportional to ![]() which attains a constant value of unity as the temperature is lowered. The contrast between the momentum acquisitions by the low and high energy electrons is substantially large. The low energy electrons can acquire a large amount of linear momentum while the high energy electrons acquire relatively much smaller amount. We now add the effect of momentum conserving electron-electron collisions which is the main aim of this paper. These collisions tend to equalize the momentum and reduce the disparity in momentum acquisition between high and low energy electrons. This role is evident from Equation (2) where conduction electrons under the electron-electron collisions attain a constant linear momentum of value
which attains a constant value of unity as the temperature is lowered. The contrast between the momentum acquisitions by the low and high energy electrons is substantially large. The low energy electrons can acquire a large amount of linear momentum while the high energy electrons acquire relatively much smaller amount. We now add the effect of momentum conserving electron-electron collisions which is the main aim of this paper. These collisions tend to equalize the momentum and reduce the disparity in momentum acquisition between high and low energy electrons. This role is evident from Equation (2) where conduction electrons under the electron-electron collisions attain a constant linear momentum of value ![]() which is average momentum of the entire electron gas. The action of the electron-electron collisions must lead to a flow of linear momentum from low to high energy electrons causing a further reduction in linear momentum in low energy electrons and increase of linear momentum of the high energy electrons.
which is average momentum of the entire electron gas. The action of the electron-electron collisions must lead to a flow of linear momentum from low to high energy electrons causing a further reduction in linear momentum in low energy electrons and increase of linear momentum of the high energy electrons.
5. Conclusion
I now turn my attention to thermal energy contents of the conduction electrons. The thermal energy of the electrons is determined by the difference in rates at which the conduction electrons acquire and lose thermal energy. The low energy electrons can only gain energy from the lattice by the absorption of the phonons while the high energy electrons can mainly lose energy. Both the rates also depend on the magnitude of linear momentum. The role of the electron-electron collisions is to balance the momentum between high and low energy electrons. Thus the energy loss by the high energy electrons is enhanced as they receive momentum from the electric field as well as momentum from the low energy electrons. The energy gain by the low energy electrons is reduced by electron-electron collisions. The enhancement of the energy loss and reduction of energy gain arise as a result of the electron-electron collisions. The difference between gain and loss of the thermal energy gives rise to the electron gas either “cooling” or “heating”. I have shown in this paper that the disparity in momentum arises when the electric filed is high. Although there are limits to the magnitudes of high electric fields that can be imposed, the significant cooling of electron temperature can occur in AlN in transient electric fields and in D.C. electric fields in the range of 100 - 150 kV. In this range, I have shown [2] that 10% decrease in electron temperature is possible when the equilibrium lattice temperature is 300˚K. For lower values of the electric field than the range prescribed above, the decrease in electron temperature is proportionately lower. The numerical evaluation of net flows of energies in the electron gas requires a detailed evaluation [2] , using methods of quantum and statistical mechanics. I have done these evaluations in a recent paper [2] and have demonstrated that cooling of electrons could occur in wide-gap Nitrides.