1. Introduction
Creating a simple, usable and reliable computing model of a complex mixture, such as NdFeB, is quite stubborn theoretically under high pressure and high temperature, but is really significant in aerospace engineering and defense industry [1] . In recent years, some of shock and FEM experimental data of NdFeB had been already published in lower pressure range [2] -[5] ; we have reached at the top of pressure, 78 GPa, experimentally so far, and the satisfactory result will allow us confidently to predict the characteristics of NdFeB in a higher pressure region.
For the sake of simplifying our calculation, the anisotropic Nd2Fe14B was chosen, because of its principle application in modern society with its high magnetic energy product, remanence ratios and coercive force, and we ignored the existence of B in the model.
2. Methods
2.1. Gruneisen’s Model
Based on the shock experimental inertia of Nd2Fe14B within 18 GPa - 78 GPa [3] , as a linear mixed substance, it is suitable for calculating [6] by
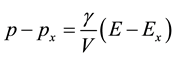 (1)
(1)
where P, V, E, g, Px and Ex are, respectively, total pressure, volume, energy, Gruneisen’s coefficient, cold pressure and energy. Among of them, Px and Ex can be specifically represented by the Born-Meyer’s potential [6] ,
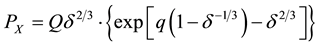 (2)
(2)
 (3)
(3)
where Q, q, r0 and av are, respectively, the parameters of cold energy, the initial density and the volume dilatation, d = r/r0k and r0k = r0 (1 + 300 an).
2.2. Volume Superposition Principle
Instead of computing this intermetallic compound, each component, Nd, Fe and B will be allowed to be treated separately, according to their proportion by weight, 26.68%, 72.32% and 0.99% due to the chemical stability of the compound under high pressure and high temperature, as mentioned above. The average formulae are listed below,
 (4)
(4)
 (5)
(5)
where ai denotes weight percentage of each component.
2.3. Hugoniot’s Relation
The interaction of particles in Nd2Fe14B will be ignored if the compound is actually treated as an ideal mixture. The compressibility of Nd2Fe14B, therefore, can be evaluated by the Hugoniot of each component itself [6] , as follows,
 (6)
(6)
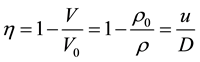 (7)
(7)
where c0 and l0 are, respectively, the wave velocity and the characteristic parameter of Nd2Fe14B. At the initial state, they are,
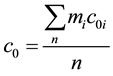 (8)
(8)
 (9)
(9)
where mi stands for the mass of each independent component in mixture. Sequentially, we take c0 = 3.686 and λ0 = 1.059, at the same pressures in literature [6] . Then we can get Q » 55.7 and q » 6.85 by the following formulae [6] ,
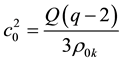 (10)
(10)
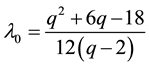 (11)
(11)
It must be emphasized that c0 and λ0 in Equations (8)-(11) should be demarcated to the absolute zero from the room temperature in calculation by the linear mixed rule [3] .
 (12)
(12)
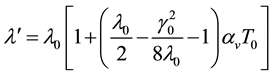 (13)
(13)
where g0 is the initial Grunasen’s coefficient of Nd2Fe14B, which is taken as 1.492, and ρ0k as 7.451 g/cm3 [3] . While the boron has to be erased from processing queue due to lack of its Hugoniot and trivial weight, which is also reasonable in common senses.
2.4. Shear Modulus
The effective shear modulus, G, can be deduced from the SCG model [7] , based on the quasi-elasticity as unloading along with the shock adiabat [6] , as follows,
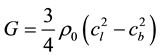 (14)
(14)
where cl and cb are, respectively, the Euler’s longitudinal and bulk wave velocity, and given by,
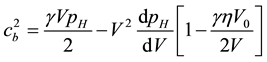 (15)
(15)
 (16)
(16)
![]() (17)
(17)
where n, the Poisson’s ratio, is taken as 0.24, and g is supposed to depend on volume V only. Then we have,
![]() (18)
(18)
where r is density at final state, and a = 0.822 nm is the lattice constant of Nd2Fe14B.
For convenience reasons in the following calculation and discussion, part of initial parameters of Nd and Fe are listed in Table 1.
Compare with prior experiments, the calculated results have been listed in Table 2.
3. Results and Discussion
By using Equations (1)-(16), a new D-u relation, D = 3.476 + 1.203 u, of Nd2Fe14B can be obtained, as shown in Figure 1 together with a series of experiments and literature data of Nd and Fe. It is apparently, these points are well fitted between species with a deviation of ±0.125% throughout the given pressures range, and the result, the D-u line located between lines of Nd and Fe, and more closed to the latter, is just because of the volume superposition principle. That is, the pressure properties of linear mixtures will strongly depend on their components’ volume or weight, if only their inertia being kept during loading process. Therefore, the same distribution can be seen on a corresponding group of adiabats P vs. V of Figure 2, which are fitted by polynomial with standard deviation of ±2.30% as loading Nd2Fe14B up to 140 GPa.
Considering the accordance between calculations and experiments below 78 GPa in Figure 1 and Figure 2,
![]()
Table 1. Part of initial parameters of Nd and Fe.
![]()
Table 2. Comparison of calculations vs. experiments.
*Cited from literature [3] .
![]()
Figure 1. Theoretical D-u vs. experimental one of Nd2Fe14B.
![]()
Figure 2. Theoretical adiabat vs. experimental one of Nd2Fe14B.
![]()
Figure 3. Euler’s bulk and longitudinal wave velocity and the Shear modulus vs. axial stress of Nd2Fe14B.
the segments are also reasonable from 78 GPa to 140 GPa based on the prior assumption of the stability chemically as loading pressure on Nd2Fe14B.
On the basis of above discussion, the longitudinal, bulk wave velocities and the shear modulus of Nd2Fe14B can be estimated by Equations (14)-(18) as shown together in Figure 3. A pair of quasi-parallel curves and a monotonous line very distinctly proved that the organization inside Nd2Fe14B were unchanged with such rising pressure, which meant no shock softening meanwhile, or no melting occurred from the lowest to the highest pressure region once again.
4. Conclusions
A simple and effective algorithm for evaluating Nd2Fe14B has been developed via comparing experiments below 78 GPa and predicted towards 140 GPa together with the shear modulus, even no corresponded experimental data accompanied. We believe the deviation in calculation can be further reduced by carefully adjusting parameters in the equations listed above; and the processing method can be consequentially extended to other inert mixtures under high pressure and high temperature. But two rules should be followed:
1) Each component of solid mixture should be inert during shock compression, and
2) Each initial parameter of components should be known in advance.