The Introduction of Specific Water and Maximum Airborne Specific Water & the Improvement of Dynamic Equations on Non-Uniform Saturated Moist Atmosphere ()
1. Introduction
Due to the important roles of water vapor in the genesis and development of weather systems, many studies have contributed to the dynamical discussion on moist atmosphere, e.g., Betts A. K., (1973) [1] ; Xie Y. B., (1978) [2] ; Wang L. M., (1980) [3] [4] ; Tripoli G. J., W. R. Cotton, (1981) [5] ; Pointin Y., (1984) [6] ; Hauf T., H. Holler, (1987) [7] ; Ooyama K. V., (1990) [8] ; (2000) [9] ; Persson O., (1995) [10] ; Wu G. X., Y. P. Cai and X. J. Tang, (1995) [11] ; Soriano L. J., E. L. Diez, (1997) [12] ; Schubert W. H., S. A. Hausman, and M. Garcia et al., (2001) [13] ; Bannon P. R., (2002) [14] .
To consider the transitional area between the unsaturated and saturated atmosphere, the discontinuity could occur in the latent heat term of the thermodynamic equation when the latent heat is released in the saturated atmosphere whereas latent heat is not released in the unsaturated atmosphere. Traditionally, the discontinuity in the latent heat term of the thermodynamic equation can be summarized by the Dirac delta function. The discontinuity makes the theoretical analysis very difficult for near saturated atmosphere, where the relative humidity is usually large enough to condensate but not saturated (just like rain regions), so these discussions are limit to the condition of saturated atmosphere e.g., Wang L. M., (1980) [3] [4] ; Wu G. X., Y. P. Cai and X. J. Tang, (1995) [11] , (realistic atmosphere is non-uniform saturated), or limit to the condition of equilibrium airflow, e.g., Ooyama K.V., (1990) [8] ; (2000) [9] ; Schubert W.H., S.A. Hausman, and M. Garcia et al., (2001) [13] , (realistic airflow is not always equilibrium).
However, the condensation process does not occur so abruptly in realistic atmosphere. According to the observational evidences pointed by Mason, (1971) [15] , the condensation process might occur at 78% of relative humidity under the condition of the appropriate condensation nuclear in real atmosphere. Therefore, a condensation probability function 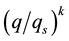 is introduced by Wang X. R. and K. J. Wu, (1995) [16] , Wang X. R., C. E. Chi and Z. X. Wang, (1997) [17] and Wang X. R., Z. X. Wang, and C. N. Shi, (1999) [18] , which is expected to represent the continuity of this kind of variation, here
is introduced by Wang X. R. and K. J. Wu, (1995) [16] , Wang X. R., C. E. Chi and Z. X. Wang, (1997) [17] and Wang X. R., Z. X. Wang, and C. N. Shi, (1999) [18] , which is expected to represent the continuity of this kind of variation, here 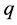 and
and 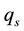 are the specific humidity and saturated specific humidity respectively,
are the specific humidity and saturated specific humidity respectively, 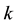 is a function of pressure, temperature, specific humidity and the density of condensation cores. When
is a function of pressure, temperature, specific humidity and the density of condensation cores. When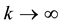 , the function is degraded to the Heaviside step function. Thus, the condensation probability function is a generalized Heaviside step function, which leads to the continuity of the latent heat term of the thermodynamic equation in the transition area between the unsaturated and saturated air. They constituted a more approximate thermodynamic equation for the saturated and/or near saturated atmosphere, where the relative humidity is usually large enough to condensate but not saturated (just like rain regions). Based on the fact that condensation occurs when
, the function is degraded to the Heaviside step function. Thus, the condensation probability function is a generalized Heaviside step function, which leads to the continuity of the latent heat term of the thermodynamic equation in the transition area between the unsaturated and saturated air. They constituted a more approximate thermodynamic equation for the saturated and/or near saturated atmosphere, where the relative humidity is usually large enough to condensate but not saturated (just like rain regions). Based on the fact that condensation occurs when 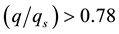 in the real atmosphere due to the existence of condensation cores, and by theoretical analysis and numerical simulation, Wang X. R., Z. X. Wang, and C. N. Shi, (1999) [18] , found when k is about 9, the condensation in the atmosphere is represented well. And hence, we specify
in the real atmosphere due to the existence of condensation cores, and by theoretical analysis and numerical simulation, Wang X. R., Z. X. Wang, and C. N. Shi, (1999) [18] , found when k is about 9, the condensation in the atmosphere is represented well. And hence, we specify 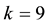 in our study. Following this discussion, the dynamic equations on non-uniform saturated moist atmosphere (EQSNUSMA) are provided.
in our study. Following this discussion, the dynamic equations on non-uniform saturated moist atmosphere (EQSNUSMA) are provided.
On the basis of EQSNUSMA, a battery of results is got:
Wang X. R. and K. J. Wu, (1995) [16] , found that the direction of geo-strophic equilibrium wind of moist air is parallel to equipotential line, its wind speed is equal to the product of dry air geo-strophic equilibrium wind
speed and static non-equilibrium parameter . The wind speed of geo-strophic
. The wind speed of geo-strophic
equilibrium wind of moist air is less than that of dry air, because static non-equilibrium parameter is less than 1. It was pointed out that the super-geo-strophic behavior of low level jet streams is caused by non-equilibrium relating to jet strengthening, it is not equilibrium airflow.
The non-uniform saturated moist potential vorticity (NUSMPV), or the generalized moist potential vorticity (GMPV), is thus defined and its tendency equation is derived by Wang X. R., Z. X. Wang and C. N. Shi, (1998) [19] ; Gao S. T., X. R. Wang and Y. S. Zhou, (2004) [20] ; Wang X. R. and M Wei, (2007) [21] . The analysis shows that in a frictionless and moist adiabatic flow, the NUSMPV, (or GMPV), can be generated in the unsaturated air only and its generation rate is determined by the environmental moisture and its gradient. It is further shown that in the sub-saturated regions![]() , the NUSMPV is not conserved; whereas, in the other unsaturated regions, the NUSMPV may be nearly conserved.
, the NUSMPV is not conserved; whereas, in the other unsaturated regions, the NUSMPV may be nearly conserved.
Based on the works by Wang X. R., Z. X. Wang and C. N. Shi, (1998) [19] ; Wang X. R., X. P. Chen and S. P. Xun, (1998) [22] ; Wang X. R., K. J. Wu and X. P. Chen et al., (1999) [23] and Wang X. R., Z. X. Wang, and C. N. Shi, (1999) [18] , the transformation mechanism between weather systems of different scale is discussed by Wang X. R., M. Wei, (2007) [21] . According to the relativity principle of conservation, by discussing the non-dimensional form of the NUSMPV equation, the atmospheric motion is classified into three types: motions with conserved, quasi-conserved, and non-conserved NUSMPV. It is pointed out as follows. When the dynamic non-equilibrium degree ![]() decreases so that the condition of NUSMPV conservation is satisfied, the atmospheric motion in NUSMPV conservation state transforms from smaller scale to larger scale mainly by the very fast adaptation process (A is solenoidal term, B is diabetic heating, P0 is narrow sense NUSMPV.). In this kind of process the non-equilibrium energy is dispersed and lost by gravitational and sound wave. On the contrary, when the
decreases so that the condition of NUSMPV conservation is satisfied, the atmospheric motion in NUSMPV conservation state transforms from smaller scale to larger scale mainly by the very fast adaptation process (A is solenoidal term, B is diabetic heating, P0 is narrow sense NUSMPV.). In this kind of process the non-equilibrium energy is dispersed and lost by gravitational and sound wave. On the contrary, when the ![]() increases so that the condition of non-conservation is satisfied, the atmospheric motion in the NUSMPV non-conservation state transforms from larger scale to smaller scale mainly by the very fast excitation process. In this kind of process the (A + B) changes NUSMPV by changing vorticity and
increases so that the condition of non-conservation is satisfied, the atmospheric motion in the NUSMPV non-conservation state transforms from larger scale to smaller scale mainly by the very fast excitation process. In this kind of process the (A + B) changes NUSMPV by changing vorticity and![]() . Either of the two kinds of transformation process mentioned above will constantly go along till the atmospheric motion is back in the state of NUSMPV quasi-conservation. From the transformation mechanism between weather systems of different scale, according to the basal characteristic of the sudden heavy rain in mid-latitude (SHR), by discussing the condition of NUSMPV non-conservation, the four necessary occurrence conditions of SHR are proved theoretically by Wang X. R., Y. Y. Zheng and S. T. Gao et al., (2006) [24] . By the analysis of the Doppler radar and cloud chart data related to two courses of the SHR in Hefei city in 1999, it is known that, just before occurrence of SHR, both courses have two common possible premonitory characters embodying the four necessary conditions.
. Either of the two kinds of transformation process mentioned above will constantly go along till the atmospheric motion is back in the state of NUSMPV quasi-conservation. From the transformation mechanism between weather systems of different scale, according to the basal characteristic of the sudden heavy rain in mid-latitude (SHR), by discussing the condition of NUSMPV non-conservation, the four necessary occurrence conditions of SHR are proved theoretically by Wang X. R., Y. Y. Zheng and S. T. Gao et al., (2006) [24] . By the analysis of the Doppler radar and cloud chart data related to two courses of the SHR in Hefei city in 1999, it is known that, just before occurrence of SHR, both courses have two common possible premonitory characters embodying the four necessary conditions.
Furthermore, in recent years, some new variables from EQSNUSMA, such as generalized potential temperature, GMPV, generalized convective vorticity vector et al., are applied more to the dynamical analysis of hot and humid weather systems and torrential rain systems, e.g., Gao S. T., Y. S. Zhou, T. Lei et al. (2005) [25] ; Sheng S. Q. and Y. S. Zhou, (2007) [26] ; Yang S., S. T. Gao, D. H. Wang, (2007) [27] ; Zhou Y. S., J. Cao and D. H. Wang. (2007) [28] ; Duan T. Y., G. Deng. and D. H. Wang, (2007) [29] ; Gao S. T. and C. G. Cui, (2007) [30] ; Cao J. and S. T. Gao, (2008) [31] ; Zhou Y. S., (2009) [32] ; Zhaoming Liang, Chungu Lu and Edward I. Tollerud, (2010) [33] ; Zhou Y. S. and K. F. Zhu. (2010) [34] .
Such great progress for dynamic on non-uniform saturated moist atmosphere has been made in theory and application aspects, but, in all studies, almost no one is involved in the discussion on condensed liquid water. Traditionally, it is supposed that condensed liquid water always precipitates immediately. However, it is not true, in realistic atmosphere, the condensed liquid water either falls down in the form of precipitate or is detained in the air in the form of airborne liquid water (fog or cloud). By the analysis of some failure model experiments on dynamic equations on non-uniform saturated moist atmosphere, it is found that the reason of failure is exactly the irrational supposition that condensed liquid water always falls down immediately. So, in the dynamic equations on non-uniform saturated moist atmosphere, it becomes a question how to consider the condensed liquid water in air. By the discussion of airborne liquid water content and the balance equation between water vapor and liquid water, the new idea (not only precipitate contains condensed liquid water also includes airborne liquid water) is firstly raised and an advanced precipitable formula is set up by Wang, X.R., Gao, S.T. (2007) [35] . But the paper is not involved in the discussion on the condition, under which condensed liquid water can precipitate only, otherwise it is detained in the air and becomes airborne liquid water. And that, in the paper, the deduction in p coordinate is not correct, so the airborne coefficient estimated is also an inaccuracy.
To eliminate the irrational supposition that condensed liquid water always falls down immediately, specific water m and maximum airborne specific water ![]() is introduced into the dynamic framework to derive the balance equation between water vapor and airborne liquid water and a new formula of precipitate rate in Section 2. Following above discussion, improved dynamic equations on non-uniform saturated moist atmosphere are provided in Section 3. From the data provided by the leading group for studying the super-heavy rain in Henan in China in August 4-8 1975 [LGSHR1975] (1977), airborne coefficient is roughly estimated in Section 4. The summary is given in Section 5.
is introduced into the dynamic framework to derive the balance equation between water vapor and airborne liquid water and a new formula of precipitate rate in Section 2. Following above discussion, improved dynamic equations on non-uniform saturated moist atmosphere are provided in Section 3. From the data provided by the leading group for studying the super-heavy rain in Henan in China in August 4-8 1975 [LGSHR1975] (1977), airborne coefficient is roughly estimated in Section 4. The summary is given in Section 5.
2. The Balance Equation between Water Vapor and Airborne Liquid Water
2.1. The Discussion in the Condition of w ³ 0
In the condition of ![]() (w is the vertical velocity in z coordinate), if the water vapor condenses, the condensed liquid water falls down in the form of precipitate or is detained in the air in the form of airborne liquid water (fog or cloud). Because of the resistance of up-current, if condensed liquid water does not gain enough mass, (larger water droplets overcoming up-current resistance are not able to occur,) it is detained in the air in the form of airborne liquid water. If it gains enough mass, (larger water droplets overcoming up-current resistance are able to occur,) the liquid water mass over the maximum airborne liquid water mass detained by up-current falls down in the form of precipitate.
(w is the vertical velocity in z coordinate), if the water vapor condenses, the condensed liquid water falls down in the form of precipitate or is detained in the air in the form of airborne liquid water (fog or cloud). Because of the resistance of up-current, if condensed liquid water does not gain enough mass, (larger water droplets overcoming up-current resistance are not able to occur,) it is detained in the air in the form of airborne liquid water. If it gains enough mass, (larger water droplets overcoming up-current resistance are able to occur,) the liquid water mass over the maximum airborne liquid water mass detained by up-current falls down in the form of precipitate.
Following Wang X. R., Z. X. Wang and C. N. Shi (1999) [18] , by introducing the condensation probability function ![]() to replace the Dirac delta function, the thermodynamic equation and the balance equation between water vapor and airborne liquid water may be respectively expressed as
to replace the Dirac delta function, the thermodynamic equation and the balance equation between water vapor and airborne liquid water may be respectively expressed as
![]() (1)
(1)
![]() (2)
(2)
where![]() ,
, ![]() is the diabatic heating excluding the latent heating, m is specific water (the ratio of the airborne liquid water mass to the moist air mass in unit cubage moist air),
is the diabatic heating excluding the latent heating, m is specific water (the ratio of the airborne liquid water mass to the moist air mass in unit cubage moist air), ![]() is maximum airborne specific water (the ratio of the maximum airborne liquid water mass detained by up-current to the moist air mass in unit cubage moist air),
is maximum airborne specific water (the ratio of the maximum airborne liquid water mass detained by up-current to the moist air mass in unit cubage moist air), ![]() is precipitate rate (the ratio of the liquid water mass over the maximum airborne liquid water mass to the moist air mass in unit cubage moist air), others are common symbols.
is precipitate rate (the ratio of the liquid water mass over the maximum airborne liquid water mass to the moist air mass in unit cubage moist air), others are common symbols.
Following Mason, (1971) [15] , ![]() may be expressed as
may be expressed as
![]() (3)
(3)
where ![]() is water density,
is water density, ![]() is air density,
is air density, ![]() is the number of liquid water droplets with radius r in unit cubage moist air. Following Levin, 1954 [36] ,
is the number of liquid water droplets with radius r in unit cubage moist air. Following Levin, 1954 [36] , ![]() may be expressed as
may be expressed as
![]() (4)
(4)
where N is the all number of liquid water droplets, ![]() is standard deviating,
is standard deviating, ![]() is geometrical mean radius (the radius of liquid water droplets with the highest probability. From Equation (4), we have
is geometrical mean radius (the radius of liquid water droplets with the highest probability. From Equation (4), we have
![]() (5)
(5)
According to the observational evidences pointed by Mason, (1971) [15] , Squires P. (1958) [37] , Warner J. (1955) [38] , Warner J. and T. D. Newnham, (1952) [39] and Weickmann H. K. and H. J. Aufm Kampe, (1953) [40] , The distribution of airborne liquid water mass in cloud is related to the distribution of vertical velocity. According to force equilibrium principle, in the condition of![]() , if the radius of liquid water droplets is smaller, liquid water droplets uptrend, on the contrary downtrend. So when
, if the radius of liquid water droplets is smaller, liquid water droplets uptrend, on the contrary downtrend. So when![]() , the liquid water droplet with
, the liquid water droplet with ![]() is in the state of equilibrium, its viscous resistance is equal to its gravity, so
is in the state of equilibrium, its viscous resistance is equal to its gravity, so
![]() . (6)
. (6)
where ![]() is coefficient of viscosity, g is acceleration of gravity,
is coefficient of viscosity, g is acceleration of gravity, ![]() is its velocity relative to up-current. Because it is in the state of equilibrium, so
is its velocity relative to up-current. Because it is in the state of equilibrium, so
![]() (7)
(7)
With Equation (5), (6) and (7), Equation (3) becomes
![]() (8)
(8)
![]() . (9)
. (9)
From the physical properties in cumuliform clouds versus height above cloud base (Figure 1) by Weickmann H. K. and H. J. Aufm Kampe, (1953) [40] , it may be found that, if the relation curve ![]() -h of the temperature at observation point (
-h of the temperature at observation point (![]() ) to the height above base (h) convert to the
) to the height above base (h) convert to the ![]() -h relation curve, it is very similar to the relation curve N-h of the number of cloud droplets in cumulus clouds (N) to h, in other words, N is roughly proportional to
-h relation curve, it is very similar to the relation curve N-h of the number of cloud droplets in cumulus clouds (N) to h, in other words, N is roughly proportional to![]() , so in saturated moist air,
, so in saturated moist air,
![]() (10)
(10)
here a is the coefficient independent of p and T. Because ![]() may be satisfied in saturated atmosphere only, with Equation (10), Equation (8) and (9) become:
may be satisfied in saturated atmosphere only, with Equation (10), Equation (8) and (9) become:
![]() (11)
(11)
![]() , (12)
, (12)
here ![]() is airborne coefficient. Strictly speaking, because
is airborne coefficient. Strictly speaking, because ![]() is a function of
is a function of ![]() and condensation nuclear, the character of
and condensation nuclear, the character of ![]() is not clear. Nothing but for simpleness, we specify
is not clear. Nothing but for simpleness, we specify ![]() (pending constant) in our study. Based on above discussion, with Equation (11), Equation (2) may be written as
(pending constant) in our study. Based on above discussion, with Equation (11), Equation (2) may be written as
![]() (13)
(13)
When liquid water precipitates, with Equation (13), a new formula of precipitate rate is got as
![]() (14)
(14)
From Equation (14), not only does precipitating liquid water contains condensed liquid water, but also contains converged and existing airborne liquid water.
In addition, Equation (14) can be rewritten as
![]()
Figure 1. The physical properties in cumuliform clouds versus height above cloud base.
![]() (15)
(15)
The generalized temperature ![]() is defined as
is defined as
![]() , (16)
, (16)
in saturated moist air (![]() ), Equation (15) can be rewritten as
), Equation (15) can be rewritten as
![]() . (17)
. (17)
In moist adiabatic condition, using thermodynamic equation, state equation and continuity,
![]() (18)
(18)
![]() (19)
(19)
![]() , (20)
, (20)
Equation (17) can be rewritten as
![]() (21)
(21)
In real atmosphere,
![]() (22)
(22)
![]() (23)
(23)
![]() (24)
(24)
From Equation (22), (23) and (24), we have
![]() (25)
(25)
In other words, ![]() is negligible in Equation (15), (17) and (21), Equation (15), (17) and (21) can
is negligible in Equation (15), (17) and (21), Equation (15), (17) and (21) can
be rewritten as
![]() (26)
(26)
![]() (27)
(27)
![]() (28)
(28)
2.2. The Discussion in the Condition of w < 0
In the condition of![]() , all liquid water always falls down immediately because of down-current, so
, all liquid water always falls down immediately because of down-current, so
![]() (29)
(29)
![]() (30)
(30)
With Equation (30), Equation (2) becomes
![]() (31)
(31)
From Equation (31), because![]() , so
, so
![]() (32)
(32)
In addition, because of down-current, the rising temperature cased by adiabatic expansion restrains condensation process, so
![]() (33)
(33)
From Equation (32) and (33), we have
![]() (34)
(34)
3. The Improved Dynamic Equations on Non-Uniform Saturated Moist Atmosphere
Following Wang X. R., Z. X. Wang and C. N. Shi (1999) [18] and above discussion, by introducing the con- densation probability function![]() , specific water m and maximum airborne specific water
, specific water m and maximum airborne specific water![]() , The im- proved dynamic equations on non-uniform saturated moist frictionless atmosphere in z coordinate may be provided as
, The im- proved dynamic equations on non-uniform saturated moist frictionless atmosphere in z coordinate may be provided as
![]() (35)
(35)
![]() (36)
(36)
![]() (37)
(37)
![]() (38)
(38)
![]() (39)
(39)
![]() (40)
(40)
![]() (41)
(41)
In moist adiabatic condition, from Equations (35)-(41) and the definition of generalized temperature ![]() (16), built upon the transform formula between
(16), built upon the transform formula between ![]() (in p coordinate) and w (in z coordinate)
(in p coordinate) and w (in z coordinate)
![]() (42)
(42)
and the vertical coordinate transform formula based on the non-static equilibrium by Wang X. R., C. E. Chi and Z. X. Wang (1997) [17] , the improved dynamic equations on non-uniform saturated moist frictionless and adiabatic atmosphere in p coordinate may be provided as
![]() (43)
(43)
![]() (44)
(44)
![]() (45)
(45)
![]() (46)
(46)
![]() (47)
(47)
![]() (48)
(48)
![]() (49)
(49)
From Equation (35)-(41) and (43)-(49), the dynamic equations on non-uniform saturated moist atmosphere are improved, because of introducing specific water m and maximum airborne specific water![]() , and eliminating the irrational supposition that condensed liquid water always falls immediately, and adding the balance equation between water vapor and airborne liquid water (40) or (48) and the new formula of precipitate rate (41) or (49). From Equation (40) or (48), in up-current (
, and eliminating the irrational supposition that condensed liquid water always falls immediately, and adding the balance equation between water vapor and airborne liquid water (40) or (48) and the new formula of precipitate rate (41) or (49). From Equation (40) or (48), in up-current (![]() ) or (
) or (![]() ), the condensed liquid water can precipitate under the condition with
), the condensed liquid water can precipitate under the condition with ![]() and
and ![]() or
or ![]() only, otherwise it is detained in the air and becomes airborne liquid water. From Equation (41) or (49), when liquid water precipitates, not only does precipitating liquid water contain condensed liquid water, but also contains converged and existing airborne liquid water.
only, otherwise it is detained in the air and becomes airborne liquid water. From Equation (41) or (49), when liquid water precipitates, not only does precipitating liquid water contain condensed liquid water, but also contains converged and existing airborne liquid water.
4. The Rough Estimation of Airborne Coefficient
Because the character of ![]() is not clear, its accurate calculation requires a large number of data and complex work, so it is to be discussed in another article on account of space relation. Here, it is supposed that
is not clear, its accurate calculation requires a large number of data and complex work, so it is to be discussed in another article on account of space relation. Here, it is supposed that ![]() is a constant (airborne coefficient
is a constant (airborne coefficient![]() ) only.
) only.
With the new formula of precipitate rate in p coordinate (49), the new formula of rainfall intensity can be written roughly as
![]() (50)
(50)
where ![]() is the new estimated value of rainfall intensity (containing condensed liquid water and converged existing airborne liquid water),
is the new estimated value of rainfall intensity (containing condensed liquid water and converged existing airborne liquid water), ![]() is the height of cloud base,
is the height of cloud base, ![]() is the height of cloud top.
is the height of cloud top.
When estimating rainfall intensity, it is usually assumed that the local change of meteorological equal to 0, so
![]() (51)
(51)
If assuming ![]() as a quadratic function and considering
as a quadratic function and considering![]() , then, according Zhang et al., (1990) [41] , from (50) and (51), there is:
, then, according Zhang et al., (1990) [41] , from (50) and (51), there is:
![]() (52)
(52)
where ![]() is the estimated value by the conventional rainfall intensity formula, it may be expressed as
is the estimated value by the conventional rainfall intensity formula, it may be expressed as
![]() (53)
(53)
here
![]() . (54)
. (54)
where Fc is the confluent function of airborne liquid water, it may be expressed as
![]() (55)
(55)
![]() (56)
(56)
![]() (57)
(57)
![]() (58)
(58)
On the theoretical plane, using the synchronous analysis data with rainfall provided by RAFS (regional analysis and forecasting system), let the actual rainfall intensity![]() , the
, the ![]() could be calculated from (52-58), but, in fact, it is very difficult, because, the error of
could be calculated from (52-58), but, in fact, it is very difficult, because, the error of ![]() and
and ![]() (caused by the restrictions of observation systems) is so big that, the error of estimated
(caused by the restrictions of observation systems) is so big that, the error of estimated ![]() is also big, and it amounts to or exceed
is also big, and it amounts to or exceed ![]() frequently, and sometimes
frequently, and sometimes![]() . Only when the actual rainfall intensity is strong enough before
. Only when the actual rainfall intensity is strong enough before ![]() can be estimated.
can be estimated.
Here, in the supposition that ![]() is a constant (airborne coefficient
is a constant (airborne coefficient![]() ) only, using the data provided by the leading group for studying the super-heavy rain in Henan in China in August 4-8 1975 [LGSHR1975], (1977) [42] ,
) only, using the data provided by the leading group for studying the super-heavy rain in Henan in China in August 4-8 1975 [LGSHR1975], (1977) [42] , ![]() is estimated roughly.
is estimated roughly.
The gross-precipitation of this super-heavy rain is 1631.1mm, the maximum rainfall intensity is 189.5 mm/h (in the neighborhood of Banqiao reservoir in August 7, 22:00 Beijing time), in August 7, 20:00 Beijing time (the observation time on schedule), the center rainfall intensity on large scale surface weather chart is 12.5 mm/h, the actual extremes of rainfall intensity is 99.7 mm/h (in the neighborhood of Banqiao reservoir). Although the horizontal distribution graph of ![]() (the rainfall intensity estimated by the traditional formula of precipitate rate) is very similar to actual distribution graph (figures not shown), the center value of
(the rainfall intensity estimated by the traditional formula of precipitate rate) is very similar to actual distribution graph (figures not shown), the center value of ![]() is 7.7 mm/h, which is much less than actual center value 12.5 mm/h not mentioning the actual extremes of rainfall intensity 99.7 mm/h.
is 7.7 mm/h, which is much less than actual center value 12.5 mm/h not mentioning the actual extremes of rainfall intensity 99.7 mm/h.
With the new formula of precipitate rate in p coordinate (49), using mean value theorem, the new formula of rainfall intensity can be written roughly as
![]() (59)
(59)
where ![]() is the new estimated value of rainfall intensity (containing condensed liquid water and converged existing airborne liquid water),
is the new estimated value of rainfall intensity (containing condensed liquid water and converged existing airborne liquid water), ![]() is the height of cloud base,
is the height of cloud base, ![]() is the height of cloud top,
is the height of cloud top, ![]() is the mean value of
is the mean value of![]() . Since rainfall is from condensed liquid water and converged and existing airborne liquid water in lower level,
. Since rainfall is from condensed liquid water and converged and existing airborne liquid water in lower level, ![]() may be replaced by the mean value at 900 hPa and 500 hPa, we have
may be replaced by the mean value at 900 hPa and 500 hPa, we have
![]() (60)
(60)
From the analysis report provided by LGSHR1975 (1977) [42] , let the center value of ![]() equal to actual center value 12.5 mm/h, the center value of
equal to actual center value 12.5 mm/h, the center value of ![]() is 7.7 mm/h, R = 2.87 hPa×m3×kg−1×K−1, g = 9.8 m×s−2,
is 7.7 mm/h, R = 2.87 hPa×m3×kg−1×K−1, g = 9.8 m×s−2, ![]() = 7 ´ 10−3 hPa/s,
= 7 ´ 10−3 hPa/s, ![]() = 5 ´ 10−3 hPa/s and
= 5 ´ 10−3 hPa/s and ![]() at the center of rainfall intensity, with equation (59) and (60), we get
at the center of rainfall intensity, with equation (59) and (60), we get
![]() (61)
(61)
Based on 8m/s (the surface wind velocity (SWV) recorded at Suiping weather station, which is the nearest from Banqiao reservoir) and 12m/s (the SWV estimated from the physical phenomena at Banqiao reservoir), with an eye on the small scale orographic influence of Banqiao reservoir (climbing and bell-mouthed effects in the condition of NE wind), the![]() ,
, ![]() and
and ![]() at Banqiao reservoir are given by LGSHR1975 (1977) [42] (see the Table 1). From these data and
at Banqiao reservoir are given by LGSHR1975 (1977) [42] (see the Table 1). From these data and![]() , with Equation (49) and (50), we can get the
, with Equation (49) and (50), we can get the ![]() at Banqiao reservoir (see the Table 1).
at Banqiao reservoir (see the Table 1).
From Table 1, although the traditional estimated values of rainfall intensity at Banqiao reservoir, ![]() = 30.7 mm/h and
= 30.7 mm/h and ![]() = 37.0 mm/h (based on SMV = 8 m/s and 12 m/s respectively), are much less than the actual extremes of rainfall intensity 99.7 mm/h, the new estimated values
= 37.0 mm/h (based on SMV = 8 m/s and 12 m/s respectively), are much less than the actual extremes of rainfall intensity 99.7 mm/h, the new estimated values ![]() = 65.1 mm/h and 81.8 mm/h (based on SMV = 8 m/s and 12 m/s respectively), are very close to the actual extremes of rainfall intensity 99.7 mm/h.
= 65.1 mm/h and 81.8 mm/h (based on SMV = 8 m/s and 12 m/s respectively), are very close to the actual extremes of rainfall intensity 99.7 mm/h.
5. Conclusions
In this study, by introducing specific water and maximum airborne specific water into the dynamic framework on non-uniform saturated moist atmosphere, the irrational supposition, that condensed liquid water always falls immediately, is eliminated. The balance equation between water vapor and airborne liquid water is derived. From the balance equation, a new formula of precipitate rate is derived. Following the above discussion, improved dynamic equations on non-uniform saturated moist atmosphere are provided. Finally, in the supposition that ![]() is a constant (airborne coefficient
is a constant (airborne coefficient![]() ) only, using the data provided by the leading group for studying the super-heavy rain in Henan in China in August 4-8, 1975 [LGSHR1975], (1977) [42] ,
) only, using the data provided by the leading group for studying the super-heavy rain in Henan in China in August 4-8, 1975 [LGSHR1975], (1977) [42] , ![]() is estimated roughly.
is estimated roughly.
It is necessary to point out that the character of ![]() is not clear, and its accurate calculation requires a large number of data and complex work. By and large, there is still much work to estimate
is not clear, and its accurate calculation requires a large number of data and complex work. By and large, there is still much work to estimate ![]() accurately.
accurately.
Acknowledgements
This study was supported by Anhui Provincial Natural Science Foundation under Grant No. 1508085MD64, 1408085MKL60 and China Meteorology Administration Foundation under Grant No. CMAGJ2015M28.
NOTES
*Corresponding author.