Uncertainty of Wind Power Usage in Complex Terrain—A Case Study ()
1. Introduction
The public perceives using wind energy and/or other sustainable energies in pristine and/or protected areas as responsible behavior. Thus, many communities with tourist economy have strong interests in environmental protection and wind-driven power generation. In flat terrain, in the major storm tracks, the suitability of a location for this kind of power production is assessed typically based on one year of wind observations performed at 80 m to 100 m height or so, or by using long-term observations of 10 m wind speeds and calculation of the wind speeds at hub height by micrometeorological-empirical relations.
When in complex terrain, wind turbines cannot be placed atop of the highest mountains in acceptable distance to the area of demand, they have to be installed at lower elevation in the valley. Under these conditions, any assessment of the wind-energy potential becomes challenging. Unfortunately, this situation exists in many remote mountain resorts and fjord landscapes with glacier-topped mountains. In such landscapes, the frequency of major storms, the direction of the valley to the main wind direction, channeling effects, mountain-valley wind circulations and slope winds as well as radiative inversions affect wind speed [1] [2] .
The goal of our study was to investigate the uncertainty in predicting potential wind-energy production under such landscape conditions. Juneau, Alaska served as a testbed. Frequent storms moving into the Gulf of Alaska govern Juneau’s climate [3] . Being located in a fjord landscape that belongs to the Tongass National Forest, the terrain has strong impact on the wind speed. Juneau is surrounded by mountains covered by about 30 glaciers that make up the Juneau Icefield. Thus, any construction of a windfarm atop of the mountains is hardly reasonable. The frequent avalanches prohibit any icefree potential locations. The high tidal differences make any offshore location challenging from a technical point of view. Furthermore, whales and other marine mammals dislike the infra-sound created by wind turbines and stay away from these areas [4] . However, the tourists, among glacier viewing, also come to see and watch these animals. Consequently, an offshore location is prohibitive from an economic point of view. The complex terrain allows installing a windfarm at lower elevation where the fjord widens and joins other fjords.
In Juneau, cruise-ship tourism is the major economy. The port of Juneau is stop for many cruise ships on their way thru the Inside Passage and/or to the various National Parks, among others Glacier Bay National Park. In port, the cruise ships’ auxiliary engines produce energy for hoteling. This energy production makes the cruise ships the largest point sources in the area [5] .
In the fjords, when inversions exist, emissions can lead to unsightly and unexpected views for the tourists, or even haze when relative humidity is high enough [1] [6] . Thus, Juneau faces the tourism paradigm that any increase in this economy may harm why the tourists come in the first place, the pristine landscape and the possibility to see wildlife. Cruise-ship companies, the locals as well as the tourists are concerned about the cruise-ship emissions.
Princess Cruise built the first cold ironing facility in the world in Juneau. By the 2002 tourist season, five of their cruise ships used shore power when at beth in Juneau. In 2005, five of their cruise ships used the facility in total 93 times. This means that 16% of the total 586 cruise ships cold ironed [7] . Cold ironing of all cruise ships docking in Juneau would require (a) a large enough facility, (b) retrofitting cruise ships for onshore energy, and (c) ensuring the security of power supply.
At Juneau, the tides average 5 m. Therefore, a huge amount of energy stems from hydropower. Fossil fuel or natural gas powered plants exist as backup to the hydropower. The emissions per kW-hour produced by a power plant burning low-sulfur fuel is lower than that produced by any auxiliary engine running at low load. However, environmentalists argue that the emissions of a fossil fuel-burning power plant would still occur in a very clean region, just outside of Juneau. This situation brought upon the idea of investigating whether wind energy could provide the additional energy needed for cold ironing all cruise ships at beth in Juneau.
This seasonal additional energy demand makes Juneau an ideal testbed to investigate the uncertainty of the wind-energy potential in complex terrain. Since the energy is needed for cold ironing, we performed the investigation over the length of a cruise-ship season (May 15 to September 15). To achieve our goal, we used hourly output of simulated wind speeds for the tourist seasons of 2006 to 2012 [2] at hub height for eight different turbine types and applied the method described by [8] to assess potential power and capacity factors. The assessment used model-predicted wind speeds for two reasons: First, wind-speed observations rarely exist in tourism communities. Second, wind-power providers use predicted wind speeds for their three-day power-delivery forecasts.
The paper first presents the experimental design by an explanation of how the model data were generated and an introduction of the technical data used in this study as well as by a description of the model and the applied analysis methods. The result section presents an overall evaluation of the performance of the model in predicting the meteorology overall and the wind speeds in Juneau. After presenting the uncertainty in wind-power generation that results from uncertainty in wind-speed data and interannual variability in wind speeds, we address downtimes due to meteorological conditions like icing as well. All these uncertainties propagate into uncertainty of power output and capacity factors. These uncertainties are discussed followed by a discussion of consequences. The paper ends with conclusions on improving the assessment of wind-power usage in complex terrain.
2. Experimental Design
No wind observations exist for Juneau at the typical hub heights of wind turbines. Traditionally, in such situation, the potential suitability of a site for wind energy has been assessed based on an empirical power law (e.g., [9] [10] )
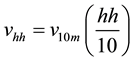 . (1)
. (1)
Here vhh and v10 are the estimated and observed mean horizontal wind speeds at hub height hh and 10 m, respectively. The exponent a varies among authors between 1/7 and 1/10. Obviously, Equation (1) does not explicitly depend on thermal stratification.
As pointed out by [8] , the vertical wind-profile function shows such a dependency. Being located in a steep valley (Figure 1), inversions frequently occur at Juneau. Furthermore, mountain-valley winds and slope winds occur under suitable large-scale conditions. Towards the end of summer, storms govern the climate of Juneau [3] . All these meteorological phenomena occur under distinct, but different thermal stratification regimes. This means Equation (1) is invalid at Juneau at least for a large part of the tourist season. Therefore, we turned to modeling to obtain wind speeds at hub height.
2.1. Model data
We used the Weather Research and Forecasting with inline chemistry [11] -[13] (WRF/Chem) model simulations performed by [2] for the seven tourist seasons of 2006 to 2012. These simulations were performed with the Advanced Research dynamic core [12] using the fully compressible nonhydrostatic prognostic equations of motions.
![]()
Figure 1. Google map of the complex terrain around Juneau, Alaska. Stars indicate the locations of (from left to the right) the assumed turbine site, whale-watching ship docks, the surface meteorological site at the Juneau International Airport, and the Juneau downtown cruise-ship docks.
The model setup used the WRF-Single-Moment 5-class cloud-microphysics scheme [14] , and a further- developed version of the Grell-Dévényi cumulus-ensemble scheme [15] to consider clouds at the resolvable and subgrid scale. The Goddard two-stream multi-band scheme [16] for shortwave radiation considers ozone and clouds. The Rapid Radiative Transfer Model accounts for multiple bands, trace gases and microphyics species for long-wave radiation [17] . Furthermore, cloud-aerosol-radiation feedbacks are considered as well [18] . The model applied the Mellor-Yamada-Janjić scheme for surface and atmospheric boundary layer (ABL) physics [19] that uses standard similarity functions according to Monin-Obukhov with Zilitinkevich thermal roughness length. The further-developed NOAH land-surface model [20] served to determine the exchange of heat and matter at the atmosphere-surface interface, and to calculate soil-temperature and soil-moisture, frozen ground and snow conditions. It also represents exchange processes over ice sheets and snow covered areas [12] .
The setup considered the following chemical packages: The Regional Acid Deposition Model version 2 chemical mechanism [21] with inline calculated photolysis rates [22] . Aerosol physics, chemistry and dynamics were dealt with by the Modal Aerosol Dynamics Model for Europe [23] , and Secondary Organic Aerosol Model [24] . Dry deposition of trace gases was considered by an Alaska adapted version of Wesely’s deposition parameterization [25] [26] . Biogenic and anthropogenic emissions were calculated depending on the atmospheric and soil conditions at the surface-atmosphere interface and hourly activity, respectively [6] [27] .
Downtown Juneau where the cruise ships dock is located lays in a narrow channel that is part of a fjord system (Figure 1). The Juneau surface meteorological site is located at the airport. Since the surrounding mountaintops are glacier-covered or protected land, we assumed a single elevation (570 m, 58.374851 N, 134.728506 W) in the wider part of the fjord close to Juneau as potential site for a wind farm [28] . Hourly wind-speed data in 80 m and 30 m height were extracted from the WRF/Chem simulations for the assumed wind-turbine site.
2.2. Technical Data
The wind-turbine types considered in this study were the Mitsubischi MWT95/2.4, Clippper Liberty, Gemesa G87-2.0, Siemens SWT 2.3-93, REpower MM92 (CCV), Vestas V-27, Northwind 100, and Entegrity EW50. The last four turbine types were included in this study because they are used widely in Alaska [28] .
No data on the turbine-power curves were available. Thus, we discretized the power curves that were published by the manufacturers. These data served to determine the empirical fitting parameters A, K, Q, B, M and u of the general logistic function
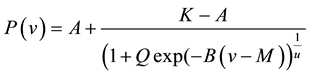 . (2)
. (2)
Here P(v) is the power generated by the respective turbine at wind speed v. Table 1 and Table 2 list the specifications of the wind turbines and the obtained empirical parameters, respectively.
Figure 2 compares the power curves of the turbines considered in this study. These curves illustrate the increase in gained power as a function of wind speed. Once the rated power of a turbine is reached, the gained power remains the same independent of any increase in wind speed. Once the cutout speed is reached, a turbine has to be shut down to avoid damage or its destruction. In the range between cut-in wind speed, and wind speed at rated power, power increases with increasing wind speed. Choosing the best turbine for a site requires identifying the turbine that would provide the highest power between cut-in wind speed and wind speed at rated for the wind speeds typically occurring at a site.
2.3. Analysis Method
We reviewed the evaluation of WRF/Chem’s performance that [2] made for June, July and August (JJA) 2006 to 2012, and that [1] made for the 2008 tourist season. These authors used data from 42 surface meteorological sites. In addition, [2] used the 0.5˚ × 0.5˚ resolution Climate Research Unit (CRU) data 3.12 [29] , and gridded data with 0.25˚ × 0.25˚ resolution of 10 m sea-surface wind speeds derived from multiple satellites [30] to assess the WRF/Chem simulations at different spatial and temporal scales. [1] also evaluated WRF/Chem’s capability to reproduce the vertical profiles of temperature, humidity, wind speed and direction by means of 246 radiosonde ascents for the 2008 tourist season.
Unfortunately, no radiosonde data were available at Juneau. At Juneau International Airport, hourly data of
![]()
Table 1. Specifications of the wind turbines considered in this study.
![]()
Table 2. Parameters used in the generalized logistic function (Equation (2)) used to model the turbines’ power curves. Values for tall turbines are from [8] .
![]()
![]()
Figure 2. Power curves of the small (left) and tall (right) wind turbines.
10 m wind-speed observations were available in bins of £ 1.5 m∙s−1, 1.5 < v £ 2.1 m∙s−1, bins of 0.5 m∙s−1 between 2.1 m∙s−1 and 5.1 m∙s−1, and 5.1 m∙s−1 < v £ 5.7 m∙s−1, and again in bins of 0.5 m∙s−1 for wind speeds > 5.7 m∙s−1. We evaluated simulated 10 m wind speeds by bias (simulated vs. observed) and root-mean square errors (RMSE) for all seven tourist seasons using these observations.
Management of spinning reserves requires highest accuracy of wind-speed forecasts in the range between cut-in wind speed and the wind speed at rated power. Thus, we evaluated predicted wind speed at different speed ranges as well.
Since long experience and expertise exists using Equation (1) for wind-energy assessment, we used the Juneau 10 m wind-speed data to determine the wind speeds at hub heights. These values are referred to as the “known standard”, hereafter. The results from Equation (1) served for comparison of the WRF/Chem predicted wind speeds at hub height with a known standard. They are by no means observations, nor a “grand truth.”We quantified the uncertainty related to the two methods in terms of mean difference
 . (3)
. (3)
and mean root-mean square difference
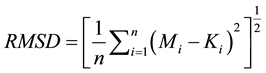 . (4)
. (4)
Here n is the number of wind-speed data, and Mi and Ki stand for the individual WRF/Chem simulated wind speeds and the wind speeds derived using Equation (1), respectively. The latter is the “known standard.” Furthermore, 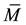 and
and 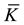 are the mean wind speeds obtained by WRF/Chem and the “known standard” when averaged over the tourist season.
are the mean wind speeds obtained by WRF/Chem and the “known standard” when averaged over the tourist season.
The wind data were examined for downtimes due to icing, wind speeds below the cut-in wind speed and above the speed of rated power and the cutout wind speed. The percentage of time in a tourist season that a turbine could theoretically generate power was determined for each turbine as well.
The wind potential was assessed using the method outlined by [8] . Two-parameter Weibull distributions were fitted to the cumulative historgrams of each tourist season. The average power output was calculated by
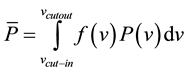 . (5)
. (5)
Here f(v) is the probability-density function of a given wind speed, v (Figure 2), and vcut-in, and vcutout are the cut-in and cutout wind speeds listed in Table 2. The capacity factor
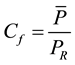 (6)
(6)
is the ratio of the average power output 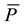 and the rated power, PR of the respective wind turbine (Table 1).
and the rated power, PR of the respective wind turbine (Table 1).
Comparison of the wind-power potentials obtained for the seven tourist seasons served to investigate the interannual variability, i.e. uncertainty in the long-term reliability of wind speed and potential wind-power production.
3. Results
3.1. Evaluation
[2] evaluated the WRF/Chem results by observations from 42 surface meteorological sites with hourly data, the monthly means of 2 m temperature, diurnal temperature range and relative humidity of Climate Research Unit data, and 10 m sea-wind data for June, July and August (JJA). At the 42 sites, WRF/Chem showed biases (simulated minus observed) of −1.6˚C, 7% (absolute), and 1.72 m・s−1of −1.6˚C, 7% (absolute), and 1.72 m・s−1 for 2 m temperature, 2 m relative humidity, and 10 m wind speed, respectively; RMSEs were 1.3˚C, 6%, and 1.99 m・s−1. According to the CRU data, JJA biases of 2 m temperature, diurnal temperature range, and relative humidity over land were −0.7˚C, −5.3˚C, 15%, and RMSEs were 2.3˚C, 4.3˚C, and 19%, respectively. Note that the CRU data only exist over land, and have no wind data. Over the ocean, the gridded 10 m sea-wind speed data suggested an overall bias and RMSE of −1.1 m・s−1 and 0.4 m・s−1, respectively.
Simulated and observed temperature profiles correlated well at on average r = 0.85 with a negligible overall warm bias of 0.1˚C, and low RMSE of 1.8˚C [1] .WRF/Chem overestimated the overall dew-point temperature profile between 0.2˚C and to up to 3.6˚C in areas of strong wind shear (>40˚). WRF/Chem simulated and observed wind-speed profiles correlated with r = 0.69. WRF/Chem captured the upper air wind-speed profiles accurately, but had some difficulties below 2500 m when the magnitude of shear, and wind-speed variability were high over a relatively thin atmospheric layer [1] . Simulated and observed regions of wind shear matched well. WRF/Chem overestimated wind speeds by 0.2 m∙s−1 to 1.2 m∙s−1 from the surface to about 1100 m. On average, wind-speed biases remained less than 0.7 m∙s−1 in the surface layer and lower ABL. Furthermore, WRF/Chem reproduced the wind-speed variance well (5.80 m2∙s−2 vs. 5.67 m2∙s−2) [1] .
3.1.1. 10 m Wind Speed at Juneau
At the Juneau surface meteorological site, mean 10 m wind speeds during tourist seasons ranged from 2.3 m∙s−1 in 2007 to 2.9 m∙s−1 in 2006, and 2011 (Table 3). The WRF/Chem-derived mean wind speeds at 10 m height ranged from 3.9 m∙s−1 in 2007 and 2008 to 4.5 m∙s−1 in 2011. Over all tourist seasons, the overall mean 10 m wind speeds were 4.3 m∙s−1 and 2.6 m∙s−1 for WRF/Chem and observations, respectively. Note that all meteorological models tend to overestimate 10 m wind speeds under stagnant situations [31] like inversions that frequently occur in Juneau.
We evaluated wind speed at 10 m height at Juneau International Airport for the tourist seasons (Table 3) using all data recorded, i.e. also those data that suggested no wind. According to the evaluation, WRF/Chem overestimated 10 m wind speed by 1.4 m・s−1 (2008) to nearly 2 m・s−1 (2009), and 1.6 m∙s−1 on average. Analysis of the observed 10 m wind-speed data showed no recorded 10 m wind speeds greater than zero, but lower than 1.5 m∙s−1 due to the start-up speed of the anemometer. Zero wind speed due to start-up speed existed 25% to 32% of the time during a tourist season, and 28% of the time on average. Consequently, WRF/Chem-obtained 10 m wind speeds below 1.5 m∙s−1 partly contributed to the “overestimation” of wind speed at 10 m height. Excluding all observed events with zero wind speed form the calculation provided biases between 0.5 m∙s−1 and 1.3 m∙s−1 and 0.9 m∙s−1 on average over all tourist seasons. This finding and comparison with the percent of conditions below start-up speed showed that WRF/Chem still overestimated 10 m wind speed. The systematic instrument errors affected the calculated means and standard deviations of observed 10 m wind speed, as well as bias, and RMSEs listed in Table 3. In the following, all discussion considers all recorded 10 m wind-speed data.
On average over all tourist seasons, the standard deviations of simulated and observed 10 m wind speed were 2.9 m∙s−1 and 2.2 m∙s−1, respectively. Since the difference exceeds the typical increments of 0.4 m∙s−1 to 0.5 m∙s−1 of the 10 m wind-speed records, this finding is likely not an artifact of the data. Instead, it suggests higher temporal 10 m wind-speed variability in the model than observed. Of course, some of the differences between the standard deviations calculated from the simulations and observations resulted from instrumental shortcomings
![]()
Table 3. Mean and standard deviation (StDev), bias of 10 m, 30 m, and 80 m wind speeds at Juneau for May 15 to September 15 of all seven years in m∙s−1. The numbers in brackets refer to the observations at 10 m height, and the “known standard” at 30 m and 80 m as estimated by Equation (1). MD, RMSE and RMSD are the mean difference, root-mean square error and root-mean square difference, respectively. Note that the values related to 10 m height are performance-skill scores, while those at 30 m and 80 m are for comparison of the WRF/Chem predicted values to “known standard”.
and/or artifacts, i.e. the start-up speed and over speeding of the anemometer when wind calms down. The standard deviations of simulated 10 m wind speeds indicated differences in intra-annual variability of 10 m wind speed in the order of up to 0.6 m∙s−1.
Seasonal RMSEs ranged from nearly 3.0 m∙s−1 (2008) to 3.8 m・s−1 (2009, 2011) with 3.5 m∙s−1 on average (Table 3). Some of the bias and RMSE related to mistiming of frontal passages. Such errors are of minor relevance for the feasibility of wind-energy generation in general. The wind would have been available, but with temporal offset. However, the offset may become important, when penalties for non-delivery are to be paid. An offset of a couple of hours can mean an incorrect daily estimate when the offset occurs around midnight.
Some of the wind-speed errors were due to local effects. The surface meteorological site at the airport is in a deep fjord (Figure 1) that is not well resolved by the model. Our evaluations showed that WRF/Chem captured the variability in 10 m wind speed at the Juneau meteorological site acceptably most of the time.
The assumed turbine site is about 10 km bird route away from the location of the surface meteorological site (Figure 1). The turbine site is close to the water at a location where the fjord is wide. Steep mountains exist about 2 km to its north, while it has about 4.5, 7.5, 2.5, 8, and 2 km of open water to the west, southwest, south, southeast and east, respectively. The fjord’s orientation is a couple of degrees off from that at the airport. At the airport, the main wind directions are north or easterly winds [3] . Since wind experiences less friction over water than in steep tree-covered or urban land, i.e. the land cover close to the meteorological site, we can assume that the slight overestimation of 10 m wind speed is of minor concern for the assessment of wind-power potential at the turbine site.
The standard deviation of the annual means can be interpreted as intraseasonal variability [32] . The standard deviation calculated for the seven tourist seasons (overall) can be interpreted as interannual variability. Thus, it can serve to assess uncertainty that would result from choosing a certain tourist season for a wind-potential study. The standard deviations for the observations are of about the same magnitude as the tourist-season means, which suggests strong dependence of the assessment on the choice of tourist season. In the case of the WRF/ Chem-simulated wind speeds, the standard deviation is notably smaller than the mean. This finding suggested lower uncertainty with respect to the choice of season than for the “known standard”. This result is partly because WRF/Chem also predicted wind speeds below the spin-up velocity and overestimated wind-speed.
For wind-power estimates, the biases around cut-in and wind speed at rated power are critical. On average over all tourist seasons, wind-speed biases first decreased with increasing wind speed and then increased with increasing wind speed (Figure 3). This means that on average, WRF/Chem overestimated low and underesti- mated high 10 m wind speeds. Around zero-bias occurred for 10 m wind speeds between 4.1 m∙s−1 and 4.6 m∙s−1. Lowest bias occurred in different wind-speed bins in different years. At wind speeds exceeding 8.3 m∙s−1, too few observed events (<30) existed in individual tourist seasons and/or bins for reliable statistics. However, enough data existed for reliable statistics over all tourist seasons. Its results suggested that for 10 m wind speed greater than 8.3 m∙s−1 biases remained less than 2 m∙s−1 on average.
The RMSEs differed up to about 1.8 m∙s−1 among tourist seasons for simulated 10 m wind speeds less than
![]()
![]()
Figure 3. Mean bias (left) and RMSE (right) as a function of observed 10 m wind speeds for the various tourist seasons and on average over all seven tourist seasons. Note that for 10 m wind speeds exceeding 8.3 m∙s−1 not enough events occurred in individual bins for a solid statistic in individual seasons, but enough data existed for calculation of an overall error. Lines for individual seasons are continued for errors greater than 8.3 m∙s−1 only to illustrate the spread. See text for details. Bins are named after the lowest value belonging to the bin.
2.6 m∙s−1 (Figure 3). On average over all tourist seasons, wind-speed RMSEs were highest below 2.6 m∙s−1. Except for 2009, RMSE showed a minimum for wind speeds between 2.6 m∙s−1 and 6.1 m∙s−1 or so. The RMSE determined over all tourist seasons (yellow line in Figure 3) suggested that accuracy decreased slightly with increasing wind speeds after passing a plateau of similar errors for 10 m wind speeds between about 2.6 m∙s−1 and 5.1 m∙s−1. In this range, 10 m wind-speed RMSEs varied around 2.6 m∙s−1 on average.
3.1.2. Uncertainty of Wind Data
The Weibull distributions of observed 10 m wind speed indicated up to 8% interannual variability for wind speeds that were around the maximum probability of about 3 m∙s−1 (Figure 4). Consequently, interannual varia-
bility in wind speeds derived for 30 m and 80 m by Equation (1) was highest for the most probable wind density too. The peak of probability density flattened and shifted towards increased wind speed with height. At the same time, maximum probability occurred between slightly over 3 m∙s−1 in 2009 to 4.5 m∙s−1 in 2006. This means interannual variability increased with height as well.
The WRF/Chem used the prognostic equations of motion to predict wind speed. WRF/Chem 10 m wind speeds showed a comparatively higher interannual variability at highest probability density than the observations (Figure 4). A major reason was that WRF/Chem can predict wind speeds below the spin-up velocity of the anemometer. For the simulations, maximum probability was less than determined from the observations and it occurred at wind speeds below 3 m∙s−1.
Interannual variability of observed 10 m wind speeds was higher with increasing wind speed than in the simulations. The non-linear behavior of over-speeding of the anemometer as wind speed decreased may be part of the reason for the differences. The tendency of WRF/Chem to overestimate 10 m wind speeds extended the tail of probability density towards increased wind speeds. These findings suggest that the results of the empirical Equation (1) bear different uncertainty at both low and high wind speeds.
Simulated wind speeds at 30 m and 80 m height showed highest probability for all years for wind speeds less than 3 m∙s−1. Like for the probability densities derived from the observations by Equation (1), maximum probability density decreased with increasing height. Due to the nature of Equation (1), the individual tourist seasons kept their ranking with respect to the magnitude of maximum probability densities among each other at all heights (Figure 4).
WRF/Chem, however, considered the vertical profile function of the horizontal wind speeds, as the prognostic equations of motion were solved. These facts allowed for a variety of wind changes with height. Consequently, highest probability density varied not only in magnitude among tourist seasons, but also in their relation at 30 m and 80 m.
Table 3 illustrates that the WRF/Chem-simulated and Equation (1) estimated wind-speed mean differences reached up to 2.1 m∙s−1 at both heights. Root-mean-square differences amounted up to 4.4 m∙s−1 and 4.9 m∙s−1 at 30 m and 80 m height, respectively, and occurred in different tourist seasons (2012 vs. 2009).
Since in the literature, the exponent a used in Equation (1) varies among authors between 1/7 and 1/10 (e.g., [9] [10] ), a sensitivity study was performed with the other extreme as well. However, the choice of the exponent did not change the general findings [28] .
We used the WRF/Chem-predicted wind speeds and solved Equation (1) for the exponent. Figure 5 illustrates that the exponent varied over the tourist season. Even when smoothing with a Fast-Fourier Approximation the exponent remained far from being a constant. This means that high uncertainty will exist when using this empirical equation instead of observations or predictions at hub height for any wind-power assessment.
![]()
![]()
Figure 5. Temporal variation of the exponent in Equation (1) according to the WRF/Chem simulations as obtained for the 2006 tourist season at 30 m (left) and 80 m (right) height. Note that results for other tourist seasons look similar (therefore not shown).
3.2. Uncertainty Due to Meteorology Induced Downtimes
The WRF/Chem data suggested that during the examined tourist seasons no loss due to icing would have occurred. At Juneau, the minimum temperatures at hub heights were 2.1˚C, 2.4˚C, 2.7˚C, 1.3˚C, 1.7˚C, 2.3˚C, and 3.5˚C for 2006, 2007, 2008, 2009, 2011, and 2012, respectively.
Simulated wind speeds at hub height never exceeded the cutout wind speeds of any turbine except in 2009 and 2011. Then, however, wind speeds exceeded the cutout wind speed less than 1% of the tourist season, i.e. about 3 to 4 h at most. The assessment using wind-speed data estimated by Equation (1) suggested that no downtimes would occur due to wind speeds exceeding the cutout speeds. It also suggested no exceedance of the wind speed at rated power most of the time. The percentage of hours above the wind speed at rated power as obtained with the WRF/Chem-predicted data varied among tourist seasons. It was largest for the Mitsubishi and the Entegrity for the tall and small turbines, respectively (Table 4).
The percentage of simulated wind speeds above the cut-in wind speed varied less than 11% (absolute) among the 7 tourist seasons and up to 16% (absolute) among turbine types (Table 5). At the chosen site, the Mitsubishi and REpower would have been able to harvest wind energy about 65% of the time on average followed by the Northwind 100 with 58%.
As expected, the probability for higher wind speeds was slightly higher at 80 m than 30 m (Figure 3). The probability density varied the strongest among years for simulated wind speeds less than 6 m∙s−1 and 3 m∙s−1 at 30 m and 80 m height, respectively. This means that the percentage of wind energy generated just above cut-in wind speed varied the strongest among years and stronger for the small than tall turbines. Interannual differences
![]()
Table 4. Percentage of hours with WRF/Chem predicted wind speeds at hub height being above the wind speed at rated power (Table 1) at the Juneau site for the wind turbines considered in this study for the tourist seasons of 2006 to 2012. Values in brackets list percentage of usable wind speeds derived with Equation (1) based on observed 10 m wind speeds for comparison to the “known standard.” The column named “overall” gives the mean over all seven tourist seasons.
![]()
Table 5. Percentage of hours with WRF/Chem-predicted wind speeds at hub height being above cut-in and below cutout wind speed (Table 1) at the Juneau site for the wind turbines considered in this study over the tourist seasons of 2006 to 2012. Values in brackets list percentage of wind speeds derived with Equation (1) based on observed 10 m wind speed for comparison to “known standard.” “Overall” denotes to the average over all seven tourist seasons.
in probability density of wind speeds around or above rated power are comparably small, i.e. about 50% or less than that around cut-in speed.
At hub height of tall turbines, WRF/Chem-simulated wind speeds suggested up to 12% (10% over all tourist seasons) more hours with suitable wind speeds than the “known standard” suggested (Table 5). For small turbines, WRF/Chem-predicted percentage of hours above cut-in speed exceeded those obtained by the “known standard” between 1% and 20%. Comparison with the first and second moments of the statistics led to the conclusion that uncertainty in percent hours above cut-in speed increased with increasing interannual and intraseasonal variability.
Table 5 reveals that major uncertainty resulted from different cut-in speeds. The percentage of overall hours with predicted wind speeds between cut-in and cutout speed had a standard deviation of 1% (~30 h) for the Clipper Liberty, Gamesa G87, and Siemens SWT, of 3% (~89 h) for the Mitsubishi, REpower, and Northwind 100, and 4% (~119 h) for the Entegrity. The “known standard” indicated a slightly higher uncertainty related to the assessed tourist season than using WRF/Chem. For all turbines, the standard deviation was 5% (~149 h) except for the Entegrity with 6% (179 h).
The Mitsubishi, REpower, Gamesa G87 and Entegrity had the highest percentage of hours with wind speeds above the wind speed at rated power. The interannual uncertainty in hours above the rated power was about 1% for all turbine types examined here. However, the uncertainty related to the tourist season chosen for assessment was less when using the “known standard” than when using WRF/Chem-predicted wind speeds.
3.3. Uncertainty in Power Output
The average power output shows the potential of the site itself for a given wind-turbine type. The average power output varies among turbines due to their different technical data (Table 1). Over the seven tourist seasons, the ranking in average power output among the turbines remained the same (Figure 6). Out of the tall turbines, the Mitsubishi MWT95/2.4 provided the highest average power output closely followed by the Clipper Liberty and Siemens SWT-2.3-93. The Vestas V-27 produced the highest average power output of the small turbines.
For all tall turbines, their average power output was lowest and highest in the 2007 and 2006 tourist season, respectively. The differences in average power output among the seven tourist seasons exceeded that found among turbine types for the tall turbines (Figure 6). In the 2007 tourist season, the Mitsubishi, for instance, had an average power output of 150 kW less than in the 2006 tourist season.
For the small turbines, the lowest average power output occurred in the 2007 tourist season too. However, the 2012 tourist season saw the highest average power output. The difference in average power between the 2012 and 2007 tourist season for the Vestas V-27, for instance, amounted about 10 kW, i.e. similar to the average power production of an Entegrity EW50 (Figure 6). These findings suggest that the potential of the assumed site differs with height and is very sensitive to interannual variability in wind speed.
Compared with the “known standard”, at both 30 m and 80 m height, average power output was about twice as high when the assessment based on WRF/Chem-predicted wind speeds (Figure 5). The same applied for interannual variability. According to the assessment with predicted wind speeds, the Mitsubishi would have produced the highest average power output of the tall turbines in all seven years. This means the choice for the turbine would be independent of the year used for the assessment. However, when in the assessment with Equation (1) derived wind speeds, a tourist season with low 10 m mean wind speed were used by accident, the REpower would have provided the highest average power output. This means in an assessment using Equation (1), to generate the wind-speed data at hub height, the decision for a wind-turbine type would depend on the tourist season used in the assessment.
3.4. Capacity Factor
The capacity factor describes the maximal ability of a wind turbine at a site. Table 1 displays the average capacity factors over all tourist seasons. The capacity factors varied stronger among tourist seasons than among wind-turbine types (Figure 7). Out of the small turbines, the Northwind 100 had the highest capacity factor no matter whether wind speeds were calculated by Equation (1), or whether they were predicted by WRF/Chem. The Northwind 100’s lowest capacity factor occurred in 2007, but it still exceeded the capacity factors reached by the other small turbines in most seasons.
Independent of the wind-speed data source, the REpower MM92 always showed the highest capacity reaching up to 26.8% in the 2006 tourist season when using the WRF/Chem data (Figure 7). The REpower MM92 also had the highest average capacity factor closely followed by the Gamesa Ga7-2.0, Mitsubishi MWT95/2.4, and Siemens SWT-2.3-93 (Table 1). The average capacity factor of the Clipper Liberty was notably lower than that of the others. The capacity factors of the tall wind turbines were similar among each other, but varied, on average, between 18% and 24.7% for the different tourist seasons. The capacity factors of the REpower MM92 exceeded the mean notably, while those of the Clipper Liberty remained notably below average (Figure 7).
The assessment using Equation (1) for gaining the wind speeds at hub height suggested that the site were unsuitable according to the capacity factors (Figure 7). This assessment was independent of the tourist season for which the study was performed. On the contrary, the study with predicted wind speeds indicated that the site has acceptable capacity for the REpower MM92 even though on the low end. If the 2007 tourist season were chosen for the assessment, a decision might have depended on the threshold that the wind-power providers set for themselves for rentability/margin of profit.
3.5. Discussion
The mean differences between the wind speeds predicted by WRF/Chem and estimated by Equation (1) (“known standard”) for 30 m height were of similar magnitude than the mean bias between simulated and observed wind speeds at 10 m height (Table 3). The same was true for wind speeds at 80 m. The RMSD between simulated and Equation (1) derived wind speeds at 30 m were 13% to 26% higher than the RMSE of 10 m wind speed in the various tourist seasons and 14% on average. In the case of 80 m, these RMSDs were 23% to 40% higher than the RMSE of wind speed at 10 m height in the various tourist seasons, and 29% on average.
As aforementioned, the anemomenter’s pickup velocity is 1.5 m∙s−1. When using Equation (1), this value corresponds to 1.75 m∙s−1 and 2.01 m∙s−1 at 30 m and 80 m, respectively. These values are below cut-in speed for all turbines. As discussed in Section 3.1.1., WRF/Chem performed best in predicting wind speeds at 10 m height for speeds between 4.1 m∙s−1 and 4.6 m∙s−1, and between 2.6 m∙s−1 and 5.1 m∙s−1 with respect to bias and RMSE, respectively. Due to the lack of data, we used Equation (1) to assess the range of uncertainty at 30 m and 80 m height. The “known standard” and WRF/Chem agreed best for wind speeds between 3.0 m∙s−1 and 6.0 m∙s−1 (5.5 m∙s−1 and 6.9 m∙s−1) at 30 m (80 m) height. This range included the cut-in speed for the small turbines, but exceeded cut-in speed for the tall turbines. Accuracy was comparatively lower at 10 m wind speeds in excess of these values. However, wind-power prediction requires highest accuracy between cut-in speed and the speed of rated power as well as around cutout speed. The former strongly affects the forecast of producible power. The latter serves for safety and avoidance of turbine destruction.
4. Conclusions
Many communities, whose major economy relies on tourism, look to wind energy as a clean energy source to provide parts of the (additional) energy demand of the tourist season. These communities face the tourism paradigm that an increase in seasonal tourism means a seasonal increase in energy demand, but its production with fossil resources affects the pristine landscape (glaciers, visibility) that attracts the tourists. Since tourism communities are often located in complex terrain, this study examined the uncertainty in wind-energy assessments using Juneau, Alaska as a testbed. Juneau is located in a fjord landscape with steep valleys and glacier-covered mountains.
The assessment used model-predicted wind speeds for two reasons. First, wind-speed observations on tall masts and/or by wind profilers may cause political difficulties in such communities and therefore, rarely exist. Second, once a wind turbine/farm is in place, power forecasts base on predicted wind speeds. Thus, the method applied in this study permits not only conclusions with respect to the suitability of a site, but also with respect to the uncertainty in wind-power delivery estimates during the production phase.
Predicted wind speeds at hub height for three small and five tall turbines and 10 m wind speeds were extracted from evaluated WRF/Chem simulations [1] [2] that were performed for seven tourist seasons (May 15 to September 15). The uncertainty was also assessed by use of 30 m and 80 m wind-speed data estimated by an empirical equation (Equation 1) from observations at 10 m height.
The evaluation of predicted 10 m wind speed revealed that uncertainty differed among wind-speed bins. Uncertainty was highest for wind speeds less than 2.6 m∙s−1. The lowest bias (RMSE) occurred for wind speeds between 4.1 (2.6) m∙s−1 and 4.6 (5.1) m∙s−1, i.e. around and slightly above cut-in wind speed. Any assessment for a turbine site as well as later any wind-power forecast, however, would require lowest uncertainty between cut- in speed and the speed at rated power as well as around cutout speed. This means that current modeling capabilities have to be improved to extend the range of best performance in predicting wind speed to these wind-power relevant ranges.
We applied the method by [8] to calculate the power and capacity factors for the seven tourist seasons and eight turbine types. Our study revealed that interannual variability in wind speed at hub height can cause differences in produced power that are of the order of the differences among turbine types with similar hub height. This finding leads to the conclusion that assessment of a site may depend on the meteorological conditions of the year chosen in the assessment. When using a semi-empirical equation to estimate wind-speed at hub heights from observations at 10 m height, the choice of the assessment year could even lead to a different choice of wind turbine. However, when using predicted wind speeds, interannual variability in wind speed did not affect the ranking of the individual turbine types when comparing them with respect to power production and capacity factor. Thus, one may conclude that predicted wind speeds reduce uncertainty as compared to application of a semi-empirical equation. Another main advantage of using data from a well evaluated model is that one can assess concurrently the potential down-times due to icing. Numerical Weather Prediction models namely can also provide temperatures at hub height. Knowing the potential percentage of icing risk reduces the uncertainty in the assessment of wind-power production.
The analysis showed that uncertainty in assessed capacity amounted up to about 8% (6%) among the seven seasons and 8% (5%) among turbine types when using WRF/Chem-predicted wind speeds at 80 m (30 m) height. However, the ranking among turbines with respect to capacity factors was independent of the tourist season used in the assessment.
Despite both methods for obtaining wind speeds at 30 m and 80 m height showed highest capacity for the same small and tall turbine, respectively, the assessment might have been dependent on the method applied. Large differences (up to 40%) occurred between capacity and power derived when using wind data derived from Equation (1) and WRF/Chem-predicted wind speeds. This finding suggests that for assessment of wind-farm- sites wind-profiler measurements are an urgent need and cannot be substituted by application of Equation (1). One also has to conclude that future work should aim at reducing the uncertainty in wind-speed prediction between cut-in speed and speed at rated power as well as around cutout speed. Predicted wind speeds namely serve wind-energy providers to assess their production over the next days. Therefore, wind-speed measurements made at hub height of existing wind farms should be used to evaluate and improve (if needed) the model that the wind-energy provider will use for their near-term assessment of generated wind power. Doing so can minimize penalties for incorrect power-delivery estimates.
Acknowledgements
The authors thank M.A. Pirhalla, G. Sellhorst, J.M. Madden, J. Smith, J. Bange, and the anonymous reviewers for fruitful discussion and helpful comments, and the Research Computing Support of the Geophysical Institute at the University of Alaska Fairbanks for HPC and CPU time. Khordakova was funded through a German scholarship. The simulations were made within the framework of the National Parks Service contract P11AT30883/ P11AC90465. Hourly surface meteorological data came from the National Climatic Data Center, National Data Buoy Center, and the Alaska Department of Transportation.