Doubly Periodic Riemann Boundary Value Problem of Non-Normal Type for Analytic Functions on Two Parallel Curves

Lixia Cao^*, Huijun Zheng

School of Mathematics and Statistics, Northeast Petroleum University, Daqing, China.

DOI: 10.4236/apm.2015.51006                

Abstract

In this paper, we present and study a kind of Riemann boundary value problem of non-normal type for analytic functions on two parallel curves. Making use of the method of complex functions, we give the method for solving this kind of doubly periodic Riemann boundary value problem of non-normal type and obtain the explicit expressions of solutions and the solvable conditions for it.

Keywords

Doubly Periodic, Holder Continuous Functions, Riemann Boundary Problem, Non-Normal Type

1. Introduction

Classical Riemann boundary value problems (RBVPs), doubly periodic or quasi-periodic RBVPs and Dirichlet Problems for analytic functions or for polyanalytic functions, on closed curves or on open arcs, have been widely investigated in papers [1] -[8] . The main approach is to use the decomposition of polyanalytic functions and their generalization to transform the given boundary value problems to their corresponding boundary value problems for analytic functions, and the fundamental and important tool for which is the Plemelj formula. Professor L. Xing proposed the Periodic Riemann Boundary Value Inverse Problems in paper [9] , and then various inverse RBVPs for generalized analytic functions or bianalytic functions have been investigated in papers [10] - [13] .

In present paper, we present a kind of doubly periodic RBVP of non-normal type for analytic functions on two parallel curves. On the basis of the results for normal type in paper [14] , we give the method for solving this kind of doubly periodic RBVP of non-normal type and obtain the explicit expressions of solutions and the solvable conditions for it.

2. Doubly Periodic RBVP of Non-Normal Type on Two Parallel Curves

Suppose that, 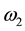are complex constants with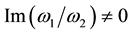, and P denotes the fundamental period parallelogram with vertices. The function

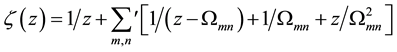
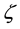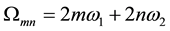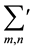is called the Weierstrass -function, where, and denotes the sum for all

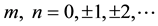, except for.

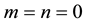Let 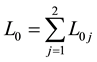be the set of two parallel curves, lying entirely in the fundamental period parallelogram P,

not passing the origin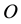, with endpoints being periodic congruent and having the same tangent lines at the periodic congruent points. Let D₁, D₂, D₃ denote the domains entirely in the fundamental period parallelogram P, cut by L₀₁ and L₀₂, respectively. Without loss of generality, we suppose that 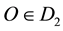see Figure 1. Let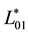, be the curves periodically extended for L₀₁ and L₀₂ with period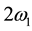, respectively. And be the curves periodically extended for with.

We aim to is to find sectionally holomorphic, doubly periodic functions and, satisfying the following boundary conditions

(1)

where, with, and, are doubly periodic with,. are the boundary values of the function, which is analytic in and, belonging to

the class on L_0j, satisfying the boundary conditions (1), and are the boundary values of the func-

tion, which is analytic in, belonging to the class on, satisfying the boundary conditions (1). While

,

where is doubly periodic, where

Figure 1. parallel curves in the fundamental period parallelogram P.

With k, t and being integers. Without loss of generality, we suppose that with c_s,

, as well as and

.

Since plays the same roles as other points on, it is natural to require that the unknown functions are bounded at, that is, the unknown functions and are both bounded on and. And if we allow the solution has poles of order at, it is actually to solve problem (1) in DR_m.

3. Preliminary Notes

with. Now we call the integer the index of problem (1), where is the integer satisfying

.

Since can only be 0 and, the index can only take.

Set

(2)

(3)

We can easily see that will have singularities at most less than one order near the endpoints and . Let

(4)

then we have

, ,

where and. Thus is not doubly periodic generally. In fact, is doubly periodic if and only if

, is positive integer for. (5)

Lemma 1. Formula (5) is valid if and only if

,.

And if both and are true, then we have and, where, are all integers.

4. Solution for Problem (1)

Problem (1) can be transferred as

(6)

Case 1. If formula (5) holds, that is, is doubly periodic, then by Lemma 1 we have

. (7)

The function always has singularities less than one order near the endpoints and whatever. And then both

and

must belong to class H or class H^* on L₀₁ and L₀₂, respectively.

Set

(8)

, (9)

then (6) can be rewritten as

(10)

where and (or and) denote the boundary values of the functions and. By the definitions of and, we see that

(i) has no zeros in domain;

(ii) The part of which has zeros in domain is;

(iii) The part of which has zeros in domain is;

(iv) has no zeros in domain.

Write

When we solve problem (1) in, the unknown function is -order at. And now we will meet three kinds of situations in solving problem (1) in, according to the value of.

When, problem (1) is solvable without any restrictive conditions and the general solution is given by

(11)

where are arbitrary constants.

When, problem (1) is solvable if and only if the restrictive conditions

(12)

are satisfied, and now the solution is given by

(13)

where is arbitrary constant.

When, is the zero point of order of the function, and due to this the solution for problem (1) has order at the point. Now the solution for problem (1) can still be given by (13), but the following two restrictive conditions are necessary:

, (14)

(15)

(when, the condition (15) is unnecessary).

Case 2. If formula (5) fails to hold, then by Lemma 1 we see that. Let

,

then the function become doubly periodic, and function has singularities at most

less than one order near the endpoints and. Thus now, we can transform (6) to

(16)

When, the two functions, belong to class

or class on and, respectively. Write

(17)

. (18)

By (17) and (18), we can rewrite (16) as

(19)

Now we will meet two kinds of situations in solving problem (1) in.

(a) When, the function is an entire function. And we can write it without counting nonzero constant as

,

where are determined by the identity.

When, problem (1) is solvable without any restrictive conditions and the general solution is given by

(20)

where are arbitrary constants.

When, problem (1) is solvable if and only if the restrictive conditions

(21)

are satisfied, and the general solution is given by

(22)

where is arbitrary constant.

3˚ When, problem (1) is solvable if and only if the restrictive conditions

(23)

are satisfied, and the general solution can still be given by (22) but with

(24)

(b) When fails to hold, the function has singularity of one order at z = 0,

and has singularities at most less than one order near the endpoints and, has a zero of order one at.

When, problem (1) is solvable and the general solution is given by

(25)

with the restrictive condition that

,

which is to ensure that the solution be finite at, where are arbitrary constants.

When, problem (2.1) is solvable if and only if the restrictive conditions

(26)

are satisfied, and now the solution is given by

(27)

which is finite at owing to its structure.

When, if and only if both conditions (26) and the following conditions

(28)

(29)

(when, (29) is unnecessary) are satisfied, problem (1) is solvable and the solution is given by

(30)

Funding

The project of this thesis is supported by “Heilongjiang Province Education Department Natural Science Research Item”, China (12541089).

Conflicts of Interest

The authors declare no conflicts of interest.

References

[1]	Balk, M.B. (1991) Polyanalytic Functions. Akademie Verlag, Berlin.
[2]	Begehr, H. and Kumar, A. (2005) Boundary Value Problems for the Inhomogeneous Polyanalytic Equation I. Analysis: International Mathematical Journal of Analysis and its Application, 25, 55-71.
[3]	Du, J.Y. and Wang, Y.F. (2003) On Boundary Value Problems of Polyanalytic Functions on the Real Axis. Complex Variables, 48, 527-542. http://dx.doi.org/10.1080/0278107031000103412
[4]	Fatulaev, B.F. (2001) The Main Haseman Type Boundary Value Problem for Metaanalytic Function in the Case of Circular Domains. Mathematical Modelling and Analysis, 6, 68-76.
[5]	Lu, J.K. (1993) Boundary Value Problems for Analytic Functions. World Scientific, Singapore.
[6]	Mshimba, A.S. (2002) A Mixed Boundary Value Problem for Polyanalytic Function of Order n in the Sobolev Space Wn, p(D). Complex Variables, 47, 278-1077.
[7]	Muskhelishvili, N.I. (1993) Singular Integral Equations. World Scientific, Singapore.
[8]	Wanf, Y.F. and Du, J.Y. (2006) Hilbert Boundary Value Problems of Polyanalytic Functions on the Unit Circumference. Complex Variables and Elliptic Equations, 51, 923-943. http://dx.doi.org/10.1080/17476930600667692
[9]	Xing, L. (1995) A Class of Periodic Riemann Boundary Value Inverse Problems. Proceedings of the Second Asian Mathematical Conference, Nakhon Ratchasima, October 1995, 397-400.
[10]	Wang, M.H. (2006) Inverse Riemann Boundary Value Problems for Generalized Analytic Functions. Journal of Ningxia University of Natural Resources and Life Sciences Education, 27, 18-24.
[11]	Wen, X.Q. and Li, M.Z. (2004) A Class of Inverse Riemann Boundary Value Problems for Generalized Holomorphic Functions. Journal of Mathematical, 24, 457-464.
[12]	Cao, L.X., Li, P.-R. and Sun, P. (2012) The Hilbert Boundary Value Problem With Parametric Unknown Function on Upper Half-Plane. Mathematics in Practice and Theory, 42, 189-194.
[13]	Cao, L.X. (2013) Riemann Boundary Value Problem of Non-Normal Type on the Infinite Straight Line. Applied Mathematics, 4, 1126-1230.
[14]	Cao, L.X., Li, X.W. and Lin, C.X. (2014) A Kind of Doubly Periodic Riemann Boundary Value Problem on Two Parallel Curves. Advances in Pure Mathematics, 4, 627-634.