1. Introduction
Poisson process is used to model the occurrences of events and the time points at which the events occur in a given time interval, such as the occurrence of natural disasters and the arrival times of customers at a service center. It is named after the French mathematician Siméon Poisson (1781-1840). In this paper, we first give the definition of the Poisson process (Section 2). Then we stated some theroems related to the Poisson process (Section 3). Finally, we give some examples and compute the relevant quantities associated with the process (Section 4).
2. What Is Poisson Process?
A Poisson process with parameter (rate) 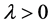 is a family of random variables
is a family of random variables 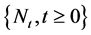 satisfying the following properties:
satisfying the following properties:
1)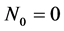 .
.
2) 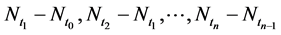 are independent random variables where
are independent random variables where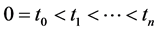 .
.
3) 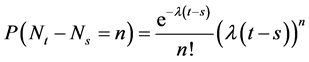 for
for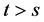 .
.
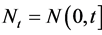 can be thought of the number of arrivals up to time t or the number of occurrences up to time t.
can be thought of the number of arrivals up to time t or the number of occurrences up to time t.
3. Some Facts about the Poisson Process
We give some properties associated with the Poisson process. The proofs can be found in [1] or [2] . If we let 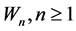 be the time of the
be the time of the 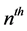 arrival
arrival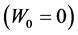 , and we let
, and we let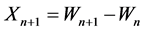 ,
, 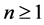 , be the interarrival time
, be the interarrival time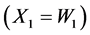 . Then we have the following theorems:
. Then we have the following theorems:
Theorem 1 The 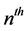 arrival time has the
arrival time has the 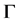 -distribution with density function
-distribution with density function![]() , for
, for ![]()
Theorem 2 The interarrival times ![]() are independently exponentially distributed random variables with parameter
are independently exponentially distributed random variables with parameter![]() .
.
Theorem 3 Conditioned on![]() , the random variables
, the random variables ![]() have the joint density probability function
have the joint density probability function
![]()
Theorem 4 If ![]() is a random variable associated with the
is a random variable associated with the ![]() event in a Poisson process with parameter
event in a Poisson process with parameter![]() . We assume that
. We assume that ![]() are independent, independent of the Poisson process, and share the common distribution function
are independent, independent of the Poisson process, and share the common distribution function![]() . The sequence of pairs
. The sequence of pairs ![]() is called a marked Poisson process. The
is called a marked Poisson process. The ![]() form a two-dimensional nonhomogeneous Poisson point process in the
form a two-dimensional nonhomogeneous Poisson point process in the ![]() plane, where the mean number of points in a region
plane, where the mean number of points in a region ![]() is given by
is given by
![]()
The marked Poisson processes have been applied in some geometric probability area [3] .
4. Examples of Poisson Processes
1) Suppose the number of calls to a phone number is a Poisson process ![]() with parameter
with parameter ![]() and
and ![]() is the duration of each call. It is reasonable to assume that
is the duration of each call. It is reasonable to assume that ![]() is independent of the Poisson process. What is the probability
is independent of the Poisson process. What is the probability ![]() that the
that the ![]() call gets a busy signal, i.e. it comes when the user is still responding to the
call gets a busy signal, i.e. it comes when the user is still responding to the ![]() call?
call?
For a fixed![]() ,
,
![]()
![]()
2) On average, how many calls arrive when the user is on the phone?
Suppose the user is talking on the ![]() call,
call,
![]()
![]()
3) In a single server system, customers arrive in a bank according to a Poisson process with parameter ![]() and each customer spends
and each customer spends ![]() time with the one and only one bank teller. If the teller is serving a customer, the new customers have to wait in a queue till the teller finishes serving. How long on average does the teller serves the customers up to time
time with the one and only one bank teller. If the teller is serving a customer, the new customers have to wait in a queue till the teller finishes serving. How long on average does the teller serves the customers up to time![]() ? (i.e. How long is the server unavailable?)
? (i.e. How long is the server unavailable?)
![]()
4) Suppose team A and team B are engaging in a sport competition. The points scored by team A follows a Poisson process ![]() with parameter
with parameter ![]() and the points scored by team B follows a Poisson process
and the points scored by team B follows a Poisson process ![]() with parameter
with parameter![]() . Assume that
. Assume that ![]() and
and ![]() are independent, what is the probability that the game ties? Team A wins? Team B wins?
are independent, what is the probability that the game ties? Team A wins? Team B wins?
Let ![]() be the duration of the competition.
be the duration of the competition.
![]()
![]()
![]()
5) Given that there are ![]() points scored in a match (by both team A and team B), what is the probability that team A scores
points scored in a match (by both team A and team B), what is the probability that team A scores ![]() points, where
points, where![]() ?
?
![]()
6) When does a car accident happen? Suppose a street is from west to east and another is from south to north, the two streets intersect at a point![]() . Cars going from west to east arrives at
. Cars going from west to east arrives at ![]() follows a Poisson process
follows a Poisson process ![]() with parameter
with parameter ![]() and cars going from south to east arrives at
and cars going from south to east arrives at ![]() follows a Poisson process
follows a Poisson process ![]() with parameter
with parameter![]() . It is reasonable to assume that these two processes are independent. If the cars don’t slow down and stop at the intersection
. It is reasonable to assume that these two processes are independent. If the cars don’t slow down and stop at the intersection![]() , then collision happens. The
, then collision happens. The ![]() car going from south to north hits the
car going from south to north hits the ![]() car going from south to east if and only if
car going from south to east if and only if![]() , where
, where ![]() is the time it takes for the car's tail to reach
is the time it takes for the car's tail to reach![]() ,
, ![]() has density function
has density function![]() .
.
![]()
![]()
![]()
7) Occurrences of natural disasters follow a Poisson process with parameter![]() . Suppose that the time it takes to recover and rebuild after the
. Suppose that the time it takes to recover and rebuild after the ![]() disaster is
disaster is![]() , assume that
, assume that ![]() are independent random variables having the common distribution functions
are independent random variables having the common distribution functions![]() . There are
. There are ![]() disasters up to time
disasters up to time![]() , what is the probability that everything is back to normal at time
, what is the probability that everything is back to normal at time![]() ? This can also be used as a model for insurance claims.
? This can also be used as a model for insurance claims. ![]() is the time for the insurance company to receive the
is the time for the insurance company to receive the ![]() claim and
claim and ![]() is the time the insurance company takes to settle it. What is the probability that the insurance company is not working on any claim at time
is the time the insurance company takes to settle it. What is the probability that the insurance company is not working on any claim at time![]() ?
?
![]()
where ![]() are independent and uniformly distributed on
are independent and uniformly distributed on![]() .
.
![]()
8) Suppose that ![]() is the time an insurance company receives the
is the time an insurance company receives the ![]() claim and
claim and ![]() is the time the company takes to settle the claim. What is the average time to settle all claims received before time
is the time the company takes to settle the claim. What is the average time to settle all claims received before time![]() ?
?
The average time to settle all claims received before ![]() is
is
![]()
Suppose![]() ,
,
![]()
where ![]() are independent and uniformly distributed on
are independent and uniformly distributed on![]() .
.
![]()
Clearly, ![]() for
for![]() .
.
![]()
9) Customers arrive at a shopping mall follows a Poisson process with parameter![]() . The time the customers spend in the store
. The time the customers spend in the store ![]() are independent random variables having the common distribution function
are independent random variables having the common distribution function![]() . Let
. Let ![]() be the number of customers exist up to the closing time
be the number of customers exist up to the closing time![]() . What is the expected number of customers in the mall at time
. What is the expected number of customers in the mall at time![]() ?
?
Condition on ![]() and let
and let ![]() be the arrival time of the customers. Then customer
be the arrival time of the customers. Then customer ![]() exists in the mall at time
exists in the mall at time ![]() if and only if
if and only if![]() . Let the random variable
. Let the random variable
![]()
Then ![]() if and only if the
if and only if the ![]() customer exists in the mall at time
customer exists in the mall at time![]() . Thus
. Thus
![]()
where ![]() are independent and uniformly distributed on
are independent and uniformly distributed on![]() .
. ![]() is the binomial distribution in which
is the binomial distribution in which
![]()
Hence,
![]()
That is, the number of customers existing at time ![]() has a Poisson distribution with mean
has a Poisson distribution with mean
![]()
The average number of customers exist at the mall closing time is
![]()
10) Customers arriving at a service counter follows a Poisson process with parameter![]() . Let
. Let ![]() be the number of customers served longer than
be the number of customers served longer than ![]() up to time
up to time![]() . What is the distribution of
. What is the distribution of![]() ?
?
Condition on ![]() and let
and let ![]() be the arrival time of the customers. Let the random variable
be the arrival time of the customers. Let the random variable
![]()
Then ![]() if and only if the
if and only if the ![]() customer served longer than
customer served longer than![]() . Thus
. Thus
![]()
which is the binomial distribution with![]() . Hence,
. Hence,
![]()
That is, the number of customers served longer than ![]() has a Poisson distribution with mean
has a Poisson distribution with mean
![]()
5. Conclusion
Poisson process is one of the most important tools to model the natural phenomenon. Some important distributions arise from the Poisson process: the Poisson distribution, the exponential distribution and the Gamma distribution. It is also used to build other sophisticated random process.