Real-Time Modelling of Dynamic Behaviour for Clinker Rotary Kilns: Learning from Experiment and Theory ()
1. Introduction and Background
The Cement Rotary Kiln (CRK) is important equipment used in the chemical, metallurgical industries as well as waste treatment, where it is operated for the continuous process of mixing, heating, incineration, pyrolysis and drying. The basic components of a CRK, (treated as an investigation example) are the steel shell made from a rolled mild steel plate, the refractory material to insulate the steel shell from the high temperatures inside the kiln, a selected burner according to a designed process, supporting tyres and rollers, a driving motor and driving gears. An industrial kiln dimensions can be up to 6 [m] in internal diameter and more than 100 [m] long. Usually it is operated at 1 - 5 [RPM] rotational speed, 1 - 4 [˚] inclination angle and mass flow up to 12,000 [t/d]. A typical CRK with a 3.75 [m] internal diameter and 122.6 [m] long in a clinker production line is shown in Figure 1.
Whether the process is wet or dry, the same chemical reactions take place. Basic chemical reactions are: evaporating all moisture, calcinating the limestone to produce free calcium oxide, and reacting the calcium oxide with the minor materials (sand, shale, clay, and iron). This results in a final black, granular product known as “clinker”.
The study of the particle movement is crucial for the heat transfer from hot gas to the material as well as for process control. Because of the complex nature of the heat transfers, the space varying of the contact surface between the gas, the clinker and the wall is unexplained correctly by using the classical approach. The authors had to find a better way of dealing with this problem. In fact, some of these complex parameters cannot be characterized solely by experimentally measured values. The authors propose an innovative method that creates an intelligent-interface system linking CRK and mainframe computer and capable of working in real-time.
In theoretical approach, some models of the solid flow inside the CRK have been thoroughly investigated by many authors [1] - [14] . Most of them suppose that the CRK parameters are space-invariant. The well-known classical theory of modeling [1] [7] is very useful to investigate the relationship between the temperatures but only in the steady-state conditions. Presently, in modern cement industry, the CRK is often made up of a large number of measured elements, and according to a defined description (see Equations (1) and (2), and Figure 2) the practical investigation [9] - [12] have to be devised to implement numerical simulation techniques. Usually, selected kiln temperatures are very important operational parameters [1] [2] and it is possible to investigate the steady-state conditions by looking at the given relationship between them (see Equations (1) and (2), and Figure 2).
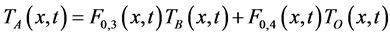 (1)
(1)
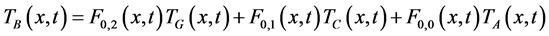 (2)
(2)
where: in particular case, if the CRK is in a steady-state operation,
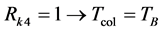 ,
,
![]()
Figure 1. CRK of a clinker production is defined by the five phenomenological zones.
![]()
Figure 2. Equivalent thermal circuit, i.e., the CRK with a clinker attachment.
and
are ambient, shell, brick, clinker and gas temperatures respectively, all 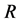 are the thermal resistances of geometry and body, and all
are the thermal resistances of geometry and body, and all 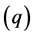 are heat transfers.
are heat transfers.
Once the CRK has been equipped with a system of instrumentations, as the Kiln Shell Temperature Scanner (KSTS), and a few dedicated temperature sensors [12] [15] , then it is possible to estimate the kiln longitudinal temperatures according to the Basic Operating Functions (BOFs), which are
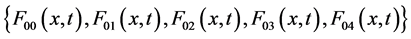 , of the model (see Equations (1) and (2)).
, of the model (see Equations (1) and (2)).
These BOF for the steady-state conditions will be represented by the following forms:
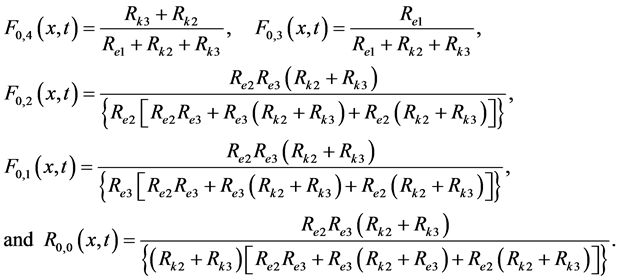
Now the given basic mathematical relationship of the CRK is used as a first step to define the dynamical behaviour which will be represented by a state mathematical model with the space and time-variable parameters [12] [16] .
2. Learning Experiences
The numerical values of the shell and gas temperatures have been collected over two weeks (see Figure 3) to complete the basic data of an operational condition of a full-scale CRK [12] [17] .
As shown in Figure 2 and Equations (1) and (2), the necessary information, estimation and calculation have been used to recreate a particular result of the clinker production process. This computed software has been created, and the computational results have been shown in Figures 4-6.
For the completion of the calculation procedure, by taking into consideration the geometry of CRK, and the longitudinal distribution of the physical phenomena along each zone, the BOFs have been calculated, and the computation can be found in the following diagrams (see Figures 7-9 and Appendix A).
![]()
Figure 3. The shell temperatures taken from a full-scale CRK.
![]()
Figure 4. Reproduced brick temperature profile from the dedicated sensors.
![]()
Figure 5. Reproduced clinker temperature profile from the dedicated sensors.
![]()
Figure 6. Reproduced gas temperature profile from the dedicated sensors.
![]()
![]() (a) (b)
(a) (b)
Figure 9. Estimated BOFs: (a)![]() ; (b) Calculating algorithm.
; (b) Calculating algorithm.
These examples (see Figs. above) illustrate the numerical identification of the BOFs that recreate the steady- state inside temperatures of the CRK (see Figures 4-6).
The author’s objective is to build a uniform mathematical model such as a computer intelligent monitoring system which can reproduce precisely the dynamic behaviour of the CRK with the space and time-variable parameters. In this context, it is necessary that a mathematical structure of a model be described by a set of state equations [9] [12] [16] [17] .
3. Mathematical Structure and Model Concept
Introducing the concept of such a model requires that a small slice ![]() [m] of the CRK is used to establish the heat and mass balance equations [9] [12] [15] -[17] . For this reason, the three state variables, i.e.
[m] of the CRK is used to establish the heat and mass balance equations [9] [12] [15] -[17] . For this reason, the three state variables, i.e.
![]() —Gas, and
—Gas, and
![]() —Clinker temperatures, and
—Clinker temperatures, and
![]() —Mass of clinker [12] [16] in the longitudinal distribution of physical phenomena along the CRK; have been used to create a mathematical structure (MS).
—Mass of clinker [12] [16] in the longitudinal distribution of physical phenomena along the CRK; have been used to create a mathematical structure (MS).
The preliminary investigations [12] [17] were performed to trace these state variable profiles along the real CRK. The gas, the clinker and the shell temperatures have been measured at a number of specific locations in a steady-state condition. In addition, the raw meal input was stopped for an emergency maintenance. This was an exceptional opportunity to estimate the mass of material (clinker)![]() .
.
The resulting profiles, in the steady-state conditions, are shown in Figure 3, Figure 5, Figure 6, and Figure 8.
It is interesting to note that, in the practical operation of CRK, no general procedure exists for determining a set of the classical model parameters [3] [4] [6] [7] . Consequently, the MS suggests [12] [16] [17] that a set of the constant model parameters will be replaced by a set of the space and time-varying Operating Functions (OFs) for which initial conditions are defined as the BOFs (see Appendix A). Thus, a Fundamental Model (FM) for the CRK is:
![]() (3)
(3)
![]() (4)
(4)
![]() (5)
(5)
Consequently, due to nature of the CRK, this system is constructed by a mixed structure including both distributed and lumped subsystems. To establish the frontiers between them, it is assumed that a set of
![]()
is a boundary limit for the kiln which is treated as a distributed subsystem, and the set of
![]()
is a boundary limit for the kiln suppliers treated as a lumped subsystem. Therefore, the analysis of the CRK requires that each state variable must be characterized by its boundary and initial conditions.
When the time derivative of each state equation of the FM, is equal zero, i.e.
![]() (6)
(6)
each steady-state equation of the FM creates an Initial Condition (IC).
In this investigating problem, the steady-state profiles of ![]() are already restored above (see Figure 8) to meet the requirement of all input stabilization.In order to complete the description of the IC, it is necessary to evaluate all OFs (see Figure 1).
are already restored above (see Figure 8) to meet the requirement of all input stabilization.In order to complete the description of the IC, it is necessary to evaluate all OFs (see Figure 1).
Consequently, the fundamental problem when describing the Boundary Conditions (BCs) is to shift an output of the lumped subsystem with an input of the distributed subsystem, i.e., the output of a lumped subsystem becomes the input of a distributed subsystem ![]() for each state equation. It will then be assumed that at these boundaries, only transport phenomena are considered. So, the corresponding BCs for the CRK are presented by the following forms:
for each state equation. It will then be assumed that at these boundaries, only transport phenomena are considered. So, the corresponding BCs for the CRK are presented by the following forms:
![]() (7) (8)
(7) (8)
![]() (9)
(9)
![]() (10)
(10)
In accordance with the description of the BCs, the set of the lumped variables will be treated as the control parameters (LV-CP):
![]()
and
![]()
should be varied to create the optimal conditions inside the CRK. The LV-CV, although treated before as constant, will vary from one time-step to the next in a manner which should be predicted a priori. Additionally, in the optimal operation of CRK, the set of the LV-CV is also called the set of controllability, and will be treated in further research.
For this presentation, (1)-(10) constitute a mathematical model of the dynamic behaviour of the CRK and will be dealt with by a real-time monitoring.
4. Numerical Experiment Evolutions for Standard Air/Fuel Relation
According to the fundamental model proposed by the authors, a simulation procedure consists of a microcomputer-based network of two calculating layers: First: in order to obtain the relationship between the boundary conditions and the resulting state variable profiles, a more elaborate investigation has been proposed, Second: to investigate the local shape of the state variables under various combinations of the Air/Fuel Ration, it was originally suggested to use an analogy of the organization of multi-programmed inputs, which consists of introducing a chemical analyzer into the fuel suppliers and the raw meal supplier.
Now, in the same approach as that of an estimating study of the BOFs (see Figures 7-9), the Standard Air/Fuel Ration (SAFR) has been chosen to obtain the numerical response of FM in the dynamic condition. The simulation tests for the temperature profiles are defined as follows:
Upon examination of the time-space responses of the FM, it can be concluded that using the adjusted OFs (see Appendix B) gives a very good comparison with the measured data. This observation on the model structure (see Figure 10(a) and Figure 11) is rather more interesting than using the classical model [7] [8] [13] .
![]() (a)
(a)![]() (b)
(b)
Figure 10. (a) Temperature reproduced profiles; (b) Distributed mass clinker reproduced profile.
![]() (a)
(a)![]() (b)
(b)
Figure 11. Time-space evolution of the gas and clinker temperatures for SAFR. (a) For gas; (b) For clinker.
5. Conclusions
The paper describes the methodology and estimated results for attempting to build a fundamental model of the CRK which characterizes both the transportation and transformation phenomena. The accuracy of this model is clearly dependent on how correctly and precisely the BOFs have been calibrated. Secondly, the estimation/res- olution of the state variables![]() , which are direct influence on all OFs, is predominant in an identification of the dynamic behaviour of the CRK and useful to adjust all OFs and define a validity horizon of the FM.
, which are direct influence on all OFs, is predominant in an identification of the dynamic behaviour of the CRK and useful to adjust all OFs and define a validity horizon of the FM.
Moreover, once the restored-estimated IC has been evaluated, the desired input (which is treated as the control of the CRK) can be more easily found by the proposed model than by simple trial and error method. Using the state variables approach, it is possible to find adequate measurement points to tune the OFs as the function of restored state variables. In summary, the cooperation and coordination in real-time between industrial computers and the CRK allows for the intelligent monitoring and optimization processes, where each specific set of the control variables must be analyzed by its controllability.
Nomenclature
In general, subscripts have the following meaning:
![]() : Area,
: Area,
![]() : Temperature,
: Temperature, ![]()
![]() : Operating function
: Operating function ![]()
![]() : Heat transfer coefficient
: Heat transfer coefficient
![]() : Specific heat,
: Specific heat, ![]()
![]() : Ideal gas constant,
: Ideal gas constant, ![]()
![]() : Velocity,
: Velocity, ![]()
![]() : Distributed mass,
: Distributed mass, ![]()
![]() : Mass flow rate,
: Mass flow rate, ![]()
![]() : Pressure,
: Pressure, ![]()
![]() : Heat of reaction latent heat,
: Heat of reaction latent heat, ![]()
![]() : Hydraulic diameter
: Hydraulic diameter
![]() : Axial Reynolds number
: Axial Reynolds number
![]() : Angular Reynolds number
: Angular Reynolds number
![]() : Thermal conductivity,
: Thermal conductivity, ![]()
![]() : The angle made by the solid bed at the kiln centre,
: The angle made by the solid bed at the kiln centre, ![]()
![]() : Furnace length,
: Furnace length, ![]()
![]() : The rotational speed,
: The rotational speed, ![]()
![]() : Stefan-Boltzmann constant,
: Stefan-Boltzmann constant, ![]()
![]() : Emissivity
: Emissivity
![]() : Dynamic viscosity,
: Dynamic viscosity, ![]()
![]() : Bulk density,
: Bulk density, ![]()
Subscript
![]() : Primary air
: Primary air
![]() : Secondary air
: Secondary air
![]() : Shell, outer surface of the furnace
: Shell, outer surface of the furnace
![]() : Inner wall of the furnace, refractory bricks
: Inner wall of the furnace, refractory bricks
![]() : Bed material, clinker
: Bed material, clinker
![]() : Gas
: Gas
![]() : Ambient air, air
: Ambient air, air
![]() : Shell, outer surface of the furnace
: Shell, outer surface of the furnace
![]() : Fuel
: Fuel
![]() : Between gas and material
: Between gas and material
![]() : Water vapor, Steam
: Water vapor, Steam
![]() : Water
: Water
Appendix A
The BOFs are decomposed according to the physical parameters of the system and measured state variables (see Figures A1-A5, and Figure B1) according to the physical parameters of the system and measured temperatures
![]()
![]()
Figure A1. ![]() Represented as the links between the thermal resistances and TA & T0.
Represented as the links between the thermal resistances and TA & T0.
![]()
Figure A2. ![]() Represented as the links between the thermal resistances and TA & T0.
Represented as the links between the thermal resistances and TA & T0.
![]()
Figure A3. ![]() Represented as the links between the thermal resistances and TB & TG.
Represented as the links between the thermal resistances and TB & TG.
![]()
Figure A4. ![]() Represented as the links between the thermal resistances and TB & TG.
Represented as the links between the thermal resistances and TB & TG.
Appendix B
B1. Two examples of the OFs which have been decomposed according to the physical parameters of the system and estimated state variables![]()
B2. The numerical solution of the above mentioned FM satisfied the distributed profiles of the space-state variables of the CRK (see Figure 11) with the estimated OFs. According to this approach, the operating functions are:
![]()
Figure A5. ![]() Represented as the links between the thermal resistances and TB & TG.
Represented as the links between the thermal resistances and TB & TG.
![]()
Figure B3. The estimating linear velocity of the clinker.
Analyzing Figure B2 reveals that the OF profiles vary both with time and space-positions across the CRK. For this case the time-response of the FM provides valuable information relating to prescript physical and chemical phenomena. In addition, transferred energy attributed to the motions and configuration of the CRK also varies particularly between two involved temperatures, the heat transfer area, and the attributed chemical reactions. Thus, instead of choosing the constant coefficients in the model, it may be a requirement to opt for the OFs yielding the best possible values.
Examining once again Figure B2, it is possible to say that knowledge of the measured profile of shell temperatures, and restored temperature profiles of the kiln (see Figures 4-6, and Figure 10) are sufficient to estimate all OFs of the CRK as well as the linear velocity of the clinker (see Figure B3).
The results of preliminary tests justify the Newton-Raphson’s method to account for the numerical simulation of all OFs.