A Monte Carlo-Based Approach for Groundwater Chemistry Inverse Modeling ()
1. Introduction
Inverse process models attempt to estimate model parameter values based on changes in observed data between two or more data sets (in contrast to forward process models, which predict the values of variables based on assumed model parameters). In this context, the compositional differences between two groundwater samples—an initial water and a final water, should contain the information necessary for an inverse model to unravel candidate causative reaction and mixing histories. The results of such an inverse model may not necessarily be a uni- que problem exacerbated by uncertainties associated with the groundwater chemistry data itself (e.g., analytical uncertainty, representativeness of samples, incomplete analyses suites).
Different strategies can be employed to address the inverse problem and associated uncertainties. Simple mass and charge balance constraints can be used to determine which reactions are mathematically consistent with the data [1] , although these do not directly test whether or not any particular reaction is thermodynamically favorable. This approach is used in codes such as NETPATH [2] [3] and PHREEQC [4] . PHREEQC’s inverse modeling capability is designed to work with uncertain input in the form of analytical uncertainties associated with each component. Consequently, PHREEQC is able to generate families of inverse models, with associated maxima and minima that can feasibly be contributed by each reaction. Prior studies employing the mass and charge balance inverse modeling approach include [5] , who used PHREEQC’s inverse modeling capability to study the mobilization of arsenic under reducing conditions in groundwater in a shallow aquifer in Arkansas, USA, as well as [6] , who developed a geographical information system (GIS)—an assisted approach coupling a groundwater flow model, and an inverse geochemical model to quantify phase mass transfers involving calcite, dolomite, gypsum, CO2 and fluorite between two points along a groundwater flow path in an Indian aquifer.
An alternative strategy is to utilize a forward-inverse approach that entails running many forward models to identify those reactions that best match the observed data. Least-squares error minimization or similar approaches can be invoked for parameter estimation, a strategy employed by generic inverse models such as CXTFIT [7] [8] and PEST [9] . In the specific context of inverse geochemical modeling, [10] employed a parameter fitting strategy as part of a reactive transport modeling study entailing iron and manganese reduction in coastal aquifers, for example. Nonetheless, while optimization methods can be used to develop a best-fit specific inverse model set from forward models—one that is inherently thermodynamically favored—the uniqueness of the result is still not assured. The optimization routine employed may simply identify a local minimum of whatever error function is being minimized and thus may fail to return better estimates of a global minimum, or, alternatively, multiple sets of objective function minima encompassing a broad sample of the parameter space. Additional information can be gleaned from the data by conducting Monte Carlo simulations to systematically sample the parameter space. However, such a brute-force Monte Carlo approach can be inefficient in identifying an optimal parameter set which reproduces the measured data with sufficient fidelity.
To address these issues, a modified Monte-Carlo-based geochemical modeling strategy is proposed to constrain the parameter space search. The strategy is based on the Metropolis-Hastings algorithm [11] , a Markov- Chain-based technique for approximating probability distributions of parameter values that minimize or maximize a multi-parameter objective function. The Metropolis-Hastings Monte Carlo (MHMC) approach is particularly useful for understanding inverse model parameter probability distributions in cases where those distributions are poorly understood a priori. This is often an issue for groundwater geochemical models, where various aqueous components and phases can interact with one another through a large number of aqueous complexation reactions, electron transfer reactions, surface reactions, and other mechanisms, sometimes obscuring simple relationships between model input and model output. Reference [12] employed a MHMC strategy to quantify water-rock reactions along a flow path in a carbonate system with simple mineralogy. In this current study, a more general geochemical modeling approach is considered, with example applications that include inverse modeling of groundwater interactions with a granitic rock mineral assemblage and an assessment of the impact of fuel hydrocarbon bioattenuation on groundwater chemistry.
2. Methods
The MHMC strategy involves the sequential generation of sets of proposed parameter values, submission of those values as input into a forward model, and quantification of the resulting goodness-of-fit of the model output to the data through a scoring scheme. The approach is iterative in nature in that the current score for a given iteration is compared with the score from the prior run; if the goodness of fit using the current parameter set represents an improvement, the proposal is automatically accepted. Proposals that score poorly in comparison are not necessarily rejected, however, provided that the proposal scores above some threshold fraction (typically chosen at random) of the prior score. This strategy prevents the algorithm from prematurely converging on local minima or maxima, allowing for more complete exploration of the parameter space but with a bias towards more promising parameter combinations. The parameter set values themselves are selected as part of a Markov Chain sequence; each new proposal represents only relatively minor changes in postulated values in comparison to the prior set. Rejected proposals result in a subsequent new set of posited parameter values using the previous “seed” values, whereas the parameter values associated with accepted proposals are assigned as the new seed values for the next iteration.
The overall algorithm for the application of the MHMC strategy to the generation of an inverse geochemical model is summarized in Figure 1. A given inverse problem is first defined by an initial, or ambient water composition, and a final composition. One or more aqueous components must be present in both solutions to permit differences to be quantified. Reactions that could explain these differences can include: 1) mass transfer between the solution and mineral or gas phases; 2) electron transfer (i.e., oxidation-reduction); 3) ion exchange; 4) surface complexation; 5) evaporation. In addition, mixing of a third water composition—added to the ambient water composition and thus contributing to the final composition can also be considered. Specific parameters that define the nature of these reactions but may represent unknown quantities include masses of mineral phases or gases initially present in the model and their dissolution equilibrium constants (if subject to some uncertainty), the quantity of an ion exchanger present (the equivalent of cation exchange capacity), the amount of water evaporated from the ambient solution composition, and the quantity of any third water composition mixed with the ambient water. Once constraints on each of the parameter ranges are prescribed, a generator algorithm can define the input for a forward geochemical simulation as a trial for a given proposal.
![]()
Figure 1. The Metropolis-Hasting Monte Carlo (MHMC) algorithm, as applied to an inverse groundwater geochemical problem.
After a proposal is run as a forward geochemical model, the resulting concentration predictions must be compared to the corresponding measured concentrations in the final water composition for each of the selected metrics. A useful definition of a proposal’s score is a lumped sum of the squares of the errors for each metric component, defined logarithmically:
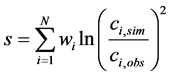 (1)
(1)
where N is the number of water quality metrics, csim and cobs the simulated and observed concentrations, respectively, and w a weighting factor introduced to provide some flexibility in emphasizing the importance of matching certain metrics with respect to others (any such intentional bias will be application-specific).
The MHMC algorithm accepts any proposal yielding a score that is less than that of the prior proposal, with scores that do not meet this requirement accepted only conditionally. Specifically, proposals with higher scores than the prior trial are accepted when the inequality,
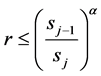 (2)
(2)
is satisfied, where r is a random number selected between 0 and 1, 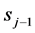 and sj the prior and current scores. The exponent α serves as a means to throttle the proposal acceptance rate and is selected by trail-and-error for specific applications; an acceptance rate between 0.3 and 0.7 generally leads to quicker convergence to viable distributions of model parameter values.
and sj the prior and current scores. The exponent α serves as a means to throttle the proposal acceptance rate and is selected by trail-and-error for specific applications; an acceptance rate between 0.3 and 0.7 generally leads to quicker convergence to viable distributions of model parameter values.
PHREEQC was employed as the forward model in the MHMC algorithm. A python script was used to automate the generation of posited parameter sets for each iteration, write the input file for PHREEQC, execute PHREEQC, and subsequently read, process, score, and record the resulting output.
3. Results
3.1. Sierra Spring Water
A geochemical inverse model example described by [13] is provided with the PHREEQC software package. The example consists of two sets of spring water data collected in the Sierra Nevada range in California, USA: water from an ephemeral springs and water from a perennial spring. Both waters are assumed to have been in contact with a mineral assemblage consisting of silica, plagioclase (as Na0.62Ca0.38Al1.38Si2.62O8), biotite mica (as KMg3AlSi3O10(OH)2), kaolinite, montmorillonite (as Ca0.17Al2.33Si3.67O10(OH)2), calcite, halite, gypsum, and CO2. The perennial spring sample is characterized by higher concentrations of major cations and anions (e.g., Na, Ca, Mg, HCO3, SO4) than the ephemeral spring sample, an observation consistent with presumed differences in residence time (Figure 2). The inverse modeling capability of the PHREEQC code itself suggests that the compositional differences between the two waters can be largely explained by additional dissolution of CO2, calcite, in the perennial spring water, coupled with the precipitation of kaolinite and silica. Because PHREEQC’s inverse model considers compositional uncertainty in the measured data, two different possible inverse models are indicated (Figure 3).
The MHMC inverse model for the Sierra Spring water problem assumes a set of phases included in PHREEQC’s thermodynamic database (phreeqc.dat) that approximately correspond to the mineralogy specified in the example problem. This assemblage includes calcium montmorillonite (characterized by the same stoichiometry as the PHREEQC inverse modeling example), kaolinite, and chalcedony as the silica phase. A K- mica phase, KAl3Si3O10(OH)2, was used as a surrogate for the biotite mica assumed by the PHREEQC inverse model example (for which an equilibrium constant was not specified). Unlike the example mica, this K-mica phase does not contain any magnesium, so magnesium was not included as a metric for scoring the proposal. Plagioclase was modeled as an ideal solid solution consisting of albite, NaAlSi3O8, and anorthite, CaAl2Si2O8, end-members, with an initial Na:Ca ratio of approximately 2:1. In addition to this Na:Ca ratio, other uncertain model parameters included initial masses of kaolinite and K-mica as well as equilibrium constants for calcium montmorillonite and K-mica. Search ranges for the initial mineral masses were lognormally distributed between 10−6 and 10−3 moles/kgw, while uncertainties in the equilibrium constants were addressed by specifying a log saturation index constraint for mineral precipitation/dissolution in the PHREEQC input files between −0.25 and +0.25.
A total of 5000 trial proposals were evaluated, requiring several minutes of run time on a Windows-based personal computer, with the score contribution weighting factors for all components set equal to 1.0 except for Na and pH, for which weighting factors were set to 5.0 and 10.0 to improve the rate of convergence. Approximately 37 percent of the proposals were accepted. Matches of the MHMC inverse algorithm results to the water quality data are shown in Figure 2. The mineralogical changes associated with the best-case proposals (e.g., those with the lowest composite scores) for both scenarios are compared to the PHREEQC inverse model in Figure 3. The model matches the concentration data well except for the concentration of potassium, which remains unchanged because the K-mica phase is not favored to dissolve, a reflection of its particular stoichiometry and dissolution equilibrium constant, and magnesium, which is excluded. Mass transfer reactions are qualitatively consistent with the results of PHREEQC’s inverse model in a broad sense in that halite, gypsum, calcite, gas-phase CO2, and plagioclase all dissolve into solution by approximately corresponding amounts. However, the remaining silicate phases exhibit somewhat different behavior in that Ca-montomorillonite is favored to dissolve. This dissolution reaction contributes to the precipitation of both kaolinite and chalcedony in quantities that exceed those yielded by the PHREEQC inverse model results.
![]()
Figure 2. Measured concentrations of groundwater solution constituents compared with forward-model best-proposal results (i.e., minimal weighted error scenario) of the MHMC algorithm.
![]()
Figure 3. Mass transfer reactions consistent with observed differences between the Ephemeral and Perennial spring water compositions. The two PHREEQC inverse model results reflect ideal mass balances, within prescribed analytical uncertainties, but are not explicitly constrained by thermodynamic considerations. The best-proposal MHMC result—the minimum-error forward model realization, is thermodynamically valid but does not guarantee mass balance with respect to the data.
While the results of the only the best-fit proposal are shown in Figure 1 and Figure 2, the MHMC approach is designed to furnish approximations to the probability distributions for individual constituents about the optimal solution. The distribution of initial calcite mass among the best-scoring 100 proposals is shown in Figure 4 (all of the initial calcite mass in all of these proposals dissolves completely in the respective forward models). The probability distribution used by the proposal generator assumed, purely as a trial basis, that the initial calcite mass ranges between 10−6 and 10−3 moles/kilogram of water, characterized by a lognormal distribution (log mean = 3.2 × 10−5 mol/kgw). The MHMC-derived distribution shown in Figure 4 differs appreciably from this prior distribution and thus represents a refined estimate over the postulated initial range of reacted calcite mass.
3.2. Fuel Hydrocarbon Bioattenuation and Trace Element Mobilization
A second demonstration application concerns the impact of fuel hydrocarbon bioattenuation on groundwater chemistry at an anonymous site in Montana, USA, where impacts to groundwater by diesel from a leaking above-ground tank are known to have occurred. Inverse modeling entailed using a limited site quality data set to assess consistency of the data with bioattenuation and to quantify hydrocarbon mass reduction to support remedial planning. Groundwater quality data measured in site groundwater wells includes manganese, ferrous iron, sulfate, sulfide, methane, bicarbonate alkalinity, chloride, and trace elements of potential environmental concern, in addition to dissolved-phase diesel fuel, reported as total petroleum hydrocarbons (TPH). In contrast, general indicators of groundwater quality, such as major cations and pH, have not been subject to monitoring.
Processes that are commonly observed to occur in association with bioattenuating organic matter or fuel hydrocarbons, such as reduction of ferric iron and sulfate as well as methanogenesis [14] [15] , are suggested by spatial variability in historic site groundwater data. In addition, arsenic and barium concentrations are also locally elevated in site groundwater in apparent association with dissolved fuel hydrocarbons. The MHMC algorithm was used to identify a set of mass and electron transfer reactions that could consistently explain the observed differences in groundwater chemistry between hydrocarbon-impacted and non-impacted (i.e., “background”) groundwater from a recent (2013) groundwater sampling event. The background groundwater composition was defined by the median concentrations of the constituents of interest (bicarbonate alkalinity, arsenic, barium, iron, methane, sulfate, and sulfide) among those groundwater samples characterized by the absence of TPH below the detection limit of 10 µg/L, representing a total of twelve wells. The impacted groundwater sample composition was defined by the median concentrations of the same constituents in six wells characterized by TPH concentrations in the uppermost quartile of wells with positive TPH detections, equivalent to a threshold concentration of approximately 300 µg/L.
Both dissolved iron and manganese were detected in nearly all groundwater samples collected from the site, including background samples. Consequently, PHREEQC was used to set the initial redox potential to reflect equilibrium with goethite, FeOOH (manganese geochemistry was not included in the inverse modeling assessment). Ferrihydrite, Fe(OH)3, is an alternative ferric oxide mineral choice, although trial simulations indicated it
![]()
Figure 4. Representation of the probability distribution of calcite mass transferred into solution for the Sierra spring water example, implied by the best 100 scoring proposals among those accepted from the 5000-trial MHMC simulation.
was much less effective in matching the observed data. Goethite was also designated as a reactive hydrous ferric oxide surface (HFO) vis-à-vis PHREEQC’s surface chemistry modeling feature. The HFO surface was assumed to be in equilibrium with background groundwater chemistry as an initial condition. This specification fixed the total amount of arsenic in the system, with the majority of the arsenic mass existing in a sorbed state on the HFO (arsenic was modeled as existing only in the arsenate form, i.e., the +V redox state). Additional phases included in the model were barite (BaSO4), calcite (CaCO3), and mackinawite (FeS). Diesel was represented in the model by a mean stoichiometry of C12H23.
A total of 5000 proposals were generated and assessed using the MHMC algorithm, of which 1816 proposals, or approximately 36 percent, were accepted. A comparison of median measured background and impacted biodegradation constituents and the forward-model output generated by the best-scoring proposal is shown in Figure 5. The best-scoring model results match the differences in the observed data well in a semi-quantitative sense; mismatches are likely attributable to spatial variability in both background groundwater composition and the extent to which various bioattenuation mechanisms vary locally. Nonetheless, despite the lack of a comprehensive suite of analytes fully characterizing the groundwater chemistry at the site, the MHMC results indicate that the available bioattenuation indicator data alone is consistent with the transformation of a particular quantity of hydrocarbon material, assuming equilibrium constant values that are consistent with the thermodynamic data.
The sensitivity of the accepted proposal scores to two key parameters—the initial mass of diesel and the initial mass of goethite are shown in Figure 6 and Figure 7, respectively. The initial mass of diesel added is well- constrained among the best-scoring proposals, indicating the threshold mass required to bring about removal of the majority, but not the entirety, of sulfate via reduction. In contrast, the initial mass of goethite, while clearly exerting an effect on the proposal score through impacts on dissolved iron, sulfide (via FeS precipitation), and arsenic concentrations, is characterized by a wider distribution of values for best-scoring proposals.
In addition to the posited initial masses, equilibrium dissolution constants (represented in proxy by fixing the logarithm of the saturation index for the mineral phase) for mineral phases with presumably uncertain composition—hydrous ferric oxide and iron sulfide were also treated as unknowns and thus allowed to vary within certain ranges in the proposal parameter sets. Among the top ten scoring proposals, log saturation indices for the iron oxyhydroxide phase, goethite), ranged between +1.2 and +1.8; that of the best proposal was approximately +1.5. In effect, this represents an intermediate solubility between that of goethite and the more soluble phase Fe(OH)3, as represented in PHREEQC’s database but not considered in the inversion. Saturation indices among the top ten proposals for FeS phase (mackinawite) ranged between +1.0 and +1.4, with that of the best proposal at approximately +1.3. Analogous to the iron oxyhydroxide phase, this value corresponds to an intermediate solubility between mackinawite and the more soluble amorphous FeS precipitate phase represented in the phreeqc.dat database of the PHREEQC code but not included in the model.
![]()
Figure 5. Comparison of median background, impacted and modeled concentrations (best-proposal score MHMC result) for fuel hydrocarbon bioattenuation indicators in groundwater.
![]()
Figure 6. Association of proposal composite score with posited initial diesel (idealized as C12H23) mass loading to the modeled solution, per accepted MHMC proposal.
![]()
Figure 7. Association of proposal composite score with posited initial FeOOH mass in contact with solution, per accepted MHMC proposal.
4. Conclusion
The goal of the MHMC strategy is to identify approximate probability distributions of model parameters that best reproduce observed data. In principle, employing ever larger numbers of iterations should yield increasingly accurate approximations, assuming that the underlying forward model is itself applicable. For the geochemical inverse modeling approach proposed in this study, the forward model PHREEQC has already been well vetted elsewhere in the literature. Therefore, the best-scoring proposals generated by the MHMC algorithm, employing a large number of iterations, can be regarded as providing insights that are consistent with respect to mass balance, charge balance, electron transfer, and thermodynamic considerations. In this context, the MHMC approach serves to safeguard against inverse models that contain spurious mass transfer reaction sets that should not otherwise occur, a threat that exists with approaches such as PHREEQC’s built-in inverse modeling tool. However, some limitations of the MHMC approach, as proposed, should be considered. Clearly, the validity of its application to any specific problem should always be assessed on a case-by-case basis, requiring consideration of mineral phase selection and the reliability of thermodynamic data. Second, the geochemical inverse modeling does not take into account the reaction path followed by the system as one water composition is transformed into another; only the initial and final solution states are addressed (i.e., reaction kinetics are not addressed).