The Periodic Solitary Wave Solutions for the (2 + 1)-Dimensional Fifth-Order KdV Equation ()
1. Introduction
The soliton equations play a very important role in the study of nonlinear phenomena in different fields such as the fluid physics, nonlinear optics, plasma physics and so on [1] [2] . The researches on the explicit analytic solutions for the soliton equations can help understand the nonlinear dynamics better. With the development of soliton theory, there are many systematic approaches solving different kinds of soliton solutions, such as the inverse scattering transformation [1] [2] , the Darboux transformation [3] , the variable seperation method [4] , the bilinear method and so on [5] -[7] . Among those methods, the bilinear method is a powerful and direct approach to find soliton solutions for the nonlinear partial differential equations. Besides the soliton solutions, Dai has presented that the periodic solitary wave solutions for the soliton equations can be obtained by suitable test functions using the bilinear form [8] .
In this paper, we will consider the (2 + 1)-dimensional fifth-order KdV equation
(1)
with
, which is a (2 + 1)-dimensional analogue of the Caudrey-Dodd-Gibbon-Kotera-Sawada (CDGKS) equation [9] . When
, it can be reduced to the CDGKS equation. Equation (1) was first proposed by Konopelchenko and Dubovsky [10] [11] . In Ref. [12] , the quasi-periodic solutions for Equation (1) have been obtained in terms of the Riemann theta functions. The symmetry transformations for Equation (1) have been given based on its Lax pair [13] . In this paper, with the help of symbolic computation, some novel periodic solitary wave solutions for Equation (1) will be derived based on the bilinear form.
2. Bilinear Form
According to the leading order analysis in the Painlevé test, we can find the dependent variable transformation for Equation (1),
, (2)
with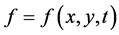
. Substituting Transformation (2) into Equation (1), the following bilinear form can be obtained,
, (3)
where
, 
and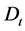 
are the bilinear derivative operators [14] defined as,
.
3. Periodic Solitary Wave Solutions
In this section, according to different test functions for
, we will derive the periodic solitary wave solutions for Equation (1).
3.1. Single Periodic Solitary Wave Solutions
Taking 
in Equation (3) as the following form
. (4)
Substituting Solution (4) into the bilinearized equation (3), and equating the coefficients of different triangle and exponential functions to be zero, we can obtain the following equations,
, (5)
, (6)
, (7)
, (8)
, (9)
, (10)
(11)
Solving the above system, two sets of single periodic solitary wave solutions can be got.
Case 1:
, 
, 
, 
, 
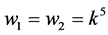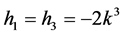Denoting
, 
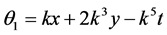then
. (12)
with 
and 
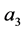are arbitrary constants. Substituting 
into the transformation (2), we can obtain the single periodic solitary wave solution
. (13)
Case 2: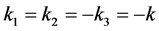
, 
, 
, 
, 
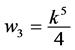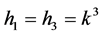Denoting
, 
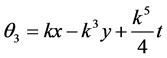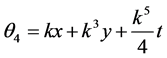then
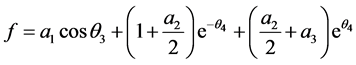, (14)
with 
and 
are arbitrary constants. Substituting 
into the transformation (2), the following single periodic solitary wave solution can be obtained,
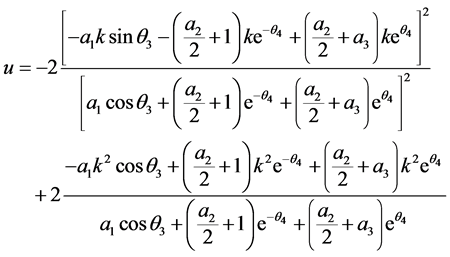. (15)
3.2. Two Periodic Solitary Wave Solutions
Taking 
as the following form
. (16)
Substituting 
into the bilinearized equation (3), and equating the coefficients of different triangle and exponential functions to be zero, we can obtain the following equations,
,
,
,
,
,
,
.
Solving the above equations, we can obtain some novel two periodic solitary solutions of Equation (1).
Case 1: 
Denoting
, (17)
then
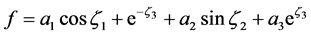, (18)
with 
are arbitrary constants. Substituting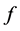 
into the transformation (2), we can obtain the two periodic solitary wave solution
. (19)
Case 2:
, 
, 
, 
, 
Denoting
, 
, 
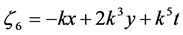then
. (20)
with 
are arbitrary constants. Substituting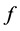 
into the transformation (2), we can obtain the two periodic solitary wave solution
. (21)
Case 3: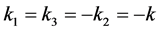
, 
, 
,
, 
, 
,
which can give two sets of solution. Denoting
, 
,
.
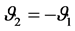Then 
can be obtained in the following form,
, (22)
According to Transformation (2), we can yield another two periodic solitary wave solutions for Equation (1).
4. Conclusion
As the important (2 + 1)-dimensional higher-order generalization of the KdV equation, the solutions for the (2 + 1)-dimensional fifth-order KdV equation are good at understanding the nonlinear phenomena in the fluid dynamics. In this paper, the bilinear form for such an equation is derived based on a logarithm transformation. And then, by choosing two kinds of test functions, we have derived six new sets of periodic solitary wave solutions and verified them using the symbolic computation. It is hoped that the results obtained in this paper can be of help for the study of (2 + 1)-dimensional fifth-order KdV equation and the potential real application.
Acknowledgements
This work has been supported by Beijing Excellent Talent Training Project (2013D005007000003), the Scientific Research Project of Beijing Educational Committee (No. SQKM201211232016) and the National Natural Science Foundation of China under Grant No. 61072145.