Prediction of the Elastic Properties of Short Basalt Fiber Reinforced Al Alloy Metal Matrix Composites ()
1. Introduction
Metal matrix composites (MMCs) reinforced with discontinuous phases in the forms of short fibers, whiskers, and particulates exhibit considerably enhanced strength values at room temperature or at higher temperatures, low coefficient of thermal expansion, good wear resistance and stiffness compared to the corresponding unreinforced alloys [1]. Discontinuous fiber reinforced composite forms an important category of materials used in engineering applications. The metal-matrix composites offer a spectrum of advantages that are important for their selection and use as structural materials. A few such advantages include the combination of high strength, high elastic modulus, high toughness and impact resistance, low sensitivity—to changes in temperature or thermal shock, high surface durability, low sensitivity to surface flaws, high electrical and thermal conductivity, minimum exposure to the potential problem of moisture absorption resulting in environmental degradation, and improved fabricability with conventional metal working equipment [2].
Fiber reinforced composites consist of fibers of high strength and modulus embedded in a matrix with distinct interfaces between them [3]. Fiber reinforcement improves the stiffness and the strength of the matrix. In the case of polymers that are not tough in the non-reinforced form, the toughness may also increase. The fibers reinforced composites exhibit anisotropy in properties. The maximum improvement in mechanical properties is obtained with continuous fiber reinforcement. However, short fiber reinforced composites offer many advantages like ease of fabrication, low production cost and possibility of making complex shaped articles, over continuous fiber reinforcement [4]. The performance of the composite is controlled by the fibers and depends on factors like aspect ratio, orientation of fibers and fiber-matrix adhesion. In the case of short fiber reinforced MMCs, not only random arrangements of fibers but also their random orientations are observed and their mechanical properties are highly dependent on their composition, the matrix, as well as the type and weight percentage of reinforcements [4]. The complexity of such affecting parameters makes a complete theoretical description of the elastic behaviour and the failure properties of short fiber reinforced composite with metal matrix nearly impossible. In this respect a micromechanical analysis of the local composite failure process opens a possibility to predict the failure property of composites [5-8].
In the literature, the effect of fiber length and fiber orientation on mechanical properties of discontinuous fiber composites has mainly been investigated for short fiber composites (characterized by an average fiber length less than 1 mm) [9-11]. The majority of the micromechanical models take into account the fibre orientation distribution, but can only predict a lower and sometimes only an upper bound for a limited number of engineering constants, mainly Young’s modulus. This is insufficient for further development of damage prediction. Moreover, the interaction between the oriented fibres is not always considered in those models. Chen et al. [12] proposed a model based on Eshelby-Mori and Tanaka theory including the interaction between misaligned fibres but only for planar orientation distribution and transversely isotropic distribution of fibres. Their model uses the distribution function developed by Kacir et al. [13] assuming planar orientation, which has the capability to describe either unidirectional distribution or random planar distribution.
The elastic behaviour of short fiber reinforced composites is complex and the present knowledge of elastic modulus study still needs extensive investigation of the micromechanical composite behaviour. The effect of short fibers as reinforcement in metallic matrixes can be clarified with the help of a micromechanical model. The micro-mechanical model presented in this paper is an adaptation of the model developed first by Huysmans [14] and improved by Tsujikami [15], based upon transformation strain concepts for the prediction of the elastic behaviour of textile reinforced composites. The same modelling approach is used in the elastic model for short fiber composites, only the geometrical description of the composite material is different. Software was developed, based on the Mori and Tanaka method, shear-lag, computational model, Nielsen-Chen model and Miwa’s model, to predict a single estimation of a set of stiffness constants rather than an upper and lower bound, taking into account the microstructure of the part. In the present study, computational model developed was used to compare the elastic modulus of a short-Basalt fiber reinforced MMCs with experimental results by using a computer software.
2. Experimental Work
The matrix alloy used in the present investigation was Al 7075 alloy, which has basalt short fiber reinforcement and chemical composition is as shown in Table 1. Fibers in roving form were bundled and cut into short fibers of uniform length by constant-length cutter. The short Basalt short fiber was cleaned in distilled water and dried at 90˚C.
Composites were fabricated using a liquid infiltration method (squeeze infiltration technique) described by Akbulut et al. [16]. A fiber preform of diameter 10 mm and 80 mm long was placed in a die preheated to 350˚C and infiltrated with liquid metal. Al alloy was superheated by about 100˚C and injected by means of a ram travelling at about 9 mm·sec−1, with a pressure setting of 25 to 30 Mpa to the mould. The specimen was obtained after cooling the mould rapidly. The specimens (70 mm long and 6 mm diameter) were precision-machined from the cylindrical blanks with a diamond tipped cutting tool as per ASTME-817 [17] standards. The test was performed using a Shimuzu universal testing machine (of 10 tons capacity) equipped with a pair of extensometers. The modulus measurements were carried out on the specimens in tension, using “loading unloading method” with a crosshead velocity of 5 mm/min. Young’s modulus values were calculated from the slope of the ruler fit straight lines joining the two ends of the loading-unloading curves. Finally the UTS were calculated for the same specimen. This test was repeated at least four times using different specimens and the mean values and corresponding standard deviation were obtained.
The choice of a sample for microscopic study is very important for analyzing composites. Optical microscopy was used to examine the general microstructure and fiber distribution in the composite produced. To increase the visibility of the embedded fibers in the matrix, the composites were etched deeply with Palmerton etching reagent [18] (Chromicoxide—200 g, Sodium sulfate—15 g, water—1000 ml). Scanning Electron Microscopy (SEM)

Table 1. Chemical composition of Al alloy & short basalt fiber.
was performed on the fractured surface to understand the failure mechanisms.
3. Results and Discussion
3.1. Modeling
Rapid advances made in hardware & software technological fields have fundamentally changed our environment. Mathematical models are designed increasingly to support decision-making processes. Composite materials can be fabricated by choosing different combinations of matrix alloy and reinforcements. For MMCs, the matrix is usually an alloy based material and there are also an increasing number of available reinforcements, e.g., fibers, particulates, whiskers, etc. Regarding the prediction of properties of MMCs from the properties of the individual components, numerous mathematical modeling techniques have been formulated. Each model is bound by a set of parameters and also the data is specific for successful evaluation. There are an extremely large number of different MMCs, each having different individual properties. The reinforcement can be of a variety of types, having undergone different surface treatments, their range of weight % are also varied, they may possess different geometries (such as particles, whiskers short fiber and long fiber). The enormous number of different MMCs (matrix and reinforcement) has lead to significant problems in manufacturing and testing activities the manufacturing processes adopted are very expensive. In addition to quantitative analysis of the properties of the MMCs mathematical modeling also helps to estimate cost of essential development and can be used in the design of MMCs to meet specific requirements. All existing tensile models are based on the same basic assumptions, such as the matrix is linearly elastic and isotropic. The fibers are identical in shape and size but they are either isotropic or transversely isotropic. There is a perfect interfacial bonding between the matrix and the fibers, there is also a nearly perfect bonding at their interface, and there is no chemical reaction between them [19].
3.2. Elastic Modulus
The reinforcement may be regarded as acting efficiently if it carries a relatively high proportion of the externally applied load. This results in higher strength, as well as greater stiffness, because the reinforcement is usually stronger, as well as stiffer, than that of a matrix. The concept of elastic load transfer is familiar for those who are working with fiber reinforced composites [20]. In general, the shear-lag model equation is most appropriate to estimate the elastic properties of the aligned short fiber reinforced composites. It is not possible to produce composite specimens with perfectly aligned fiber. Therefore the author prefers computational model to compare the elastic modulus of a short-Basalt fiber reinforced MMCs with experimental results by using a computer software. The author compared computational model with the Nielsen-model, which assumes approximate elastic properties of the random short fibers reinforced MMCs.
3.3. Shear-Lag Model
Originally, Shear-lag model was developed by Cox. Cox was the first to examine [21] the continuos fiber MMCs. A detailed derivation was summarized by Kelly [22], and this model is best well suited for short fiber MMCs in which short fibers of uniform length and diameter are all aligned in the loading direction and distributed uniformly throughout the material as shown in Figure 1. The elastic modulus of the composite Ec and fiber length l, and detailed the derivations of shear-lag model [23].
 (1)
(1)
where Em and Ef are the Young’s modulus of the matrix and the fiber respectively, Vf is the weight percentage of the fibers, and b is a matrix material constant [24].
 (2)
(2)
Gm is the shear modulus of the matrix, with a fiber diameter d and D is the diameter of the unit cell, which is a function of the fiber weight percentage and fiber diameter d. Accurate experimental data is not available, since it is not possible to produce physical samples with perfectly aligned fibers. The main drawback of this model is that it estimates elastic properties only when fiber aligns to the loading direction of the composite. But in practice, in short fibers reinforced composites; the fibers are not aligned in the direction of the applied load. Considering this parameter, the authors-computational model (Figure 2) has been developed.
 (3)
(3)

Figure 1. Shear-lag model for aligned short fiber composite.
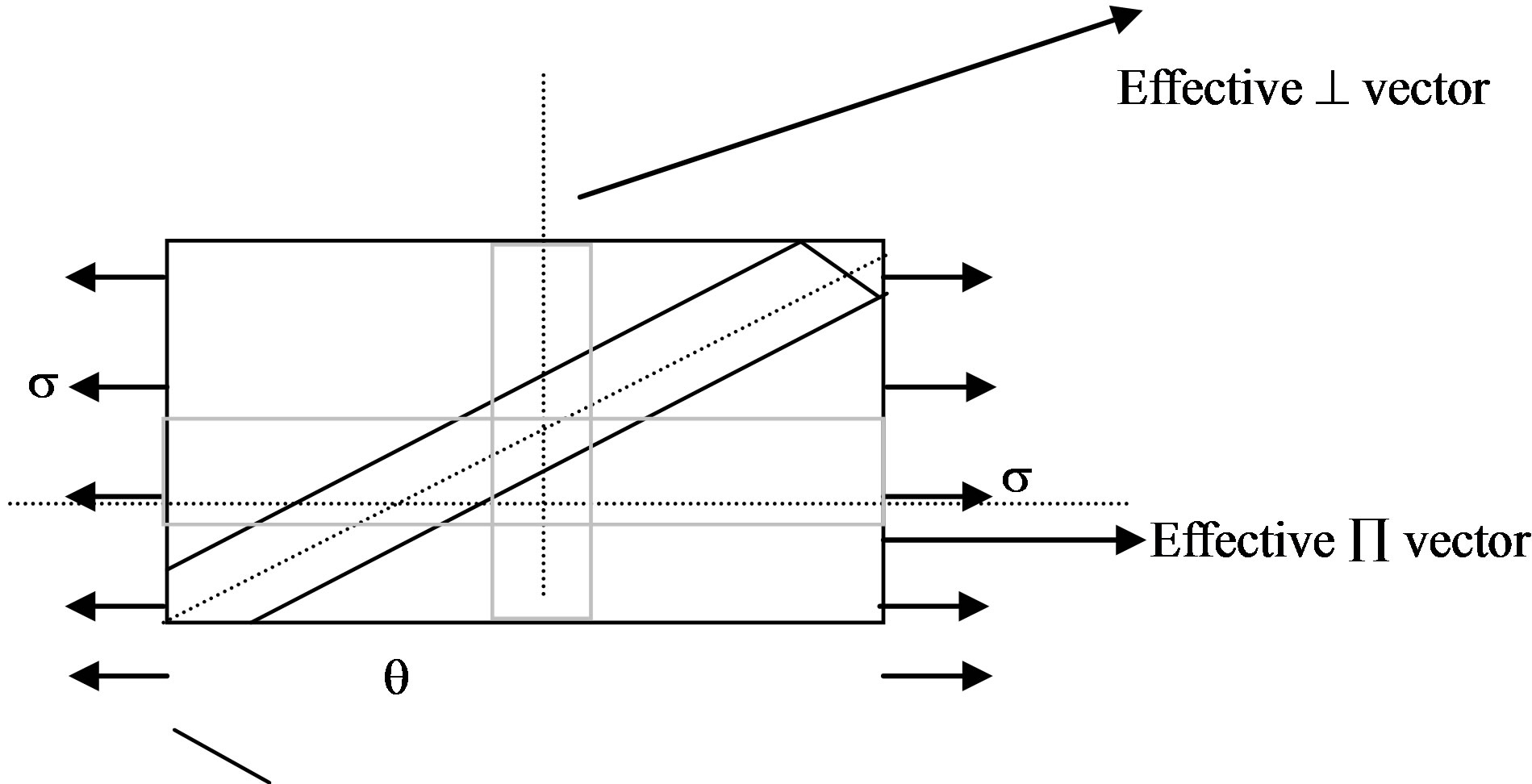
Figure 2. Short fiber inclined at an angle (q) to the loading direction.
In which q is the effective angle between the fiber axis and the axis of the matrix. Considering the effective angle of fiber, Young’s modulus can be resolved into two components that is, (EÕ) young’s modulus parallel to the axis of loading direction and (E^) perpendicular to axis of loading. EÕ and E^ were obtained from the rule of mixture equation. From the mixture rule (upper bound)
[25]
 (4)
(4)
From the mixture rule (lower bound) (Ref 25)
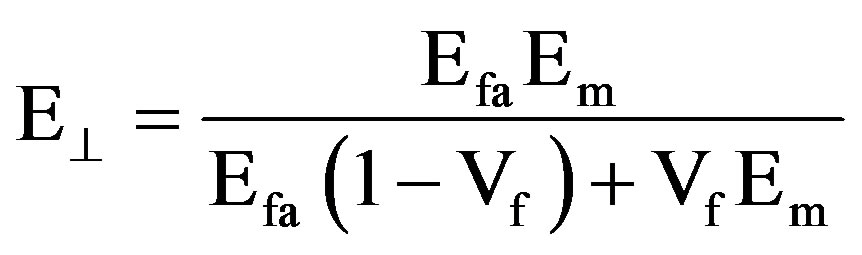 (5)
(5)
The Young’s modulus of the short fiber reinforce composite is given by
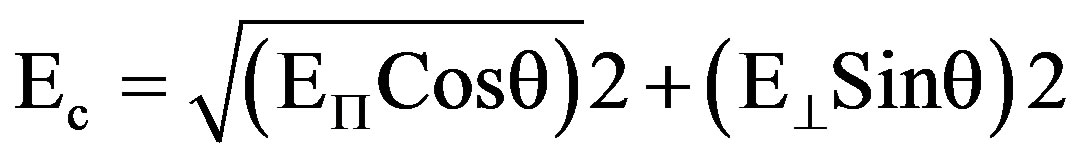 (6)
(6)
The effective angle of the fibers (q) was computed by using the software developed by the author which is shown in the form of a flowchart (Figure 3). From this software, the effective fiber angle q = 161.83Vf0.4027 was obtained.
3.4. Nielsen-Chen Model
Bert (25) has given another model describing the elastic
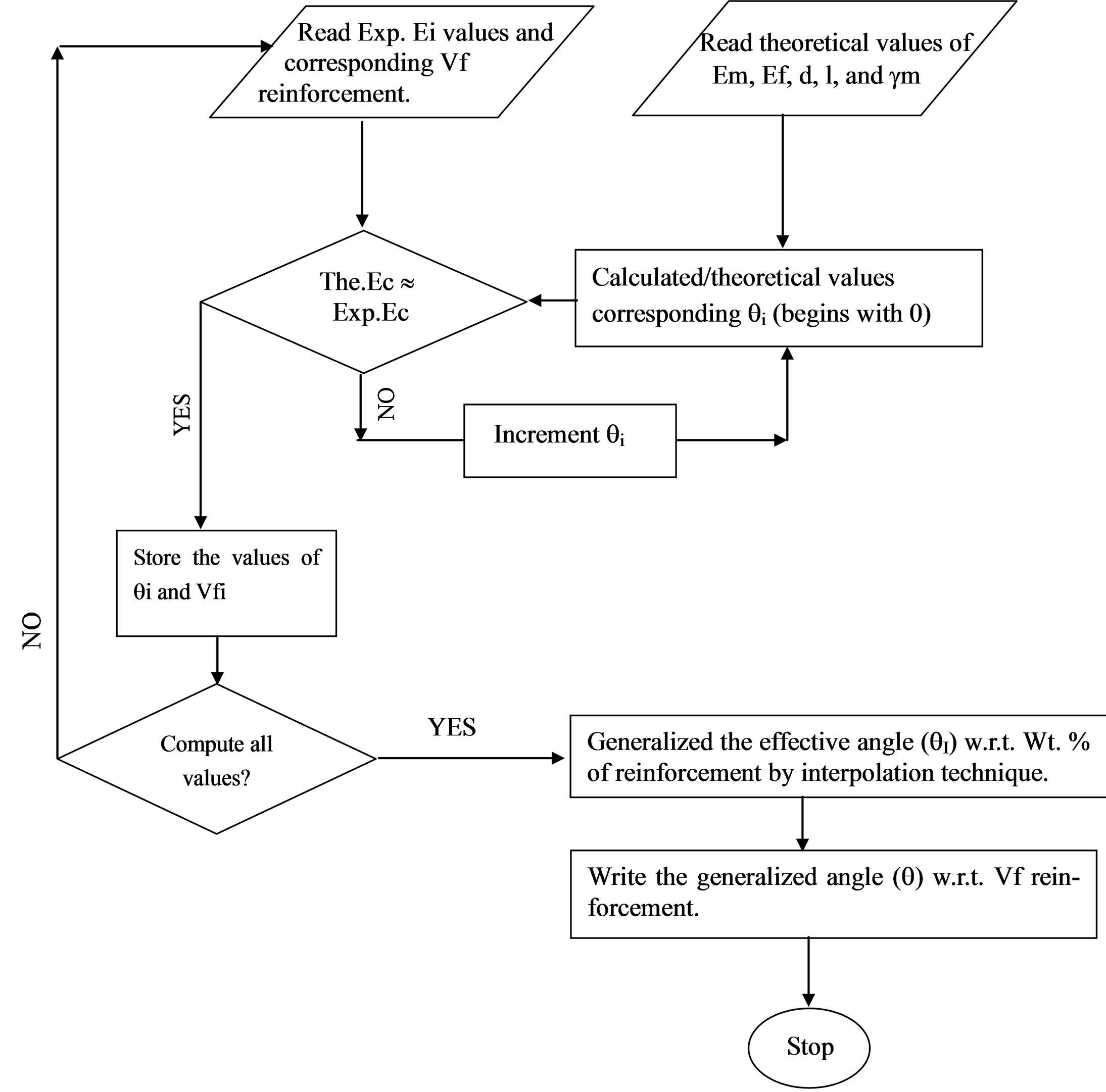
Figure 3. Flow chart for the computational of effective fiber angle (q).
properties of random fiber composites based on the approach originally introduced by Nielsen-Chen, in which,
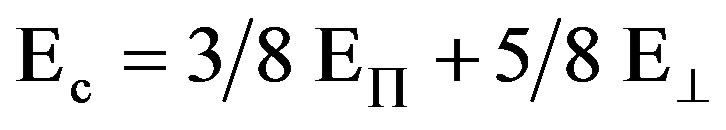 (7)
(7)
 (8)
(8)
And
 (9)
(9)
Another equation proposed by Nielsen-Chen takes into account the Poisson’s ratio and gives a better fitment to experimental results, viz.
 (10)
(10)
where
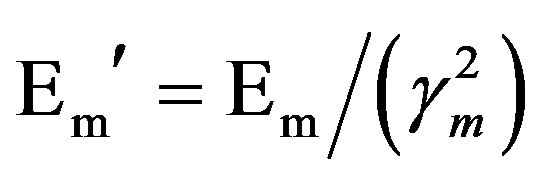 (11)
(11)
3.5. Strength
Nardone & Prwo [26] have proposed a computational shear-lag theory to describe the strengthening of the composites. They have postulated that the redistribution of matrix stress to the reinforcement through interfacial shear load transfer is the main contributing factor which results in the significant increase in yield strength. The theoretical UTS of the composite is expressed as (computational shear-lag model) [27]
 (12)
(12)
where syc & sym are the respectively the yield stresses of the composite and the matrix.
In the Miwa-model [28,29] the tensile strength sc of a composite, in which the short fibers are arranged in a random planar orientation, depend strongly on the yield shear strength at the fiber-matrix interface and is written as
 (13)
(13)
where L is the fiber length, d is the fiber diameter; sf & sm are the tensile strengths of the fiber and matrix respectively. Vf and Vm are weight of fiber and matrix respectively, sr is the thermal stress produced during molding of composite by the difference in the thermal expansion co-efficient between fiber and matrix material and is given by the following equation.
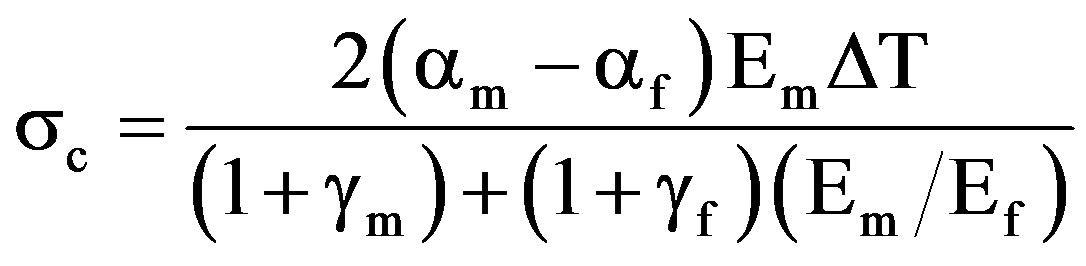 (14)
(14)
where a is the coefficient thermal expansion, E is the Young’s modulus, g is the Poisson’s ratio, DT is the difference temperature from the melting temperature of the matrix alloy to the room temperature. Suffixes m and f are the matrix and reinforcement fiber respectively.
4. Experimental Results
4.1. Elastic Modulus
The basalt short fiber may be regarded as acting efficiently if it carries a relatively high proportion of the externally applied load. This results in higher strength, as well as greater stiffness, because the basalt short fiber is usually stronger, as well as stiffer, than that of a matrix. The measured mean values of elastic moduli were plotted as a function of volume percentage of basal short fiber as shown in the Figure 4. McDanels [30] is of the opinion that the elastic modulus increases with increase in reinforcement content. However, elastic modulus has been found to be independent of the type of reinforcement. As short basalt short fiber content was increased from 2.5 to 10% by wt., an improvement in Young’s modulus of 13.26% has been observed. The sharp increase in Young’s modulus has been observed, and is probably due to the homogenous distribution of basal short fiber and the alignment of these basalt short fiber parallel to the axis with minimum segregation in the alloys. The Young’s modulus of the MMCs increased at lower rates when the weight % of the basalt short fiber of the MMCs is in range of 2.5 to 10.
The experimental results were compared with the theoretical data obtained from the shear-lag, computational model, and Nielsen-Chen model. Figure 4 shows plots of the Young’s modulus comparing the experimental data with the theoretical data obtained from shear-lag and Nielsen-Chen model for the reinforced composites with

Figure 4. Comparison of experimental and theoretical values of Young’s for Al/short basalt fiber composites.
2.5, 5, 7.5 and 10 short basalt short fibers in weight % respectively. The Nielsen-Chen model is in better agreement with the experimental value when compared with the shear-lag model, shear-lag model is well suited at lower volume fractions but in higher volume fraction, it over estimates the Young’s modulus. The shear-lag model assumes that fibers are aligned in the loading direction. Such alignment of short fibers in composites is not possible to produce by present casting techniques. Therefore the author has considered the effective angle of the aligned fiber in the composite adopting Shear-lag model to develop the computational model using the computer software in C++, which compares with the experimental data shown.
4.2. Tensile Properties
At the room temperature, only low to moderate increase in strength is observed in short fiber reinforced composites as the fibers are not oriented unidirectionally [31]. The tensile properties of the AL/short Basalt short fiber composite at laboratory temperature are summarized in graphs (the results reported are the mean values). The standard deviations were obtained from four experiment trials. Figure 5 shows the effect of short basal short fiber on UTS in Al MMCs. It can be seen that as the basalt short fiber content is increased, the UTS of the alloy material also increase. There is a marked increase in the UTS of the alloy from 15.5% to 28.7% as the basalt short fiber content is increased from 2.5 to 10 wt.%. The increase in UTS is attributed to the presence of hard basalt short fiber, which imparts strength to the matrix alloy, thereby providing enhanced tensile strength. Vogelsangs’ et al. [32] believes that the improvement in UTS may be due to the matrix strengthening. The reasons assigned are reduction in the alloy grain size and generation of a high dislocation density in the matrix, which is a result of the difference in thermal expansion between the metal matrix and the basalt short fiber reinforcement. The experimental results were compared with the theoretical data obtained from the computational shear-lag model and Miwa’s model. Figure 5 shows comparison between the experimental data and the theoretical data. All experimental values of the composite are in better agreement with the values predicated by the Miwa’s model than computational shear-lag model. In shear-lag model it has been assumed the fiber has aligned in the loading direction but all fibers were not aligned in the loading direction. Miwa has developed a model for random fiber distribution with differences in the coefficient of thermal expansion of the matrix material and reinforcements, and it is believed that the tensile strength depends strongly on the yield shear strength at the fibers-matrix interface.
4.3. Ductility
Figure 6 shows the effect of the basalt short fiber content

Figure 5. Comparison of the experimental and the theoretical UTS values.

Figure 6. Experimental values of % ductility.
on the ductility (% of elongation) of the MMCs. It can be seen from the graph that the ductility of the alloy decreases with the increase in basalt short fiber content from 2.5 to 10 wt.% (the ductility decrease by about 35.9%). This decrease in ductility in the MMCs is the commonly encountered disadvantage in MMCs when compared with the base alloys. Mummery et al. [33] is of the opinion that this behaviour is probably due to the voids, which nucleate during the plastic strains of the reinforcement or by reinforcement interface.
4.4. Optical and Scanning Electron Microstructure Analysis
The general features of the microstructure, e.g. fiber distribution, volume fraction, and orientation, were studied using an optical microscope and fractured surfaces were studied using a scanning electron microscope. Typical fractured surfaces of Al/basalt short fiber composite, obtained from tensile tests, are shown Figure 7(a). Typical fractographs of the tensile specimen unreinforced Al alloy that shows uneven distribution of the large dimples are shown in Figure 8. According to Withers [34], the experimental observation also suggests that short fibers rarely fracture. Only very few fibers can be seen as fractured and there is also an evidence of ductile failure in the matrix. The failure is few fibers split longitudinally and transversally as shown in the Figure 7(b). The failure of fibers in the composite may be attributed to the increase in stress on the specimen. As the load on the fiber increases, it induces strain in the fibers, and the most heavily loaded fiber fractures [35]. Some fiber “pull-out” has occurs in the samples, but the failure ap-
 (a)
(a) (b)
(b)
Figure 7. Fractrographs of the tensile specimen shows (a) fractured short Basalt fibers and (b) fiber puIlout from the specimen.

Figure 8. Fractographs of the tensile specimen unreinforced shows uneven distribution of the large dimples.
pears to be at the matrix end and not at the interfacial regions, as indicated by the conical cavities with rippled surface. Apparently more “pull-out” occurred in the matrix composite as expected due to the lower strength of the matrix. In some places where the fiber end was exposed to SEM, it appears that the matrix sheared away from the fiber [36].
5. Conclusions
A physical model was successfully developed to examine the elastic behavior of short basalt fiber reinforced with aluminum matrix.
1) Homogeneous dispersions of short Basalt fibers could be obtained by adopting liquid infiltration techniques.
2) The Nielsen-Chen model, computational model, and Miwa model can provide effective tools for the parametric studies of elastic properties of short fiber reinforced composite materials.
3) Comparisons with experimental results show that the theoretical models can be used to predict the elastic properties of the composite material.
4) The Young’s modulus and UTS of the composite material increase with increase in fiber volume fraction.
5) The ductility of the MMC decreases gradually with increase in fiber volume fraction.
NOTES