1. Perturbing Gravitational Potential P( )
)
We will set an inertial frame with the origin in the barycentre of the Sun-Mercury system, and not in the barycentre of the solar system; this is because we are going to examine Mercury’s orbit as a geodesic free-fall path, isolated from other planets gravitational interference.
Potential 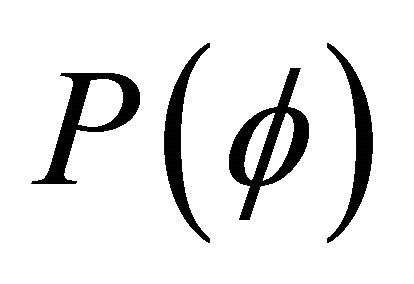 is defined as a slight perturbation to the Newtonian gravitational potential, linked with the radial velocity of the target. We also assume potential’s transmission velocity, equal to that of light (c).
is defined as a slight perturbation to the Newtonian gravitational potential, linked with the radial velocity of the target. We also assume potential’s transmission velocity, equal to that of light (c).
Consider a target with a radial speed Vr related to the inertial frame, moving in the same forward direction as the potential. The transit time of the potential crossing through the target, will be larger related with the transit time when the object is in a rest position and will decrease, if they are moving in opposite directions. The larger or reduced transit time between target and potential, is proportional to (Vr/c).
Be t1 the transit time of a potential crossing through an object. If the target moves in the same forward direction as the potential, the transit time t2 will be larger than t1 and will have the following expression, only acceptable if 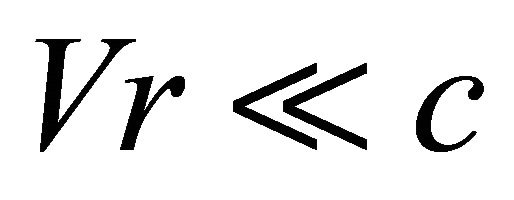 (leaving aside second order terms in magnitude, as radial acceleration):
(leaving aside second order terms in magnitude, as radial acceleration):
 (1)
(1)
 (2)
(2)
This coefficient , is the dimensionless ratio of the new real disturbing time (t2 – t1) related to the unperturbed transit time (t1).
, is the dimensionless ratio of the new real disturbing time (t2 – t1) related to the unperturbed transit time (t1).
The new gravitational potential is equal to the Newtonian, added with a perturbing action proportional to . Since the potential is an energy field with work characteristics, the perturbance is proportional to the square of time as it is the product of the acceleration by distance. The disturbance is not linear with time nor with the radial distance. It is also necessary to accept that as quantum electrodynamic iteration, the intensity is proportional to
. Since the potential is an energy field with work characteristics, the perturbance is proportional to the square of time as it is the product of the acceleration by distance. The disturbance is not linear with time nor with the radial distance. It is also necessary to accept that as quantum electrodynamic iteration, the intensity is proportional to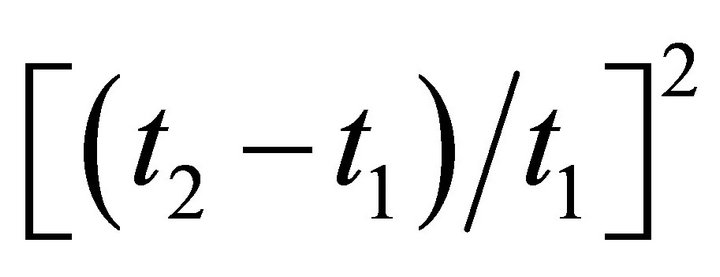 .
.
The motion of particles in an external gravitational field with a Maxwell framework, is in first order equivalent to a dynamic system linked with (v/c)2. [1]
Perturbing potential is then defined as:
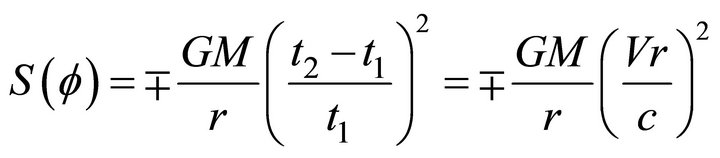 (3)
(3)
where  = true anomaly.
= true anomaly.  (same sign as gravity) for
(same sign as gravity) for  and
and  for
for .
.
As the Newtonian field, potential 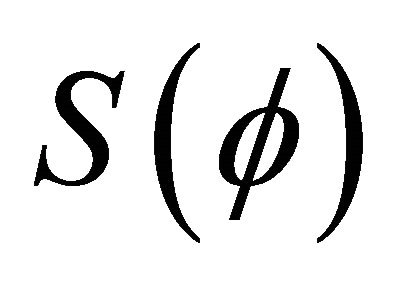 has a clear physical basis, consistent with the laws of impulse and momentum transfer, energy conservation and the action/ reaction effect of the usual mechanics. There is not therefore a new potential but the same classic gravitational field, perturbed by an action that increases/decreases slightly the force of gravity: the target has a radial speed.
has a clear physical basis, consistent with the laws of impulse and momentum transfer, energy conservation and the action/ reaction effect of the usual mechanics. There is not therefore a new potential but the same classic gravitational field, perturbed by an action that increases/decreases slightly the force of gravity: the target has a radial speed.
Final gravitational potential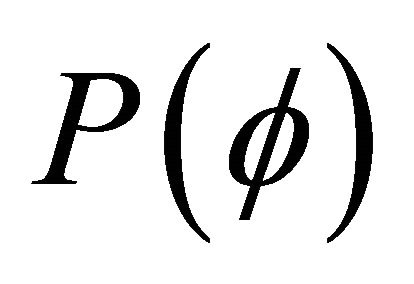 , will be the classic field, added with the perturbing potential.
, will be the classic field, added with the perturbing potential.
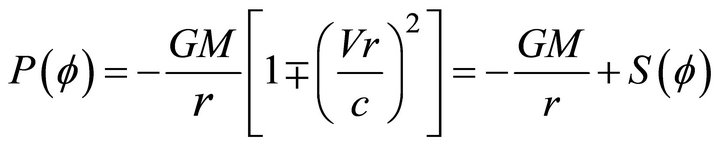 (4)
(4)
Point out that, if we apply potential 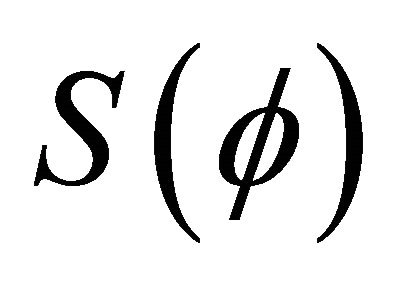 to any perfect sphere or any compact three-dimension target (instead of a single particle), the resultant ratio is three times (Vr/c)2 as we will conclude in Paragraph 5.
to any perfect sphere or any compact three-dimension target (instead of a single particle), the resultant ratio is three times (Vr/c)2 as we will conclude in Paragraph 5.
2. Equations of Motion of Mercury Induced by Potential 
Any small perturbing potential applied to a target in a keplerian ellipse, produces slight changes to the orbital parameters, first of all a precession, besides other minor actions such as the increase/decrease of the orbital axis and eccentricity.
Consider  as the instantaneous angular precession at each single point of the Newtonian ellipse. Precession will reach a final value (Δ) at the end of one orbit as result of its gradual accumulation. We will use Landau & Lifshitz formulation [2], which defines the precession produced by a perturbing potential. This formula is valid as a theorem, suitable for any small perturbation whatever could be its physical origin and returning the exact value. Integration is performed over an unperturbed orbit [3] (Using Langrange Planetary Equations, we reach a very similar result).
as the instantaneous angular precession at each single point of the Newtonian ellipse. Precession will reach a final value (Δ) at the end of one orbit as result of its gradual accumulation. We will use Landau & Lifshitz formulation [2], which defines the precession produced by a perturbing potential. This formula is valid as a theorem, suitable for any small perturbation whatever could be its physical origin and returning the exact value. Integration is performed over an unperturbed orbit [3] (Using Langrange Planetary Equations, we reach a very similar result).
 (5)
(5)
where M = m h = angular momentumδU = perturbing potential Energy =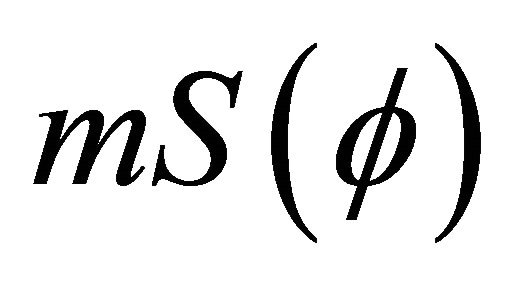 .
.
Then, the instantaneous precession referred to  is:
is:
 (6)
(6)
where h = angular momentum per unit of mass.
Applied to any elliptic orbit and a planet like Mercury:
 (7)
(7)
where e = eccentricity ; p = semi-latus

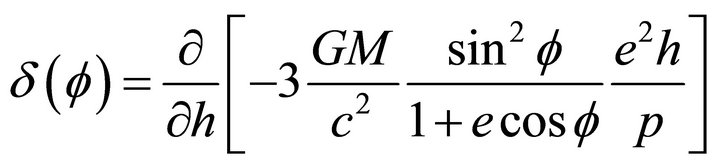 (8)
(8)
derivates referred to h are:
 [4]; (9)
[4]; (9)
and then:
 (10a)
(10a)

 (10b)
(10b)
 (11)
(11)
Final orbital precession Δ(2π), has the same value what ever could be the eccentricity (e > 0), and is exactly the final one orbit precession of:
 (12)
(12)
The resultant one orbit precession produced by perturbing potential  applied to Mercury and any elliptic orbit, is just exactly the same precession obtained by General Relativity in 1.915, which explained the anomaly discovered by LeVerrier in 1.859.
applied to Mercury and any elliptic orbit, is just exactly the same precession obtained by General Relativity in 1.915, which explained the anomaly discovered by LeVerrier in 1.859.
The question now, is how such action is achieved throughout the 88-days orbital period and what are the theoretical assumptions about the sequential and gradual progression of precession along the orbit. Potential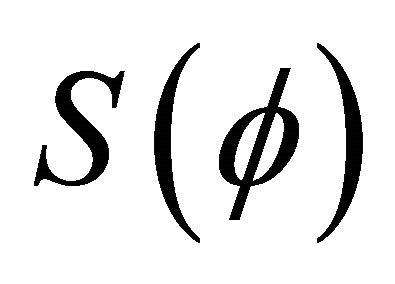 , and GR produce exactly the same final one orbit precession, however the equations of motion are not the same therefore, the instantaneous precession at each single point of the elliptic orbit is different. The instantaneous precession produced by
, and GR produce exactly the same final one orbit precession, however the equations of motion are not the same therefore, the instantaneous precession at each single point of the elliptic orbit is different. The instantaneous precession produced by , is not constant nor linear, causing an angular lead/lag (Ω) related to the fixed and linear GR precession.
, is not constant nor linear, causing an angular lead/lag (Ω) related to the fixed and linear GR precession.
Along the upward branch of the orbit, as Mercury moves away from the Sun, the radial velocity has the same forward direction as the gravitational potential, so perturbing acceleration increases gravity. Perturbing acceleration is directed inward the orbit, so Mercury will move inward in relation with the position it should occupy in the keplerian ellipse.
That means that the equilibrium position is located in a point nearer to the Sun: a “previous” point of the canonical trajectory. That is why the orbit, as a whole unperturbed ellipse, must then rotate a forward angle: a positive instantaneous precession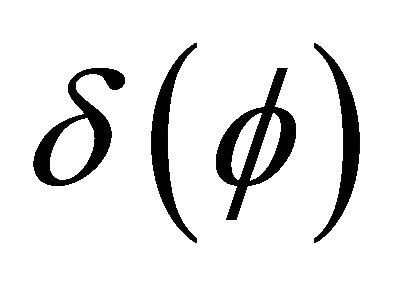 , whose amount is determined by Landau & Lifshitz formulation (Equations (10) and (11)).
, whose amount is determined by Landau & Lifshitz formulation (Equations (10) and (11)).
Along the descending branch of the orbit, Mercury comes closer to the Sun with a radial speed opposite to the gravitational potential, therefore perturbing acceleration, decreases gravity. The perturbing acceleration is directed outside the orbit, so Mercury will move outward in relation with the position it should occupy in the keplerian ellipse; the equilibrium position is located in a farther point to the Sun: a “previous” point of the canonical ellipse. The orbit must rotate also a forward angle: a positive instantaneous precession.
As seen in Figure 1, (graphic expression of Equations 10 and 11), the instantaneous precession 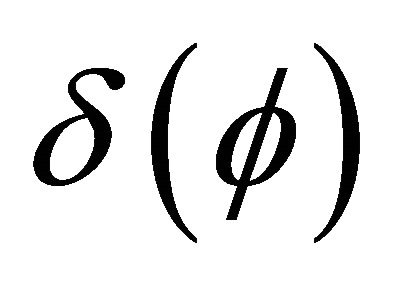 produced by potential
produced by potential , is always positive, producing a forward advance in both branches of the orbit. This is because perturbing potential produces a stable position which is always located in a “previous” point in the keplerian trajectory (Figure 2), and therefore precession is always positive and also with symmetrical magnitude about the major axis.
, is always positive, producing a forward advance in both branches of the orbit. This is because perturbing potential produces a stable position which is always located in a “previous” point in the keplerian trajectory (Figure 2), and therefore precession is always positive and also with symmetrical magnitude about the major axis.
In nearly all General Relativity textbooks and articles, the trajectory is defined starting from the Schwarzschild solution, in a geometry and a space-time with spherical symmetry. On that basis, the equation of the trajectory of Mercury, and any other elliptic orbit is:
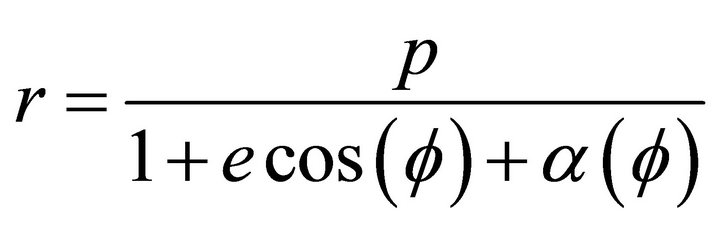 (13)
(13)
where 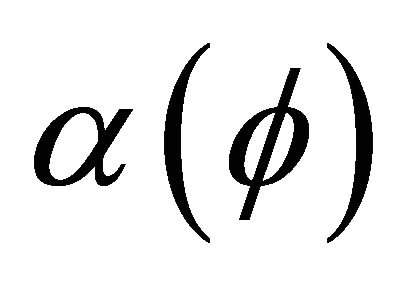 is a small function that produces the GR orbit differences, from the Newtonian kepler-ellipse: an orbit precession. The classic relativity textbook “Gravitation” by W. Misner [5], concludes in a linear progresssion:
is a small function that produces the GR orbit differences, from the Newtonian kepler-ellipse: an orbit precession. The classic relativity textbook “Gravitation” by W. Misner [5], concludes in a linear progresssion:
 (14)
(14)
with  = 2πK As result of it, GR instantaneous precession is steady, with a fixed ratio related to
= 2πK As result of it, GR instantaneous precession is steady, with a fixed ratio related to , so that the advance along one orbit, has a linear accumulation till its final value (Figure 1). This particular solution with a constant angular precession was, the first result obtained by Einstein in 1915 [6]:
, so that the advance along one orbit, has a linear accumulation till its final value (Figure 1). This particular solution with a constant angular precession was, the first result obtained by Einstein in 1915 [6]:
“...That contribution from the radius vector and described angle between the perihelion and the aphelion is obtained from the elliptical integral:
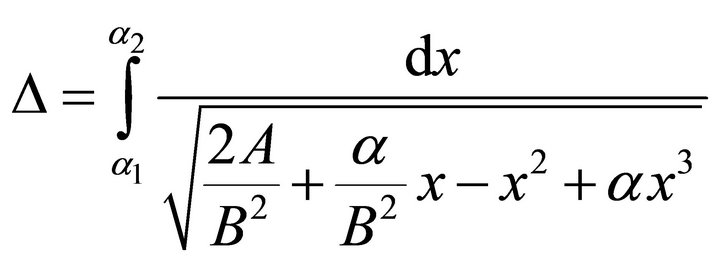 (15)
(15)
where α1 and α2 (…reciprocal values of the maximal and minimal distance from the Sun…)
GR admits also small periodic oscillations that are

Figure 1. Instantaneous (δ) and orbital (Δ) precession produced by GR and .
.


Figure 2. Instantaneous precession dynamics. Keplerian and perturbed orbit. Vr = radial velocity. anw = Newtonian acceleration. ap = perturbing acceleration. P1 = Position in the Keplerian ellipse. P2 = Position induced by perturbing acceleration. P3 = Equivalent position of P2 in the Keplerian ellipse.  = True anomaly. δ = Instantaneous Precession.
= True anomaly. δ = Instantaneous Precession.
insignificant contributions and their only effect is to change slightly the position of the perihelion and the interpretation of rmin and e [7].
The most extended and accepted formulation of GR orbit fluctuations is: [8]
 (16)
(16)
 also produces very small oscillations but in magnitude, are 1/30 related with those produced by
also produces very small oscillations but in magnitude, are 1/30 related with those produced by  potential. There are also other proposals based in a particular solution of the Schwarzschild’s methodo-logical approaches [9].
potential. There are also other proposals based in a particular solution of the Schwarzschild’s methodo-logical approaches [9].
The peak instantaneous precession produced by  is at
is at  = 1.73 rad,
= 1.73 rad,  = 4.56 rad, very close to the peak values of Vr (Figure 2). The maximum angular lead/lag is at
= 4.56 rad, very close to the peak values of Vr (Figure 2). The maximum angular lead/lag is at  = 5.42 rad and
= 5.42 rad and  = 0.85 rad, with Ω = ±K ´ 0.54 rad related to the fixed and linear GR precession.
= 0.85 rad, with Ω = ±K ´ 0.54 rad related to the fixed and linear GR precession.
The peak positional lead/lag of Mercury, would happen in A [ = 2.46 rad] and B [
= 2.46 rad] and B [ = 3.82 rad]. This is because in these points, the radius is larger.
= 3.82 rad]. This is because in these points, the radius is larger.
In case A, Mercury would be in a forward position regarding a GR precession. This relative position would be i = 2.4 ´ 103 m (transversal vector) and j = –0.36 ´ 103 m (radial vector), magnitudes which would be equal but with opposite sign in B. Also point out that in about 21 days, Mercury would move from the peak forward position (A) to the most delayed (B), always referred to the relative location with a constant GR precession.
Spacecraft Messenger has begun to orbit Mercury past March 18 (2011), and during two years, both will make 8.4 revolutions around the Sun. That event should afterwards allow to measure and draw accurately the geometry of the whole orbit of Mercury, as an open geodesic free-fall path, isolated from other planets gravitational interference. Another alternative is to wait till the BepiColombo be launched in 2015, an European mission to Mercury where, testing relativistic gravity is recognized as a crucial scientific objective.
3. The Increase of Eccentricity of the Orbit of the Moon
This increase has recently been presented [10], collecting the data extracted by the Lunar Laser Ranging along 39 years since its deployment in the Moon by the Apollo missions.
The increase is: (9 ± 3) ´ 10−12/year [11,12].
We will analyse the effects of a small perturbing acceleration over the eccentricity of any elliptic orbit. According to Gauss Planetary Equations, (only acceptable when  and low orbit inclination), the eccentricity variation, is linked with the perturbing acceleration, whatever could be its physical origin:
and low orbit inclination), the eccentricity variation, is linked with the perturbing acceleration, whatever could be its physical origin:
 (17)
(17)
where Ar is the radial perturbing acceleration.
The perturbing acceleration is the derivative of the perturbing potential 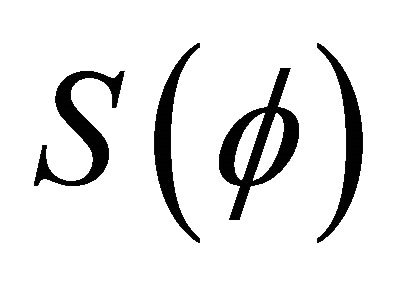 related to r, the same as we do to obtain the Newtonian acceleration from the classic gravitational field. All the particles of the target have the same perturbing acceleration whatever they are located in the body:
related to r, the same as we do to obtain the Newtonian acceleration from the classic gravitational field. All the particles of the target have the same perturbing acceleration whatever they are located in the body:
 (18)
(18)
 (19)
(19)
where Ar > 0 (same sign as gravity) for  and Ar < 0 for
and Ar < 0 for .
.
If we develop Equation (17) and change derivatives related to time (t) with that related to 
 (20)
(20)
For a Keplerian ellipse, we have also:
 (21)
(21)
and then,
 (22)
(22)
The integration will give the eccentricity increase along one orbit of the Moon around the Earth. Potential  always produces a positive and symmetrical effect about the axis of the ellipse. If we consider the sign of Ar in each branch of the orbit, we can integrate between 0 and π with a double factor.
always produces a positive and symmetrical effect about the axis of the ellipse. If we consider the sign of Ar in each branch of the orbit, we can integrate between 0 and π with a double factor.
 (23)
(23)
the definite integral is:
 (24)
(24)
The Earth/Moon parameters are: GM = 3.986 ´ 1014 m3×s–2; e = 0.0549; a = 3.84 ´ 108 m The increase of eccentricity in one orbit is:
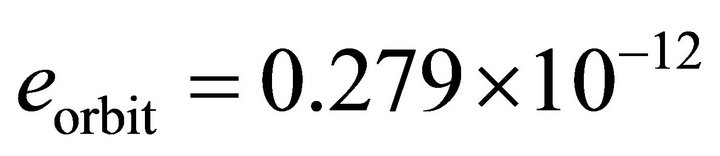 (25)
(25)
and referred to a year:
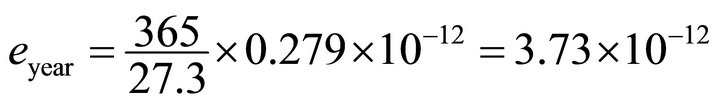 (26)
(26)
Then, we can conclude that the increase of eccentricity of the orbit of the Moon produced by potential , is consistent with the data obtained by astronomical detection through the Lunar Laser Ranging.
, is consistent with the data obtained by astronomical detection through the Lunar Laser Ranging.
4. The Increase of the Astronomical Unit
The increase of the Astronomical Unit was analysed by Krasinsky [13] however, there is not a clear explanation of its origin.
The increase is: 15 ± 4 cm/year.
Perturbing potential  produces an increase in the semi-major axis of the ellipse that, according to Gauss Planetary Equations, will have the following expression:
produces an increase in the semi-major axis of the ellipse that, according to Gauss Planetary Equations, will have the following expression:
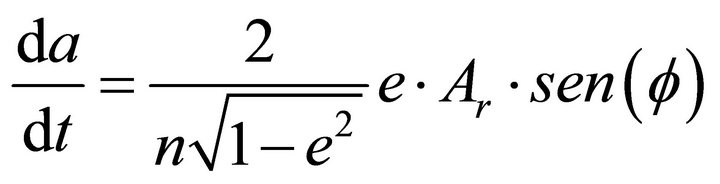 (27)
(27)
Using similar formulations as in paragraph before,
 (28)
(28)
For one orbit of the Earth around the Sun,
 (29)
(29)
 (30)
(30)
The Earth-Sun parameters are:
GM = 13.27 ´ 1019 m3×s–2; e = 0.0167 and then:
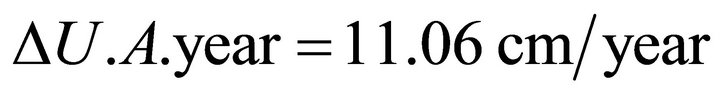 (31)
(31)
Then, we can conclude that the increase of the Astronomical Unit produced by potential  applied to the orbit of the Earth, is consistent with the data obtained by astronomical detection through the analysis of radiometric measurements of distances between the Earth and the major planets including observations from Martian orbiters from 1.971.
applied to the orbit of the Earth, is consistent with the data obtained by astronomical detection through the analysis of radiometric measurements of distances between the Earth and the major planets including observations from Martian orbiters from 1.971.
If we apply Gauss equations to the orbit of other planets, these would be only acceptable for those with a very low eccentricity. In other cases with higher eccentricity orbits, (as Mercury), the Gauss planetary equations and others related [14], are not appropriate, applied to  perturbing potential. The results are:
perturbing potential. The results are:
 ;
; ;
;

5. Potential  Application to a Three Dimension Solid Sphere
Application to a Three Dimension Solid Sphere
 is a perturbation of the classic gravitational potential due to the higher/lower pulse of time that implies a radial velocity of the target. The coefficient (Vr/c)2, is a dimensionless ratio which defines the relation between the applied potential to one particle that moves with a radial velocity related with another with a perfect circular orbit. Instead of a particle, we will consider a solid sphere and the perturbing potential
is a perturbation of the classic gravitational potential due to the higher/lower pulse of time that implies a radial velocity of the target. The coefficient (Vr/c)2, is a dimensionless ratio which defines the relation between the applied potential to one particle that moves with a radial velocity related with another with a perfect circular orbit. Instead of a particle, we will consider a solid sphere and the perturbing potential  transit action (Figure 3). The trasmission coefficient is different.
transit action (Figure 3). The trasmission coefficient is different.
Be t1 the transit time of the potential through the equatorial diameter of the sphere, when the target is moving in a perfect circular orbit. When the target has a radial velocity Vr (elliptic orbit), the force of gravity associated with the potential, should produce and transmit during t1, a larger quantity of energy-work than before; the distance travelled has been enlarge with a new length of Vr ´ t1 producing a very small increase of the sphere’s active volume, linked with the perturbing action: A1 ´ Vr ´ t1 (Figure 3)
In order to distribute this new energy, balanced between all the particles of the target, we must consider:
a) Energy (E) transmitted is in direct proportion to the spherical surface (A1).
b) Not all the diameters have the maximum length as in the equator.
c) The coefficient only compares the perturbing action regarding the initial situation.
d) Distribution of the “perturbing action” volume, between the total volume of the sphere.
Therefore, the coefficient k will be:
 (32)
(32)
and then: 
6. Conclusions
Potential  is defined as a slight perturbation to the
is defined as a slight perturbation to the
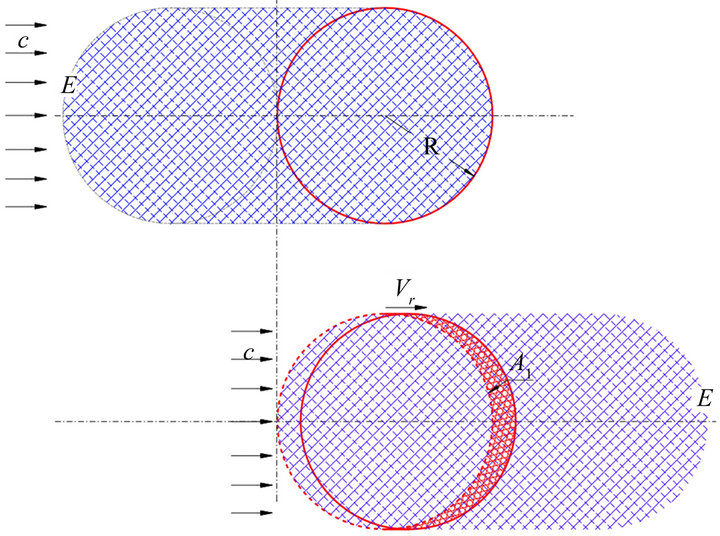
Figure 3. Perturbing potential action through a three dimension solid sphere with a radial velocity (Vr).
Newtonian gravitational potential, linked with the radial velocity of the target. The larger or reduced transit time between target and potential, is proportional to ±(Vr/c), coefficient that gives the relative increase or reduction ratio related with a particle-target in a rest position or a perfect circular movement. There is not therefore a new potential but the same classic field, perturbed by an action that increases/decreases slightly the force of gravity: the target has a radial speed.
Applied to the orbit of Mercury, produces exactly the same one orbit secular precession deduced by General Relativity; however, the equations of motion are not the same, and that means differences in the instantaneous angular precession. The instantaneous precession, could be detected by Messenger spacecraft which is now orbiting Mercury and the Sun. Another alternative is to wait till the BepiColombo be launched in 2015. These data should be reduced with the perturbations produced by other planets. It is certainly a difficult and complex duty but clearly available with the current development of our technology and also not expensive.
Close to reach the centenary of the formulation and first success of General Relativity, there are still some open issues.
We suggest in this paper, to update the classic test of General Relativity, studying the gradual progression of precession, not only in its perihelion, but also along a complete trajectory around the Sun.
 potential applied to the orbit of the Moon around the Earth, produces an increase of the eccentricity that is consistent with the real observed data.
potential applied to the orbit of the Moon around the Earth, produces an increase of the eccentricity that is consistent with the real observed data.
 potential applied to the orbit of the Earth, produces an increase of the Astronomical Unit which is consistent with the real observed data.
potential applied to the orbit of the Earth, produces an increase of the Astronomical Unit which is consistent with the real observed data.
Point out that it is really significant that the same gravitational potential with clear physical boundary conditions, consistent with the laws of impulse and momentum transfer, energy conservation and the action/reaction effect of the classical mechanics, could explain directly this three singularities, without any “ad hoc” parameters arrangement.
Does these theoretic proposals suit with the complete geodesic trajectory of Mercury?
7. Appendix
 potential produces a similar effect as the observed flat rotation curves of spiral galaxies. It would be appropriate to complete the studies related with spiral galaxies, but now, with these new
potential produces a similar effect as the observed flat rotation curves of spiral galaxies. It would be appropriate to complete the studies related with spiral galaxies, but now, with these new  potential proposals.
potential proposals.