Irrigation Planning with Conjunctive Use of Surface and Groundwater Using Fuzzy Resources ()
1. Introduction
In water management practices conjunctive use is considered important as surface and groundwater are related systems. Uncertainty in the parameters involved makes it difficult for the decision maker to derive the water use policy and estimate the returns from the system. Such uncertainties are efficiently tackled through fuzzy logic. Kashyap and Chandra [1] have developed a mathematical model for achieving an optimal conjunctive use policy incorporating spatially and temporally distributed groundwater withdrawals and spatially distributed cropping patterns. The groundwater withdrawals were constrained to keep the water table elevations within an appropriate range. Murthy [2] illustrated with a hypothetical example the case of conjunctive use of surface and groundwater to replace surface water. Onta et al. [3] have developed a stochastic dynamic programming model to derive the optimal operating policy and also a lumped simulation model is used to evaluate the alternative policies for each alternative and a multiple criteria decision making is used to select the most satisfactory alternative plan. Mohan and Jyothiprakash [4] have formulated a FLP model to derive optimal crop plans for an irrigation system for conjunctive use of surface and groundwater. The results of FLP model were compared with classical linear programming model which showed that the fuzzy linear programming model maximized the degree of satisfaction. Vedula et al. [5] have developed a mathematical model to obtain an optimal conjunctive use policy for irrigation with the objective of maximizing the sum of relative yields of crops in a reservoir-canal-aquifer system. The crop water allocations are achieved by integration of the reservoir operation for canal release along with groundwater pumping. Srinivasulu and Satyanarayana [6] addressed the problem of a canal irrigated in saline groundwater areas by developing a linear programming model for allocation of land and water resources to different crops. A genetic algorithm model was developed by Nagesh Kumar et al. [7] to obtain an optimal operating policy and optimal crop water allocations with the objective of maximizing the relative yields from the crops in the study area. Manuel et al. [8] have presented an integrated non linear hydrologic economic modeling framework for optimizing conjunctive use of surface and groundwater for a river basin through capacity expansion. Khare et al. [9] have presented an economic optimization problem to explore the potential use of surface and groundwater resources using linear programming to arrive an optimal cropping pattern for maximization of net benefits. Kentel and Aral [10] have developed a simulation-optimization model with constraints on drawdown that have been used to optimize the additional groundwater withdrawal in a coastal aquifer. The results were used to determine the individual satisfaction degrees with respect to multiple objectives. Yang et al. [11] have developed a multi objective problem by integrating the multi-objective genetic algorithm, constrained differential dynamic programming and groundwater simulation model. These models are adopted to distribute the optimal releases. Regulwar and Anand Raj [12] have developed a Multi Objective Genetic Algorithm Fuzzy Optimization model which is applied to a multireservoir system. A 3-D optimal surface was evolved for deriving the optimal operation policies of the reservoir. Regulwar and Kamodkar [13] have developed a FLP model to evaluate the reservoir operation policy in which the resources were fuzzy in the first model; in the second model, the technological coefficients were fuzzified and in the third model both i.e. the resources and the technological coefficients were considered fuzzy. Gurav and Regulwar [14] have formulated an irrigation planning problem as (FLP) to tackle the uncertainties to derive the optimal cropping pattern with an objective of minimization of cost cultivation applied to a case study. Kamodkar and Regulwar [15] have developed a reservoir operation model using FLP which considers two objective functions. Fuzziness was considered in the objectives and constraints to derive the reservoir operation policy in a water year.
From the literature, it is evident that conjunctive use policy has been used to evolve the surface and groundwater resources allocation optimally and applied to an irrigation planning problem. Different strategies based on the status of the resources available with different alternatives of surface and groundwater utilization have been used for the allocation of resources utilized in irrigation planning on a linear programming framework. Other techniques such as non linear programming, stochastic dynamic programming and simulation appear in the literature for obtaining the solution of such problems. Linear programming based optimization methods are popularly used to derive the policies and are found as an effective tool in dealing with such problems. However it is observed that in a crisp optimization problem there is no flexibility in the constraints especially the resources. To incorporate relaxation in the constraints and look at the acceptability of the solution, the crisp optimization problem can be converted into fuzzy optimization problem.
The objective of the present study is to formulate a linear programming model to maximize the net benefits and to arrive at an optimal cropping pattern in a fuzzy environment. The groundwater availability of the study area is explored on the basis of Vertical Electrical Soundings (VES). The Language for Interactive General Optimization (LINGO) has been used to solve the linear optimization problem.
2. Methodology
Uncertainty is inevitable in irrigation planning due to random nature of events and fluctuating inputs. In the present study the applicability of irrigation planning model is improved by incorporating the uncertainties in the resources and representing them as fuzzy sets instead of crisp value. A FLP model is presented which considers uncertainty in the resources where as the other parameters are crisp in nature. The degree of satisfaction (l) of a certain value of the resource within the fuzzy set is represented by membership function.
Model: The Fuzzy Linear Programming Problem with Fuzzy Resources
 (2.1)
(2.1)
In this case, 
 is a fuzzy numbers with the following linear membership function
is a fuzzy numbers with the following linear membership function
 (2.2)
(2.2)
Where  (Figure 1) for each vector
(Figure 1) for each vector
 we first calculate the degree,
we first calculate the degree,  to which
to which  satisfies the
satisfies the 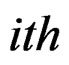 constraint
constraint  by the formula
by the formula

Figure 1. Linear membership function for resources .
.
 (2.3)
(2.3)
These degrees are fuzzy set on and their intersection
and their intersection  is a fuzzy feasible set. Next, we determine the fuzzy set of optimal values. This is done by calculating the lower and upper bounds of the optimal values first. The lower bound of optimal values
is a fuzzy feasible set. Next, we determine the fuzzy set of optimal values. This is done by calculating the lower and upper bounds of the optimal values first. The lower bound of optimal values  is obtained by solving the standard linear programming problem;
is obtained by solving the standard linear programming problem;
 (2.4)
(2.4)
The upper bound of the optimal values  is obtained by a similar linear programming problem in which each
is obtained by a similar linear programming problem in which each  is replaced with
is replaced with :
:
 (2.5)
(2.5)
Then the fuzzy set of optimal values,  which is fuzzy subset of
which is fuzzy subset of  is defined by a linear membership function
is defined by a linear membership function 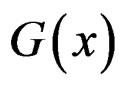 for objective as,
for objective as,
 (2.6)
(2.6)
Graphical representation of linear membership function given by Equation (2.6) for fuzzy goals is shown in Figure 2.

Figure 2. Linear membership function for goals.
The fuzzy set of the  constraint,
constraint,  which is subset of
which is subset of , is defined by
, is defined by
 (2.7)
(2.7)
Graphical representation of linear membership function given by Equation (2.7) for fuzzy resources is shown in Figure 1.
By incorporating the above information (the problem given by Equation (2.1) becomes the following optimization problem
 (2.8)
(2.8)
By using Equations (2.6) and (2.7), Equation (2.8) can be written as
 (2.9)
(2.9)
Where,  is the level of satisfaction. The above problem is actually a problem of finding
is the level of satisfaction. The above problem is actually a problem of finding  such that
such that
 (2.10)
(2.10)
reaches the maximum value. This is a problem of finding a point ( ) which satisfies the constraints and goal with the maximum degree. The method employed here is called as symmetric method (i.e. the constraints and the goal are treated symmetrically) [16].
) which satisfies the constraints and goal with the maximum degree. The method employed here is called as symmetric method (i.e. the constraints and the goal are treated symmetrically) [16].
3. Description of the Study Area
The Jayakwadi project is constructed across river Godavari which originates in the Nasik district of Maharashtra State, India. The project is a multipurpose project having a catchment area of 21,755 km2, Gross storage capacity of 2909 Mm3 and Live storage capacity of 2171 Mm3. A system of canals i.e Left bank canal and Right bank canal serves a command area of 141640 ha and 41682 ha respectively. The entire command area lies within the Latitude: 18˚46'N to 19˚30'N and Longitude 75˚20'E to 77˚45'E. Figure 3 shows the Index Map of Jayakwadi Project.
The cropping pattern of the command is determined on the considerations that there is a suitable combination of food crops and cash crops and minimizing delta to maximum possible extent consistent with the productivity of the project. The project is planned for 75% dependable yield and crops are grown throughout the year. The irrigation intensity adopted is 22% in kharif season, 45% in Rabi season, 28% in two seasonal, H.W. crop 3% and perennial 4.5% which gives a total irrigation intensity of 102%. A geoelectric field survey was carried out by applying the Vertical Electrical Sounding (VES) technique which measures the electrical resistivity variation with depth to locate the groundwater resources for irrigation in the canal command of Jayakwadi Project. The geoelectric field measurements are conducted using Computer Resistivity Monitor (CRM). The study was conducted at 10 locations of the area using Schlumberger configurations. Hence it is evident from the above studies that water is available between a depth of 9 - 12 m below ground level to a depth of 35 m and it is observed that this water level fluctuates to give a yield up to 69.56% based on the stage of groundwater development GEC 97 [17]. The monthly surface water availability cannot exceed the availability of water from the canal. The monthly optimal operating policy adopted for irrigation releases from the reservoir for a dependable yield of 75% based on the Preliminary Irrigation Program (PIP). The monthly irrigation requirement for all the crops is met by the releases from the reservoir and the water requirement is estimated by Modified Penman Method with an overall efficiency of 49% [18].
3.1. Model Formulation
3.1.1. Objective Function
The objective function consists of maximizing the benefits (Z) from the command area of Jayakwadi project. The net benefit is obtained by deducting the cost of production from the yield and income obtained from an individual crop on unit area basis and the cost of surface and groundwater.
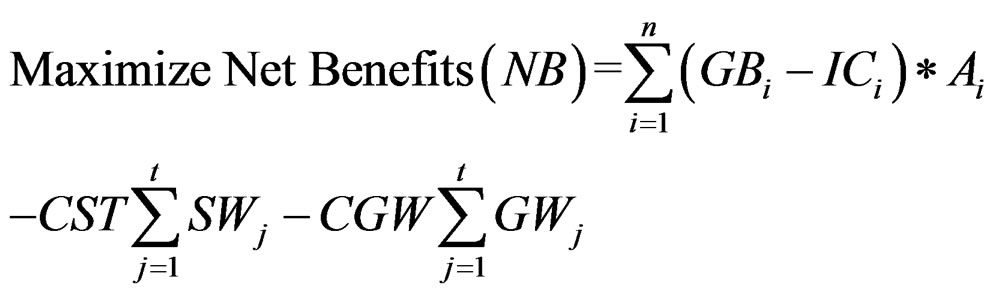 (3.1)
(3.1)
whereNB = Net benefit of ith crop in Million Rupees.
GBi = Gross Benefit of ith crop per ha.
ICi = Input Cost for ith crop per ha.
Ai = Area under ith crop (i = 1, 2, 3, ..., 10), 1 = Sugarcane, 2 = Banana, 3 = Chillies, 4 = L.S.Cotton, 5 = Kharif Jowar, 6 = Paddy( Drilled), 7 = Rabi Jowar, 8 = Wheat, 9 = Gram, 10 = Groundnut (H.W).
Where GB = (Yield × Income)-Cost of Production excluding the cost of surface and groundwater (The Report of Commissionerate of Agriculture Maharashtra State 2010, Agricultural Statistical Information Maharshtra State, India).
CST is the cost of surface water and is estimated to be 11760 Rs./ha for a Benefit Cost Ratio of 1.5 for Jayakwadi Project (Jayakwadi Project Report).
CGW is the cost of groundwater which is estimated to be Rs 30,000 Rs/ha including the capital cost and charges been claimed by the local authorities (Maharashtra Jeevan Pradhikaran).
SW = Surface water allocation in jth time period (1, 2, 3…12).
GW = Groundwater allocation in jth time period (1, 2, 3…12).
3.1.2. Constraints
(1) Water requirement constraint
 (3.2)
(3.2)
Where, WRi = Water requirement of ith crop in Mm3
(2) Area availability constraint The total area under each crop should not exceed the Culturable Command Area for all seasons
 (3.3)
(3.3)
CCAi = Culturable command area for ith crop in ha.
(3) Surface water availability constraint The monthly surface water availability cannot exceed the availability of water from the canal
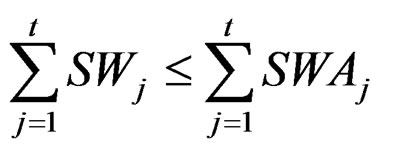 (3.4)
(3.4)
SWAj = Surface water available in jth time period (1, 2, 3… 12) in Mm3 based on the Preliminary Irrigation Program for a water year.

Figure 3. Index map of Jayakwadi project.
(4) Groundwater availability constraint The total water pumped annually from the groundwater resources of the study area should not exceed the annual recharge.
 (3.5)
(3.5)
GWAj = Groundwater available in jth time period (1, 2, 3…12) in Mm3.
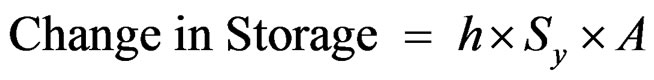
where h = Fluctuation in water level in m, Sy = Specific Yield (for consolidated formations Sy = 0.02) and A = Area for computation of recharge.
4. Results and Discussions
In the present study a FLP model is applied to a case study of Jayakwadi Project which is a multipurpose project serving a command area of 141640 ha (PLBC) and 41682 ha (PRBC). The objective of the present model is to maximize the net benefits subject to constraints of area, surface water and groundwater availability. The model considers uncertainty involved in the resources  i.e. area, surface water and groundwater availability. Whereas the other parameters of the model i.e. the technological coefficients
i.e. area, surface water and groundwater availability. Whereas the other parameters of the model i.e. the technological coefficients  and cost coefficient
and cost coefficient  are crisp in nature. By using the methodology as explained earlier (Equations 2.4 and 2.5) the lower bound and upper bound of the optimal values are estimated first by solving the standard linear programming problem. As the canal command faces frequent water scarcity, 100 % availability of the resources is taken into consideration as the upper bound for crop area, surface water and groundwater. The lower bound for area is restricted to 77%, for surface water it is considered to be 78% as per the (PIP) and 69.56% for groundwater availability based on stage development (GEC 97). The fuzzy set of optimal values is defined by a linear membership function (Equation (2.6)). The values of upper and lower bounds of the objective function are 2308 Million Rupees and 1620 Million Rupees respectively. By incorporating the above information in the problem given by Equation (2.1) becomes the fuzzy optimization problem (Equation 2.8). Using Equations (2.6), (2.7) and (2.8), the maximum value which satisfies the constraints and goal with a maximum degree of satisfaction
are crisp in nature. By using the methodology as explained earlier (Equations 2.4 and 2.5) the lower bound and upper bound of the optimal values are estimated first by solving the standard linear programming problem. As the canal command faces frequent water scarcity, 100 % availability of the resources is taken into consideration as the upper bound for crop area, surface water and groundwater. The lower bound for area is restricted to 77%, for surface water it is considered to be 78% as per the (PIP) and 69.56% for groundwater availability based on stage development (GEC 97). The fuzzy set of optimal values is defined by a linear membership function (Equation (2.6)). The values of upper and lower bounds of the objective function are 2308 Million Rupees and 1620 Million Rupees respectively. By incorporating the above information in the problem given by Equation (2.1) becomes the fuzzy optimization problem (Equation 2.8). Using Equations (2.6), (2.7) and (2.8), the maximum value which satisfies the constraints and goal with a maximum degree of satisfaction  is achieved. Results for maximized Lamda
is achieved. Results for maximized Lamda  for fuzzy resources are given in Table 1. It is observed that while solving the linear programming problem for upper bound and lower bound of the resources the area allocated for groundnut is the same but it shows a considerable increase in the area in the optimal cropping pattern. The irrigation intensities for upper bound, lower bound and for fuzzy optimization problem are observed to be 84.78%, 61.18% and 77.38% respectively from which it is evident that optimization of resources in a fuzzy environment gives results with a satisfaction level up to 0.546 taking care of the vagueness and uncertainties in the availability of resources. From the solution it is observed that a maximized benefit of 1994 Million Rupees is obtained for an irrigation intensity of 77.38%. Figure 4 shows the graphical representation of the optimal cropping pattern.
for fuzzy resources are given in Table 1. It is observed that while solving the linear programming problem for upper bound and lower bound of the resources the area allocated for groundnut is the same but it shows a considerable increase in the area in the optimal cropping pattern. The irrigation intensities for upper bound, lower bound and for fuzzy optimization problem are observed to be 84.78%, 61.18% and 77.38% respectively from which it is evident that optimization of resources in a fuzzy environment gives results with a satisfaction level up to 0.546 taking care of the vagueness and uncertainties in the availability of resources. From the solution it is observed that a maximized benefit of 1994 Million Rupees is obtained for an irrigation intensity of 77.38%. Figure 4 shows the graphical representation of the optimal cropping pattern.
5. Conclusions
The modeling procedure demonstrates the vagueness and uncertainties in the availability of resources which are tackled to evolve an optimal cropping plan. FLP model is formulated for maximization of net benefits applied to a case study of Jayakwadi Project. Following conclusions are drawn.
1) Uncertainty in the availability of resources makes it difficult for the decision maker to derive the water use

Table 1. Optimal cropping pattern for upper bound, lower bound and maximized lamda (λ).

Figure 4. Optimal cropping pattern for upper bound, lower bound and fuzzy resources.
policy and estimate the returns from the system. Such uncertainties are efficiently tackled through fuzzy logic.
2) The irrigation intensities for upper bound, lower bound and for fuzzy optimization problem are observed to be 84.78%, 61.18% and 77.38%, respectively.
3) Optimization of resources in a fuzzy environment gives results with a satisfaction level up to 0.546 taking care of the vagueness and uncertainties in the availability of resources.
4) It is observed from the solution that the maximized benefit of 1994 Million Rupees is obtained for an irrigation intensity of 77.38%.
6. Acknowledgements
The authors are thankful to Command Area Development Authority, Aurangabad, Maharashtra State, India for providing necessary data for the analysis and Head, Geology Department, Government Institute of Science Aurangabad, for their support to carry out the field observations.