A Note on Generalized Inverses of Distribution Function and Quantile Transformation ()
1. Introduction
A distribution function defined on  is a map
is a map 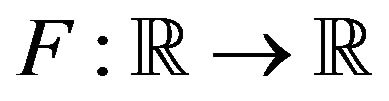 such that F is nondecreasing and right continuous (see for example [1], p. 22). It is called a probability distribution function (PDF) if
such that F is nondecreasing and right continuous (see for example [1], p. 22). It is called a probability distribution function (PDF) if
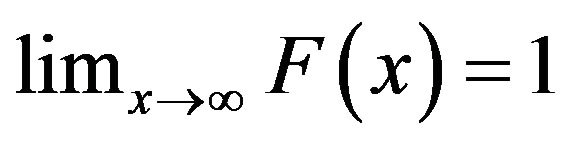 and
and . Suppose X is a random variable with distribution function F which is continuous, then
. Suppose X is a random variable with distribution function F which is continuous, then  has standard uniform distribution. Furthermore, if F is also strictly increasing with inverse
has standard uniform distribution. Furthermore, if F is also strictly increasing with inverse , and U is a standard uniform random variable, then
, and U is a standard uniform random variable, then  has distribution function F. This fact is the basis for generating random numbers given a distribution function. Hence if F is a PDF,
has distribution function F. This fact is the basis for generating random numbers given a distribution function. Hence if F is a PDF,  is also called the quantile function of F [2].
is also called the quantile function of F [2].
The distribution function dose not, in general, have an inverse (in strict sense) as it may be not strictly increasing, for example, the PDF of a discrete random variable. In statistics, the empirical distribution function (EDF) from a random sample is a step function. If we want to (nonparametrically) estimate the population quantiles from the sample data, we need to find an appropriate ‘inverse’ of the EDF. Unfortunately there is no universally accepted definition of sample quantiles given the data. For example, Langford [3] compares many methods proposed in literatures to calculate quantiles from data and finds that none of them is uniformly better than others.
There are four meaningful ways to define a generalized inverse of a distribution function F as follows:

It’s easy to see that these methods are different in dealing with endpoints of flat parts if F is not strictly increasing. In fact,  is the definition of generalized inverse in literatures, for example, [4-7]. It’s obvious that all these generalized inverse functions are nondecreasing and equal the inverse of F if F is strictly monotone increasing.
is the definition of generalized inverse in literatures, for example, [4-7]. It’s obvious that all these generalized inverse functions are nondecreasing and equal the inverse of F if F is strictly monotone increasing.
In this manuscript we study some properties of these four functions and their relations to the quantile transformation in probability theory. The quantile transformation is the theoretical basis for random number generation in simulation studies in statistics. In simulation studies we usually need to generate random samples from a given distribution. The general method is first to generate uniform random variables on 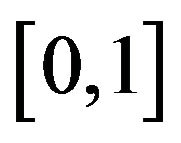 and then to use the quantile transformation to transform the uniform random variables to the random sample we need. Our results shows that any one of the generalized inverses defined above will work as the quantile transformation.
and then to use the quantile transformation to transform the uniform random variables to the random sample we need. Our results shows that any one of the generalized inverses defined above will work as the quantile transformation.
2. Relations between the Four Generalized Inverses
Four generalized inverse of a distribution function were introduced in last section. In this section we prove the following relations between them.
Theorem 1. The four generalized inverses of  defined above satisfy
defined above satisfy

Proof. For any , if
, if , then
, then
 , therefore
, therefore , which means
, which means . For any
. For any , from the definition of
, from the definition of , we have
, we have . Therefore
. Therefore , which means
, which means
 . It’s obvious that
. It’s obvious that . If
. If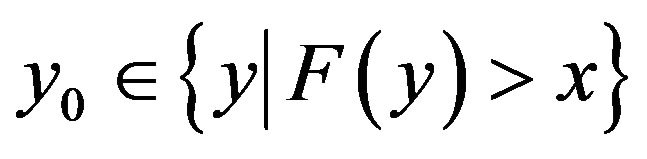 , then
, then , therefore
, therefore , which means
, which means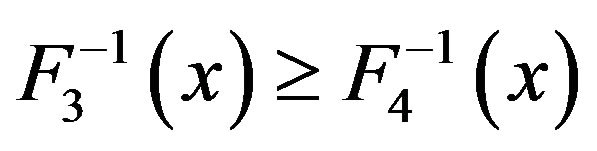 . For any
. For any
 , from the definition of
, from the definition of , we have
, we have
 . Then
. Then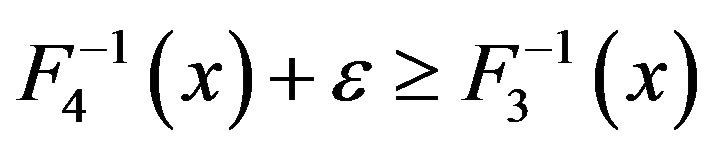 , which means
, which means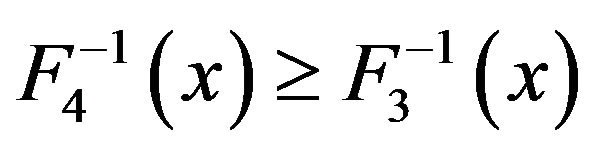 . □
. □
Remark. Theorem 1 shows that there are actually only two distinct versions of the generalized inverse of  defined in Section 1. The generalized inverse
defined in Section 1. The generalized inverse  widely used in literature (e.g. [4], p. 113) is the smaller one. The asymptotic property of sample quantiles based on
widely used in literature (e.g. [4], p. 113) is the smaller one. The asymptotic property of sample quantiles based on  have been studied extensively in statistical literatures (e.g. [4], p. 113). However, the asymptotic property of sample quantiles based on
have been studied extensively in statistical literatures (e.g. [4], p. 113). However, the asymptotic property of sample quantiles based on 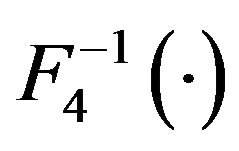 has not been reported. It’s reasonably to conjecture that it should have the same asymptotic properties as that based on
has not been reported. It’s reasonably to conjecture that it should have the same asymptotic properties as that based on .
.
3. Right Continuity
The distribution function F is right continuous. We want to know if its generalized inverses are also right continuous. Here is the result for its two versions of generalized inverses.
Theorem 2.  is right continuous. Generally
is right continuous. Generally 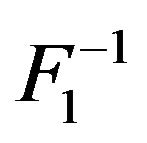 is not right continuous.
is not right continuous.
Proof. We first prove that  is right continuous by contradiction. Suppose not. Then there exist
is right continuous by contradiction. Suppose not. Then there exist  and
and  such that
such that

Then . Hence there exist
. Hence there exist  such that
such that . Therefore
. Therefore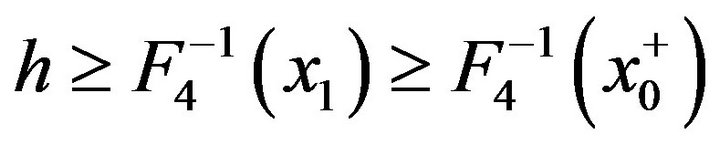 . A contradiction.
. A contradiction.
As for , let
, let 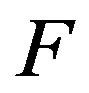 be defined as
be defined as

Then for any . □
. □
Remark 1.  is called the right-continuous version inverse of
is called the right-continuous version inverse of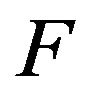 . The right-continuity property of both the distribution function and its quantile transform based on
. The right-continuity property of both the distribution function and its quantile transform based on  shows a symmetric property between these two functions. Marshall and Olkin [8] gave an nice introduction to the generalized inverse of a distribution function and prove that
shows a symmetric property between these two functions. Marshall and Olkin [8] gave an nice introduction to the generalized inverse of a distribution function and prove that  was right continuous in a different way. However, they did not give the inequalities in our Theorem 1.
was right continuous in a different way. However, they did not give the inequalities in our Theorem 1.
Remark 2. There are some mistakes in statistical literatures about the continuity properties of generalized inverse of distribution functions. For example, Andersen et al. (1993, p. 274) stated that 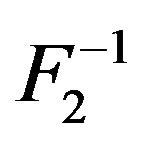 was the rightcontinuous inverse of F. According to our Theorem 2, their claim is incorrect.
was the rightcontinuous inverse of F. According to our Theorem 2, their claim is incorrect.
4. Generalized Inverse and Quantile Transformation
In this section we assume that F is a PDF. It’s well known that if U is uniformly distributed on , then the random variable
, then the random variable  has distribution function F. Durrett [9] gives a nice proof. In his proof, he constructed a probability space
has distribution function F. Durrett [9] gives a nice proof. In his proof, he constructed a probability space , where
, where  ,
,  is the Borel
is the Borel  -field on
-field on , and P is the Lebesgue measure. For each x, define two sets
, and P is the Lebesgue measure. For each x, define two sets
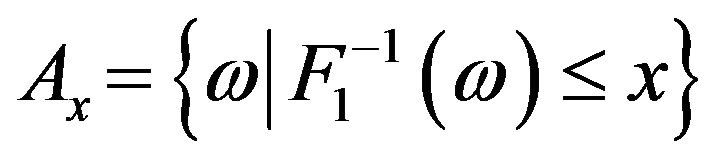 and
and . It’s easy to prove that
. It’s easy to prove that . Then
. Then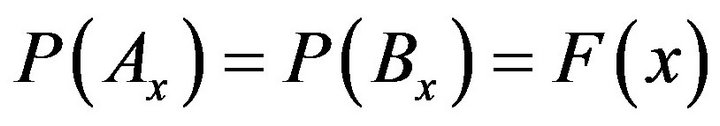 . We have similar result for
. We have similar result for .
.
Theorem 3.  has distribution function
has distribution function .
.
Proof. Following the same idea of Durrett (2010), for any x, define .
.
It’s easy to prove that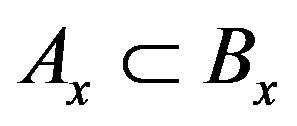 . In general,
. In general, . However, if we define
. However, if we define , then
, then
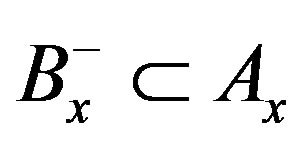 . For if
. For if , then
, then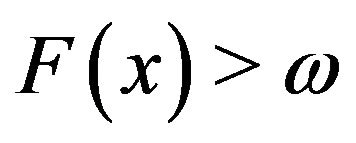 , i.e.
, i.e.
 . As
. As , we have
, we have
 . □
. □
5. Conclusion
In this paper we study the relations of four popular generalized inverses of a general distribution functions and their right-continuity properties. Our results indicate that the generalized inverse  widely used in literature may be not right continuous. We also prove that for a PDF
widely used in literature may be not right continuous. We also prove that for a PDF ,
,  is a valid quantile transformation which has one more property (right continuity) than the quantile transformation
is a valid quantile transformation which has one more property (right continuity) than the quantile transformation  which is currently used. One remaining problem is to show that the sample quantile based on
which is currently used. One remaining problem is to show that the sample quantile based on  has the same asymptotic properties as that based on
has the same asymptotic properties as that based on . Since both
. Since both  and
and  as reasonable generalized inverse of F, their average
as reasonable generalized inverse of F, their average
 should also be a good candidate of generalized inverse. The properties of this now function deserves further exploration.
should also be a good candidate of generalized inverse. The properties of this now function deserves further exploration.
6. Acknowledgements
This research was supported by grants 5U19AI056390- 05 and 3 UL1 RR024160-02S1 from the National Institutes of Health.
NOTES