1. Introduction
There are many methods to obtain explicit solutions of nonlinear evolution equations, such as the inverse scattering transformation (IST) [1], Bäcklund transformation [2], Darboux transformation [3], Painlevé analysis method [4], etc. [5-8]. Among these methods, DT is a useful method which is a special gauge transformation transforming a linear problem into itself. Many different forms of DTs have been considered in [9-19]. Generally, there are two kinds for the DTs of Lax pairs. One is to give 1-fold form Darboux matrix and obtain the N-th solution by iterating N times [14-16]. The other is to directly construct N-fold form Darboux matrix and obtain the N-th solution without iteration [17-19].
In this paper, according to the form of a Lax pair and the properties of solutions, we consider the relations between the above two kinds of DTs by considering the Lax pair given in [16]. We construct the N-fold DT for the Lax pair, which simplifies the complicated process of iterating 1-fold form Darboux matrix and gives the relationship between the trivial solution and the general solutions. The main idea of this paper comes from the reduction of DT in [20] and the determinant representation of Darboux transformation for AKNS system in [21].
In Section 2, from a Lax pair in [22], we deduce several nonlinear evolution equations. For a special case, we give the N-fold DT. In Section 3, we give the N-fold Darboux matrix and the relationship between new and old potentials. In Section 4, we obtain exact solutions of the nonlinear evolution equations and discuss the properties of these solutions. In Section 5, we make our conclusion.
2. Soliton Equations
We consider the isospectral problem introduced in [22]
 (2.1)
(2.1)
and the auxiliary spectral problem
 (2.2)
(2.2)
where
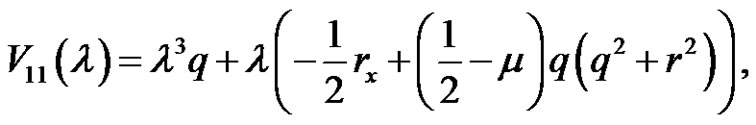
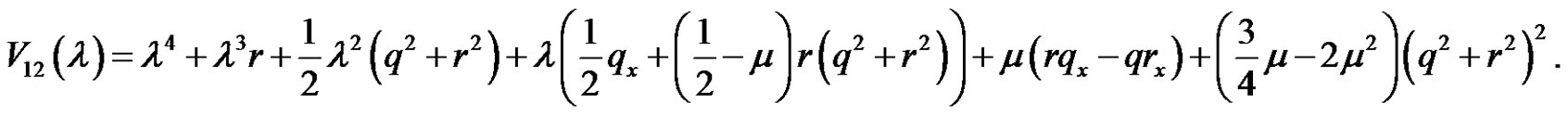
By using of the zero curvature equation

We get a new nonlinear evolution equation
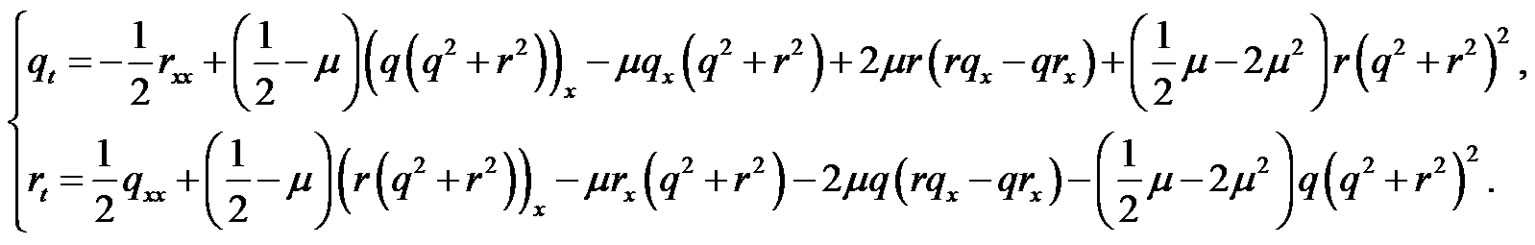 (2.3)
(2.3)
Letting , the above system reduces to a generalized derivative nonlinear SchrÖdinger (GDNS) equation
, the above system reduces to a generalized derivative nonlinear SchrÖdinger (GDNS) equation
 (2.4)
(2.4)
If , the above equation reduces to the derivative nonlinear SchrÖdinger (DNS) equation which describes the propagation of circular polarized nonlinear Alfvén waves in plasmas [23].
, the above equation reduces to the derivative nonlinear SchrÖdinger (DNS) equation which describes the propagation of circular polarized nonlinear Alfvén waves in plasmas [23].
We consider the Darboux transformation of the Lax pair (2.1) and (2.2). In this paper, we find the Darboux transformation for the case of . In this case, from
. In this case, from
(2.3), we have
 (2.5)
(2.5)
and when , the above system becomes
, the above system becomes
 (2.6)
(2.6)
In which  means the conjugate of u.
means the conjugate of u.
In [16], 1-fold Darboux matrix has been given and by applying it N times, a series of explicit solutions are obtained. Also, the relationship between
 and
and  is given. By using of this relationship, if we want to get
is given. By using of this relationship, if we want to get , we have to deduce
, we have to deduce 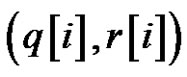 for
for . This is very complicated. The purpose of this paper is to improve this process and obtain the relationship between the trivial solution
. This is very complicated. The purpose of this paper is to improve this process and obtain the relationship between the trivial solution  and the new solution
and the new solution  by constructing N-fold Darboux matrix.
by constructing N-fold Darboux matrix.
3. Darboux Transformation
We first introduce a transformation
 (3.1)
(3.1)
for the spectral problem (2.1), where T satisfies
 (3.2)
(3.2)
Note that  and U have the same form except that q and r are replaced by
and U have the same form except that q and r are replaced by  and
and , respectively, in (2.1).
, respectively, in (2.1).
According to the forms of (2.1) and (2.2), we find that if  is a solution with
is a solution with ,
,  is a solution with
is a solution with . Then we suppose that T has the following form
. Then we suppose that T has the following form
 (3.3)
(3.3)
where  and
and 
 are functions of x and t.
are functions of x and t.
Let
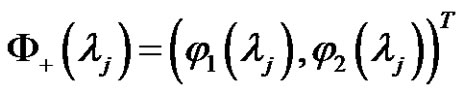
and

be two basic solutions of (2.1) and (2.2) with . Then
. Then
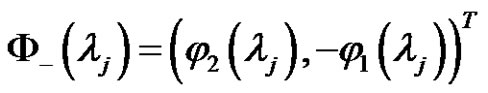
and

are two basic solutions of (2.1) and (2.2) with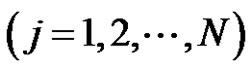
 . From (3.3), we find that
. From (3.3), we find that
 (3.4)
(3.4)
which means that  and
and  are roots of
are roots of .
.
From (3.1), we find that  and
and  satisfy the following linear algebraic system
satisfy the following linear algebraic system
 (3.5)
(3.5)
where
 (3.6)
(3.6)
with 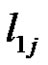 and
and 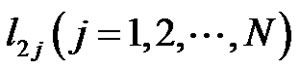 are constants.
are constants.
Proposition 3.1 Through the transformation (3.1) and (3.2), 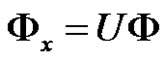 becomes
becomes  with
with
 (3.7)
(3.7)
and
 (3.8)
(3.8)
Proof. Let 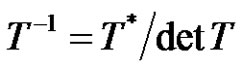 (
( means the adjoint matrix of T) and
means the adjoint matrix of T) and
 (3.9)
(3.9)
It is easy to see that  and
and  are (2N + 1)th-order polynomials of
are (2N + 1)th-order polynomials of  and
and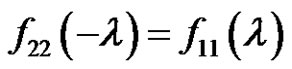 . Also,
. Also,  and
and  are (2N + 2)th-order polynomials of
are (2N + 2)th-order polynomials of 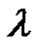 and
and When
When
 together with (2.1) and (3.6), we obtain a Riccati equation
together with (2.1) and (3.6), we obtain a Riccati equation
 (3.10)
(3.10)
After calculation, we find that all  are roots of
are roots of . Hence we have
. Hence we have
 (3.11)
(3.11)
where
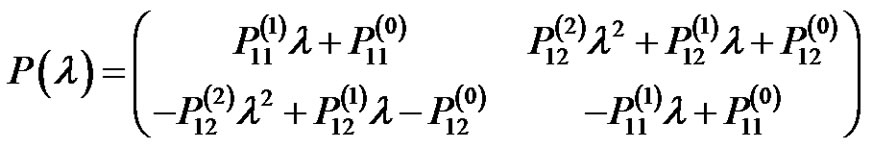
and  are independent of
are independent of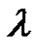 . Then we have
. Then we have
 (3.12)
(3.12)
Comparing the coefficients, we have

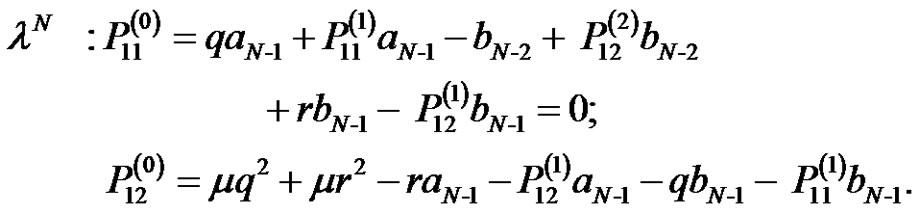
We find that , that is
, that is  if and only if
if and only if . The proof is complete.
. The proof is complete.
Remark 3.1 The proof of Proposition 3.1 is similar to that in [18]. Due to the property of basic solutions of the Lax pair (2.1) and (2.2), the proof here is more tricky.
Proposition 3.2 From the transformation (3.1) and  together with
together with ,
, 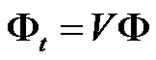
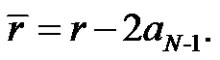
 is transformed into
is transformed into , where
, where  has the same form as V with q and r replaced by
has the same form as V with q and r replaced by  and
and , respectively.
, respectively.
Remark 3.2 The proof of Proposition 3.2 is similar to Proposition 3.1 and we omit it here for brevity.
According to Proposition 3.1 and 3.2, from the zero curvature equation , we find that both
, we find that both 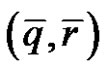 and (q, r) satisfy (2.5). The transformation (3.1) and (3.8) is called the Darboux transformation of (2.5). Then we have the following theorem.
and (q, r) satisfy (2.5). The transformation (3.1) and (3.8) is called the Darboux transformation of (2.5). Then we have the following theorem.
Theorem 3.1 The solution (q, r) of (2.5) are mapped into the new solution  through the Darboux transformation (3.1) and (3.8), where
through the Darboux transformation (3.1) and (3.8), where  and
and 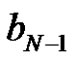 are determined by (3.5). And
are determined by (3.5). And  is a new solution of (2.6).
is a new solution of (2.6).
Proof. On one hand, according to the Proposition 3.1 and 3.2, together with the transformation (3.1), we know that (q, r) is a solution of (2.5), and  is another solution of (2.5). On the other hand, if (q, r) is a solution of (2.5), then
is another solution of (2.5). On the other hand, if (q, r) is a solution of (2.5), then  is a solution of (2.6). So,
is a solution of (2.6). So,  is a new solution of (2.6).
is a new solution of (2.6).
4. Explicit Solutions
In this section, we apply the Darboux transformation (3.1) and (3.8) to get explicit solutions of (2.5).
To compare with the solutions obtained in [16], we start from the same trivial solution (q[0], r[0]) = (0,0) and select basic solutions
 (4.1)
(4.1)
and
 , (4.2)
, (4.2)
where  and
and  are constants. Then
are constants. Then
 (4.3)
(4.3)
From the linear algebraic system (3.5), we have
 , (4.4)
, (4.4)
where
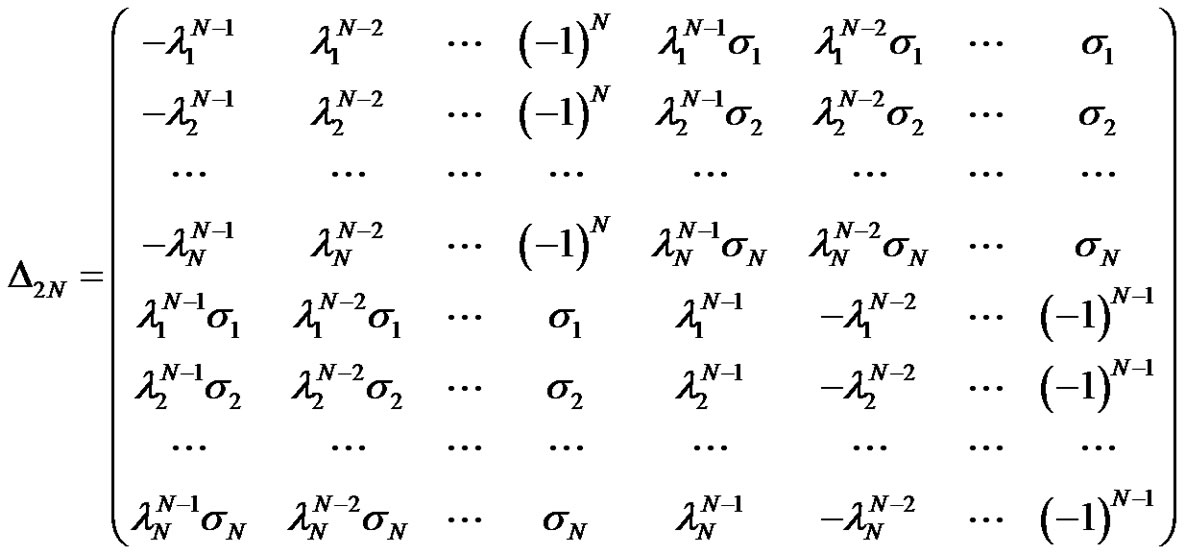
and  are obtained by replacing 1-st and (N + 1)-th columns with
are obtained by replacing 1-st and (N + 1)-th columns with
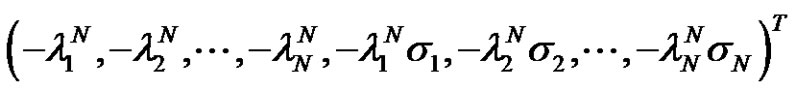
in  respectively.
respectively.
Then, according to the Theorem 3.1 and above analysis, the solution of nonlinear evolution Equation (2.5) is
 (4.5)
(4.5)
and the solution of (2.6) is
 . (4.6)
. (4.6)
In [16], the relationship of  and
and  is given. However, the Darboux transformation obtained here gives the relationship between
is given. However, the Darboux transformation obtained here gives the relationship between
 and
and , which is more direct and universal to get solutions.
, which is more direct and universal to get solutions.
For N = 1, we have
 ,
,  , (4.7)
, (4.7)
then
 (4.8)
(4.8)
 . (4.9)
. (4.9)
For N = 2, we have
 (4.10)
(4.10)
 (4.11)
(4.11)
then
 (4.12)
(4.12)
 (4.13)
(4.13)
where



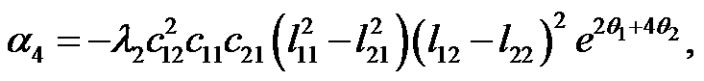
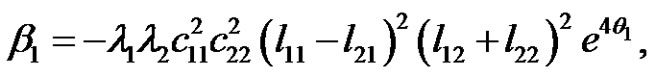

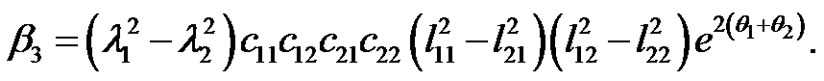
If we let 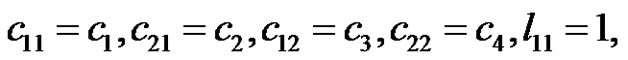
 , solutions
, solutions  and
and
 are exactly the same as the solutions in [16].
are exactly the same as the solutions in [16].
In general, according to [21], we know that the N-fold Darboux transformation is an action of the n-times repeated 1-fold Darboux transformation. The solution  are the same as the solution in [16] in essence. The matrix T can be expressed by the determinant of basic solutions
are the same as the solution in [16] in essence. The matrix T can be expressed by the determinant of basic solutions
 (4.14)
(4.14)
where
 ,
,  ,
,
 ,
, 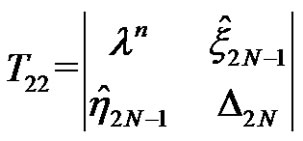
with
 ,
,
 ,
,
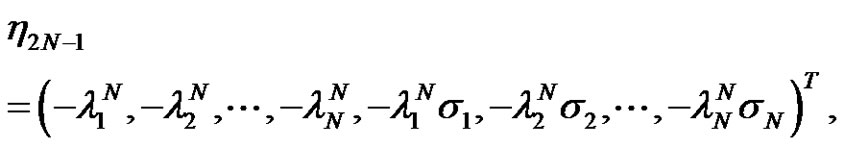
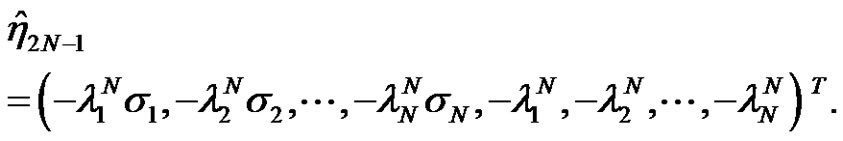
The matrix T is the same as (3.3), which is also consistent with the Darboux matrix in [21].
5. Conclusion
In this paper, for a Lax pair which is not the AKNS system, we give a N-fold Darboux transformation, coefficients of this matrix can be obtained from a algebraic system and expressed with rank-2N determinants. The Darboux transformation gives the relationship between  and
and 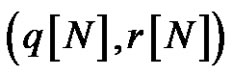 The advantage of this method is that it is more direct and universal to get explicit solutions of (2.5) and (2.6).
The advantage of this method is that it is more direct and universal to get explicit solutions of (2.5) and (2.6).