Dynamic Deformation Electron-Phonon Interaction in Disordered Bulk Semiconductor ()
1. Introduction
Electron-phonon interaction (e-ph) has drawn immense interest in the recent past [1-7]. The e-ph interaction in disordered metals has been extensively studied theoretically, by a good number of authors for over three decades, but quite different predictions were concluded [8]. For example, values for the temperature exponent (p) ranging from 2 to 4 have been predicted. Experimentally, the temperature dependence of 1/tph reported by various measurements on various material systems is not always in agreement with one another. This issue becomes even more delicate when one is concerned with the disorder behavior of 1/tph. On one hand, theories have predicted distinctly different disorder dependence of 1/tph, and on the other hand, few experiments in literature have succeeded in reporting a clear dependence of 1/tph on disorder. The electron-phonon interaction in disordered systems is due to two process: a) the pure electron-phonon scattering (the only mechanism of the electron-phonon interaction in pure metals), and b) the inelastic electron scattering from vibrating impurities (defects, boundaries, etc). The last mechanism combined with the elastic electron scattering and electron-phonon scattering, generates a variety of interference processes [9].
Interaction between electrons and phonons is strongly affected by the disorder of the electron system and, therefore, the problem is commonly divided into two special cases: the pure and impure (or diffusive) limit. The crossover between these two limits is defined by ql = 1, where q is the phonon wave vector and l is the electron mean free path. When the whole phonon system is considered, then the phonon wave vector can be conveniently replaced by the thermal phonon wave vector, 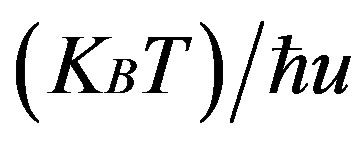
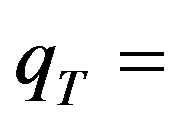 where T is the temperature of the lattice and u is the sound velocity. The e-ph interaction in disordered semiconductors is much more complicated than in pure bulk systems. Despite the progress in theory the issue has not been settled completely yet [10]. Sergeev et al. have obtained analytical results on the e-ph scattering rates via the Deformation Potential (DP) for single valley disordered semiconductor bulk and nanostructures [7]. They predict that the e-ph energy relaxation is strongly enhanced when the system enters from the pure limit (ql > 1) to the diffusive limit (ql < 1). Various temperature (T) and mean free path (l) dependences have been determined in the static screening condition. The behavior is the opposite in comparison to metals where it is well known, since the pioneering work by Pippard [11], that the disorder of the electron system tends to suppress the e-ph energy relaxation. In semiconductors, due to small electron density, the e-ph interaction can be described by deformation potential coupling constants, which do not depend on the electronic variables, while in metals the coupling strongly depends on the electron momentum [12]. Chow et al. studied that the phonon emission power in dirty sample is significantly enhanced due to disorder induced change in the screening from static to dynamic [13]. Other studies have also highlighted the significance of dynamic screening [14-17]. Yu et al. [18] presented a detailed experimental investigation of the effects of disorder on the electron-phonon interaction in semiconducting InN system. Both the temperature (T) and disorder (electron mean free path l) dependences of the electron-phonon scattering time
where T is the temperature of the lattice and u is the sound velocity. The e-ph interaction in disordered semiconductors is much more complicated than in pure bulk systems. Despite the progress in theory the issue has not been settled completely yet [10]. Sergeev et al. have obtained analytical results on the e-ph scattering rates via the Deformation Potential (DP) for single valley disordered semiconductor bulk and nanostructures [7]. They predict that the e-ph energy relaxation is strongly enhanced when the system enters from the pure limit (ql > 1) to the diffusive limit (ql < 1). Various temperature (T) and mean free path (l) dependences have been determined in the static screening condition. The behavior is the opposite in comparison to metals where it is well known, since the pioneering work by Pippard [11], that the disorder of the electron system tends to suppress the e-ph energy relaxation. In semiconductors, due to small electron density, the e-ph interaction can be described by deformation potential coupling constants, which do not depend on the electronic variables, while in metals the coupling strongly depends on the electron momentum [12]. Chow et al. studied that the phonon emission power in dirty sample is significantly enhanced due to disorder induced change in the screening from static to dynamic [13]. Other studies have also highlighted the significance of dynamic screening [14-17]. Yu et al. [18] presented a detailed experimental investigation of the effects of disorder on the electron-phonon interaction in semiconducting InN system. Both the temperature (T) and disorder (electron mean free path l) dependences of the electron-phonon scattering time  have been determined from the weak localization analysis. They have found
have been determined from the weak localization analysis. They have found  exhibits a tendency to change gradually from that the characteristic dependence
exhibits a tendency to change gradually from that the characteristic dependence  µ T3l0 in the pure limit to the form of T2l−1 as the films become disordered. Their observation gives clear evidence for the substantial enhancement of the electron-phonon coupling in semiconductor structures due to elastic electron scattering. Recently, J. T. Muhonen et al. have focused on the signifycance of the electron-phonon energy loss rate in a manyvalley semiconductor system due to lattice mismatch induced strain [19].
µ T3l0 in the pure limit to the form of T2l−1 as the films become disordered. Their observation gives clear evidence for the substantial enhancement of the electron-phonon coupling in semiconductor structures due to elastic electron scattering. Recently, J. T. Muhonen et al. have focused on the signifycance of the electron-phonon energy loss rate in a manyvalley semiconductor system due to lattice mismatch induced strain [19].
In view of these aforementioned points, we investigated the electron phonon rate in disordered three dimensional electron gas (3DEG) confined to GaAs system interacting with bulk (3D) phonons in the full diffusive limit incorporating the dynamic DP, to determine by what degree and character the dynamical behavior of these functions influences the electron-phonon scattering rate. The paper is organized as follows: Section 2 describes the formalism; Section 3 contains the results and discussion and lastly; Section 4 concludes the work.
2. Formalism
The e-ph relaxation rate,  is determined by the following kinetic equation [17]:
is determined by the following kinetic equation [17]:
 (1)
(1)
where 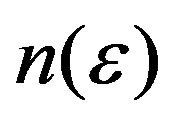 is the non equilibrium electron distribution function in a spatially uniform system. In equilibrium, phonon and electron distribution functions respectively are
is the non equilibrium electron distribution function in a spatially uniform system. In equilibrium, phonon and electron distribution functions respectively are  and
and , and the
, and the  at the Fermi surface
at the Fermi surface  is given by
is given by
 (2)
(2)
where t is the relaxation time for electron-impurity scattering, 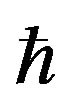 is the Planck’s constant, q is the 3D phonon momentum,
is the Planck’s constant, q is the 3D phonon momentum,  is the 3D electronic density of states; m* is the effective electronic mass,
is the 3D electronic density of states; m* is the effective electronic mass,
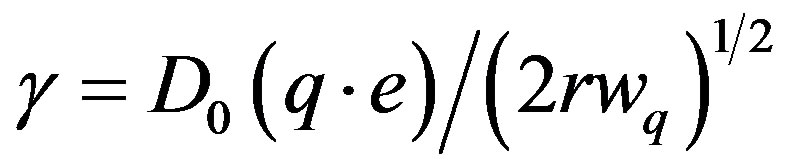 is the vertex of the unscreened electron acoustic phonon DP interaction, D0 is the coupling constant of DP, e is the polarization vector, r is the density of the material, wq = |q|u, is the linear phonon dispersion, u is the longitudinal sound velocity,
is the vertex of the unscreened electron acoustic phonon DP interaction, D0 is the coupling constant of DP, e is the polarization vector, r is the density of the material, wq = |q|u, is the linear phonon dispersion, u is the longitudinal sound velocity,
 is the phonon distribution function at equilibrium,
is the phonon distribution function at equilibrium,  is the electron distribution function at equilibrium,
is the electron distribution function at equilibrium,  is the dynamic dielectric function, and
is the dynamic dielectric function, and
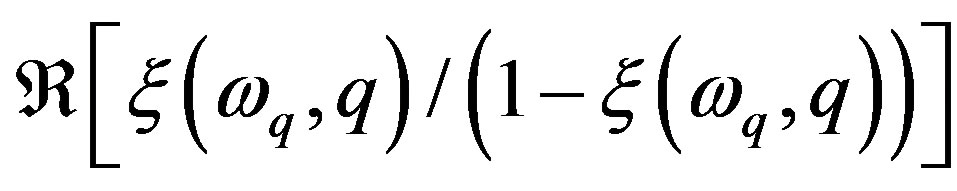 is the real part of the polarization function that has been obtained by simplifying the response functions [7]. The dynamic screening of DP is described in terms of the dynamic dielectric function which is given by;
is the real part of the polarization function that has been obtained by simplifying the response functions [7]. The dynamic screening of DP is described in terms of the dynamic dielectric function which is given by;
 (3)
(3)
in which  is the 3D Fourier transform of the bare Coulomb potential, e is the electronic charge, e0 is the background dielectric constant, and
is the 3D Fourier transform of the bare Coulomb potential, e is the electronic charge, e0 is the background dielectric constant, and  is the polarization operator. In the limit of small q and w, the dielectric function in the diffusive limit is given by [20].
is the polarization operator. In the limit of small q and w, the dielectric function in the diffusive limit is given by [20].
 (4)
(4)
where  is the 3D diffusion constant. The dynamic polarization function for 3DEG is obtained as [7];
is the 3D diffusion constant. The dynamic polarization function for 3DEG is obtained as [7];
 (5)
(5)
For, 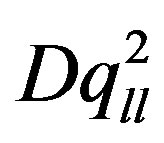

 , the
, the  -dependence of the dielectric function in Equation (4) can be dropped to yield the statically screened dielectric function,
-dependence of the dielectric function in Equation (4) can be dropped to yield the statically screened dielectric function,
 (6)
(6)
where . The dynamic polarization function in Equation (5) in the static limit reduces to
. The dynamic polarization function in Equation (5) in the static limit reduces to
 (7)
(7)
The electron-phonon rates have been calculated in Ref. [7] from Equation (2) by substituting, static dielectric function , which is a result of static polarization function
, which is a result of static polarization function . In terms of dimensionless parameters;
. In terms of dimensionless parameters;
 ,
,  and
and , where
, where
 and
and  are the Boltzmann’s and Planck’s constants respectively,
are the Boltzmann’s and Planck’s constants respectively,  is the inverse screening length [17], the Equation (2) takes the form;
is the inverse screening length [17], the Equation (2) takes the form;
 (8)
(8)
The analytical result under strong screening for the case 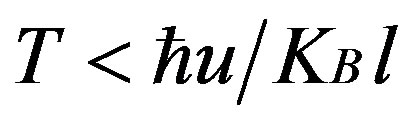 is reproduced here from Ref. 7, for the ease of reference,
is reproduced here from Ref. 7, for the ease of reference,
 (9)
(9)
3. Results and Discussion
The approximate analytical evaluation of Equation (1) cannot be a replacement for a full numerical treatment of the concerned equation. In order to see the complete effects of dynamic DP on temperature and disorder we took recourse to numerical computation, as in Ref. 7 only approximate analytical results in the static weak and strong screening and impurity limit respectively have been obtained. The electron-phonon scattering rates is computed as a function of T, l and carrier density (N) for disordered 3DEG confined to GaAs system that has been modeled in terms of the following material parameters; D0 = 8.0 eV,  , u = 5.2 × 105 cm/S, r = 5.2 gm/cm3, m* = 0.067 m, and electron density N = 5 × 1017 cm–3. This electron density corresponds to the Bloch-Gruneisen temperature limit of 19.50 K. Figure 1 presents (a) the extracted exponent of temperature p and (b) the e-ph scattering rate (
, u = 5.2 × 105 cm/S, r = 5.2 gm/cm3, m* = 0.067 m, and electron density N = 5 × 1017 cm–3. This electron density corresponds to the Bloch-Gruneisen temperature limit of 19.50 K. Figure 1 presents (a) the extracted exponent of temperature p and (b) the e-ph scattering rate ( ) for a fixed value of mean free path (l = 10 nm) as a function of temperature. The curve A displays the analytical result of Equation (9) under static screening case. Curves B and C of Figure 1(b), has been obtained by computing Equation (2) and Equation (8) incorporating the static and dynamic dielectric functions respectively. We observe that the power exponent (p) of temperature varies from T6.134 to T3.95, for the lower and upper values of plotted range of temperature. It is observed from the Figure 1(b) that the analytical curve A and the numerical dynamic result B and static result C merge with each other for values of temperature less than 5 K but above this temperature the curves B & C together trace a different path from that of the analytical curve A. To investigate the behaviors of e-ph rate with disorder, we plotted in Figure 2, the variation of electron-phonon scattering rate with mean free path (l) for a fixed value of temperature T = 10 K. Curve A of Figure 2 is plotted for the analytical static case from Equation (9) and curves B and C are plotted for numerically static and dynamic case.
) for a fixed value of mean free path (l = 10 nm) as a function of temperature. The curve A displays the analytical result of Equation (9) under static screening case. Curves B and C of Figure 1(b), has been obtained by computing Equation (2) and Equation (8) incorporating the static and dynamic dielectric functions respectively. We observe that the power exponent (p) of temperature varies from T6.134 to T3.95, for the lower and upper values of plotted range of temperature. It is observed from the Figure 1(b) that the analytical curve A and the numerical dynamic result B and static result C merge with each other for values of temperature less than 5 K but above this temperature the curves B & C together trace a different path from that of the analytical curve A. To investigate the behaviors of e-ph rate with disorder, we plotted in Figure 2, the variation of electron-phonon scattering rate with mean free path (l) for a fixed value of temperature T = 10 K. Curve A of Figure 2 is plotted for the analytical static case from Equation (9) and curves B and C are plotted for numerically static and dynamic case.
 (a)
(a) (b)
(b)
Figure 1. (a) Values of p as a function of temperature (T); (b) Electron-phonon scattering rate (te-ph–1) versus temperature for electron mean free path (l = 10 nm). Curve A displays the analytic result reported in [7]. Curves B & C are plotted numerically by taking static and dynamic screening from Equations (2) & (8), respectively.

Figure 2. Electron-phonon scattering rate (te-ph–1) as a function of mean free path (l). Curve A displays the analytic result reported in [7] at T = 10 K. Curves B & C are plotted numerically by taking static and dynamic screening from Equations (2) & (8), respectively.
It is noticed from Figure 2 that the analytical curve A varies inversely with mean free path (l) but the numerical curves B & C deviate from this strict inverse behavior. These curves A, B & C come close together for higher values of (l) and separate out from each other in the opposite limit of decreasing (l). The variation of the electron-phonon scattering rate with carrier density N can be seen in the Figure 3 which is plotted at a temperature of 10 K. Again the analytical curve A is observed to vary inversely with carrier density (N). However, the numerical curves B & C departs from this linear behavior as has been the case in the above two figures. The differences between the analytical and numerical static and numerical dynamic is best highlighted in this figure. All this three figures corroborate the results produced in each of them. Therefore, clearly this comparative theoretical study of the electron-phonon scattering rate with the static and dynamic screening shows that the dynamic screening cannot be ignored as it significantly modifies the magnitude and behavior of electron-phonon scattering rate in disordered bulk semiconductor system.
4. Conclusion
The temperature and mean free path variation of (te-ph–1) depend strongly on disorder. The character of the electronphonon interaction via the deformation potential (DP) is affected significantly by the inclusion of the dynamic screened DP and the polarization operator. On inclusion of dynamic screened DP the temperature exponent is enhanced at lower temperatures and reduces at higher temperatures from that of the analytical T6 result obtained under the statically screened DP approximation. The magnitude is also reduced at higher temperature. Further the dynamically screened electron-phonon scattering rate is
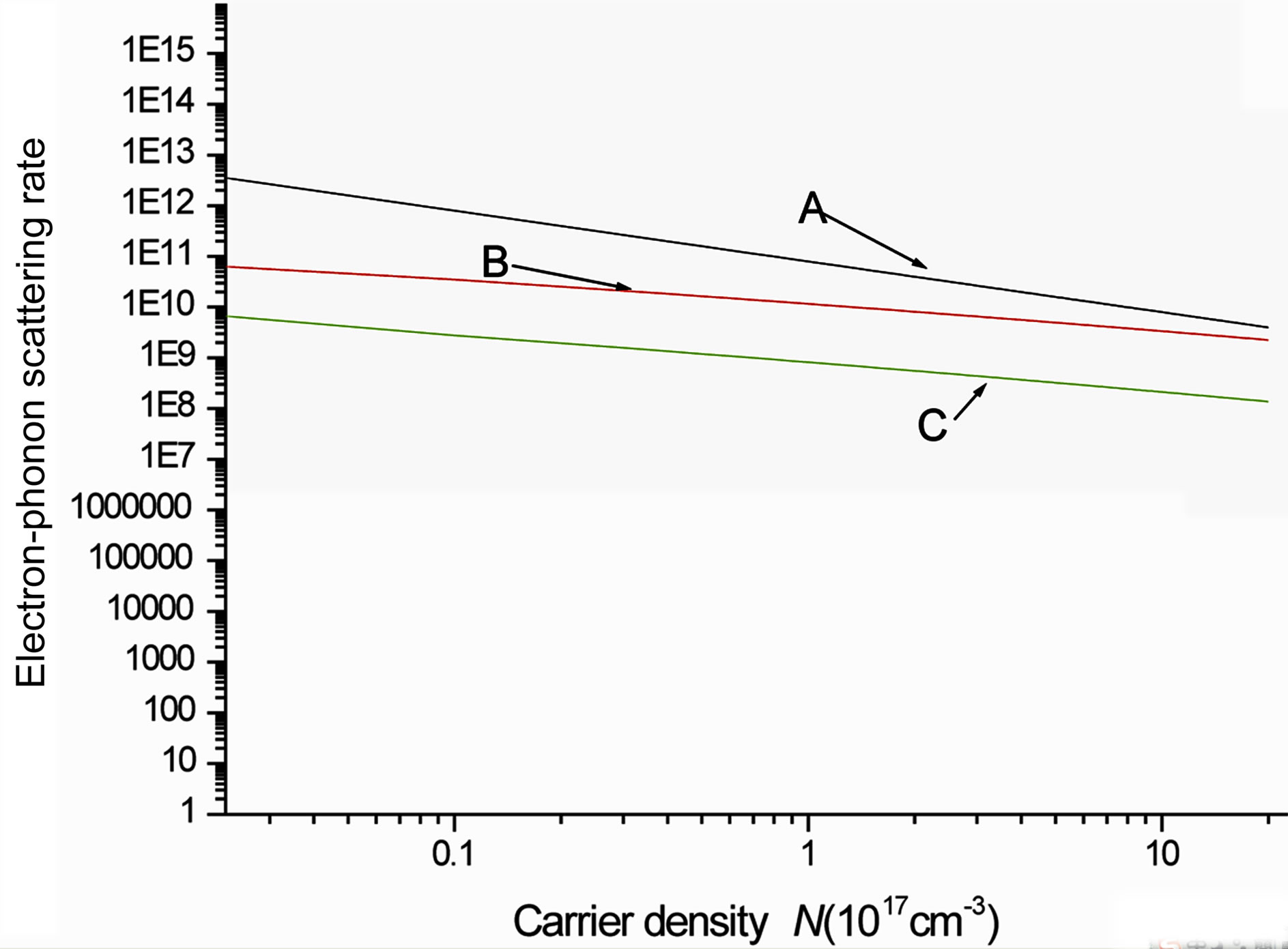
Figure 3. Electron-phonon scattering rate (te-ph–1) as a function of electron density (N). Curve A displays the analytical result reported in [7] at T = 10 K and l = 10 nm. Curves B and C are plotted numerically by taking static and dynamic screening from Equations (2) & (8), respectively.
found to decrease with mean free path too, in comparison to the earlier reported analytical calculation under static screening case. We therefore conclude from this complete numerical computation of the electron-phonon scattering rate that dynamic nature of screened DP cannot be ignored as it significantly affects the calculations and therefore governs the temperature and mean free path dependence of the electron-phonon scattering rate.
5. Acknowledgements
The authors acknowledge with thanks the financial support through the research projects sanctioned by DST, New Delhi and DAE BRNS, Mumbai.
NOTES