1. The Economics of the Pharmaceutical Industry
Pharmaceuticals is a complex industry, bound by stringent government mandates, risk averse consumer population, and an expanding cost structure of drug production and compliance. Pharmaceutical industry market size is around $700 billion. The market is geographically concentrated, with sales in the United States accounting for about 48% of the total, followed by Europe’s 29% and Japan’s 11%. Together, sales in these three regions account for slightly under 90% of the Pharmaceutical market. Since the late nineties, Pharmaceutical sales has increased by an average annual rate of 8.4%—stronger growth than the world economy in general.
Most of today’s major Pharmaceutical companies were founded in the late 19th and early 20th centuries. The industry remained relatively small scale until the 1970s when it began to expand at a greater rate. By the mideighties, Pharmaceutical manufacturing became concentrated, with a few large companies holding a dominant position throughout the world. The industry entered the 1980s pressured by economics and a host of new regulations, and transformed by new DNA chemistries and new technologies (Wikipedia, Pharmaceutical Industry). A new business atmosphere became institutionalized where the industry underwent extensive restructuring through a wave of mergers and acquisitions. This phenomenon has run parallel to the emergence of Biotechnology and Generics. Today, major trends in the Pharmaceutical industry are: continuing industry consolidation via mergers and acquisitions, research and productivity concerns, clinical and regulatory issues, increasingly high risk competition licensing and rising controversy over pricing and reimbursement [1].
A significant amount—about 20%—of the revenues in the Pharmaceutical industry are spent on the R & D of new drugs. The reasons for such high expenditure on R & D ranges from the high failure rates to high costs throughout the development phase, to resource-intensive approval process. Regulatory requirements and the use of sophisticated technologies complement these high costs. According to DiMasi of Tufts Centre for the Study of Drug Development, the cost of bringing a new drug to market (including the cost of clinical trials and failures) is estimated at around $820 millions in 2000 dollars1. These costs are roughly split equally between pre-clinical trials, clinical trials and other costs. Using confidential industry data for a selection of new drugs discovered and developed within big companies, DiMasi estimates that the average out-of-pocket cost for these drugs was just over $400 m; the rest represented the discounted opportunity cost of capital.
Pharmaceutical companies have been increasing their R & D spending by about 6% a year since 19952. Yet, productivity has not followed suit. According to European Federation of Pharmaceutical Industries and Associations (EFPIA), the chances of turning a newly discovered molecule into a successful drug is estimated at between 1/5000 - 1/10,000. For every 10,000 molecules screened, an average of 250 enter pre-clinical testing, ten make it through to clinical trials and only one makes it to market. According to Centre for Medicines Research International, since the mid-nineties, average success rates have declined, most worryingly at the later stages of clinical testing. The industry saw 24 new drugs approved by the United States Food and Drug Administration in 1998 as a result of $27 billion spent on R & D. In 2006, the industry spent $64 billion, but only 13 new drugs made it to the market3. It is also noteworthy to mention that the time it takes to bring a drug to market has increased, with the biggest rise in the clinical-trials phase. It takes an average of 12 years to develop a new drug from start to finish, depending on the nature of the molecule and of the disease it is intended to cure. This implies that drugs coming to market today reflect investment and science of a decade ago.
A 2005 study by KPMG titled “Pressure Points: Risk Management in the Pharmaceuticals Industry”, provides a comprehensive overview, highlighting the fact that the link between risk and reward has never been more important than it is now in the Pharmaceuticals industry as it grapples with the challenges of delivering profitable, new solutions for better Healthcare. The KPMG study argues that the Pharmaceutical industry is 50 percent riskier than the overall S & P 500, requiring a dramatic overhaul of risk oversight by senior management.
The present paper presents an economic analysis of the Pharmaceutical industry. Our focus is on the dynamics of firm size. It is observed that the distribution of size of firms within the industry varies as a function of time. A question of both theoretical and empirical interest is the drivers of the dynamics. To examine this question, we present and analyze a dynamic stochastic model for the evolution of density of firm size within the Pharmaceutical industry.
2. Theoretical Framework
The economics literature is rich with studies which analyze firm size heterogeneity, both within and across industry sectors. Axtell [2], Helpman, Melitz and Yeaple [3], Bottazzi and Secchi [4], Luttmer [5], Lucas [6], and Jovanovic [7], are amongst authors who have modelled the phenomena via permanent differences in firm efficiency. Hopenhayn [8], Klette and Kortum [9], Klepper and Thompson [10], and Luttmer [5] have modelled firm size dispersion via accumulated idiosyncratic shocks over a firm’s life cycle. What is relatively neglected in the literature is the dynamics of firm size outcomes across space. Yet, facts of spatial economics are surely among the most striking features of industry dynamics [11,12]. The present paper proposes a formal model to incorporate such insights.
3. The Model
Consider an industry consisting of a constant number of firms with different sizes. Average costs of producing an amount x of output are a non-increasing function of the size of the firm, for a given quality of output. Each firm may have significant fixed costs, and marginal costs may essentially be constant. Furthermore, consumers prefer small firms for perceived higher quality of service. Under these conditions, there would exist a limit equilibrium distribution of firm sizes with a certain unknown mean and variance, determined by the tension between producer and consumer preferences regarding firm size.
Consider the basic conservation law, with flux interpreted as the number of firms entering and number of firms exiting a size interval. Assume that flux is made of two opposing forces: 1) a mean reversion process interpreted as drift, and 2) a random process, interpreted as diffusion, meant to describe efficiency-induced noisy selection. Noise is generated by a passive search and learning process, based on imitation, trial and error, and learning-by-doing behavior [13,14].
More precisely, for the drift spread, it is assumed that there exists some equilibrium distribution of firm size with a certain mean and variance, towards which the ensemble of firms considered tend, governed by a velocity of adjustment4. For the diffusion spread, a search and learning process generates randomness in the system [15, 16].
In order to quantify this relationship, consider a classical linear stochastic differential equation in which the flux of probability q consists of two parts: a drift qc and some diffusion qd:
 (1)
(1)
The portion of the function transported by the drift velocity is represented by:
 (2)
(2)
and some diffusion wherein random effects cause a flux from low probability to high probability regions, following Fick’s law:
 (3)
(3)
Thus we have:
 (4)
(4)
where f denotes probability density. u denotes the mean of the distribution of firm size at equilibrium. s measures some relevant aspect of size in logarithms, and λ denotes the velocity of adjustment. ε is a constant diffusion parameter5.
4. Empirical Analysis
Our data describes the Pharmaceutical industry between the years 1989-2007. Figure 1 provides a description of the evolution of the distribution of firm sizes in the industry, where number of employees is used as proxy for size. Observations were available annually, and the sample includes 502 companies engaged in the research, development or production of Pharmaceuticals6. The vertical axis on this figure measures firm size in logarithms, and the horizontal axis measures time in years. The solid curve represents the mean size of the industry and the dotted curve one standard deviation around the mean.
Estimation
The expectation of the distribution representing the timedevelopment of the partial differential equation expressing the growth dynamics, is the first moment:
 , and the variance of the distribution,
, and the variance of the distribution,  The model has been applied to the log firm size distribution as a function of time. The initial size distribution of the population is approximated to be distributed normally about some average value
The model has been applied to the log firm size distribution as a function of time. The initial size distribution of the population is approximated to be distributed normally about some average value  on
on . This assumption, although limiting, is only chosen on grounds that it allows an analytic solution to the diffusion model. It can be removed using numerical methods. For the Ornstein-Uhlenbeck process with Fokker-Planck equa-
. This assumption, although limiting, is only chosen on grounds that it allows an analytic solution to the diffusion model. It can be removed using numerical methods. For the Ornstein-Uhlenbeck process with Fokker-Planck equa-
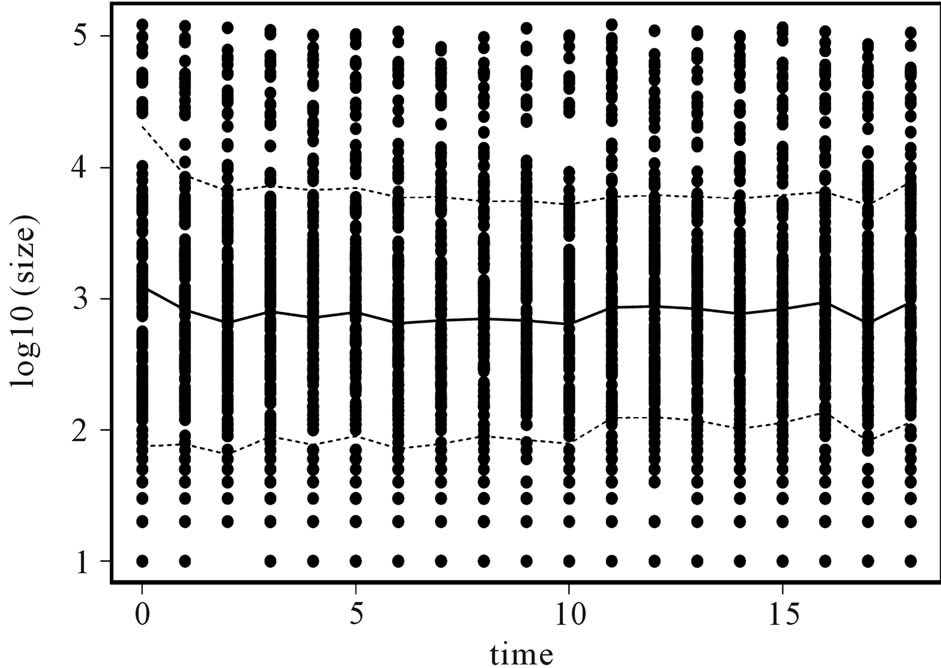
Figure 1. Evolution in distribution of firm size.
tion for the probability density, 

the rate of approach to the final equilibrium reads as 
The first and second moments have been used to estimate the five model parameters, where  denotes the initial mean of the distribution, and u denotes where the mean is heading.
denotes the initial mean of the distribution, and u denotes where the mean is heading.  represents the initial standard deviation, ε represents the diffusion parameter, and λ represents the velocity of adjustment. Table 1 reports estimates for the five model parameters
represents the initial standard deviation, ε represents the diffusion parameter, and λ represents the velocity of adjustment. Table 1 reports estimates for the five model parameters , u, ε,
, u, ε,  , and λ, along with the standard errors and t-values.
, and λ, along with the standard errors and t-values.
Figure 2 graphically illustrates the mean of the firm size distribution in the data (dotted line), superimposed on the mean of the size distribution as predicted by the model (bold solid line, +/– one standard deviation). The vertical axis on this panel measures the mean of the size distribution (in logarithms) and the horizontal axis measures time in years.
Figure 3 graphically illustrates the standard deviation of the distribution in the Pharmaceutical industry (dots), superimposed on the standard deviation of the distribution as predicted by the model (solid line).
Examining actual vs. predicted time plots can help ascertain whether the parameter estimates indeed conform to the real data presented in the descriptive analysis. Figure 4 graphically illustrates the evolution of the firm size distribution (log-normals) over time for the Pharmaceutical industry, superimposed on histograms which describe the time evolution of the distribution of firm sizes in the data (for selected years). The solid curves in these figures illustrate the distribution of firm size as predicted by the model, and the dotted curves illustrate the distribution of firm size in the data. The vertical axes in these

Table 1. Parameter estimates for the pharmaceutical industry.

Figure 3. Standard deviation of the distribution.
figures denote frequency, and the horizontal axes measure firm size in logarithms. These figures illustrate that the patterns observed in the fitted log normals are being pulled out of a set of histograms whose shape are irregular.
The results suggest that the values generated by the proposed model reliably characterize the actual data. The mean of the distribution is clearly evolving, corresponding to our theoretical predictions. The variance of the distribution is likewise evolving as expected. The distribution is approaching a long-run equilibrium and the dispersion of the distribution is shrinking over time. One might speculate that this pressure towards reduction of disparities across the industry is attributed to the velocity parameter λ. This parameter is positive as expected. The value for the diffusion parameters ε is small and positive, likewise conforming to our theoretical predictions. The diffusive limit is:  The results predict that if we start with a normal distribution and let the model drive the distribution, the distribution variance will tend toward a constant
The results predict that if we start with a normal distribution and let the model drive the distribution, the distribution variance will tend toward a constant 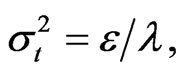 and concentrated around a mean u.
and concentrated around a mean u.
5. Conclusions
An attempt has been made to identify and quantify firm size dynamics. A stochastic model has been proposed which can be extrapolated to new and different situations. One area of investigation which would prove informative is the complex anatomy of drug R & D. The methodology presented in this paper can be fruitfully extended to map industry characteristics on the dynamics of firm structure. Such extension could shed light on the current R & D slowdown in the Pharmaceutical industry, with poignant implications for government policy with respect to patents, which are increasingly the core and foundation of the business method adopted.
The technology operated by the Pharmaceutical industry fits the non-increasing returns to scale hypothesis, under which the traditional economic model predicts that there should be many potential producers and that the industry should be dynamically competitive and innovative. Under these conditions, one would expect thriving R & D activity. This does not seem to be the case, however.
Governments are keen to help clear the industry’s bottlenecks in drug development. The European Commission, having seen much of the continent’s drug industry move its research funds across the Atlantic, is eager to help boost drug R & D at home. In the United States, the National Institutes of Health and the Food and Drug Administration have set up initiatives to push along drug discovery and development. In the academia, important theoretical and empirical work analyze the economics behind the productivity slowdown in the Pharmaceutical industry. At the forefront of such research is David Levine who has written an editorial in Expert Review of Pharmacoeconomics and Outcomes Research, arguing that stronger patents likely will not reverse the productivity slowdown in the Pharmaceutical R & D enterprise.
The issue of patents is important because in circumstances where innovations build on each other—which is the case for the discovery and development of drugs— patents can be especially costly, as they may reduce rather than encourage the incentive to innovate. The topic of patent protection in Pharmaceutical industry becomes even more crucial moving forward, as around the world,

Figure 4. Predicted vs actual distribution.
the trend points towards a Universal Intellectual Property. India has just adjusted its patent laws to comply with TRIPS requirements, with China following suit.
As early as in the early seventies, Jack Hirshleifer [22] illustrated that economically valuable information can be traded in the absence of patents and under condition of competition. More recently, Boldrin and Levine [1] use historical evidence to illustrate that intellectual property protection in Pharmaceuticals has varied enormously over time and space, and that the modern Pharmaceutical industry developed faster in those countries where patents were fewer and weaker, example Switzerland and Italy until late 1970s (see “World’s Shortest History of Pharmaceutical Patents” in Boldrin and Levine 2008, Chapter 9). Boldrin and Levine [23-26] have forcefully argued that there is no theoretical need to postulate either increasing returns or monopoly power to understand the dynamics of innovation in Pharmaceuticals, and that the traditional competitive model provides a more solid foundation for the examination of R & D processes in this industry. R & D is the life blood of the Pharmaceutical industry. The industry’s best hope lies in innovation—its traditional strength. Boldrin and Levine argue that learning and dynamic adjustment to equilibrium are weakened by obstacles such as patents, which suppress the sharing of ideas and limit the availability of material for imitation and trial-and-error. It would be worthwhile to incorporate the impact of competition and intellectual property policies on the evolution of Pharmaceutical industry. Different market structures determine different allocations of the social surplus of innovation among inventors, imitators and consumers, and hence, provide different incentives to innovate. A good understanding of which kinds of characteristics lead to which kinds of dynamics helps us better understand how incentives should be provided for the socially optimal amount of creative activity to take place.
6. Acknowledgements
Information on the Economics of the Pharmaceutical industry has been quoted from The Economist ("Testing times: Getting more out of pharmaceutical R&D", June 16, 2005), and from Wikipedia (Pharmaceutical Industry). Moreover, the author has benefited from insights offered by Omega statistical consulting regarding the empirical analysis in this paper. Parts of the statistical analysis in this paper likewise appear in Hashemi, F. (2012) Dynamics of Firm Size in Healthcare Industry. Health, 4, 155-164. doi:10.4236/health.2012.43024..
NOTES
2Centre for Medicines Research International (CMR).
3Stanford Bernstein, a New York Investment firm.
4For considerations of analytical tractability, the velocity of adjustment has been assumed constant in this study. A worthwhile extension of this model would be to allow a more realistic functional form for the velocity parameter.
5The process derived from this model evolves according to an Ornstein-Uhlenbeck. Ref [17-21] provide an elaboration albeit for different contexts.
6Our data has been compiled from Compustat. A company is assigned to a single GICS (Global Insdustry Classification Standard) according to the definition of its principal business activity as determined by Standard and Poor’s and MSCI. The 502 companies comprise the universe of all firms in the Pharmaceutical industry as reported by Compustat.