1. Introduction
The idea of space traveling intrigues humanity to wander in space beyond our solar system, within and beyond the milky way galaxy. Traveling a long distance has a major challenge-speed. Physics teaches us that speed is bounded by the speed of light. Einstein’s theory of relativity teaches us that energy in the universe is positive, yet the theory does not consider the idea of negative particles or negative energy.
*https://www.void2life.com, Void2life is a voluntary organization sharing knowledge and wisdom to promote humanity to its next level of evolution.
Alcubierre [1] spaceship cylindrical hat shape produces negative energy density everywhere.
The meaning of negative energy is debt energy. Negative dollar means a debt; it is just like the positive dollar with a negative sign reflecting a deficiency in positive cash. In that sense, negative energy shall popup whenever there is deficiency in positive energy. Recall Y.J. Segman [2] the existence of matter in the universe requires debt matter i.e. matter with negative mass reflecting asymmetric gravitation-antigravitation.
2. Preliminary
Adopting the metric model of Alcubierre [1], J. Natario [3], Eric Lentz [4] and [5] [6] and [7] with the manifold M = R4 of Cartesian coordinate system (x, y, z, t) with the metric,
(1)
With energy density E,
(2)
where the intrinsic (3)R curvature vanishes for flat metric. The volume element associated with the Eulerian observers is the trace,
(3)
and the geometric portion of the energy density E yields,
(4)
We shall explore two cases of spatial coordinate system (X, Y, Z) that provide positive energy density.
The operation conducting on the spaceship coordinate system defines the geometry of the new coordinate system and vice versa, the geometry of the coordinate system defines the operations conducting on the spaceship which in turn may provide the additional energy needed.
3. Choices of Geometry
The coordinate transformation defines the group operation related to the new coordinate system (X, Y, Z) and the vector fields associated with such group action. A shift operation reflects the movement of the spaceship over certain coordinate axis. This can be formulated as follows,
(5)
The vector fields associated with (5) is giving by the additive group generators,
(6)
Shifting coordinate system was suggested in [4] and has the following form,
(7)
(8)
(9)
Alcubierre energy density remains negative everywhere under the shifting coordinate system (Equations (7)-(9)) with
and
representing Alcubierre cylindrical hat.
(10)
The scope of this paper is to show that the movement of the spaceship over the shifting vector fields as proposed by Erik Lentz [4] may generate sufficient positive energy density overcoming debt energy. Inserting the shift vector field Equations (7)-(9) in Equation (4) yields,
(11)
where
is a mutual functional geometry in all axes X, Y and Z.
In order to have zero sum bubble wave i.e. like high pass filter reflecting high pass local wave around the spaceship, the geometry should reflect positive even function. A simple choice would be the following configuration,
for
(12)
otherwise, 0.
The coordinates are given in Equations (7)-(9) with mutual,
(13)
(14)
(15)
and
(16)
are the directional velocities in x, y and z respectively.
. (17)
Figure 1 presents the shape of the
with a = 0.5, v = 1;
![]()
Figure 1. An alien like flying saucer spaceship shape with a = 0.5 and p = 1.
Currently we are interested in two cases where p = 1 and p = 2. For Eulerian observers (Equation (3)) result in Laplace operator which yields,
(18)
For p = 1, θ = −6 av, does not depend on the spaceship radius, we may conclude that the spaceship disappears for the Eulerian observers. The energy density (Equations (2), (4) and (11)) yields,
, (19)
everywhere.
For the case p = 2 we get (Equation (18)),
(20)
And (Equation (11)):
(21)
The energy density in the center of the spaceship where r = 0 is E = 0. Moving from the center of the spaceship towards the edge where r = 1, the energy density is maximal and equal to:
(22)
Thus,
(23)
The computation for p > 2 is similar.
Figure 2 below presents the asymmetrical high pass bubble wave resulting from
in 2D i.e. xy-coordinates.
![]()
Figure 2. High pass bubble configuration
resulting from
with p= 2 and a = 0.5.
A Gaussian geometry is an additional option. Gaussian is a highly important function in signal processing since it provides an optimal time-frequency sampling window due to its characteristic of being L2 eigen function of the Fourier transform. The Laplacian of Gaussian is suggested in detection of visual motion [8] due to its configuration as edge detection high pass filter. A radial 2D Gaussian would have the following shape.
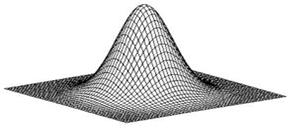 (24)
(24)
Although the function is not limited to finite interval, it tends smoothly and rapidly to zero outside.
Replacing
in Equation (12) by Gaussian geometry:
(25)
while keeping the basic model of Equations (13)-(17) with
arbitrary variables and outside the edge where r = 1 we assume 0, although the function tends rapidly to zero for large r.
The Eulerian observers are the Laplacian of the Gaussian (Figure 3),
(26)
![]()
Figure 3. Represents the Eulerian observers as Laplacian of Gaussian high pass bubble wave. The most negative value is where r = 0 (i.e. −6 avb) and the surrounding reflect positive circle wave whenever
, θ ≥ 0. The hat negative height can be configured by a and b. The bubble decays to zero for virtual large r.
The energy density:
(27)
The energy density in the spaceship center where r = 0 is
from the center the energy density is positive and decreasing towards the edge where r = 1 and
. The minimal positive energy density is in the edge and vary as the choice of b, i.e.
where
. In case
, the energy density collapse to zero. For fixed b and virtual radius r > 1, the energy becomes negative and tends to zero for large r.
If the reports of alien spaceships are adequate, then the natural geometry proposed in Equations (12), (25) may reflect alien like flying saucer spaceship fuselage.
The shifting vector field geometry given in (Equations (7)-(9)) enables sufficient positive energy. Additional potential action on the coordinate system would be scale e.g.
(28)
where,
are real positive variables. This means that the material and the construction of the spaceship should be flexible allowing certain fuselage stretching while the fuselage is designed to protect the crew members.
Coordinate rotation is an additional option and together with scaling and shifting represent group operation with vector fields associated with the linear combination of the following operators,
(29)
The local vector fields associated with scale, rotation and shift of the spaceship fuselage may enable additional positive energy density.
Scaling and shifting operations are fundamental in designing wavelet base geometry [9] - [15]. The idea of wavelets is to create sequence of functions based on scaling and shifting operation on a single mother function that would create orthogonal basis. In a way, we may look at the spaceship geometry as the mother function and the operations allowing on the spaceship coordinate system such as scaling and shifting, may support distance travel as suggested by Alcubierre [1]. This may suggest looking for wavelet geometry when allowing the spaceship fuselage to be stretched and shifted.
The above shows that Gaussian and polynomial geometry may be useful for designing spaceship warp drive. Additional potential geometry is to duplicate the geometry in both sides as shown in Figure 4.
![]()
Figure 4. Two sides geometry. (a) reflects upper and lower symmetrical configuration. (b) reflects different configuration of the upper and lower decks.
A double side configuration as presented in Figure 4 may result in the disappearing of the spaceship from Eulerian observers. Simplifying the idea, let assume that each deck incorporates independent coordinate systems, i.e., one for the upper deck and one for the lower deck. Considering, for example, Equation (26),
; (U – Upper deck) (30)
; (L – Lower deck) (31)
therefore,
. This may suggest the disappearance of the spaceship from the Eulerian observers.
4. Summary
Positive energy is feasible to achieve with the appropriate configuration as presented in this paper. Space traveling is feasible. Traveling in zero gravity requires consciousness navigation Y.J. Segman [16] and this is our aim for the next papers.
Acknowledgements
I would like to give my special thanks to Shorok, Holok and Shalley for sharing knowledge with no boundaries in the course of expending my pure consciousness.
Special thanks to Yehonatan Segman.