Approach to Riemann Hypothesis by Combined Commensurable Step Function Approximation with Bonnet Method ()
1. Introduction
In his article [1] from 1859 Bernhard Riemann expressed the conjecture (now called Riemann hypothesis) that the function
 (1.1)
(1.1)
with 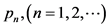 the (ordered) sequence of prime numbers and extended by him to complex variable
the (ordered) sequence of prime numbers and extended by him to complex variable 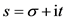 possesses nontrivial zeros only on the
possesses nontrivial zeros only on the
imaginary axis  (i.e., to real part
(i.e., to real part ) that remained unproved up to
) that remained unproved up to
now. This function was already known to Euler (Euler product) and using the uniqueness of the prime-number decompositions of natural numbers 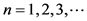 Euler established in about 1737 the connection to the sum form. Its main importance is as Riemann showed in [1] that one can derive from it approximations for the prime-number distribution. Many articles and monographs are published since this time to this function, e.g., [2] - [14] (some important original articles of the past are republished plus a few expert witnesses are published in [3] )1.
Euler established in about 1737 the connection to the sum form. Its main importance is as Riemann showed in [1] that one can derive from it approximations for the prime-number distribution. Many articles and monographs are published since this time to this function, e.g., [2] - [14] (some important original articles of the past are republished plus a few expert witnesses are published in [3] )1.
Concerning the trivial zeros of 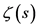 Riemann excluded them by introduction of a function
Riemann excluded them by introduction of a function 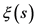 related to
related to  by
by
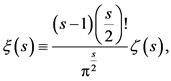 (1.2)
(1.2)
and obtained in this way the simple so-called Riemann functional equation
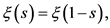 (1.3)
(1.3)
and additional symmetries. With respect to the nontrivial zeros it is fully equivalent to the zeta function 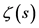 and, in addition, it excludes the only pole (a simple one) of the last at
and, in addition, it excludes the only pole (a simple one) of the last at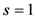 . Furthermore, the function
. Furthermore, the function ![]() possesses more symmetries than
possesses more symmetries than ![]() and is an even real-valued function on the real and imaginary
and is an even real-valued function on the real and imaginary
axis to real part ![]() in contrast to the zeta function
in contrast to the zeta function ![]() and is rapidly
and is rapidly
decreasing on the imaginary axis (and, rapidly increasing on the real axis). For more easier work with the function ![]() one may displace it according to
one may displace it according to
![]()
![]() (1.4)
(1.4)
Then the conjectured zeros lie directly on the imaginary axis.
There are many known functions with zeros only on the imaginary axis, in particular, the entire modified Bessel functions ![]()
![]() (1.5)
(1.5)
All these functions which we call here Xi functions possess integral representations of the form
![]() (1.6)
(1.6)
where we applied partial integration. With separation of the real and imaginary part we find
![]() (1.7)
(1.7)
where ![]() is a monotonically decreasing function of the real variable u and therefore with derivative
is a monotonically decreasing function of the real variable u and therefore with derivative![]() .
.
The functions ![]() are analytic even functions. We may extend the functions
are analytic even functions. We may extend the functions ![]() in the integral (1.6) to negative u by definition as symmetric functions of the real variable for
in the integral (1.6) to negative u by definition as symmetric functions of the real variable for ![]()
![]() (1.8)
(1.8)
Then we obtain by inversion of the arising Fourier integral the relation
![]() (1.9)
(1.9)
This formula provides then automatically the symmetry (1.8) of the function![]() .
.
For the Riemann Xi function ![]() the function
the function ![]() possesses the form
possesses the form
![]() (1.10)
(1.10)
as is was given in similar form in [7] (chap. 17.7, Equation (12) and Equation (14)) and in [2] and as it was also derived in [15] . For the modified entire Bessel
functions ![]() the Omega functions possess the form
the Omega functions possess the form
![]() (1.11)
(1.11)
where ![]() denotes the Heaviside step function. The continuation
denotes the Heaviside step function. The continuation
of the function ![]() to the Riemann Xi function in (1.10) from real positive variable u to real negative variable −u provides automatically the symmetry (1.8) although, astonishingly, this is not immediately to see from its given explicit form (see remark in [15] ) and also the form (1.11) for the Omega functions to modified Bessel functions possesses this symmetry.
to the Riemann Xi function in (1.10) from real positive variable u to real negative variable −u provides automatically the symmetry (1.8) although, astonishingly, this is not immediately to see from its given explicit form (see remark in [15] ) and also the form (1.11) for the Omega functions to modified Bessel functions possesses this symmetry.
Besides to be functions which rapidly decrease in a way that the integrals of the form (1.6) exist the Omega functions (1.10) and (1.11) are monotonically decreasing for ![]() and it was the conjecture in [15] that this is a common property for Xi functions to possess zeros only on the imaginary axis. For such functions the Second mean-value approach or Bonnet method of integration (e.g., Courant [16] (chap. IV), Fikhtengol’ts [17] (chap. 5, §2), Widder [18] (chap. 5)) can be applied which provides a function which depends on the initial and final values of the Omega function and which possesses in the argument a mean-value function with some known properties originating from the applied averaging process. For (1.6) assuming analyticity it possesses the form
and it was the conjecture in [15] that this is a common property for Xi functions to possess zeros only on the imaginary axis. For such functions the Second mean-value approach or Bonnet method of integration (e.g., Courant [16] (chap. IV), Fikhtengol’ts [17] (chap. 5, §2), Widder [18] (chap. 5)) can be applied which provides a function which depends on the initial and final values of the Omega function and which possesses in the argument a mean-value function with some known properties originating from the applied averaging process. For (1.6) assuming analyticity it possesses the form
![]() (1.12)
(1.12)
where ![]() denotes the lowest moment of the function
denotes the lowest moment of the function ![]() which does not depend on the reference point.
which does not depend on the reference point.
In our article [15] , apparently, this was considered correctly only up to discussion of the zeros on the imaginary axis in case of continuous Omega functions and considering the principal form of the functions for zeros on axes parallel to the imaginary axis. The last was made by actions onto the function on the imaginary axis by operators. From the correction to [15] it seems to remain correct the statement that only the monotonically decreasing step-wise constant functions with equal step-lengths have to be excluded with additional zeros. The article [19] was mainly intended to illustrate the behavior of zeros when going from lower to higher Taylor-series approximations but to the end of its elaboration it became almost evident that considering step-wise approximations of the Omega functions with commensurable step lengths2 and finally going with the step-lengths to zero is an appropriate method for considering the problem where temporal zeros in the approximations off the imaginary axis and on this axis in the limiting process go to complex infinity and there remain only the genuine zeros. To carry out this systematically is a main aim of the present article.
Since all nontrivial zeros of the Riemann zeta function can never be found explicitly this suggested from the beginning of the work that we have to look for methods which do not need the exact zeros and rest only on general properties of the considered functions and which, therefore, are true for a whole category of functions including the mentioned ones. We find that in the step-wise approach with commensurable step lengths there exist two different and well-separated kinds of zeros on the imaginary axis where the first kind possesses also zeros off the imaginary axis and in the limiting case of vanishing step lengths go to complex infinity whereas the second kind stabilizes in the limiting procedure of vanishing step lengths on the genuine zeros of the Xi functions to the considered Omega functions and, apparently, do not possess zeros off the imaginary axis (Sections 3 - 5 and also 8). This is underlined via the Second mean-value approach or Bonnet method of integration which can be successfully completed and since in this method the transition from the imaginary axis to axes parallel to the imaginary axis is possible using the Cauchy-Riemann equations in an integrated form. We repeat this approach in short form in the Sections 6 - 8 and give in Section 8, apparently relatively simple, proof that the “genuine” zeros in continuous case lie only on the imaginary axis. In Section 10, we show by example that the (strictly and non-strictly) monotonically decreasing of Omega functions in the limiting case of vanishing step lengths is a sufficient criterium for zeros only on the imaginary axis but is not a necessary one. An advantage of the mentioned methods is also that they provide arguments that step-wise constant Omega functions with incommensurable step-lengths (plus monotonically decreasing) fall also under the category for which the Xi functions possess only zeros on the imaginary axis.
2. Commensurable Step-Wise Approximations of Omega Functions to Riemann Xi Function and to Other Appropriate Xi Functions
We approximate the (in general, non-strictly) rapidly decreasing function ![]()
![]() (2.1)
(2.1)
with limiting value
![]() (2.2)
(2.2)
by a step-wise constant function with equal step lengths ![]() (a parameter which finally in a limiting procedure we let go to zero) of the following form (Figure 1)
(a parameter which finally in a limiting procedure we let go to zero) of the following form (Figure 1)
![]() (2.3)
(2.3)
where ![]() denotes the Heaviside step function (see Section 1).
denotes the Heaviside step function (see Section 1).
The integration according to (1.6) leads to
![]() (2.4)
(2.4)
where we introduced the abbreviations
![]() (2.5)
(2.5)
Due to ![]() as monotonically decreasing functions according to (2.1) they have to satisfy the inequalities
as monotonically decreasing functions according to (2.1) they have to satisfy the inequalities
![]() (2.6)
(2.6)
and due to definition (2.5) their sum is
![]() (2.7)
(2.7)
which for ![]() as indicated goes to
as indicated goes to![]() .
.
![]()
Figure 1. Approximation of the Omega function to the Riemann Xi function by a step-wise constant function with equal step length as example for such approximations. Finally we let the step length u0 go to zero. The additional zeros off the y-axis from the stepwise approximation go then to complex infinity. This procedure of step-wise approximation of a function is very similar to the usual introduction of the definite integral.
If the sequence of numbers ![]() decreases rapidly in a way that the sum in (2.5) converges for all
decreases rapidly in a way that the sum in (2.5) converges for all ![]() then the function
then the function ![]() is an entire function of the complex variable
is an entire function of the complex variable![]() . We will show that for arbitrary fixed real variable x it is a periodic function of the variable y. First, we find the periodicity
. We will show that for arbitrary fixed real variable x it is a periodic function of the variable y. First, we find the periodicity
![]() (2.8)
(2.8)
with its (minimal) period length ![]() and more generally
and more generally
![]() (2.9)
(2.9)
From this according to (2.4) results the periodicity of the function ![]()
![]() (2.10)
(2.10)
with the same period length ![]() which for arbitrary fixed x is a periodicity on all axes
which for arbitrary fixed x is a periodicity on all axes ![]() parallel to the imaginary axis
parallel to the imaginary axis ![]() and thus
and thus ![]() in the form obtained from (2.4) is a Fourier series to period length
in the form obtained from (2.4) is a Fourier series to period length![]() . For the function
. For the function ![]() this leads to
this leads to
![]() (2.11)
(2.11)
Although this is no more a periodicity of the functions ![]() their zeros repeat periodically for arbitrary fixed variable x on corresponding y-axes. Concerning these zeros they appear with half of the period of the function
their zeros repeat periodically for arbitrary fixed variable x on corresponding y-axes. Concerning these zeros they appear with half of the period of the function ![]() that means
that means
with distances ![]() on all axes
on all axes ![]() with fixed variable x parallel to the imaginary axis (the imaginary axis included).
with fixed variable x parallel to the imaginary axis (the imaginary axis included).
In the next Section we derive some more detailed representations of the Xi function ![]() which permit us to crystalize two different kinds of zeros in the considered step-wise commensurable approximation of the Omega function
which permit us to crystalize two different kinds of zeros in the considered step-wise commensurable approximation of the Omega function ![]() and call this in the further text shortly the “commensurable step-wise case”.
and call this in the further text shortly the “commensurable step-wise case”.
3. Representation of the Xi Function in Commensurable Step-Wise Case by Chebyshev Polynomials
Since ![]() is not a zero of the Xi function
is not a zero of the Xi function ![]() it is rational to investigate instead in most cases the function
it is rational to investigate instead in most cases the function![]() . We will show in next Section that in commensurable step-wise case there appear two different kinds of zeros from which the second kind is “not analytically” in a way which we will explain. Shortly saying, “not analytically” means that these zeros come from separate independent vanishing of two different functions which are not necessarily Real and Imaginary part of an analytic function of variable z. A great role plays in this case the periodicity condition (2.10).
. We will show in next Section that in commensurable step-wise case there appear two different kinds of zeros from which the second kind is “not analytically” in a way which we will explain. Shortly saying, “not analytically” means that these zeros come from separate independent vanishing of two different functions which are not necessarily Real and Imaginary part of an analytic function of variable z. A great role plays in this case the periodicity condition (2.10).
The condition for zeros in the commensurable step-wise case is the simultaneous vanishing of Real and Imaginary part of (2.4) that means the vanishing of
![]() (3.1)
(3.1)
We derive now alternative representations of this function which split from the Imaginary part a factor depending on ![]() which is not involved in the vanishing of the zeros called “not analytically”. This will be accomplished in next Section. For this purpose we use the Chebyshev polynomials of first and second kind and as preparation we consider some of their basic properties.
which is not involved in the vanishing of the zeros called “not analytically”. This will be accomplished in next Section. For this purpose we use the Chebyshev polynomials of first and second kind and as preparation we consider some of their basic properties.
Using the following known identity of functions ![]() to Chebyshev polynomials of second kind
to Chebyshev polynomials of second kind ![]() (e.g., [20] [21] [22] [23] [24] and others)
(e.g., [20] [21] [22] [23] [24] and others)
![]() (3.2)
(3.2)
we obtain from (2.4) the following representation of ![]()
![]() (3.3)
(3.3)
It separates from the sum part in (2.4) the function ![]() by using the Chebyshev polynomials of second kind
by using the Chebyshev polynomials of second kind ![]() and this separation is only possible for arbitrary commensurable step-lengths
and this separation is only possible for arbitrary commensurable step-lengths![]() . The Chebyshev polynomials of second kind
. The Chebyshev polynomials of second kind ![]() are essentially the derivatives of Chebyshev polynomials of first kind
are essentially the derivatives of Chebyshev polynomials of first kind ![]() according to
according to
![]() (3.4)
(3.4)
and are related to the Chebyshev ![]() polynomials of first kind
polynomials of first kind ![]() by (among others)
by (among others)
![]() (3.5)
(3.5)
Recurrence relations can be represented, for example, in the following forms (e.g., [21] )
![]() (3.6)
(3.6)
These relations hold for arbitrary complex variable t.
From (3.4) follows with substituted argument
![]() (3.7)
(3.7)
and
![]() (3.8)
(3.8)
where we used in addition to (3.2) the (known) relations
![]() (3.9)
(3.9)
This means that for real variable ![]() the Chebyshev polynomials
the Chebyshev polynomials ![]() and
and ![]() are positive and satisfy the inequalities
are positive and satisfy the inequalities
![]() (3.10)
(3.10)
The Chebyshev polynomials ![]() are mutually orthogonal for real variable x according to
are mutually orthogonal for real variable x according to
![]() (3.11)
(3.11)
For complex variable ![]() they are mutually orthogonal only within the limits of a full period
they are mutually orthogonal only within the limits of a full period ![]() from arbitrary
from arbitrary ![]() up to
up to ![]() according to
according to
![]() (3.12)
(3.12)
that means for basic intervals of lengths ![]() of all trigonometric functions
of all trigonometric functions ![]() and
and ![]() with
with![]() . The analogous relation for the Chebyshev polynomials of second kind is
. The analogous relation for the Chebyshev polynomials of second kind is
![]() (3.13)
(3.13)
The prolongation of these relations to negative ![]() and (or)
and (or) ![]() is possible using the relations given in (3.4) and (3.5).
is possible using the relations given in (3.4) and (3.5).
With (2.4) and (3.3) we have derived different representations of the Xi functions ![]() for step-wise constant Omega functions
for step-wise constant Omega functions ![]() of commensurable step lengths and with sufficiently rapid decrease. We will now analyze their zeros in dependence on the step length
of commensurable step lengths and with sufficiently rapid decrease. We will now analyze their zeros in dependence on the step length![]() . This can be completely done for the principal position of their zeros and is made in the next Section.
. This can be completely done for the principal position of their zeros and is made in the next Section.
4. Two Kinds of Zeros in Commensurable Step-Wise Case
In (3.3) the function ![]() for the commensurable step-wise case which by their vanishing provides the zeros is split in two factors. The first factor
for the commensurable step-wise case which by their vanishing provides the zeros is split in two factors. The first factor ![]() can only vanish on the imaginary axis
can only vanish on the imaginary axis ![]() that means for
that means for ![]() and leads to the zeros
and leads to the zeros
![]() (4.1)
(4.1)
The zeros which all lie on the imaginary axis are equidistant with half of the period length ![]() (see (2.10)). If
(see (2.10)). If ![]() goes to zero then this period length goes from its smallest zero at
goes to zero then this period length goes from its smallest zero at ![]() together with all higher ones to complex infinity3
together with all higher ones to complex infinity3
![]() (4.2)
(4.2)
Thus this kind of zeros vanish in the limiting case of vanishing step length ![]() from the list of zeros and is no more relevant for continuous Omega functions.
from the list of zeros and is no more relevant for continuous Omega functions.
We consider now the second factor in (3.3) more in detail and write it as follows
![]() (4.3)
(4.3)
where we used the identity (3.5) for its transformation. Split in Real and Imaginary part we have
![]() (4.4)
(4.4)
To find the zeros of this expression is the most difficult part of the problem to find all zeros of![]() . First one sees that this part contains the genuine zeros of
. First one sees that this part contains the genuine zeros of ![]() which remain after the limiting transition to vanishing step length
which remain after the limiting transition to vanishing step length![]() . If we diminish the step length
. If we diminish the step length ![]() then, roughly speaking, the differences
then, roughly speaking, the differences ![]() become smaller but in the same measure the number of sum terms enlarges in a certain u-interval
become smaller but in the same measure the number of sum terms enlarges in a certain u-interval ![]() and their products remains nearly constant and also the changes of the polynomial values of
and their products remains nearly constant and also the changes of the polynomial values of ![]() for
for ![]() under fixed variable z go then to zero for continuous Omega functions. From the two conditions for zeros of the expression (4.4) that means the simultaneous vanishing of its Real and Imaginary part
under fixed variable z go then to zero for continuous Omega functions. From the two conditions for zeros of the expression (4.4) that means the simultaneous vanishing of its Real and Imaginary part
![]() (4.5)
(4.5)
it is only simple to establish a manageable condition for zeros on the imaginary axes![]() . In this case the second condition in (4.5) for vanishing of the Imaginary part is identically satisfied and we do not have to be concerned more about this condition. Therefore, for
. In this case the second condition in (4.5) for vanishing of the Imaginary part is identically satisfied and we do not have to be concerned more about this condition. Therefore, for ![]() there remains to be satisfied only the condition of vanishing of the Real part which simplifies in this case to
there remains to be satisfied only the condition of vanishing of the Real part which simplifies in this case to
![]() (4.6)
(4.6)
One may suppose that this condition is solvable at least, in principle, for known Omega functions![]() . In the limiting case of vanishing step length
. In the limiting case of vanishing step length ![]() for continuous Omega functions this provide all “genuine” zeros of
for continuous Omega functions this provide all “genuine” zeros of ![]() on the imaginary axis
on the imaginary axis![]() . These are the zeros which we call zeros of first kind and which are “analytically” since they are gained by vanishing of Real and Imaginary part of an analytic function. There arises the question about possible zeros of
. These are the zeros which we call zeros of first kind and which are “analytically” since they are gained by vanishing of Real and Imaginary part of an analytic function. There arises the question about possible zeros of ![]() for
for ![]() that is off the imaginary axis in commensurable step-wise case and in the case of continuous Omega functions. A simple proof that in case of continuous Omega functions the zeros of
that is off the imaginary axis in commensurable step-wise case and in the case of continuous Omega functions. A simple proof that in case of continuous Omega functions the zeros of ![]() on the imaginary axes are the only ones provides the Second mean-value or Bonnet approach which we give in Section 8. Now, however, we will examine the case of possible zeros in commensurable step-wise case off the imaginary axis.
on the imaginary axes are the only ones provides the Second mean-value or Bonnet approach which we give in Section 8. Now, however, we will examine the case of possible zeros in commensurable step-wise case off the imaginary axis.
We begin now to deal with the problem of zeros of ![]() off the imaginary axis in commensurable step-wise case. First, we derive a modified representation of expression (4.4). The Hyperbolic and Trigonometric functions of real arguments in (4.4) can be again written using the Chebyshev polynomials of first and second kind and according to (3.2) and (3.9) we arrive at the representations
off the imaginary axis in commensurable step-wise case. First, we derive a modified representation of expression (4.4). The Hyperbolic and Trigonometric functions of real arguments in (4.4) can be again written using the Chebyshev polynomials of first and second kind and according to (3.2) and (3.9) we arrive at the representations
![]() (4.7)
(4.7)
with separated Real and Imaginary part. If we exclude the zeros of the factor ![]() which lie on the imaginary axis and are dealt with in (4.4) then for zeros to
which lie on the imaginary axis and are dealt with in (4.4) then for zeros to ![]() off the imaginary axis due to the inequality
off the imaginary axis due to the inequality
![]() (4.8)
(4.8)
we have to satisfy the following two conditions for Real and Imaginary part of (4.7)
![]() (4.9)
(4.9)
The expressions on the two right-hand sides in (4.9) are not the Real and Imaginary part of an analytic function of variable![]() . The zeros which we determine by the two conditions (4.9) are therefore “not analytically” determined. We call them zeros of second kind for the commensurable step-wise kind and discuss them in next Section.
. The zeros which we determine by the two conditions (4.9) are therefore “not analytically” determined. We call them zeros of second kind for the commensurable step-wise kind and discuss them in next Section.
5. Possible Zeros of Xi Function in Commensurable Step-Wise Case off the Imaginary Axis
One case for a possible satisfaction of the second of the conditions (4.9) is immediately to see and is
![]() (5.1)
(5.1)
It leads to the same possible y-values for the zeros as the condition (5.1). For the possible satisfaction of the first of the conditions (4.9) we have to distinguish the cases of even ![]() and odd
and odd ![]() due to
due to
![]() (5.2)
(5.2)
For the Chebyshev polynomials ![]() for argument
for argument ![]() and
and ![]() holds
holds
![]() (5.3)
(5.3)
and inserted in the first condition in (4.9) we get two different forms.
The first condition (4.9) for even ![]() and thus for
and thus for ![]() takes on the form
takes on the form
![]() (5.4)
(5.4)
and for odd ![]() and thus
and thus ![]() we find
we find
![]() (5.5)
(5.5)
The condition (5.4) contains only positive sum terms and cannot vanish. Therefore this case is not possible for zero off the imaginary axis. However, in the case (5.5) we have positive and negative sum terms on the right-hand side and it may or may not become zero for certain![]() . In this case one may have zeros of
. In this case one may have zeros of ![]() off the imaginary axis for the commensurable step-wise case. These zeros go for
off the imaginary axis for the commensurable step-wise case. These zeros go for ![]() to complex infinity as we see from the lowest zero
to complex infinity as we see from the lowest zero ![]() with undetermined
with undetermined ![]() in (5.1).
in (5.1).
Excluding the zeros of ![]() in case of
in case of ![]() there remains now to discuss the last case of simultaneous zeros for variable values
there remains now to discuss the last case of simultaneous zeros for variable values ![]() of the two conditions
of the two conditions
![]() (5.6)
(5.6)
following from (4.9). The right-hand sides of these two conditions are not Real and Imaginary part of an analytic function of the complex variable ![]() and thus it belongs to the case which we call “nonanalytic” ones. It is hardly possible to determine the zeros of the case (5.6) if such exist at all. However, it seems to us that we can prove that also these zeros for
and thus it belongs to the case which we call “nonanalytic” ones. It is hardly possible to determine the zeros of the case (5.6) if such exist at all. However, it seems to us that we can prove that also these zeros for ![]() go to complex infinity. For this purpose, we make in both conditions in (5.6) a Taylor series expansion of the Chebyshev polynomials in powers of
go to complex infinity. For this purpose, we make in both conditions in (5.6) a Taylor series expansion of the Chebyshev polynomials in powers of ![]() according to
according to
![]() (5.7)
(5.7)
For the sum over all ![]() we obtain according to (2.7) in the limiting case
we obtain according to (2.7) in the limiting case ![]()
![]() (5.8)
(5.8)
By combination of (5.7) and (5.8) in the functions of the right-hand side in (5.6) and taking only the first term of the expansions it seems to be evident that the following expressions are true for ![]()
![]() (5.9)
(5.9)
Therefore in the limiting case ![]() the conditions (5.6) cannot be satisfied if (5.9) is correct and there cannot exist zeros
the conditions (5.6) cannot be satisfied if (5.9) is correct and there cannot exist zeros ![]() in considered case4. One may argument in favor of this result also in the following way. If for a certain finite
in considered case4. One may argument in favor of this result also in the following way. If for a certain finite ![]() exists a zero of both conditions (4.9) then in a higher approximation with
exists a zero of both conditions (4.9) then in a higher approximation with ![]() this zero will be destroyed and it may be expected that in the limiting case to vanishing
this zero will be destroyed and it may be expected that in the limiting case to vanishing ![]() it does not stabilize to a certain value.
it does not stabilize to a certain value.
6. Short Summary of the Second Mean-Value Approach to Zeros for Monotonically Decreasing Omega Functions
The approach to the zeros of the Riemann Xi function ![]() and to other functions with a possible integral representation (1.6) with a monotonically decreasing function
and to other functions with a possible integral representation (1.6) with a monotonically decreasing function ![]() which for
which for ![]() vanishes so rapidly that the integral exists was developed in [15] . We compile here the main results which seem to be correct and try to shut the gaps which were for the possible zeros off the imaginary axis.
vanishes so rapidly that the integral exists was developed in [15] . We compile here the main results which seem to be correct and try to shut the gaps which were for the possible zeros off the imaginary axis.
The Second mean-value or Bonnet approach was applied in [15] to the integral (1.6)
![]() (6.1)
(6.1)
We discuss shortly whether the requirements for the application of the Bonnet method are satisfied in our case. The real-valued function ![]() of the real variable u has to be monotonically decreasing (in a wide sense including step-wise cases) that is satisfied for (1.10) and (1.11). The function
of the real variable u has to be monotonically decreasing (in a wide sense including step-wise cases) that is satisfied for (1.10) and (1.11). The function ![]() or its Real and Imaginary part are integrable for fixed finite variable
or its Real and Imaginary part are integrable for fixed finite variable ![]() in the whole complex plane with results which separately for Real and Imaginary part can be taken from (A.1) in Appendix A. For the limiting case
in the whole complex plane with results which separately for Real and Imaginary part can be taken from (A.1) in Appendix A. For the limiting case ![]() we find generalized functions as follows (see Appendix A, (A.7))
we find generalized functions as follows (see Appendix A, (A.7))
![]() (6.2)
(6.2)
Since ![]() is rapidly decreasing for
is rapidly decreasing for ![]() (smaller than an arbitrary Gauss function is sufficient, see also Section 10) this should not be a cause that the Bonnet method cannot be applied. Since in case of convergence the integrand is an analytic function of the variable z the integral (1.6) should also be an analytic function of z and, therefore, also the mean-value function should be such. Thus the application of the Second mean-value or Bonnet approach to the integral (1.6) leads to the following principal form
(smaller than an arbitrary Gauss function is sufficient, see also Section 10) this should not be a cause that the Bonnet method cannot be applied. Since in case of convergence the integrand is an analytic function of the variable z the integral (1.6) should also be an analytic function of z and, therefore, also the mean-value function should be such. Thus the application of the Second mean-value or Bonnet approach to the integral (1.6) leads to the following principal form
![]() (6.3)
(6.3)
with ![]() the mean-value function which usually we do not know exactly and with
the mean-value function which usually we do not know exactly and with
![]() (6.4)
(6.4)
The zeros of the function ![]() lie on the imaginary axis
lie on the imaginary axis ![]() at
at
![]() with
with ![]() and with
and with ![]() excluded. With separated real and imaginary part of all involved functions we have
excluded. With separated real and imaginary part of all involved functions we have
![]() (6.5)
(6.5)
For zeros of the function ![]() it is necessary that the right-hand side vanishes and this is only possible if Real and Imaginary part vanish that is under simultaneous satisfaction of the following two conditions (
it is necessary that the right-hand side vanishes and this is only possible if Real and Imaginary part vanish that is under simultaneous satisfaction of the following two conditions (![]() as zero already excluded)
as zero already excluded)
![]() (6.6)
(6.6)
Clearly, the same condition follows if we calculate the squared modulus of (6.5) and set it equal to zero
![]() (6.7)
(6.7)
which is only possible if both squares on the right-hand side vanish that leads again to the two conditions (6.6) for zeros.
From the first condition (6.6) follows for zeros ![]()
![]() (6.8)
(6.8)
as one equivalent to it and suggests how difficult it would be to find such values ![]() that they also satisfy the second condition in (6.6) for a certain k. We now discuss how this simplifies for the imaginary axis
that they also satisfy the second condition in (6.6) for a certain k. We now discuss how this simplifies for the imaginary axis ![]() where due to
where due to ![]() the first condition in (6.6) is identically satisfied.
the first condition in (6.6) is identically satisfied.
From the symmetry (1.6) of the Xi function ![]() follows for the function
follows for the function ![]()
![]() (6.9)
(6.9)
and as consequence separated for its Real and Imaginary part
![]() (6.10)
(6.10)
From (6.10) follows then for the imaginary axis ![]() the vanishing of
the vanishing of ![]() due to
due to ![]() and the function (6.5) possesses the simple form
and the function (6.5) possesses the simple form
![]() (6.11)
(6.11)
For the zeros on the imaginary axis follows now from the vanishing of ![]() the only condition (see (6.6))
the only condition (see (6.6))
![]() (6.12)
(6.12)
with the solutions (![]() was already excluded before)
was already excluded before)
![]() (6.13)
(6.13)
However, we do not explicitly know the function ![]() and also in case we would know it, in general, we were not able to solve it and to determine all solutions. For the proof of the Riemann hypothesis and other possible cases for appropriate Omega functions
and also in case we would know it, in general, we were not able to solve it and to determine all solutions. For the proof of the Riemann hypothesis and other possible cases for appropriate Omega functions ![]() this is not necessary. We have only to ensure that the solutions (6.13) provide all solutions for the zeros of Xi functions
this is not necessary. We have only to ensure that the solutions (6.13) provide all solutions for the zeros of Xi functions ![]() to the Omega function
to the Omega function ![]() in (1.10) and other appropriate functions such as (1.11) that is the case for continuous Omega functions. This and some technical approaches we investigate in the next two Sections.
in (1.10) and other appropriate functions such as (1.11) that is the case for continuous Omega functions. This and some technical approaches we investigate in the next two Sections.
7. Further Development of the Second Mean-Value Approach to Zeros of Monotonically Decreasing Omega Functions
We begin now to investigate the restrictions for zeros (6.6) in the Second mean-value approach by derivation of some more technical relations which provide the extension of the functions in this approach from the imaginary axis ![]() to the whole complex z-plane.
to the whole complex z-plane.
In [15] was derived that an analytic function
![]() (7.1)
(7.1)
with Real part ![]() and Imaginary part
and Imaginary part ![]() on the imaginary axis possesses the following operational identities that means can be applied to arbitrary functions
on the imaginary axis possesses the following operational identities that means can be applied to arbitrary functions ![]() 5
5
![]() (7.2)
(7.2)
This is a consequence of the Cauchy-Riemann equations. Applied to the function ![]() this provides
this provides
![]() (7.3)
(7.3)
They can be derived by integration of the Cauchy-Riemann equations for analytic functions and allow to determine the functions ![]() and
and ![]() if their values
if their values ![]() and
and ![]() on the imaginary axis are known. These equations simplify further if the function
on the imaginary axis are known. These equations simplify further if the function ![]() is vanishing and are then
is vanishing and are then
![]() (7.4)
(7.4)
In this form they may be applied to the considered problem.
Due to vanishing of ![]() on the y-axis according to (6.11) for the function
on the y-axis according to (6.11) for the function ![]() to the Xi function
to the Xi function ![]() we may directly apply relations (7.4) in the form
we may directly apply relations (7.4) in the form
![]() (7.5)
(7.5)
However, we may apply them also to the function ![]() with
with ![]() on the imaginary axis and they take on in this case the following form for the Imaginary part of
on the imaginary axis and they take on in this case the following form for the Imaginary part of ![]()
![]() (7.6)
(7.6)
and for the Real part of ![]()
![]() (7.7)
(7.7)
One sign in the operator identities on the right-hand side of (7.6) and (7.7) has changed in comparison to (7.4). This happened since ![]() is now the Imaginary part of
is now the Imaginary part of ![]() which alone is non-vanishing on the imaginary axis and from (7.3) follows for the reconstruction in this case
which alone is non-vanishing on the imaginary axis and from (7.3) follows for the reconstruction in this case
![]() (7.8)
(7.8)
The equivalence of the two forms (7.5) and (7.6) to (7.4) can be also established by the following general identities in application of the operators ![]() and
and ![]() to a product
to a product ![]() of two functions
of two functions ![]() and
and ![]()
![]() (7.9)
(7.9)
and in similar way
![]() (7.10)
(7.10)
In their structure we find a striking similarity to the addition theorems for Cosine and Sine functions. Their derivation becomes simple if in intermediate calculations
we make the transition to the complex displacement operators ![]() that
that
we do not write down. We emphasize only that the braces ![]() in (7.9) and (7.10) are understood in the sense that the operators inside do not exceed their action outside their brace limits.
in (7.9) and (7.10) are understood in the sense that the operators inside do not exceed their action outside their brace limits.
If we apply (7.9) and (7.10) to eigenfunctions ![]() and
and ![]() of the operator Hermitean operator
of the operator Hermitean operator ![]() then from (7.9) follows
then from (7.9) follows
![]() (7.11)
(7.11)
and analogously
![]() (7.12)
(7.12)
This may be considered as alternative proof of the relations (7.9) and (7.10) which play a role for the transition from the imaginary axis to axes parallel to the imaginary axis. In the following the eigenvalues and eigenfunctions of the operator
![]() play a main role.
play a main role.
8. Principal Position of Analytic Zeros of Xi Functions in the Second Mean-Value Approach Including the Riemann Hypothesis
As two independent conditions for zeros of the function (6.5) in considered case of monotonically decreasing Omega functions including step-wise constant Omega functions with incommensurable step lengths we derived (6.6) using (7.6) and (7.7). The result may be written
![]() (8.1)
(8.1)
We now introduce the abbreviation
![]() (8.2)
(8.2)
and may write then the conditions (1) shorter
![]() (8.3)
(8.3)
Since usually we do not know this function explicitly we will make a general expansion of ![]() into a complete orthogonal set of eigenfunctions of the
into a complete orthogonal set of eigenfunctions of the
operator ![]() to real eigenvalues p which are
to real eigenvalues p which are
![]() (8.4)
(8.4)
The given orthonormality using the delta “function” is well known. The expansion
of ![]() into the complete set of eigenfunctions
into the complete set of eigenfunctions ![]() of the operator
of the operator ![]()
is nothing else than the Fourier integral
![]() (8.5)
(8.5)
With this general assumption we now go into the conditions for zeros (8.1).
Inserting (8.5) into the two conditions (8.3) they take on the form
![]() (8.6)
(8.6)
Due to orthonormality of the eigenfunctions in the Fourier expansion from these two equations follows
![]() (8.7)
(8.7)
and we have to solve these two equations for the Fourier components ![]() from which the last is an inhomogeneous equation. The general solution of this infinite linear system with x as parameter is the general solution of the homogeneous equations plus special solutions of the inhomogeneous equation.
from which the last is an inhomogeneous equation. The general solution of this infinite linear system with x as parameter is the general solution of the homogeneous equations plus special solutions of the inhomogeneous equation.
The homogeneous equations to (8.7) are
![]() (8.8)
(8.8)
Solutions for ![]() may only exist at such values of the variable x for which
may only exist at such values of the variable x for which ![]() and
and ![]() that means
that means ![]() and
and ![]() have to vanish simultaneously and since at these points we have simple zeros of the mentioned functions the general solutions of the two Equation (8.8) are6
have to vanish simultaneously and since at these points we have simple zeros of the mentioned functions the general solutions of the two Equation (8.8) are6
![]() (8.9)
(8.9)
with constants ![]() and
and ![]() and where we took into account the symmetry of Real and Imaginary part of the Xi function. These two solutions are contradictory and exclude themselves mutually. The only way out of this dilemma is to assume
and where we took into account the symmetry of Real and Imaginary part of the Xi function. These two solutions are contradictory and exclude themselves mutually. The only way out of this dilemma is to assume
![]() (8.10)
(8.10)
meaning that there does not exist a common solution of the two homogeneous equations for finite variable x and therefore zeros for ![]() off the imaginary axis. From the inhomogeneous Equation (8.7) inserting
off the imaginary axis. From the inhomogeneous Equation (8.7) inserting ![]() follows then as general solution for zeros for the Fourier components
follows then as general solution for zeros for the Fourier components ![]()
![]() (8.11)
(8.11)
and after inverse Fourier transformation according to (8.5) with the abbreviation
![]() (8.12)
(8.12)
This is our already known equation for zeros of the Xi function ![]() on the imaginary axis
on the imaginary axis![]() .
.
We excluded in this way all “analytical” zeros off the imaginary axis in limiting case of continuous Omega functions. Furthermore, for the limiting transition from the commensurable step-wise case all zeros off the imaginary axis go to complex infinity for step length ![]() or do not provide any solution. Since to the included cases of Omega functions belongs also the Omega function to the Riemann Xi function
or do not provide any solution. Since to the included cases of Omega functions belongs also the Omega function to the Riemann Xi function ![]() it seems to be a proof of the Riemann hypothesis that all zeros of the Riemann Xi function lie on the imaginary axis and thus also all nontrivial zeros of the Riemann zeta function
it seems to be a proof of the Riemann hypothesis that all zeros of the Riemann Xi function lie on the imaginary axis and thus also all nontrivial zeros of the Riemann zeta function![]() . For the modified Bessel functions mentioned in Section 1 for which this property is already proved by their differential equations (e.g., [25] [26] ) this would be an alternative proof. We think that the commensurable step-wise cases within all cases of monotonically decreasing Omega functions play a similar role as the rational numbers within all real numbers.
. For the modified Bessel functions mentioned in Section 1 for which this property is already proved by their differential equations (e.g., [25] [26] ) this would be an alternative proof. We think that the commensurable step-wise cases within all cases of monotonically decreasing Omega functions play a similar role as the rational numbers within all real numbers.
9. Some Further Remarks to the Derivations According to the Bonnet Approach
One may be astonished and it was an essential problem that in the Second mean-value approach we found according to (8.10) that all zeros lie on the imaginary axis whereas in the commensurable step-lengths approach we obtained also zeros off the imaginary axis. We could, however, show that for vanishing step lengths ![]() the additional zeros off the imaginary axis go to complex infinity. For this purpose we followed the derivation of Second mean-value (Bonnet) approach in the cited monographs [16] [17] [18] and could not discover a defect in their correctness also for the case of the commensurable step-wise approach. They are derived in mentioned sources for real mean vales. We extended it to the complex analytic mean-value function
the additional zeros off the imaginary axis go to complex infinity. For this purpose we followed the derivation of Second mean-value (Bonnet) approach in the cited monographs [16] [17] [18] and could not discover a defect in their correctness also for the case of the commensurable step-wise approach. They are derived in mentioned sources for real mean vales. We extended it to the complex analytic mean-value function ![]() that is apparently justified for the whole complex integral (1.6) for continuous Omega functions but only not for the commensurable step-wise case where we could separate a factor
that is apparently justified for the whole complex integral (1.6) for continuous Omega functions but only not for the commensurable step-wise case where we could separate a factor ![]() (see (3.3)) with its own zeros which are moreover periodically on the imaginary axis and the remaining functions with real and imaginary part cannot be unified to an analytic function. In this case as it seems to us one has to introduce two different mean-value function
(see (3.3)) with its own zeros which are moreover periodically on the imaginary axis and the remaining functions with real and imaginary part cannot be unified to an analytic function. In this case as it seems to us one has to introduce two different mean-value function ![]() and
and ![]() separately instead of one analytic mean-value function
separately instead of one analytic mean-value function![]() . These functions which are then involved into real and imaginary part can be calculated according to (A.1) in the following way
. These functions which are then involved into real and imaginary part can be calculated according to (A.1) in the following way
![]() (9.1)
(9.1)
We did not investigate this up to now.
What was incorrect or even wrong in our article [15] ! We obtained only the
“analytic” zeros which are involved in ![]() and, principally, lie on the
and, principally, lie on the
imaginary axis![]() . Moreover, this was not shown in such evident way as it is made in present paper in Section 8 by derivation of the contradiction (8.9) for the homogeneous solutions for the Fourier components of the function in the Hyperbolic Sine. The “non-analytic” solutions which are possible in the commensurable step-wise case (and, apparently, are possible only in this case as the limiting case
. Moreover, this was not shown in such evident way as it is made in present paper in Section 8 by derivation of the contradiction (8.9) for the homogeneous solutions for the Fourier components of the function in the Hyperbolic Sine. The “non-analytic” solutions which are possible in the commensurable step-wise case (and, apparently, are possible only in this case as the limiting case ![]() suggests) were not seen since they are not contained in
suggests) were not seen since they are not contained in
the function (6.3). The operator identity ![]() which
which
was applied there to the mean-value function was a faux pas and may be only used for identical transformations and simplifications but cannot provide new conclusions for the position of the zeros. However, using it one may see that the homogeneous equations to (8.6) or (8.7) are contradictory without providing a solution for![]() . Our paper [19] was not intended as approach to a proof of the Riemann hypothesis and similar theorems for the modified Bessel function and was merely intended as illustration what one may expect for the zeros going from lower to higher approximations in Taylor series expansion of the Xi function but it was there shortly sketched the idea that one may establish for the commensurable step-wise case the exclusion of all additional zeros (now called “non-analytic” ones) off the imaginary axis and which go to complex infinity in the limiting case of vanishing step length. The execution of this plan in present paper proved to be much more difficult and branched than thought at this time.
. Our paper [19] was not intended as approach to a proof of the Riemann hypothesis and similar theorems for the modified Bessel function and was merely intended as illustration what one may expect for the zeros going from lower to higher approximations in Taylor series expansion of the Xi function but it was there shortly sketched the idea that one may establish for the commensurable step-wise case the exclusion of all additional zeros (now called “non-analytic” ones) off the imaginary axis and which go to complex infinity in the limiting case of vanishing step length. The execution of this plan in present paper proved to be much more difficult and branched than thought at this time.
10. Monotonic Decrease of Omega Function as Sufficient (or Necessary (or Both)) Condition for Zeros of Xi Functions Only on the Imaginary Axis
The monotonic decrease of the Omega function ![]() in the integral
in the integral
![]() (10.1)
(10.1)
is a necessary condition for the applicability of the Second mean-value approach of integration (Bonnet method) but it is not necessary for more general Xi functions ![]() which may possess zeros only on the imaginary axis
which may possess zeros only on the imaginary axis![]() . This becomes already evident since by multiple partial integration the integral (10.1) under smoothness conditions of
. This becomes already evident since by multiple partial integration the integral (10.1) under smoothness conditions of ![]() at
at ![]() can be transformed to
can be transformed to
![]() (10.2)
(10.2)
where already ![]() is not monotonically decreasing (or increasing) and
is not monotonically decreasing (or increasing) and ![]() is not even definite.
is not even definite.
We consider now two simple examples of Omega functions which are not monotonically decreasing but lead to a Xi function with zeros only on the imaginary axis. The first example is (Figure 2(a))
![]() (10.3)
(10.3)
It is known that the modified analytic Bessel function ![]() possesses zeros only on the imaginary axis and for the factor
possesses zeros only on the imaginary axis and for the factor ![]() this is evident. The second example is (Figure 2(a))
this is evident. The second example is (Figure 2(a))
![]() (10.4)
(10.4)
with![]() . We see that also in this case the Xi function possesses
. We see that also in this case the Xi function possesses
zeros only on the imaginary axis. In addition, we see that the zeros of the second factor are not simple zeros but possess the multiplicity 2 (double zeros). These two cases are not comprised by the Second mean-value approach to the integral (10.1) and already ![]() which is needed in this approach (6.3) is in these two cases vanishing
which is needed in this approach (6.3) is in these two cases vanishing![]() .
.
![]() (a)
(a) ![]() (b)
(b)
Figure 2. Four Omega functions to the explanation of properties of Xi functions ((a) and (b)). In the first two examples the Omega functions (![]() Heaviside step function) are not monotonically decreasing to zero but, nevertheless, the corresponding Xi functions possess zeros only on the imaginary axis. We know from the transition (1.6) to a representation by the derivative of the Omega function that this must hold also under certain condition if the Omega function consist of two parts, a monotonically increasing and a monotonically decreasing part. In the two other examples the Omega functions are not decreasing faster than exponentially and the integral for the Xi function is not convergent in the whole z-plane. The Xi functions possess then poles in these cases.
Heaviside step function) are not monotonically decreasing to zero but, nevertheless, the corresponding Xi functions possess zeros only on the imaginary axis. We know from the transition (1.6) to a representation by the derivative of the Omega function that this must hold also under certain condition if the Omega function consist of two parts, a monotonically increasing and a monotonically decreasing part. In the two other examples the Omega functions are not decreasing faster than exponentially and the integral for the Xi function is not convergent in the whole z-plane. The Xi functions possess then poles in these cases.
The considerations show that monotonic decreasing of the Omega function does not belong to the necessary conditions for the absence of zeros in the Xi functions off the imaginary axis. However, it is a sufficient criterium for zeros only on the imaginary axis due to the applicability of the Second mean-value approach in this case to the integral (10.1), where the step-wise constant Omega functions with commensurable step length have to be excluded that means a set of measure zero within the whole set of possible Omega functions.
The Omega function in (10.1) has to vanish in infinity so rapidly that the integral exists. If the convergence is only guaranteed for a part of the z-plane as
it is the case for decrease such as functions ![]() with positive fixed a then
with positive fixed a then
appear also poles in the Xi function as the following two examples show, first (Figure 2(b))
![]() (10.5)
(10.5)
with two simple poles on the real axis at ![]() and
and ![]() but without zeros, and second (Figure 2(b))
but without zeros, and second (Figure 2(b))
![]() (10.6)
(10.6)
with an infinite series of simple poles on the real axis at
![]() (the lowest two agree with that of (10.5)) but also
(the lowest two agree with that of (10.5)) but also
without zeros at all. In the last two cases the integral (10.1) does not converge in the whole z-plane.
We mention here in addition the instructive example of linear decrease of the Omega function ![]() up to
up to ![]() for a finite value
for a finite value ![]()
![]() (10.7)
(10.7)
It leads to zeros only on the imaginary axis at![]() .
.
However, these zeros are double zeros, the same as for the second factor in (10.4)). This example shows that not in all cases for monotonically decreasing Omega functions one obtains Xi functions with only simple zeros on the imaginary axis. Considered for the whole real axis ![]() this is not a strictly monotonically decreasing Omega function.
this is not a strictly monotonically decreasing Omega function.
11. Conclusions
Two functions plaid in our derivations the main role: the Xi function ![]() of the complex variable z and the Omega function
of the complex variable z and the Omega function ![]() of the real variable u which are connected by the integral in (1.6). The Omega function is supposed to be a monotonically (non-strictly) decreasing function up to zero in infinity for
of the real variable u which are connected by the integral in (1.6). The Omega function is supposed to be a monotonically (non-strictly) decreasing function up to zero in infinity for ![]() and it is stated that the Xi function possesses zeros only on the imaginary axis y if the Omega function is not a step-wise constant function with commensurable step lengths. The step-wise constant Omega functions with commensurable step lengths are taken as approximations of the considered Xi function with final limiting procedure of step length
and it is stated that the Xi function possesses zeros only on the imaginary axis y if the Omega function is not a step-wise constant function with commensurable step lengths. The step-wise constant Omega functions with commensurable step lengths are taken as approximations of the considered Xi function with final limiting procedure of step length ![]() going to zero where the zeros which do not lie on the imaginary axis and a part of additional zeros on the imaginary axis go to complex infinity. We show that due to splitting of their Xi function into the product (3.3) they possess two different kinds of zeros where the zeros of first factor are not restricted to the imaginary axis but go to complex infinity in the limiting case of vanishing step lengths whereas the zeros of the second factor stabilize to the “genuine” zeros of the considered function and are restricted to the imaginary axis. Since the made assumptions are true for the Omega function to the Riemann Xi function this proves if correct also the Riemann hypothesis that all non-trivial zeros of the Riemann zeta function lie on
going to zero where the zeros which do not lie on the imaginary axis and a part of additional zeros on the imaginary axis go to complex infinity. We show that due to splitting of their Xi function into the product (3.3) they possess two different kinds of zeros where the zeros of first factor are not restricted to the imaginary axis but go to complex infinity in the limiting case of vanishing step lengths whereas the zeros of the second factor stabilize to the “genuine” zeros of the considered function and are restricted to the imaginary axis. Since the made assumptions are true for the Omega function to the Riemann Xi function this proves if correct also the Riemann hypothesis that all non-trivial zeros of the Riemann zeta function lie on
the axis parallel to the imaginary axis with real part![]() . This is accomplished in
. This is accomplished in
Section 8 by an, apparently simple, proof. Our approach is very similar to the primary introduction of the notion of a definite integral of a function by making first a step-wise approximation of the function and then going to zero with the step lengths by a limiting procedure.
The further considerations of this article (Sections 6 - 8) show that the treatment by the Second mean-value theorem is an alternative one to other approaches. To exclude the cases of Xi functions with zeros off the imaginary axis was absent in our article [15] and is here made. In Section 10, it is clarified which role plays the condition of monotonic decrease of the Omega function with the result that it is sufficient for presence of zeros only on the imaginary axis (under the other made assumptions) but is not necessary for this. We give examples with not monotonically decreasing Omega functions which lead to Xi functions with zeros only on the imaginary axis. In our examples these zeros are not simple zeros in all cases. In case of Omega functions which decrease in infinity only as simple exponential function (exponent proportional only to variable u) the integral (1.6) is no more convergent in the whole complex z-plane and there appear poles in the Xi function.
It seems to us that also an approach from the zeros of Taylor series approximations of the Xi function should be possible in case if it is perfectly possible to prove that in the transition to next higher approximations all zeros off the imaginary axis go to complex infinity and only the zeros on the imaginary axis stabilize as the “genuine” zeros of the Xi functions to continuous Omega functions with the supposed properties. The considered illustrations in [19] show such a behavior but a difficulty of the analytic treatment in this way is here that the transition from an approximation to the next higher approximation is hardly possible in perfect analytic form without further approximations leading finally to quadratic equations which are then easily to solve.
Acknowledgements
For hints I express my gratitude to Victor Katsnelson and J. Gélinas. Great thanks go also to my son Arne (economist) in all papers for help with computers, computer programs and sometimes with simple remarks und questions.
Appendix A
A category of proper and improper integrals over products of Hyperbolic and Trigonometric functions
For the separate application of the second mean-value approach (Bonnet approach) to Real- and Imaginary part of (1.7) we derive here some proper and corresponding improper integrals where the last lead to Generalized functions.
The first two (proper) integrals with real parameter a which we need for the Bonnet approach are known with the result
![]() (A.1)
(A.1)
For a possible approach of the Bonnet approach to the lower representation in (1.7) separately to the increasing and decreasing part (not made in this article) we give the following two analogous integrals
![]() (A.2)
(A.2)
We calculate now the corresponding improper integrals for ![]() and start from the following two integrals which are well known from the theory of Fourier transformation of Generalized functions (e.g., [27] , chap. II, §5, (15), (15’) and §9, (31), (31’), and from many others)
and start from the following two integrals which are well known from the theory of Fourier transformation of Generalized functions (e.g., [27] , chap. II, §5, (15), (15’) and §9, (31), (31’), and from many others)
![]() (A.3)
(A.3)
where ![]() applied to a function means that the principal value is to take at the singularity of the kind of a simple pole. As a consequence of these relations follows
applied to a function means that the principal value is to take at the singularity of the kind of a simple pole. As a consequence of these relations follows
![]() (A.4)
(A.4)
From this follows by changing the order of differentiation and integration
![]()
![]() (A.5)
(A.5)
Using Taylor series expansions of the Hyperbolic functions we generalize this now to a category of improper integrals from which the first is calculated more in detail as follows
![]() (A.6)
(A.6)
Together with further such improper integrals calculated in analogous way this provides
![]() (A.7)
(A.7)
We emphasize that such generalized functions as ![]() and
and ![]() do
do
not belong to the mostly considered spaces of Generalized function ![]() or
or ![]() but to the space
but to the space ![]() of Fourier transformations of functions of
of Fourier transformations of functions of ![]() over the space
over the space ![]() of Fourier transforms of basic functions of
of Fourier transforms of basic functions of ![]() and, clearly here, of two variables
and, clearly here, of two variables ![]() with the possibility to extend the range of definition of the variables to complex ones.
with the possibility to extend the range of definition of the variables to complex ones.
NOTES
1Our first and main source for detailed serious studies in this field was the book of Edwards [2] after knowing the problem much earlier mainly from popular articles and books to recreation mathematics.
2To this case belong also functions with only rational proportions of step-length (that means commensurable step lengths) for which then the smallest common part of all step lengths can be taken as (genuine) step length u0.
3Clearly, there exists only one complex infinity.
4In principle, it is already sufficient that the first of these conditions is satisfied.
5The analogous form was given for known functions ![]() and
and ![]() on the x-axis which, however, is not needed here for our further investigations.
on the x-axis which, however, is not needed here for our further investigations.
6Due to ![]() no derivatives of the delta function with
no derivatives of the delta function with ![]() can be present in the solutions.
can be present in the solutions.