1. Introduction
Vertical infiltration is a common physical phenomenon of water movement in porous media which is of great interest in many earth and plant sciences. Vertical soil-water flow plays an important role in understanding the phenomena of runoff, groundwater recharge, and transport of contaminants. Especially in the vadose zone, the soil moisture strongly influences the plants’ growing process. Historically, Buckingham [1] presented two basic ideas in the development of soil water movement concerning the vadose zone: the capillary potential and the capillary conductivity. Later, Gardner and Widsoe [2] and Richards [3] introduced the diffusion phenomenon in the concept of soil-water movement, which was completed later by Childs [4] [5]. The equation of flow arising from Darcy’s or Darcy-Buckingham equation and the law of conservation of mass is, after Klute [6]:
(1)
where θ = the moisture content (cm3/cm3), K = the unsaturated hydraulic conductivity (cm/s) and Φ = the total potential (cm):
(2)
In Equation (2), Ψ = the pressure potential or capillary potential (cm) and z = the gravitational component (cm) and we adopt that z is taken positive downward. Introducing Equation (2) in (1) provides:
(3)
By introducing the diffusivity D (cm2/s):
(4)
Equation (3) becomes:
(5)
and in the vertical dimension z:
(6)
The initial and boundary conditions are:
(7)
For
, Equation (6) with initial and boundaries conditions (7) describes the vertical infiltration of water if a constant moisture content at z = 0 is applied, as initially described by Philip [7].
Analytical solutions of the one-dimensional Equation (6) are available under several simplifications. Philip [7] has obtained a semi-analytical solution of Equation (6) by introducing a Boltzman transformation. His solution was presented as a power series in t1/2. Parlange [8] transformed Equation (6) and considered the
first integral
of the transformed equation negligible compared to the
other terms. Subsequently, he developed an iterative method to solve the remainder equation. Philip [9] has introduced a linearization technique for the solution of the above non-linear infiltration problem. He explained that the solutions of the linearized equation do not give accurate detailed description of the phenomenon. However, the linear equation yields useful estimates of integral properties of cumulative infiltration I and infiltration rate v0. In general, exact nonlinear solutions are derived for specific forms of the soil-water relationship [10] [11] [12] [13] [14]. Richards’s equation is also linearized by considering exponential form of the hydraulic conductivity and the moisture content vs. the pressure head [14] [15]. Approximate solutions are also derived using the form of Brooks and Corey of hydraulic conductivity and the moisture content vs. the pressure head and considering a rectangular profile of moisture content [16] [17] [18]. Su et al. [19], solved the equation of Richards, using a new method based on the Principle of Least Action and the Variational Principle.
The numerical methods—finite difference and finite element—presented in [20] - [33] overcome most of the limitations to result to analytical solutions.
The calculation of water flow in the unsaturated zone requires the knowledge of the initial and boundary conditions as well as of the various soil parameters. Until today, these conditions and parameters were assumed well-defined, and this assumption is based principally in measurements. But they are subject to different kinds of uncertainty, due to human and machine imprecision. In many cases the uncertainties were considered in statistical terms as random variables with given mean values, variances and correlations. But these methods require the exact knowledge of mean values, variances and correlations, and often suffer from insufficient amount of accurate measurement data. For example, the accuracy of the linear distance between two points depends upon the precision of the location of the reference points. The precision rarely being perfect, dimensional limits would be imposed, often of the bilinear type
. This bilinear type set was assumed random and the probability theory was accepted valid. But randomness is an ideal tool only where a sufficiently long series of independent random experiments is available. In the cases where we have a small set of measurements, fuzzy set theory is ideal for formalizing incomplete information expressed in terms of fuzzy propositions with inherent vagueness. The same principle could clearly be extended to other applications, including non-geometric cases, such as chemical composition, machine registrations etc.
Today the fuzzy set theory provides methods for introducing imprecise information in a possibilistic sense. Zadeh [34] initially introduced the fuzzy set theory for facing imprecision or vagueness and since then this theory has been applied in various fields of science. In the present work, the solution of a linear one-dimensional vertical infiltration equation with fuzzy initial and boundary conditions is presented. This equation is a parabolic partial differential equation, describing the vertical water movement in a porous medium. The problem of fuzzy differential equations is related to mathematical modelling and engineering applications. Initially differentiable fuzzy functions were studied by Puri and Ralescu [35], who generalized and extended the concept of Hukuhara differentiability of set valued mappings to the class of fuzzy mappings (H-derivative, Hukuhara, [36]). Also, Kaleva [37] and Seikkala [38] developed a theory for fuzzy differential equations. Many related works have been carried out in theoretical and applied topics for fuzzy differential equations with H-derivative [37] [38] [39] [40]. But in some cases, this method suffers certain disadvantages that lead to solutions with increasing support as time t increases [41] [42]. This proves that in some cases the H-derivative solution is not a good generalization of the corresponding crisp case. Bede and Gal [43] mention: “This approach has the disadvantage that it leads to solutions with increasing support, fact which is solved by interpreting a fuzzy differential equation as a system of differential inclusions. But this last-mentioned approach has at its turn some shortcomings. The main shortcoming is that one cannot talk about the derivative of a fuzzy-number-valued function, since a fuzzy differential equation is directly interpreted with the help of differential inclusions without having a derivative”. In order to overcome the above deficiency, the generalized Hukuhara differentiability (gH-differentiability) was introduced by Bede and Gal [44] and Stefanini and Bede [45]. In that case, the solution exists under much less restrictive conditions, but it does not always exist. Recently the general differentiability (g-differentiability) concept is proposed, which further extends the gH-differentiability (Bede and Stefanini [46], Stefanini and Bede [47]). This new derivative is defined for a larger class of fuzzy functions than the Hukuhara derivative. Allahviranloo et al. [48] introduced the (gH-p) differentiability for partial derivatives as an extension of the above theory.
In this paper, as is stated above, the case of linear vertical infiltration is studied, with imprecise boundaries conditions. The diffusivity is considered constant and the crisp problem is solved using the Laplace transform. For the fuzzy solution, the crisp solution is introduced first and then the problem is fuzzified. Then the problem is solved according to the theories presented in [49] [50], and a fuzzy solution is presented. Consequently, the first derivatives with respect to t and z, as well as the second derivative with respect to z of the problem are examined. The article is organized as follows: in the Materials and Methods section, the physical problem is presented, and the Fuzzy model is applied to it. The mathematical model is formulated, using certain characteristics with fuzzy derivatives, and it is analyzed in its fuzzy form. In the Results and Discussion section, the model is applied in sample soil data, resulting to the fuzzy moisture, the fuzzy cumulative infiltration as well as the fuzzy infiltration rate versus time. The significance and the main advantage of this study, is the introduction of fuzzy logic to solve the problem of vertical infiltration, which is a problem involving partial differential equations and it presents uncertainties in its input variables.
2. Materials and Methods
2.1. The Physical Problem of One-Dimensional Linear Vertical Infiltration in Its Crisp Form
Equation (6) mentioned in the introduction, is called infiltration equation by Philip [51], because it describes the vertical water flow in a porous medium. For
, the above equation with initial and boundary conditions provided by Equation (7), describes the vertical infiltration of water by applying a constant moisture content at z = 0.
In the above equation, Philip [9] has estimated the diffusivity as follows:
, (8)
where S is the sorptivity [LT-1/2]. The linearized form of Equation (6) thus becomes:
, (9)
with the same initial and boundary conditions:
(10)
By writing the term
in the following form:
, (11)
he has considered that k is constant by matching linear and non-linear values of infiltration rate (
) and has obtained the value:
(12)
In Equation (12), Ks = the hydraulic conductivity at saturation, Kr = the residual hydraulic conductivity, θs = the moisture content at saturation, and θr = the residual moisture content. He now poses in Equation (9):
(13)
and Equation (9) becomes:
(14)
with initial and boundaries conditions:
(15)
The solution of this equation is ( [50]):
(16)
The cumulative infiltration is:
(17)
while the infiltration rate is:
. (18)
2.2. Generalities of the Fuzzy Model
Note: In order to facilitate the readers non-familiar with the fuzzy theory, we describe here some definitions concerning preliminaries of fuzzy theory and some definitions about the differentiability.
2.2.1. Definition 1. Membership Function
A fuzzy set
on a universe set X is a mapping
, assigning to each element
a degree of membership
. The membership function is also defined as
with the properties:
1)
is upper semi continuous, 2)
, outside of some interval
, 3) there are real numbers
, such that
is increasing on
, decreasing on
and
for each
, 4)
is a convex fuzzy set (i.e.
.
2.2.2. Definition 2. Closure
Let X be a Banach space and
be a fuzzy set on X. We define the a-cuts of
as
, and for
, we define the closure
.
2.2.3. Definition 3. Space of All Compact and Convex Sets
Let Ҡ(X) the family of all nonempty compact convex subsets of a Banach space. A fuzzy set
on X is called compact if
Ҡ(X),
. The space of all compact and convex fuzzy sets on X is denoted as Ƒ(X).
2.2.4. Definition 4. α-Cut Forms
Let
. The α-cuts of
, are:
. According to representation theorem of Negoita and Ralescu [39] and the theorem of Goetschel and Voxman [52], the membership function and the α-cut form of a fuzzy number
, are equivalent and in particular the α-cuts 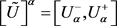 uniquely represent
uniquely represent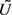 , provided that the two functions are monotonic (
, provided that the two functions are monotonic (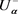 increasing,
increasing, 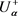 decreasing) and
decreasing) and  for
for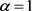 .
.
2.2.5. Definition 5. gH-Differentiability (Bede and Stefanini, [46])
Let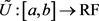 , be such that
, be such that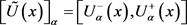 . Suppose that the functions
. Suppose that the functions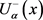 ,
, 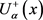 are real-valued functions, differentiable with respect to x, uniform with respect to
are real-valued functions, differentiable with respect to x, uniform with respect to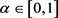 . Then the function
. Then the function 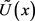 is gH-differentiable at a fixed
is gH-differentiable at a fixed 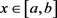 if and only if one of the following two cases holds:
if and only if one of the following two cases holds:
1) 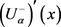 is increasing,
is increasing, 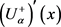 is decreasing as functions of α, and
is decreasing as functions of α, and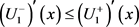 , or 2)
, or 2) 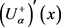 is increasing,
is increasing, 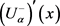 is decreasing as functions of α, and
is decreasing as functions of α, and![]() .
.
Note:![]() . In both cases above, the
. In both cases above, the ![]() derivative is a fuzzy number.
derivative is a fuzzy number.
2.2.6. Definition 6. gH-Differentiability at x0
Let ![]() and
and ![]() with
with![]() ,
, ![]() both differentiable at x0. We say that (Bede and Stefanini, [46]):
both differentiable at x0. We say that (Bede and Stefanini, [46]):
· ![]() is (i)-gH-differentiable at x0 if (i)
is (i)-gH-differentiable at x0 if (i) ![]()
· ![]() is (ii)-gH-differentiable at x0 if (ii)
is (ii)-gH-differentiable at x0 if (ii) ![]()
2.2.7. Definition 7. g-Differentiability
Let ![]() be such that
be such that![]() . If
. If ![]() and
and ![]() are differentiable real-valued functions with respect to x, uniform for
are differentiable real-valued functions with respect to x, uniform for![]() , then
, then ![]() is g-differentiable and we have [46]:
is g-differentiable and we have [46]:
![]() ,
,
2.2.8. Definition 8. Implication of g-Differentiability
The gH-differentiability implies g-differentiability, but the inverse is not true.
2.2.9. Definition 9. [gH-p] Differentiability
A fuzzy-valued function ![]() of two variables is a rule that assigns to each ordered pair of real numbers (x, t) in a set D, a unique fuzzy number denoted by
of two variables is a rule that assigns to each ordered pair of real numbers (x, t) in a set D, a unique fuzzy number denoted by![]() . Let
. Let![]() ,
, ![]() and
and![]() ,
, ![]() are real valued functions and partial differentiable with respect to x. We say that (Khastan et al. [49], Allahviranloo et al. [48], Mondal and Roy [53]):
are real valued functions and partial differentiable with respect to x. We say that (Khastan et al. [49], Allahviranloo et al. [48], Mondal and Roy [53]):
![]() is [(i)-p]-differentiable w.r.t. x at (x0, t0) if:
is [(i)-p]-differentiable w.r.t. x at (x0, t0) if:
![]()
![]() is [(ii)-p]-differentiable w.r.t. x at (x0, t0) if:
is [(ii)-p]-differentiable w.r.t. x at (x0, t0) if:
![]()
2.2.10. Definition 10
Let![]() , and
, and ![]() be [gH-p]-differentiable at
be [gH-p]-differentiable at ![]() with respect to x. We say that [48] [49]:
with respect to x. We say that [48] [49]:
![]() is [(i)-p]-differentiable w.r.t. x if:
is [(i)-p]-differentiable w.r.t. x if:
![]()
![]() is [(ii)-p]-differentiable w.r.t.x if:
is [(ii)-p]-differentiable w.r.t.x if:
![]()
3. Application of the Fuzzy Model to Vertical Infiltration
3.1. Formulation
We write Equation (14), in its fuzzy form as follows:
![]() (19)
(19)
with the new initial and boundary conditions:
![]()
where
![]() and
and![]() .(20)
.(20)
We can find solutions to the fuzzy problem (Equation (19)) and the initial and boundary conditions (Equation (20)), utilizing the theory developed in [46] [48] [54] [55], by translating the above fuzzy problem to a system of second order of crisp boundary value problems, hereafter called corresponding system of the fuzzy problem. Therefore, eight crisp BVPs systems are possible for the fuzzy problem {(1,1), (1,2), (1,3), (1,4), (2,1), (2,2), (2,3), (2,4)}.
(1,1) System (1,2) System
![]()
![]()
(1,3) System (1,4) System
![]()
![]()
(2,1) System (2,2) System
![]()
![]()
(2,3) System (2,4) System
![]()
![]()
We will hereby restrict ourselves to the solution of the (1,1) system, which is described in detail.
(1,1) system
![]() (21)
(21)
![]() (22)
(22)
In Figure 1 the membership function of ![]() is shown, in which
is shown, in which
the spread r is equal to 0.15.
3.1.1. Solution of the (1,1) System
1st case
![]() (23)
(23)
Boundary conditions
![]() (24)
(24)
Initial condition
![]() (25)
(25)
By setting ![]() in Equation (22), we take the following Laplace transformation:
in Equation (22), we take the following Laplace transformation:
![]() ,(26)
,(26)
with boundary conditions:
![]() (27)
(27)
The solution of Equation (26) becomes:
![]() (28)
(28)
The first derivative w.r.t. z is:
![]() (29)
(29)
The variable B(s) should be equal to 0, in order to satisfy the boundary condition (Equation (27)):
![]()
So, Equation (28) becomes:
![]() (30)
(30)
For the first condition for z = 0, we have:
![]() (31)
(31)
and Equation (30) becomes:
![]() (32)
(32)
Applying now the inverse Laplace transform [56] to Equation (32) we obtain the following equation:
![]() .(33)
.(33)
2nd case
![]() (34)
(34)
Boundary conditions
![]() (35)
(35)
Initial condition
![]()
In Equation (34) we set ![]() and we take the following Laplace transformation:
and we take the following Laplace transformation:
![]() ,(36)
,(36)
with boundary conditions:
![]() (37)
(37)
Applying the same process as in case 1, we have:
![]() (38)
(38)
Finally, the fuzzy solution is:
![]() (39)
(39)
In Equation (39) the fuzzy number ![]() is as follows:
is as follows:
![]() .(40)
.(40)
Existence statement of Equations ((21), (22))
Initial condition
Equation (39) satisfies the initial condition:
![]()
due to:
![]()
Boundary conditions
he first boundary condition is:
![]()
because it is:
![]()
The second boundary condition is:
![]()
We apply now the “L’Hospital Rule”
![]()
Thus, it is proven that the initial and boundary conditions of Equations ((23) and (34)) are satisfied.
Fuzzy derivatives
First Derivative of ![]() versus z:
versus z:
![]()
First Derivative of ![]() versus t:
versus t:
![]()
Second Derivative of C versus z:
![]()
We have now to prove:
![]() , or
, or![]() , or:
, or:
![]() (41)
(41)
where:
![]()
In the right part of Equation (41) we apply the theorem 1 of Bede and Gal [43]: For any ![]() with
with![]() , or
, or![]() , and any fuzzy number
, and any fuzzy number ![]() we have:
we have:![]() . Now the above equation becomes:
. Now the above equation becomes:
![]() (42)
(42)
By substituting in Equation (41) the above expressions of ![]() , we obtain:
, we obtain:
![]() e
e
As proven above, Equation (39) satisfies Equations ((23) and (34)), or their equivalent fuzzy Equation (19), provided that functions ![]() are both positive or both negative.
are both positive or both negative.
In order to investigate the positivity or negativity of the above functions, we set in ![]() and
and ![]() for simplicity,
for simplicity, ![]() and
and ![]() and we obtain:
and we obtain:
![]() (43)
(43)
where:
![]() ,(44)
,(44)
![]() (45)
(45)
Figure 2 and Figure 3 illustrate the dimensionless functions ![]() and
and ![]() versus ξ, for various values of η.
versus ξ, for various values of η.
As derived from Figure 3, ![]() is positive for every value of η, ξ and subsequently for all values of x and t. In order to examine the positivity of
is positive for every value of η, ξ and subsequently for all values of x and t. In order to examine the positivity of![]() , for a large spectrum of real soils, we examined 9 soils, whose properties are shown in Table 1. Soils 1 to 6 were taken from Nie et al. [57], while soils 7 to 9 were taken respectively from Evangelides [58], Sakellariou-Makrantonaki [59] and Sismanis [60]. The diffusion coefficients D were calculated from the Van Genuchten formula [56]:
, for a large spectrum of real soils, we examined 9 soils, whose properties are shown in Table 1. Soils 1 to 6 were taken from Nie et al. [57], while soils 7 to 9 were taken respectively from Evangelides [58], Sakellariou-Makrantonaki [59] and Sismanis [60]. The diffusion coefficients D were calculated from the Van Genuchten formula [56]:
![]() (46)
(46)
The Vadose zone thickness is considered approximately 15 m and the values
![]()
Figure 2. The function ![]() versus the dimensionless parameter ξ.
versus the dimensionless parameter ξ.
![]()
Figure 3. The function ![]() versus the dimensionless parameter ξ.
versus the dimensionless parameter ξ.
![]()
Table 1. The properties of the sample soils.
of η are derived from:![]() . In Figure 3, the function
. In Figure 3, the function ![]() is calculated for
is calculated for![]() . For this spectrum of values, the function is positive for values of ξ close to 1.
. For this spectrum of values, the function is positive for values of ξ close to 1.
It is derived as a conclusion that functions ![]() and (
and (![]() are both positive for all soils examined, thus the problem has a fuzzy solution.
are both positive for all soils examined, thus the problem has a fuzzy solution.
Fuzzy Infiltration rate and fuzzy cumulative Infiltration
The fuzzy infiltration rate is:
![]() ,(47)
,(47)
and the fuzzy cumulative infiltration is:
![]() (48)
(48)
4. Results and Discussion
The Fuzzy model was applied to 3 selected soils. These soils are shown in Table 1, as soil sample numbers 7 (Loamy sand, [58]), 8 (Sandy loam, [59]) and 9 (Sandy loam, [60]).
4.1. First Case, Sample Number 7, Loamy Sand
For the first case the following are valid:![]() ,
, ![]() ,
, ![]() ,
, ![]() and the solution is:
and the solution is:
![]() ,(49)
,(49)
where![]() .
.
In Figure 4, the soil water profiles![]() , in real times t = 5, 10, 30 and 60 min, approach
, in real times t = 5, 10, 30 and 60 min, approach ![]() at distances z = 450, 600, 1200, and 1800 cm respectively from the origin. In Figure 5 the membership function of the
at distances z = 450, 600, 1200, and 1800 cm respectively from the origin. In Figure 5 the membership function of the ![]() is illustrated in real times t = 5, 10, 30 and 60 min at z = 70 cm. In
is illustrated in real times t = 5, 10, 30 and 60 min at z = 70 cm. In
![]()
Figure 4. Moisture content profiles for t = 5, 10, 30, and 60 min for soil sample number 7.
![]()
Figure 5. Membership function of ![]() at z = 70 cm for soil sample number 7.
at z = 70 cm for soil sample number 7.
Figure 6, the fuzzy cumulative infiltration ![]() vs. t is illustrated, while in Figure 7, the fuzzy infiltration rate
vs. t is illustrated, while in Figure 7, the fuzzy infiltration rate ![]() versus time is shown for soil sample number 7.
versus time is shown for soil sample number 7.
4.2. Second Case, Sample Number 8, Sandy Loam
For the second case the following are valid:![]() ,
, ![]() ,
, ![]() ,
, ![]() and the solution is:
and the solution is:
![]() ,(50)
,(50)
where![]() .
.
In Figure 8, the soil water profiles![]() , in real times t = 5, 10, 30 and 60 min, approach
, in real times t = 5, 10, 30 and 60 min, approach ![]() at distances z = 300, 400, 700, and 1100 cm respectively from the origin. In Figure 9, the membership function of the
at distances z = 300, 400, 700, and 1100 cm respectively from the origin. In Figure 9, the membership function of the ![]() is
is
![]()
Figure 6. Fuzzy cumulative infiltration [𝐼] versus t for soil sample number 7.
![]()
Figure 7. Fuzzy infiltration rate [v0] versus t for soil sample number 7.
![]()
Figure 8. Moisture content profiles for t = 5, 10, 30, and 60 min for soil sample number 8.
![]()
Figure 9. Membership function of ![]() at z = 70 cm for soil sample number 8.
at z = 70 cm for soil sample number 8.
illustrated in real times t = 5, 10, 30 and 60 min at z = 70cm. In Figure 10, the fuzzy cumulative infiltration ![]() vs t is illustrated, while in Figure 11, the fuzzy infiltration rate
vs t is illustrated, while in Figure 11, the fuzzy infiltration rate ![]() versus time is shown for soil sample number 8.
versus time is shown for soil sample number 8.
4.3. Third Case, Sample Number 9, Sandy Loam
For the third case the following are valid:![]() ,
, ![]() ,
, ![]() ,
, ![]() and the solution is:
and the solution is:
![]() (51)
(51)
where![]() .
.
In Figure 12, the soil water profiles![]() , in real times t = 5, 10, 30 and 60 min, approach
, in real times t = 5, 10, 30 and 60 min, approach ![]() at distances z = 400, 500, 1000, and 1400 cm respectively from the origin. In Figure 13, the membership function of the
at distances z = 400, 500, 1000, and 1400 cm respectively from the origin. In Figure 13, the membership function of the
![]()
Figure 10. Fuzzy cumulative infiltration [𝐼] versus t for soil sample number 8.
![]()
Figure 11. Fuzzy infiltration rate [v0] versus t for soil sample number 8.
![]()
Figure 12. Moisture content profiles for t = 5, 10, 30, and 60 min for soil sample number 9.
![]()
Figure 13. Membership function of ![]() at z = 70 cm for soil sample number 9.
at z = 70 cm for soil sample number 9.
![]()
Figure 14. Fuzzy cumulative infiltration [𝐼] versus time t for soil sample number 9.
![]() is illustrated in real times t = 5, 10, 30 and 60 min at z = 70 cm. In Figure 14, the fuzzy cumulative infiltration
is illustrated in real times t = 5, 10, 30 and 60 min at z = 70 cm. In Figure 14, the fuzzy cumulative infiltration ![]() versus t is illustrated, while in Figure 15, the fuzzy infiltration rate
versus t is illustrated, while in Figure 15, the fuzzy infiltration rate ![]() versus time is shown for soil sample number 9.
versus time is shown for soil sample number 9.
Important Remark
As pointed out in introduction the linearized equation of Philip does not give accurate detailed description of flow profiles. However, this linear equation yields useful estimates of integral properties of cumulative infiltration I and of infiltration rate v0. In order to evaluate this property, we used the Valiantzas model [61], who has proposed a two-parameter vertical infiltration equation, located approximately at the middle of the domain of real soils. His model has compared with other nonlinear models providing accurate estimations of data:
![]() (52)
(52)
![]()
Figure 15. Fuzzy infiltration rate [v0] versus time t for soil sample number 9.
![]()
Figure 16. Comparison of the present crisp solution with the Valiantzas model.
Figure 16 illustrates a comparison of the present crisp solution (Second case, number 8) with the Valiantzas model. The two models have accurate approximation with a mean square error of 6.8 × 10−5.
5. Conclusions
The Bede and Stefanini [46] theory with the generalized Hukuhara (g-H) derivative, as well as its extension on differential equations [48], allows researchers to solve practical problems, useful in engineering. It is now possible for engineers to take the fuzziness of various parameters involved into consideration, when calculating and deciding on their work.
Vertical infiltration linear equation regarding the water movement in vadose zone has a fuzzy solution with a function ![]() being [gH – p] differentiable.
being [gH – p] differentiable.
The fuzziness of soil water movement diminishes as flow moves up in vertical direction. The fuzziness of cumulative infiltration rises vs time and the fuzziness of infiltration rate diminishes vs time.
Since there exist no previous treatments of the problem of vertical infiltration with Fuzzy Logic, comparison of the results of the present work is only possible between crisp solutions and the fuzzy solution. The difference between crisp solution (CS) and fuzzy solution (FS) appearing in Figures 4-15, remains constant
![]() for every value of α-cut. So, there is a serious problem for
for every value of α-cut. So, there is a serious problem for
irrigation systems to be calculated with crisp solution, without considering the fuzziness of the problem. It is important for engineers and researchers to take into account uncertainties of such magnitude in order to proceed to decision making. More specifically, in problems of Irrigation and Drainage Engineering, the related design of irrigation and drainage networks can be more accurate if the possible lower and higher limits of the water-front are known beforehand.
As is pointed in the remark, the linearized solution estimates well the phenomena of cumulative Infiltration and Infiltration rate for real soils.
Author Contributions
Conceptualization, C.T.; methodology, C.T. and G.P.; validation C.T. and K.P.; writing, C.T., G.P. and K.P.; review and editing, G.A. and C.E.; supervision, C.T. and C.E.