Empirical Likelihood Inference for Generalized Partially Linear Models with Longitudinal Data

Jinghua Zhang^1,2, Liugen Xue¹

¹College of Applied Sciences, Beijing University of Technology, Beijing, China.
²Department of Information Engineering, Jingdezhen Ceramic Institute, Jiangxi, China.

DOI: 10.4236/ojs.2020.102014                

Abstract

In this article, we propose a generalized empirical likelihood inference for the parametric component in semiparametric generalized partially linear models with longitudinal data. Based on the extended score vector, a generalized empirical likelihood ratios function is defined, which integrates the within-cluster correlation meanwhile avoids direct estimating the nuisance parameters in the correlation matrix. We show that the proposed statistics are asymptotically Chi-squared under some suitable conditions, and hence it can be used to construct the confidence region of parameters. In addition, the maximum empirical likelihood estimates of parameters and the corresponding asymptotic normality are obtained. Simulation studies demonstrate the performance of the proposed method.

Keywords

Longitudinal Data, Generalized Partially Linear Models, Empirical Likelihood, Quadratic Inference Function

1. Introduction

An important issue in statistical inference is to construct the confidence region for parameters of interest. The convention method is the normal approximation method which based on the asymptotic normal distribution of parameter estimators. The normal approximation (NA) method requires estimating the limiting variance of regression parameter, which is very complicated in some situation. Besides, the confidence region derived from the NA method is predetermined to be symmetric.

As a nonparametric data-driven technique, the empirical likelihood (EL) approach employs empirical likelihood function without specifically assuming a distribution for the data, while it can incorporate the side information through constraints, which maximizes the efficiency of the method. Compare with the NA method, EL approach does not involve a plug-in estimation for the limiting variance, and the shapes and the orientation of the confidence region obtained are automatically determined by the data. There has been a lot of literature in empirical likelihood, e.g., [1] - [12].

Longitudinal data often occurs in biomedical research where the repeated measurements form subjects are collected over times, and therefore the responses from same subjects are very likely to be correlated with an unknown structure. The challenge for longitudinal data lies in how to effectively utilize the within-cluster information. The early works in EL for longitudinal data ignored the correlations within subjects, e.g. [7] [8]. Some recent studies incorporate the correlation information by constructing the auxiliary random vector through the generalized estimating equations (GEEs) [9] [10]. The GEEs use a working correlated matrix to carry the correlation information. The working correlated matrix is decided by a small set of nuisance parameters $\alpha$ to avoid the specification of the whole correlation matrix [13]. The advantage of the GEEs is that the estimators of the regression parameter $\beta$ are always consistent. However, GEEs estimator suffers a great loss in efficiency when the correlation structure is misspecified. The quadratic inference functions (QIFs) approach avoids estimating the nuisance correlation parameters $\alpha$ by assuming that the inverse of the working correlation matrix can be approximated by a linear combination of several known basis matrices, and solve the combined estimation functions by using the principle of the generalized method of moments [14] [15]. The QIFs can also take the within-cluster correlation into account and is more efficient than GEEs when the working correlation is misspecified. The QIFs approach has been applied to many models, including varying coefficient models, partially linear models, single-index models and generalized linear models. The recent related works include [16] - [21]. More recently, [11] [12] proposed generalized empirical likelihood method (GEL), which using a QIFs-based generalized log-empirical likelihood ratio statistics to construct the confidence region for the parameters in generalized linear models (GLMs) with longitudinal data and partially linear models with Longitudinal data.

Generalized partially linear models (GPLMs) can be regarded as a comprise between the GLMs and fully nonparametric models. The choice of a partial linear model is sometimes made to avoid nonparametric specification of high-dimensional covariates, and at other times the model arises naturally due to categorical covariates. In this article, we extend the GEL method to GPLMs with longitudinal data and the B-spline method is adopted to approximate the nonparametric component in the model. Our method incorporates the within-cluster correlation information into the auxiliary random vector. Our proposed method does not require the estimation of the variance of the proposed estimator and is not sensitive to the misspecification of the working correlation structure.

The rest of this article is organized as follows. We propose the QIF-based EL method for GPLMs in Section 2 and present the corresponding asymptotic results in Section 3. Simulation studies are provided in Section 4 and a real data is analysed in Section 5. The details of the proofs are provided in the Appendix.

2. Model and Generalized Empirical Likelihood

2.1. GPLMs with Longitudinal Data

In this article, we consider a longitudinal study with n subjects and $m_i$ observations over time for the ith subject ( $i=1,\cdots ,n$ ), for a total of $N={\displaystyle {\sum }_{i=1}^n}{m}_i$ observations. Each observation consists of a response variable $Y_{ij}$ and the covariate vectors $\left(X_{ij}\mathrm{,}{U}_{ij}\right)$ , where $X_{ij}\in R^p$ and $U_{ij}$ is a scalar. We assume that the observations from different subjects are independent, but those from the same subject are dependent. The generalized partially linear model (GPLMs) with longitudinal data take the form

${\mu }_{ij}=E\left(Y_{ij}|X_{ij},U_{ij}\right)=h\left(X_{ij}^{\text{T}}\beta +\alpha \left(U_{ij}\right)\right),\mathrm{var}\left(Y_{ij}|X_{ij},U_{ij}\right)=v\left({\mu }_{ij}\right).$ (1)

where $\beta =\left({\beta }_1\mathrm{,}\cdots \mathrm{,}{\beta }_p\right)$ is a $p\times 1$ vector of unknown regression coefficients, $h(\cdot )$ is a known monotonic smooth link function, $\alpha (\cdot )$ is a unknown smooth function and $v(\cdot )$ is a known function with $v(\cdot )>0$ . Without loss of generality, we assume $U~U\left(\mathrm{0,1}\right)$ .

Following [22], we replace $\alpha (\cdot )$ by its basis function approximations. More specifically, let $B\left(u\right)={\left(B_1\left(u\right),\cdots ,B_L\left(u\right)\right)}^{\text{T}}$ be the B-spline basis functions with the order of M, where $L=K+M+1$ , and K is the number of interior knots. We use the B-spline basis functions because they often provide good approximations with a small number of knots. Besides, the B-spline basis functions have bounded support and are numerically stable. The spline approach also treats a non-parametric function as a linear function with the basis functions being the pseudo-design variables, thus any computational algorithm developed for the generalized linear models can be used for the generalized partially linear models.

Suppose $\alpha \left(u\right)$ can be approximated by $\alpha \left(u\right)\approx B{\left(u\right)}^{\text{T}}\gamma$ , where $\gamma ={\left({\gamma }_1\mathrm{,}\cdots \mathrm{,}{\gamma }_L\right)}^{\text{T}}$ is a $L\times 1$ vector of unknown regression coefficients. Then our regression model (1) becomes

${\mu }_{ij}\left(\beta \mathrm{,}\gamma \right)=h\left(X_{ij}^{\text{T}}\beta +B{\left(U_{ij}\right)}^{\text{T}}\gamma \right)\mathrm{,}$ (2)

Denote $\theta ={\left({\theta }_1,\cdots ,{\theta }_p,{\theta }_{p+1},\cdots ,{\theta }_{p+L}\right)}^{\text{T}}={\left({\beta }^{\text{T}},{\gamma }^{\text{T}}\right)}^{\text{T}},Y_i={\left(Y_{i1},\cdots ,Y_{i{m}_i}\right)}^{\text{T}}$ , and write $X_i\mathrm{,}{U}_i\mathrm{,}B\left(U_i\right)\mathrm{,}{\mu }_i$ in a similar fashion. Following the QIFs approach, the extend score $g_N\left(\theta \right)$ is defined to be

$g_N\left(\theta \right)=\frac{1}{n}{\displaystyle \underset{i=1}{\overset{n}{\sum }}}{g}_i\left(\theta \right)=\frac{1}{n}{\displaystyle \underset{i=1}{\overset{n}{\sum }}}\left(\begin{array}{c}{\stackrel{\dot{}}{\mu }}_i^{\text{T}}{A}_i^{-1/2}{M}_1{A}_i^{-1/2}\left(Y_i-{\mu }_i\right)\\ ⋮\\ {\stackrel{\dot{}}{\mu }}_i^{\text{T}}{A}_i^{-1/2}{M}_s{A}_i^{-1/2}\left(Y_i-{\mu }_i\right)\end{array}\right),$ (3)

where ${\stackrel{\dot{}}{\mu }}_i^{}=\frac{\partial {\mu }_i}{\partial \theta },$ $A_i^{}=\text{diag}\left(v\left({\mu }_{i1}\right),\cdots ,v\left({\mu }_{im}\right)\right)$ is the marginal covariance matrix of the ith subject and $M_1\mathrm{,}\cdots \mathrm{,}{M}_s$ are known matrices for approximating the inverse of the working correlation matrix $R\left(\rho \right)$ in GEEs. Then $\hat{\theta }$ is obtained by minimizing the following quadratic inference function

${\mathcal{Q}}_n\left(\theta \right)=n{g}_N^{\text{T}}\left(\theta \right){\Omega }_N{\left(\theta \right)}^{-1}{g}_N\left(\theta \right)\mathrm{,}$ (4)

where ${\Omega }_N\left(\theta \right)=\frac{1}{n}{\displaystyle {\sum }_{i=1}^n}{g}_i\left(\theta \right)g_i{\left(\theta \right)}^{\text{T}}$ .

Hence, $\hat{\beta }={\left({\hat{\theta }}_1\mathrm{,}\cdots \mathrm{,}{\hat{\theta }}_p\right)}^{\text{T}}$ is the QIF estimator of $\beta$ , and the estimator of $\alpha \left(u\right)$ can be obtained by $\hat{\alpha }\left(u\right)=B{\left(u\right)}^{\text{T}}\hat{\gamma }$ , where $\hat{\gamma }={\left({\hat{\theta }}_{p+1}\mathrm{,}\cdots \mathrm{,}{\hat{\theta }}_{p+L}\right)}^{\text{T}}$ is the QIF estimator of $\gamma$ . Details of the QIFs estimator for GPLMs with longitudinal data refers to [21].

2.2. GEL for GPLMs with Longitudinal Data

In most applications of GPLMs, the main interest is the statistical inference on the regression coefficient ${\beta }_0$ . Similar with [5], we regard the nonparametric function $\alpha (\cdot )$ , i.e. the spline coefficient $\gamma$ as nuisance, and conduct a suitable estimator of it to make sure the efficient statistical inference for $\beta$ . In this article, we take the QIF estimate $\hat{\gamma }$ as the estimator of $\gamma$ .

Noticing $g_i\left(\theta \right)$ in (3) carries the within-cluster correlation information, in order to construct the empirical likelihood ratio function for, we introduce the auxiliary random vector

(5)

Note that 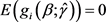when, we define the generalized empirical log-likelihood ratio function as follows,

(6)

By the Lagrange multiplier method, we obtain that 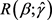is maximized at

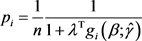(7)

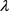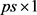where is a vector satisfies

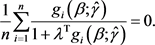(8)

Then can be represented as

(9)

By minimizing under the Equation constraints (8), we can obtain the maximum empirical likelihood estimator (MELE) of the parameter.

3. Asymptotic Properties

For convenience and simplicity, let C denote a positive constant that may have different values at each appearance throughout this paper and 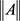denote the modulus of the largest singular value of matrix or vector A. Before the proof of our main theorems, we list some regularity conditions that used in this paper.

Assumption (A1): The spline regression parameter is identifiable, that is, is the spline coefficient vector from the spline approximation to. In addition, there is a unique satisfying, where S is the parameter space.

Assumption (A2): The weight matrix converges almost surely to a constant matrix, where is invertible.

Assumption (A3): The covariate matrices satisfy that .

Assumption (A4): The error satisfies that , and there exists a postive constant such that .

Assumption (A5): All marginal variances and.

Assumption (A6): is a bounded sequence of positive integers.

Assumption (A7): is rth continuous differentiable on (0, 1), where.

Assumption (A8): The inner knots satisfy

where

Assumption (A9): The link function is 2nd continuous differentiable and for some.

[Remark] (A1) is for the identification. (A2) holds when based on the weak law of large numbers when n goes to infinity and the maximum cluster size is fixed, i.e., when (A6) holds. (A3)-(A6) are the common regularity conditions in the longitudinal data analysis. (A7) is the usual assumption in spline approximation, it determines the convergence rate of spline estimate. (A8) is the general condition for the knots in B-spline approximation. (A9) is the common condition in the study of GLMs.

We next study the asymptotic properties of the resulting GEL estimators. We first introduce some notations. Let denote the true values of and be the MELE of. The following Theorem 1 shows that the is asymptotically distributed as a Chi-square with ps degrees of freedom.

Lemma 1. Suppose that the regularity conditions of (A1)-(A9) hold and the numbers of knots, then

This is a direct result from Theorem 1 of [21].

Lemma 2. Suppose that the regularity conditions of (A1)-(A9) hold and the numbers of knots, then

(10)

(11)

The proof can be found in the Appendix.

Theorem 1. Assume that the conditions (A1)-(A9) hold and the numbers of knots, then

where represents the convergence in distribution.

The proof can be found in the Appendix.

Let be the quantile of for any. From Theorem 1, an approximate confidence region can be established by

Denote

If the matrices and are invertible, we obtain the asymptotic normality of.

Theorem 2. Suppose that the conditions (A1)-(A9) hold and the numbers of knots, then

where.

The proof can be found in the Appendix.

The confidence region interval of each component of is also worth concerning. Let denote the unit vector with 1 at the rth entry, for. The estimate of the rth component of is, for. Let

where is the identity matrix, is the Kronecker product, and is defined in (5). Then, the partial generalized empirical log-likelihood ratio for is defined as

Theorem 3. Assume that the conditions (A1)-(A9) and the numbers of knots, if is the true parameter, then

The proof of Theorem 3 is similar to that of Theorem 1, we hence omit here.

Applying Theorem 3, the approaximate confidence interval for can be constructed by

4. Simulation Studies

In this section, we conduct simulation studies to evaluate the finite sample performance of the proposed methods. We compare the GEL with the NA-based method in terms of the coverage probability and the lengths of the obtained confidence region.

In our non-parametric estimation implementation, we use the sample quantiles of as knots. Moreover, we use cubic splines and take the number of internal knots to be the integer around. This particular choice is consistent with the asymptotic theory in Section 3 and performs well in the simulations.

4.1. Study 1

Consider a binomial response:

where and 150,. The clustered binary responses are generated as [23]. The correlation parameter are taken to be 0.25, 0.5 and 0.75 which represent weak, medium and strong correlation respectively. We generated 500 data sets for each pair of ().

Table 1 list the EL-based and NA-based confidence intervals of under CS structure. It shows that the GEL approach gives a slightly shorter confidence intervals than the NA method, while the former has a coverage probability more

Table 1. The average length and the corresponding coverage probabilities of the 95% confidence region of for GEL and NA when the correlation structure is CS.

closer to the nominal level. In addition, the coverage probability obtained by GEL approach tend to the nominal level and the average length decrease as n increases.

To study the influence of mis-specification to GEL approach, we derive the GEL confidence interval when the working correlation structure is specified to be CS and AR-1 respectively. Table 2 list the results when the true structure is CS. Table 3 list the results when the true structure is AR-1. It is known that the QIFs estimator is insensitive to mis-specification in correlation structure. Table 2 and Table 3 show that the QIFs-based GEL approach gives similar 95% confidence interval and coverage probability even the correlation structure is misspecified, which means the proposed GEL approach is robust.

Table 2. The average length and the corresponding coverage probabilities of the 95% confidence region of for GEL when the true correlation structure is CS.

Table 3. The average length and the corresponding coverage probabilities of the 95% confidence region of for GEL when the true correlation structure is AR-1.

4.2. Study 2

We consider a two-demensional logistic model with, and

where and are drawn independently from a uniform distribution on. The clustered binary responses with exchangeable correlation structure are also generated as [23]. The correlation parameter are taken to be 0.3 and 0.8.

Carried out 200 simulation runs, the EL-based and NA-based 95% confidence intervals for when are reported in Figure 1. It shows that GEL approach gives a smaller confidence region than the NA method. As to the coverage probability, the GEL approach is more closer to the nominal level than NA (0.925 vs 0.90). The result of is similar, we omit here.

5. Example: Infectious Disease Data

To investigate the performance of the proposed method, we analysis an infectious disease data. In this study, a total of 275 preschool children were examined every three months for 18 months. The outcome is the presence of respiratory infection (1 = yes, 0 = no). The primary interest is in studying the relationship of the risk of respiratory infection to Vitamin A deficiency, which is indicated by xerophthalmia variable (1 = yes, 0 = no). The other covariates included: age,

Figure 1. The 95% confidence region of based on GEL and NA approach when for Study 2.

Figure 2. The 95% confidence region of based on GEL and NA approach under exchangeable correlation structure for infectious disease data.

gender (1 = female, 0 = male), height, stunting status (1 = yes, 0 = no), and the seasonal Cosine and seasonal sine variables which indicate the season when those examinations took.

This data set has been well analyzed by many authors, such as [24] [25] [26] [27] [28]. We here consider a simple logistic model:

where is the mean of the risk of respiratory infection, and describe the effects of Vitamin A deficiency and the sex aspect. We use two methods: the NA method and QIFs-based GEL under the CS correlation. The confidence regions are reported in Figure 2. It shows that GEL gives smaller confidence regions than NA does.

Acknowledgements

We thank the Editor and the referees for their comments. The research is funded by the National Natural Science Foundation of China (11571025) and the Beijing Natural Science Foundation (1182008). This support is greatly appreciated.

Appendix

Proof of Lemma 2

Proof. Consider the kth component of:

(12)

Note that

(13)

Apply Taylor expansion to the first two terms in (13) at, we obtain

(14)

where is between and, is between and , and

Substitute (14) into (12), we obtian

From conditions (A7), (A8) and theorem 12.7 in [29], we have and. Then, invoking conditions (A3)-(A5), by a simple calculation, we have and .

Invoking conditions (A4)-(A9), by lemma 1 , we have and.

Denote

we have

Follow [11], we obtain

i.e.

Similarly, (11) can be proved. Thus we complete the proof of the Lemma 2.

Follow the argument of [4], we can prove

(15)

Proof of Theorem 1

Proof. Applying Taylor expansion to, we obtain

Recall (8), it follows that

This together with Lemma 1 and (15) proves that

and

Therefore, we have

Together with Lemma 2, we complete the proof of Theorem 1.

Proof of Theorem 2

Proof. We first define bivariate functions and respectively as

Under the condition (A1), if is the MELE of and is the root of (8), following Lemma 1 of [3], we have

Expanding and at, together with conditions (A6)-(A9) and Lemma 2, we have

Conflicts of Interest

The authors declare no conflicts of interest.

References

[1]	Owen, A. (1988) Empirical Likelihood Ratio Confidence Intervals for a Single Function. Biometrika, 75, 237-249. https://doi.org/10.1093/biomet/75.2.237
[2]	Owen, A. (1990) Empirical Likelihood and Confidence Regions. Annals of Statistics, 18, 90-120. https://doi.org/10.1214/aos/1176347494
[3]	Qin, J. and Lawless, J.F. (1994) Empirical Likelihood and General Estimating Equations. Annals of Statistics, 22, 300-325. https://doi.org/10.1214/aos/1176325370
[4]	Owen, A. (2001) Empirical Likelihood. Chapman & Hall, London. https://doi.org/10.1201/9781420036152
[5]	Shi, J. and Lau, T.S. (2000) Empirical Likelihood for Partially Linear Models. Journal of Multivariate Analysis, 72, 132-148. https://doi.org/10.1006/jmva.1999.1866
[6]	Wang, Q.H. and Jing, B. (2003) Empirical Likelihood for Partially Linear Models. Annals of the Institute of Statistical Mathematics, 55, 585-595. https://doi.org/10.1007/BF02517809
[7]	Xue, L.G. and Zhu, L.X. (2007) Empirical Likelihood Semiparametric Regression Analysis for Longitudinal. Biometrika, 94, 921-937. https://doi.org/10.1093/biomet/asm066
[8]	Xue, L.G. and Zhu, L.X. (2008) Empirical Likelihood-Based Inference in a Partially Linear Model for Longitudinal Data. Science in China, Ser A, 51, 115-130. https://doi.org/10.1007/s11425-008-0020-4
[9]	Bai, Y., Fung, W.K. and Zhu, Z.Y. (2010) Weighted Empirical Likelihood for Generalized Linear Models with Longitudinal Data. Journal of Statistical Planning and Inference, 140, 3446-3456. https://doi.org/10.1016/j.jspi.2010.05.007
[10]	Qu, G.Y., Bai, Y. and Zhu, Z.Y. (2012) Robust Empirical Likelihood Inference for Generalized Partial Linear Models with Longitudinal Data. Journal of Multivariate Analysis, 105, 21-44. https://doi.org/10.1016/j.jmva.2011.08.003
[11]	Tian, R.Q., Xue, L.G. and Liu, C.L. (2014) Generalized Empirical Likelihood Inference in Generalized Linear Models for Longitudinal Data. Communications in Statistics—Theory and Methods, 43, 3893-3904. https://doi.org/10.1080/03610926.2012.719987
[12]	Tian, R.Q. and Xue, L.G. (2017) Generalized Empirical Likelihood Inference in Partial Linear Models for Longitudinal Data. Statistics, 51, 988-1005. https://doi.org/10.1080/02331888.2017.1355370
[13]	Liang, K.L. and Zeger, S.L. (1986) Longitudinal Data Analysis Using Generalized Estimating Equations. Biometrika, 73, 13-22. https://doi.org/10.1093/biomet/73.1.13
[14]	Qu, A., Lindsay, B.G. and Li, B. (2000) Improving Generalized Estimating Equations Using Quadratic Inference Functions. Biometrika, 87, 823-836. https://doi.org/10.1093/biomet/87.4.823
[15]	Hansen, L.P. (1982) Large Sample Properties of Generalized Method of Moments Estimators. Econometrica, 50, 1029-1054. https://doi.org/10.2307/1912775
[16]	Qu, A. and Song, X.K. (2004) Assessing Robustness of Generalized Estimating Equations and Quadratic Inference Functions. Biometrika, 91, 447-459. https://doi.org/10.1093/biomet/91.2.447
[17]	Qu, A. and Li, R. (2006) Quadratic Inference Functions for Varying Coefficient Models with Longitudinal Data. Biometrics, 62, 379-391. https://doi.org/10.1111/j.1541-0420.2005.00490.x
[18]	Zhou, J.L. and Qu, A. (2012) Informative Selection for Correlation Structure for Longitudinal Data. Journal of the American Statistical Association, 107, 701-710. https://doi.org/10.1080/01621459.2012.682534
[19]	Wang, L., Xue, L., Qu, A. and Liang, H. (2014) Estimation and Model Selection in Generalized Additive Partial Linear Models for Correlated Data with Diverging Number of Covariates. Annals of Statistics, 42, 592-694. https://doi.org/10.1214/13-AOS1194
[20]	Tian, R.Q., Xue, L.G. and Liu, C.L. (2014) Penalized Quadratic Functions for Semiparametric Varying Coefficient Partially Linear Models with Longitudinal Data. Journal of Multivariate Analysis, 132, 94-110. https://doi.org/10.1016/j.jmva.2014.07.015
[21]	Zhang, J.H. and Xue, L.G. (2017) Quadratic Inference Functions for Generalized Partially Linear Models with Longitudinal Data. Chinese Journal of Applied Probability and Statistics, 33, 409-416. http://aps.ecnu.edu.cn/EN/10.3969/j.issn.1001-4268.2017.04.007
[22]	He, X., Zhu, Z.Y. and Fung, W.K. (2002) Estimation in a Semiparametric Model for Longitudinal Data with Unspecified Dependence Structure. Biometrika, 89, 579-590. https://doi.org/10.1093/biomet/89.3.579
[23]	Oman, S.D. (2009) Easily Simulated Multivariate Binary Distributions with Given Positive and Negative Correlations. Computational Statistics & Data Analysis, 53, 999-1005. https://doi.org/10.1016/j.csda.2008.11.017
[24]	Lin, X.H. and Carroll, R.J. (2001) Semiparametric Regression for Clustered Data. Biometrika, 88, 1179-1185. https://doi.org/10.1093/biomet/88.4.1179
[25]	Lin, X.H. and Carroll, R.J. (2001) Semiparametric Regression for Clustered Data Using Generalized Estimating Equations. Journal of the American Statistical Association, 96, 1045-1056. https://doi.org/10.1198/016214501753208708
[26]	He, X.M., Fung, W.K. and Zhu, Z.Y. (2005) Robust Estimation in a Generalized Partially Linear Model for Cluster Data. Journal of the American Statistical Association, 100, 1176-1184. http://doi.org/10.1198/016214505000000277
[27]	Zeger, S.L. and Karim, M.R. (1991) Generalized Linear Models with Random Effects: A Gibbs Sampling Approach. Journal of the American Statistical Association, 86, 79-86. https://doi.org/10.1080/01621459.1991.10475006
[28]	Diggel, P.J., Liang, K.Y. and Zeger, S.L. (1994) Analysis of Longitudinal Data. Oxford University Press, Oxford.
[29]	Schumaker, G. (1981) Spline Function. Wiley, New York.