Variable Selection via Biased Estimators in the Linear Regression Model ()
1. Introduction
Due to the simplicity and interpretability, linear regression models play a significant role in modern statistical methods. The linear regression model aspires to find the linear relationship between the dependent variable and the non-stochastic explanatory variables for the prediction purpose.
Let us consider the linear regression model
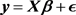(1)
where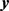 
is the 
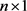vector of observations on the dependent variable, 
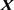is the 
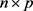matrix of observations on the non-stochastic predictor variables, 
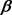is a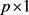 
vectors of unknown coefficients, and 
is the 
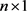vector of random error terms, which is independent and identically normally distributed with mean zero and common variance
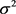, that is 
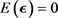and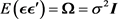
.
It is well known that the Ordinary Least Square Estimator (OLSE) is the Best Linear Unbiased Estimator (BLUE) for finding the unknown parameter vector in model (1), which can be obtained by minimizing Error Sum of Squares (ESS),
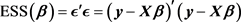(2)
with respect to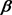
, and defined as
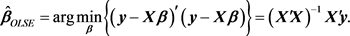(3)
However, the OLSE is unstable and produces parameter estimates with high variance when multicollinearity exists on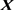
. As a curative action to the multicollinearity problem, the biased estimators have been used by many researchers. The following biased estimators are popular in statistical literature:
• Principal Component Regression Estimator (PCRE) [1]
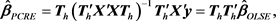(4)
where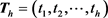 
is the first h columns of the standardized eigenvectors of![]()
.
• Ridge Estimator (RE) [2]
![]()
(5)
where ![]()
is the regularization parameter, and ![]()
is the ![]()
identity matrix.
• r-k class estimator [3]
![]()
(6)
Note that r-k class estimator is a combination of PCRE and RE.
• Almost Unbiased Ridge Estimator (AURE) [4]
![]()
(7)
• Liu Estimator (LE) [5]
![]()
(8)
where ![]()
is the regularization parameter.
• Almost Unbiased Liu Estimator (AULE) [6]
![]()
(9)
• r-d class estimator [7]
![]()
(10)
Note that r-d class estimator is a combination of PCRE and LE.
According to Kayanan and Wijekoon [8], the generalized form to represent the estimators RE, AURE, LE, AULE, PCR, r-k class estimator and r-d class estimator is given by
![]()
(11)
where
![]()
In recent studies, Kayanan and Wijekoon [8] have shown that r-k class estimator and r-d class estimator outperformed other estimators for the selected range of regularization parameter values when multicollinearity exists among the predictor variables. However, biased estimators introduce heavy bias when the number of predictor variables is high, and the final model may contain some irrelevant predictor variables as well. To handle this issue, Tibshirani [9] proposed the Least Absolute Shrinkage and Selection Operator (LASSO) as
![]()
(12)
where ![]()
is a turning parameter. Note that we cannot find an analytic solution for LASSO since ![]()
is a non-differentiable function. Tibshirani [9] and Fu [10] have used the standard quadratic programming technique and shooting algorithm, respectively, to find solutions for LASSO. Apart from these two methods, the Least Angle Regression (LARS) algorithm proposed by Efron et al. [11] is a popular one in the recent literature to find LASSO solutions. The LASSO wields both the multicollinearity problem and variable selection simultaneously in the linear regression model. However, LASSO failed to outperform RE if high multicollinearity exists among predictors, and it is unsteady when the number of predictors is higher than the number of observations [12]. To overcome this problem, Zou and Hastie [12] proposed Elastic net (ENet) estimator by combining LASSO and RE as
![]()
(13)
The LARS-EN algorithm, which is a modified version of the LARS algorithm, has been used to obtain solutions for ENet.
In this work, we propose generalized version of LARS algorithm that can be combined LASSO with other biased estimators such as AURE, LE, AULE, PCRE, r-k class and r-d class estimators. Further, we compared the prediction performance of proposed algorithm with existing algorithms of LASSO and Enet using a Monte-Carlo simulation study and real-world examples. The structure of the rest of the article is as follows: Section 2 contains proposed algorithms, Section 3 shows the comparison of proposed algorithm, Section 4 concludes the article, and references are provided at the end of the paper.
2. Generalized Least Angle Regression (GLARS) Algorithm
Based on Efron et al. [11] and Hettigoda [13], now we propose GLARS algorithm as follows:
Step 1: Standardize the predictor variables ![]()
to have a mean of zero and a standard deviation of one, and response variable ![]()
to have a mean zero.
Step 2: Start with the initial estimated value of ![]()
as![]()
, and the residual![]()
.
Step 3: Find the predictor ![]()
most correlated with ![]()
as follows
![]()
(14)
Then increase the estimate of ![]()
from 0 until any other predictor ![]()
has a high correlation with the current residual as ![]()
does. At this point, GLARS proceeds in the equiangular direction between the two predictors ![]()
and ![]()
instead of continuing in the direction based on![]()
.
In a similar way, the ith variable ![]()
eventually earns its way into the active set, and then GLARS proceeds in the equiangular direction between![]()
. Continue adding variables to the active set in this way moving in the direction defined by the least angle direction. In the intermediate steps, the coefficient estimates are updating using the following formula:
![]()
(15)
where ![]()
is a value between [0,1] which represents how far the estimate moves in the direction before another variable enters the model and the direction changes again, and ![]()
is the equiangular vector.
The direction ![]()
is calculated using the following formula:
![]()
(16)
where ![]()
is the matrix with column![]()
, ![]()
be the jth standard unit vector in ![]()
which has the index of variables selected in each subsequent steps, and ![]()
is a generalized variable which can be substituted by respective expressions for any of estimators of our interest as listed in Table 1. Then, ![]()
is calculated as follows:
![]()
(17)
where
![]()
(18)
for any j such that![]()
, and
![]()
(19)
for any j such that![]()
.
Step 4: If![]()
, then ![]()
is the matrix formed by removing the column ![]()
from![]()
. Then the residual ![]()
related to the current step is calculated as
![]()
(20)
and then move to the next step where ![]()
is the value of j such that ![]()
or ![]()
or![]()
.
Step 5: Proceed Step 3 until![]()
.
In Table 1, ![]()
is the ![]()
identity matrix, ![]()
is the number of selected variables in each subsequent step, and ![]()
is the first ![]()
columns of the standardized eigenvectors of![]()
.
2.1. Properties of GLARS
GLARS algorithm sequentially updates the combined estimates of LASSO and other estimators. It requires ![]()
operations, where m is the number of steps. The prediction performance of the GLARS is evaluated using the Root
![]()
Table 1. ![]()
of the estimators for GLARS.
Mean Square Error (RMSE) criterion, which is described in Section 3. We can use GLARS to combine LASSO and any of estimators as listed in Table 1.
Note that GLARS provides LASSO and ENet solutions when ![]()
equals to the corresponding expressions of OLSE and RE, respectively. For simplicity, we refer GLARS as LARS-LASSO, LARS-EN, LARS-AURE, LARS-LE, LARS-AULE, LARS-PCRE, LARS-rk and LARS-rd when ![]()
equals to the corresponding expressions of OLSE, RE, AURE, LE, AULE, PCRE, r-k class and r-d class estimators, respectively.
2.2. Selection of Regularization Parameter Values
According to Efron et al. [11] and Zou and Hastie [12], the conventional tuning parameter of LARS-LASSO is![]()
, and LARS-LASSO automatically controls it. The regularization parameter k of LARS-EN is selected using 10-fold cross-validation for each t. Similarly, we choose the regularization parameter k or d of proposed algorithms using 10-fold cross-validation for each t.
3. Comparison of Proposed Algorithms
Proposed algorithms are compared with the LARS-LASSO and LARS-EN algorithms using the RMSE criterion, which is the expected prediction error of the algorithms, and is defined as
![]()
(21)
where ![]()
denotes the new data which are not used to obtain the parameter estimates, and ![]()
is the estimated value of ![]()
using the respective algorithm. A Monte Carlo simulation study and the real-world examples are used for the comparison.
3.1. Simulation Study
According to McDonald and Galarneau [14], first we generate the predictor variables by using the following formula:
![]()
(22)
where ![]()
is an independent standard normal pseudo random number, and ![]()
is the theoretical correlation between any two explanatory variables.
In this study, we have used a linear regression model of 100 observations and 20 predictors. A dependent variable is generated by using the following equation
![]()
(23)
where ![]()
is a normal pseudo random number with mean zero and common variance![]()
.
We choose ![]()
as the normalized eigenvector corresponding to the largest eigenvalue of ![]()
for which![]()
. To investigate the effects of different degrees of multicollinearity on the estimators, we choose ![]()
, which represents weak, moderated and high multicollinearity. For the analysis, we have simulated 50 data sets consisting of 50 observations to fit the model and 50 observations to calculate the RMSE. The Cross-validated RMSE of the algorithms are displayed in Figures 1-3, and the median cross-validated RMSE of the algorithms are displayed in Table 2-4.
From Figures 1-3 and Tables 2-4, we can observe that LARS-PCRE, LARS-rk and LARS-rd algorithms show better performance compared to other algorithms in weak, moderated and high multicollinearity, respectively.
![]()
Figure 1. Cross-validated RMSE values of the algorithms when![]()
.
![]()
Figure 2. Cross-validated RMSE values of the algorithms when![]()
.
![]()
Figure 3. Cross-validated RMSE values of the algorithms when![]()
.
![]()
Table 2. Median cross-validated RMSE values when![]()
.
![]()
Table 3. Median cross-validated RMSE values when![]()
.
![]()
Table 4. Median Cross-validated RMSE values when![]()
.
3.2. Real-World Examples
Two real-world examples, namely the Prostate Cancer Data [15], and the UScrime dataset [16], are considered to compare the performance of the proposed algorithms.
Prostate Cancer Data: In the Prostate Cancer Data, the predictors are eight clinical measures: log cancer volume (lcavol), log prostate weight (lweight), age, log of the amount of benign prostatic hyperplasia (lbph), seminal vesicle invasion (svi), log capsular penetration (lcp), Gleason score (gleason) and percentage Gleason score 4 or 5 (pgg45). The response is the log of prostate specific antigen (lpsa), and the dataset has 97 observations. The Variance Inflation Factor (VIF) values of the predictor variables of the dataset are 3.09, 2.97, 2.47, 2.05, 1.95, 1.37, 1.36 and 1.32, and the condition number is 243, which shows high multicollinearity among the predictor variables. Stamey et al. [15] have examined the correlation between the level of prostate specific antigen with those eight clinical measures. Further, Tibshirani [9], Efron et al. [11] and Zou and Hastie [12] have used this data to examine the performance of LASSO, LARS algorithm and Enet estimators. This data set is attached with “lasso2” R package. We have used 67 observations to fit the model, and 30 observations to calculate the RMSE. The cross-validated RMSE of the algorithms are displayed in Table 5, and Coefficient paths of each algorithm are displayed in Figure 4.
From Table 5, we can observe that LARS-rd algorithm outperforms other algorithms on Prostate Cancer Data. From Figure 4, we can observe that LARS-LASSO, LARS-EN, LARS-AURE, LARS-and LARS-AULE ignore the variables age and pgg45 in the final model, but LARS-PCRE, LARS-rk and LARS-rd ignore the variable pgg45 only.
UScrime Data: The UScrime dataset has 16 variables with 47 observations, and it is attached with “MASS” R package. This data set contains the following columns: M (percentage of males aged 14 - 24), So (indicator variable for a Southern state), Ed (mean years of schooling), Po1 (police expenditure in 1960), Po2 (police expenditure in 1959), LF (labor force participation rate), M.F (number of males per 1000 females), Pop (state population), NW (number of non-whites
![]()
Figure 4. Coefficient paths of the (a) LARS-LASSO; (b) LARS-EN; (c) LARS-AURE; (d) LARS-LE; (e) LARS-AULE; (f) LARS-PCRE; (g) LARS-rk and (h) LARS-rd versus ![]()
for the prostate cancer data.
per 1000 people), U1 (unemployment rate of urban males 14 - 24), U2 (unemployment rate of urban males 35 - 39), GDP (gross domestic product per head), Ineq (income inequality), Prob (probability of imprisonment), Time (average time served in state prisons), y (rate of crimes in a particular category per head of population). The variable y is considered as a dependent variable, and the variable So is ignored since it is categorical. Venables and Ripley [16] have
examined the effect of punishment regimes on crime rates using this dataset. The Variance Inflation Factor (VIF) values of the predictor variables of the dataset are 113.028, 104.58, 9.97, 7.43, 5.19, 5.05, 4.83, 3.84, 3.69, 2.88, 2.86, 2.75, 2.66 and 2.53, and the condition number is 923, which shows high multicollinearity among the predictor variables. For the analysis, we have used 37 observations to fit the model, and 10 observations to calculate the RMSE. The cross-validated RMSE of the algorithms are displayed in Table 6, and Coefficient paths of each algorithm are displayed in Figure 5.
From Table 6, we can observe that LARS-rd algorithm outperforms other algorithms on UScrime Data. From Figure 5, we can observe that:
• LARS-LASSO ignores the variables Ed, Ineq and Prob,
• LARS-EN, LARS-AURE, LARS-and LARS-AULE, LARS-PCRE ignore the variables Ineq and Prob, and
• LARS-rk and LARS-rd ignore the variables M, M.F and Ineq.
Since different algorithms choose the different combination of predictor variables in the final model, as shown in the plot of coefficient paths, the researcher can decide the most suitable model for the relevant practical situation.
![]()
Table 5. Cross-validated RMSE values of prostate cancer data.
![]()
Table 6. Cross-validated RMSE values of UScrime data.
![]()
Figure 5. Coefficient paths of the (a) LARS-LASSO; (b) LARS-EN; (c) LARS-AURE; (d) LARS-LE; (e) LARS-AULE; (f) LARS-PCRE; (g) LARS-rk and (h) LARS-rd versus ![]()
for the UScrime Data.
4. Conclusions
This study clearly showed that the proposed LARS-rk and LARS-rd algorithms performed well in the high dimensional linear regression model when moderated and high multicollinearity existed among the predictor variables, respectively.
The appropriate algorithm for a particular practical problem can be chosen based on the variables of interest and prediction performance by referring to the plot of coefficient paths.
Acknowledgements
We thank the Postgraduate Institute of Science, University of Peradeniya, Sri Lanka for providing all facilities to do this research, and also we thank the reviewers for their valuable comments.