Anchoring Heuristics, Investor Sentiment and Stylized Facts in the Stock Market: An Agent Based Model ()
1. Introduction
The theoretical and empirical literature in the finance area reveals that there are many stylized facts in the stock markets which require a theoretical explanation [1], but four of them stand out ( [2] - [7]):
1) The absence of linear auto-correlation on returns: (linear) auto-correlations of asset returns are often insignificant, except for very small intraday timescales (20 minutes) where microstructure effects come into play.
2) Excess volatility of the returns of single stocks or the stock index: empirical studies point to the fact that it is difficult to justify the observed level of variability in asset returns by variations in “fundamental” economic variables.
3) Heavy tails: the (unconditional) distribution of returns displays a heavy tail with positive excess kurtosis.
4) Volatility clustering: [8] argues that “large changes tend to be followed by large changes, of either sign, and small changes tend to be followed by small changes.” A quantitative manifestation of this fact is that, while returns themselves are uncorrelated, absolute returns display a positive, significant and slowly decaying autocorrelation function, ranging from a few minutes to several weeks.
There are many alternative explanations for these instances of stylized facts with or without explicit micro-fundamentals regarding the behavior of heterogeneous agents operating in a complex stock market. The Efficient Market Hypothesis (EMH) composed of representative agents with rational expectations can replicate the first stylized fact, but considers the other remaining ones to be anomalies or puzzles ( [4] and [9]). According to [10] : “Economic and finance theory is witnessing a paradigm shift from a representative agent with rational expectations to bounded rational agents with heterogeneous expectations. This shift reflects growing evidence of the theoretical limitations and empirical challenges of the traditional view of homogeneity and perfect rationality in finance and economics. The existence of limitations to fully rational behavior and the roles of psychological phenomena and behavioral factors in individuals’ decision making have been emphasized and discussed from a variety of standpoints in the economics and finance literature. Due to endogenous uncertainty about the state of the world and limits to information and computational ability, agents are prevented from forming rational forecasts and solving lifetime optimization problems. Rather, agents favor simple reasoning and ‘rules of thumb’, such as the well documented technical analysis and active trading practiced by financial market professionals. In addition, empirical investigations of financial time series show a number of market phenomena (including bubbles, crashes, short-run momentum and long-run means reverting to asset prices) and some common features, the so-called stylized facts, which are difficult to accommodate and explain within the standard paradigm based on homogeneous agents and rational expectations. Moreover, agents are heterogeneous in their beliefs and behavioral rules, which may change over time due to social interaction and evolutionary selection.”
In turn, econometric models with processes such as GARCH, FIGARCH and HAWKES applied to finance, try to explain the phenomenon of volatility clusters of stock returns by the presence of a structural break in the return time series or by non-stationary stochastic processes without providing a plausible theoretical explanation [3].
Another research line searches to reproduce the stock market stylized facts modelling the market microstructure: the stock market book of purchases and sellings, by agent-based models supposing traders bounded rationality [11]. Despite the evident theoretical and methodological contribution to the estimation parameters and the empiric validation, in this research line the representation of the investor’s behavior is not based on principles and concepts of Behavioral Economics, which certainly can contribute to improve the model’s explanation power [12].
Another promising possibility is behavioral finance theory which argues that financial phenomena can be understood using models in which some agents are not fully rational or present bounded rationality ( [13] [14] [15] and [16]). This theory focuses on two building blocks: 1) limits to arbitrage, which argues that it can be difficult for rational traders to undo the distortions caused by less rational traders; and 2) psychology, which catalogues the kinds of deviations from full rationality that we might expect to see [17]. However, there are few stock market ABMs that explicitly search to model the behavior of bounded rational agents using heuristics and behavioral biases to explain the stylized facts. The majority of the stock market ABMs search to explain stylized facts by the interaction of fundamental and chart traders with heterogeneous expectations and do not explore the role of anchoring, representative and availability heuristics and behavioral biases such as investor sentiment (excess optimism and pessimism) [10]. The formation of heterogeneous expectations by bounded rational agents under conditions of uncertainty implies a relevant role for investor sentiment in the endogenous dynamics of price formation (see [18] and [19]): excess volatility, heavy tails and volatility clustering strongly suggest that self-perpetuating effects or positive feedback loops are at play. So, despite the fact that mathematical models with processes like GARCH or HAWKES explicitly describe such feedback effects, they do not provide an understanding of its microscopic source ( [20] [21] and [22]).
In this new research line based on Behavioral Finance Theory, one strategy consists on applying the Prospect Theory to formulate agent-based models of artificial financial markets composed by bounded rational traders who suffer from disposition effect and risk aversion. The contribution of [23] to the literature is to offer a unified way to model noise traders. Regularly, agent based models in finance use different rules to model the behavior in the financial market: one for the skilled investors and other to more naïve ones. The noise traders would be included in the second group. The proposal is to model both groups with the same rule searching to replicate stylized facts, such as: clusters of volatility, negotiation volume responds to the volatility, skewness and kurtosis of returns that match with the observed ones. On the other hand, the contribution of the paper of [24] is to formulate an agent based model with a multi-asset framework when investors’ trading exhibits the disposition effect. The artificial financial market is populated with traders following two heterogeneous trading strategies: the technical and the fundamental trading rules. By simulation, the switching behavior among multiple assets is investigated, to explain important stylized facts in financial time series, such as random walk price dynamics, bubbles and crashes, fat-tailed return distributions, persistent long memory of volatility and excess volatility. Despite the advances in modelling the chart trader’s behavior, both works do not explore the effect of chart traders who adopt anchoring heuristics and suffer from attribution bias or pessimism related to their expectation about future stock prices in the aggregate dynamics of the stock market.
Another strategy, following the behavioral finance approach used in [25], it was built an agent-based model to examine the price fluctuations and the return rate dynamics in an artificial stock market under two scenarios. In Scenario 1, the focus is on the heterogeneity of the agents’ behavior with a neutral confidence level or sentiment in a market formed by 25 fundamental and 75 chart agents (25 chart agents with prices and dividend memory size = 1, 25 chart agents with memory size = 5, and 25 chart agents with memory size = 10). In scenario 2, it was used the same market configuration but varied the chart agents’ level of confidence. They found that chart agents who are confident generate higher price and rate of return volatilities than those who are not and that kurtosis and skewness are lower in their simulation study of agents who are not confident. They also showed that the stock price and confidence index are cointegrated and that stock price affects confidence index but confidence index does not affect stock price.
However, despite the theoretical advances in terms of the micro-fundamentals of the chart agents’ behavior, some limitations persist in [25]. The first is that there is little diversity of expectation formation rules, and this lack of realism in supposing that trend following chart agents make projections of price and dividends simultaneously and adjust the perceived risk of price and dividends. In the process of expectation formation, a standard behavior of trend following chart agents is to consider only price time series and not dividend ones, according to [26]. Another limitation is the lack of an explanation of the absence of linear auto-correlation on returns and volatility clustering based on the interaction of heterogeneity and the dynamics of investor sentiment.
The contribution of the present paper is to explore a complementary and alternative research strategy to model the behavior of the chart traders with bounded rationality assuming that these chart traders use an anchoring heuristics in the evaluation and stock trading decision. These agents also suffer from attribution bias/excess pessimism according to how accurate/mistaken their price expectation was. So, the objective is to improve the analysis developed about stock market through an ABM by building a market capable of simultaneously explaining three of the main stylized facts of the stock market, increasing the micro-diversity of chart agents and the realism of the expectation formation rules.
Regarding the model of [27], the number of chart agents rises from 3 to 8 groups who form their expectations through technical analysis rules which are usually applied by trend following chart agents, who do not consider or make dividend predictions. The normality test, the standard deviation of returns and the excess kurtosis tests were applied to verify the effects of heterogeneity and chart agent sentiment regarding the generation and explanation of excess volatility and the heavy tail distribution of returns, we applied. To verify the effect of chart agent sentiment regarding the generation and explanation of the volatility clustering phenomenon, the linear autocorrelation test on the logs of the returns and the absolute returns was applied.
Finally, a theoretical explanation of the stylized facts by an ABM with behavioral micro-fundamentals and the interaction of bounded rational fundamental and chart agents can promote the formation of methodologies for price predictions and the risk assessment of buying and selling operations of shares used by institutional, chart and noise trader investors ( [26] [28] and [12]).
This study is organized as follows: Section Two describes the model framework and how agent expectations are determined, Section Three analyzes, through econometric tests, the role of expectations and sentiments of trend following chart agents’ heterogeneity in the generation of stylized facts and Section Four presents our final considerations.
2. The ABM of the Artificial Stock Market
2.1. Model Framework
The artificial stock market used in the study described in this paper is composed of 224 agents, varying between homogeneous rational expectation fundamental agents or traders (who represent the EMH) and heterogeneously bounded rational expectation chart agents or traders (who represent behavioral finance). The fundamental traders make their market price forecast using the discounted present value method of the future flow of dividends, supposing that the market price of shares will inexorably converge on the fundamental price; while the chart traders make their expectations of prices based on the anchoring heuristic and are also trend followers.
Agents can’t change their strategy, so the number of agents following a specific strategy is predetermined ( [25] and [27]). The chart agents are divided based on their choice of analysis indicators used to arrive at their price expectations. The indicators used are: max and min; simple moving average (SMA) and exponential smoothing (ES). As a result of their choices, agents check whether the effective price at t is higher than the expected price at t, and check whether the result was positive or negative (In Scenario 3, the sentiments of the investors or their levels of confidence in their predicting power are included).
There are three scenarios:
Scenario 1: all of the 224 agents or traders are homogeneous, and use fundamentals with rational expectations.
Scenario 2: there are interactions between fundamental and chart traders that establish the stock market price. However, the sentiments of these agents in situations of price prediction success or failure remain unaltered: there is no attribution bias, excess confidence or decrease in the confidence level. Among the chart agents, the price expectations are built with 8 different type of memories, divided into 10, 20 and 30 cycles, according to previous research on the same theme (similar to [29]):
• Max price of the last 30 cycles
• Min price of the last 30 cycles
• Simple moving average of the last 10 cycles
• Simple moving average of the last 20 cycles
• Simple moving average of the last 30 cycles
• Exponential smoothing of the last 10 cycles
• Exponential smoothing of the last 20 cycles
• Exponential smoothing of the last 30 cycles
Scenario 3: the chart agents have heterogeneous expectations as in Scenario 2, however their behavior sentiment is different: there is attribution bias or excess self-confidence if the predictions are successful and a decrease in their self-confidence level if the price predictions are wrong.
All agents must choose between two assets to invest: 1) a riskless asset that has a constant interest rate (r) with an infinite elastic supply (r), and 2) a risky asset that pays a stochastic dividend that follows a first order autoregressive process AR(1).
Time is discrete and indexed by t with a total of 5000 cycles. The stock market price set at time t is made considering supply and demand. With the setting of the stock market price at time t, the portfolio of all agents is updated as well as their wealth level at the current time. The individual behavior of the agents generates series that are stored to make further analyses.
There is a restriction on the amount of stock that can be acquired by agents, so each agent can demand no more than 5 stocks in each cycle. Also, only a maximum of 5 stocks may be short-sold. The amount of stocks traded by the agents is restricted by the amount of resources they have available to buy.
The formal structure of the artificial stock market considers four global variables: 1) Dividends; 2) Financial Resources; 3) Demand and 4) Price.
For the dividend variable, the current dividend (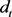
) paid by a risky asset (stock) in each cycle (time t) is calculated by an exogenous first order stochastic process AR(1) (similar to [5] [25] and [27]):
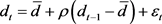.(1)
where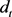
: current dividend;
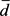: initial dividend;
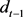: previous dividend;
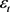: follows a normal distribution with an average of 0 and finite variance 
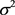and
.
Similarly, for the Financial Resources variable the agents are assumed to have the same utility function. More specifically, the agents have constant absolute risk aversion (CARA). Each agent tries to maximize its allocation between risky assets (the amount of shares) and riskless assets without interest (money). In each cycle everybody tries to maximize the expected utility of their wealth (as in [27] [30]):
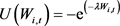.(2)
where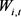
: wealth of agent i at t and
: relative risk aversion level of agents.
Each agent i has the same initial value of wealth (
) and can accumulate wealth through investments. So, at time t, each agent has two ways of keeping his or her wealth:
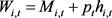.(3)
where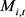
: is money and
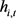: are shares.
In the remaining amount of time, the financial resources available for investments will be:
.(4)
where 
represents wealth of agent i at t,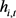
: are shares demanded by agent i at t,![]()
: price at t,![]()
: share dividend at t and r: represents the interest rate of the riskless asset (money).
For the demand variable, the maximization of expected utility of agent i is represented by:
![]()
.(5)
subject to:
![]()
.(6)
For the fundamental agent, the optimum amount of shares demanded at time t will be proportional to the difference between the agents’ homogeneous expectations of price and dividend during the next period and the actual price accrued by the interest rate (r) and inversely proportional to the measure of the absolute risk aversion (![]()
) and the perceived variance of returns (![]()
).
![]()
.(7)
where![]()
: is the perceived variance of returns, considering the price and dividend volatility. The perceived variance of returns which is the same as the effective variance of fundamental traders (![]()
) is calculated as in [27] :
![]()
.(8)
where parameter ![]()
is the weight placed on the most recent squared errors as opposed to the weight of past squared errors. This parameter is important because the more weight the agents give to recent deviations, the more volatile and susceptible to noise their trades will be.
For the chart agent, the optimum amount of shares demanded in time t will be proportional to the difference between the agent’s expectations of the price in the next cycle and the current price accrued by interest rate r and inversely proportional to the absolute risk aversion (![]()
) and the perceived variance of returns (![]()
).
![]()
.(9)
where ![]()
is the perceived variance of returns considering only the share price volatility which is determined by the self-confidence level ![]()
(Equation (22)) and the actual variance of:
![]()
.(10)
For the Price variable we considered the optimum amount of shares demanded![]()
. The artificial market functioning (as in [30]) is described by two behaviors. If the amount demanded by agent i was greater than or equal to that of the previous cycle, then he or she buys the difference:
![]()
.(11)
And, if the amount demanded by agent i was less than that of the previous cycle, then he or she sells the difference:
![]()
.(12)
This way, the total amount of the purchase and sale will be given by:
![]()
.(13)
![]()
.(14)
where ![]()
is the total amount of buy orders; ![]()
is the total amount of sell orders and N is the number of agents.
So, the risky asset market price will adjust itself in terms of supply and demand:
![]()
.(15)
According to [31], ![]()
can be interpreted as the speed of the price adjustment, representing a scale factor that normalizes the excess demand in the stock market and is considered to be a factor that eases market fluctuations.
2.2. The Formation of Expectations for Fundamental Agents
Based on the models of [25] [27] and [32], we considered that fundamental agents form rational expectations of future share prices based on the model of discounted future dividend flow or the [33] model by considering the probability distribution of dividends and assuming a constant increase rate of g:
1) Future dividends expectation:
![]()
.(16)
where ![]()
is the dividend payed by the shares at the current time and g is the expected constant increase rate of the dividend.
2) Future stock price:
![]()
.(17)
where k is the discount factor that the market demands for these shares.
From Equation (16) and Equation (17), the fundamental trader forms his or her expectations of the share price and the dividend: ![]()
that will take place in the definition of the optimum amount of shares for each agent i in each cycle: the fundamental agent or trader will make arbitrage buy (sell) operations if the current market price is less (greater) than the fundamental price predicted.
2.3. Heterogeneous Formation of Expectations by Chart Agents Based on Anchoring Heuristics and Investor Sentiment
Chart agents will form their expectations considering only the price and will not make estimations of dividends. Also, they do not account for the fundamental price of shares. The technical analysis uses volume data along with price history to drive the trade strategy ( [26] [34]). The anchoring of chart agents’ expectations is performed over the indicators already described: Max and Min, Simple Moving Average and Exponential Moving Average.
The expectations regarding the future price when the max price rule is used is:
![]()
.(18)
where ![]()
is the number of cycles considered in the calculation of the max price. This specification of the time horizon is found in [29].
Likewise, the expectations regarding the future price when the min price rule is used is:
![]()
.(19)
where n is the number of cycles considered in the calculation of the min price. This calculation assumes only that ![]()
cycles.
Furthermore, the expectation about the future price when a chart trader uses the simple moving average rule is:
![]()
.(20)
where n is the number of past prices considered in the calculation of the average price. There are also three types of chart traders using this calculation rule:![]()
, ![]()
and![]()
.
Finally, the expectations regarding the future price when a chart trader uses the exponential smoothing rule is:
![]()
.(21)
where Smooth is the exponential smoothing of prices. There are also three types of chart traders using this calculation rule:![]()
, ![]()
and![]()
.
According to the Behavioral Finance theory, the evaluation process and financial decisions during uncertainty are based on anchoring, representative and availability heuristics and on investor sentiment and intuition ( [17] and [35]). This paper assumes that bounded rational chart traders during periods of uncertainty build their expectations regarding prices using anchoring heuristics. However, since they are susceptible to making systematic errors in judgement, chart traders should compare their expectations about prices at time t with actual prices at time t: if the predicted price error falls between an estimated confidence interval, the level of self-confidence increases, while if the predicted price error falls outside of the same interval, there is a decrease in the confidence in their prediction power.
According to [32], to model the chart traders’ sentiment dynamics in Scenario 3, described in Section 3, we use the actual variance of the stock returns as in Equation (10) and create a confidence interval (C) that, when multiplied by the actual variance of stock returns, should characterize the underestimation or overestimation of perceived risk:
![]()
.(22)
where coefficient ![]()
represents the confidence level of the chart trader in regard to his or her expectations. When![]()
, the agent has a neutral confidence level and the variance of stock returns cannot be either overestimated or underestimated. When![]()
, the agent is overconfident and the variance of the return is underestimated. When![]()
, the agent lacks confidence and the variance of the stock return is overestimated.
The level of agent confidence, ![]()
, is updated based on the success or failure of their predictions. We carry out this updating by first mapping the confidence coefficient ![]()
from interval ![]()
into a more limited interval, ![]()
, as described by [32]. After that transformation, the levels of confidence are updated according to:
![]()
.(23)
where ![]()
corresponds to the perceived standard deviation of the stock return. If the difference between the expected stock return and the actual return is within the interval of confidence, then the level of confidence (![]()
) will be increased by parameter![]()
. If it is not, the agents are less confident and ![]()
is multiplied by parameter![]()
. It is possible that the updating of the level of agent confidence is biased, since the increase in confidence level for good predictions can be greater than the decrease in confidence level for bad predictions. This paper assumes that a non-biased self-attribution bias occurs. After the level of agent confidence is updated, ![]()
is mapped at the original interval ![]()
using the inverse transformation function used by [32].
3. Analysis of the Results
To analyze the capability of the artificial stock market ABM to generate and explain these stock market stylized facts, we have prepared three scenarios:
1) In Scenario 1, the stock market is formed by 224 (100%) fundamental traders with homogeneous rational expectations.
2) In Scenario 2, the stock market consists of 75% (168) fundamental traders and 25% (56) trend following chart traders who form their expectations of share prices through anchoring heuristics and do not present adaptive behavioral sentiments: 7 chart traders use the max price rule of 30 cycles, 7 chart traders use the min price rule of 30 cycles, 21 chart traders use the simple moving average of 10, 20 and 30 cycles (7 chart traders in each rule) and 21 chart traders use the exponential smoothing of 10, 20 and 30 cycles (7 chart traders in each rule).
3) In Scenario 3, the market configuration is the same as that of Scenario 2. The only difference is that, in this scenario, chart traders with heterogeneous expectations also present behavioral sentiments that adapt with the successes and failures of their market price predictions.
The initial conditions and parameter values are reported in Table 1. To verify the effect of the heterogeneity of expectations in Scenario 2, the percentage of chart traders is increased to 25%. To evaluate the effect of investors’ sentiment adaptation (attribution bias and pessimism) with the success or failure of their predictions in Scenario 3, for the 25% of the trend following chart traders, the parameter that captures the attribution bias is reduced to 0.93, while the parameter that captures the pessimist feeling is increased to 1.07.
Econometric Analysis: EMH and Behavioral Finance
The simulation results of Scenario 1, in which the market is 100% formed by homogeneous agents with rational expectations are:
1) the return is the log value of shares and follows a normal distribution, with significance levels of 1% and 5% (Table 2, Figure 1);
2) there is no excess volatility of share returns in the log: the standard deviation of share prices (0.09232) is relatively close to the standard deviation of dividends (0.04572) (Table 2 and Figure 2);
3) the return is the log value, which is stationary and the linear autocorrelation of the log value of the returns decays quickly, becoming non-significant in small lags (Table 3 and Figure 3);
4) the absolute return is the log value and is stationary and does not present a long memory: the autocorrelation of absolute returns decays quickly to zero.
![]()
Table 1. Initial conditions and general parameters.
Source: Prepared by the Authors based on [27] with small changes.
![]()
Table 2. Descriptive statistics of scenarios.
Source: Prepared by the Authors. aThe excess Kurtosis of Scenario 3 is closest to the S&P 500 index which presents excess Kurtosis of about K = 16 as in [2].
![]()
Table 3. Unit root tests of returns and absolute returns.
Source: Prepared by the Authors.
![]()
Figure 1. Distribution of share returns under three scenarios.
![]()
Figure 2. Volatility of returns of shares under three scenarios.
![]()
Figure 3. Linear autocorrelation of share returns under three scenarios.
Therefore, in the absence of linear autocorrelation, the return is the log value (Figures 3-5).
![]()
Figure 4. Volatility of absolute share returns under three scenarios.
![]()
Figure 5. Linear autocorrelation of absolute share returns under three scenarios.
As it is possible to observe, the results obtained in Scenario 1 are those supported by the EMH, with the presence of only one stylized fact: the absence of linear auto-correlation on returns.
The simulation of the three scenarios generated distributions of returns that are very different, as it is possible to see in Figure 1.
Figure 2 and Figure 4, shows that the time evolution containing a sub-set of 5000 values for the returns are the log values (r) and the absolute returns (![]()
), respectively, suggesting a stationarity behavior in all cases.
One of the requirements in validating linear autocorrelation tests of returns are the log values and absolute returns consider the hypothesis that the stochastic process is stationary ( [2] and [3]). Indeed, the hypotheses were first tested for the time series describing random walks: 1) returns are the log values of shares and 2) absolute returns of shares, using the following unit root tests: a) Phillips-Perron Test; b) Augmented Dickey-Fuller Test; and c) Kwiatkowski-Phillips-Schmidt-Shin (KPSS) (Table 3).
All four unit root tests corroborate the results shown in Figure 2 and use a base significance level of 5% (p-value < 0.05), as shown by the values in Table 3. Thus the results for returns and absolute returns show that we can reject the null hypothesis in the Phillips-Perron and Augmented Dickey-Fuller Tests and we cannot reject the null hypothesis in the KPSS test, thus all the series do not have a unit root and are stationary, at a significance level of 5%.
The absence of linear auto-correlation on returns is an expected result by the EMH. The linear auto-correlations of share returns under three Scenarios are shown in Figure 3, where Series ACF1, Series ACF2 and Series ACF3 refer to Scenario 1, 2 and 3, respectively.
Empirical studies have pointed to excess volatility of the returns that are difficult to justify by variations in “fundamental” economic variables. Figure 4 shows the volatility of absolute share returns in 5000 cycles, where Ab1, Ab2 and Ab3 represent the three Scenarios, respectively.
According to stylized fact known as volatility cluster, while returns themselves are uncorrelated, absolute returns display a positive, significant and slowly decaying autocorrelation function. The linear autocorrelation of share returns is shown in Figure 5, where the ACF1, ACF2 and ACF3 refer to Scenario 1, 2 and 3, respectively.
In addition, the emergent proprieties of Scenario 2, in which trend following chart agents have heterogeneous expectations regarding market prices, are:
1) the returns are the log values and they do not follow a normal distribution, but also do not present heavy tail or positive excess Kurtosis (1.7748) (Table 2 and Figure 1);
2) there is excess volatility of share returns in the log value: the standard deviation of share prices (0.595) is much higher than the standard deviation of dividends (Table 2 and Figure 2);
3) the return is the log value and is stationary, and the linear autocorrelation of the return is the log value, and is significant for large lags (Table 3 and Figure 3);
4) the absolute share return is the log value and is stationary and has positive and negative long memory: the linear autocorrelation of absolute returns is significant at a level of 5%, but presents positive and negative values. Therefore, in Scenario 2, only one stylized fact is explained: the excess volatility of prices and share returns due to the presence of heterogeneous expectations of trend following chart agents who deviate market prices from the fundamental prices (Figures 3-5).
Finally, under Scenario 3, the interaction of traders with heterogeneous expectations and with adaptive behavioral sentiments generates and explains the following emergent properties:
1) the distribution of share returns in a log value presents a heavy tail and positive excess Kurtosis (18.5615) (Table 2 and Figure 1);
2) there is excess volatility in share prices (0.2145) in relation to their fundamental dividend (0.04572) (Table 2 and Figure 2);
3) the linear autocorrelation of absolute share returns in a log value decays slowly to zero revealing the presence of long memory and nonlinear dependence. This way, it signals the phenomenon of volatility clustering: small returns are followed by small returns while large returns are followed by large returns (Table 3; Figures 2-5).
To sum up, in Scenario 1, the artificial stock market is composed by 100% of fundamental traders with rational and homogeneous expectation who do not suffer from attribution bias or excess pessimism. Additionally, this scenario is capable to reproduce only one stock market stylized fact: the absence of linear auto-correlation on returns for small lags. In scenario 2, however, the stock market is populated by 75% of fundamental traders with rational and homogeneous expectation and by 25% of chart traders that in their stock trade evaluation and decision processes adopt the anchoring heuristic but do not suffer from attribution bias and excess pessimism. Also, in this Scenario 2, as a result from the interaction among fundamental and chart traders, only one stylized fact emerges: the excess volatility of prices and share returns due to the presence of heterogeneous expectations of trend following chart agents who deviate market prices from the fundamental prices. At last, in Scenario 3, the composition of fundamental and chart traders is the same as in Scenario 2. However, in this Scenario, chart traders can suffer from attribution bias and excess pessimism related to their future price expectation. The interaction of traders with heterogeneous expectations and with adaptive behavioral sentiments generates and explains the following emergent properties: 1) the distribution of share returns in a log value presents a heavy tail; 2) the excess volatility in share prices in relation to their fundamental dividend; 3) the linear autocorrelation of returns in log decays quickly to zero; and 4) the linear autocorrelation of absolute share returns in a log value decays slowly to zero revealing the presence of long memory.
4. Conclusions
This paper searches to show that there are many complementary and alternative theoretical and methodological approaches to describe and explain the stock market’s stylized facts and, at the same time, proposes another approach based on Behavioral Finance Theory. Section 3 searches to explore the empirical implications of the proposed theoretical and methodological approach by the simulation of the emergent proprieties of an artificial financial market.
In this paper, a stylized stock market ABM formed by two types of traders was constructed. The first type, inspired by the EMH theoretical literature, consists on fundamental traders with homogeneous rational expectations that perform arbitrage operations seeking to exploit deviations of the stock price from its fundamental value. The second type of agent, inspired by the Behavioral Finance theoretical literature, consists on trend following chart traders that, in the formulation of expectations about share prices under conditions of uncertainty or complexity, use the anchoring heuristic and have variable behavioral sentiments: they suffer from self-attribution bias (excess self-confidence) when their predictions are successful and a decrease in self-confidence when their predictions fail.
Another theoretical contribution is that the stylized stock market ABM is capable of explaining four of the main stylized facts of the stock market for daily frequency.
The results of simulations in Scenario 1 in which 100% are fundamental agents show that arbitrage operations by fundamental agents generate (explain) the absence of autocorrelation for small lags on the return in log values, which is consistent with the EMH; but does not generate (explain) the excess volatility, heavy tail or leptokurtic distributions and the volatility clustering of stock returns in log values.
Under Scenario 2, with 75% fundamental agents and 25% trend following chart agents with fixed behavioral sentiments, it is possible to verify the emergence of excess volatility of share returns in log values. However, despite the interaction between fundamental agents with homogeneous rational expectations and chart traders with heterogeneous expectations being the reason for the emergence of excess volatility, it still isn’t able to explain the other two stylized facts of returns in log values: heavy tail distribution with positive Kurtosis and the volatility clustering characterized by long memory.
Finally, under Scenario 3, it is possible to observe that the interaction between fundamental traders and chart traders with heterogeneous expectations and variable behavioral sentiments explain the emergence of three stylized facts of the stock market: 1) the excess volatility of share returns in log values, 2) the heavy tail distribution with positive Kurtosis on returns in log values and 3) volatility clustering characterized by the presence of the positive and significant autocorrelation of absolute returns for large lags or the presence of long memory. The absence of linear autocorrelation of returns in log values for large lags, and at the same time the presence of positive and significant autocorrelation of absolute returns for large lags, imply that there should be a nonlinear and long memory dependence in the share returns. “The volatility clustering feature indicates that asset returns are not independent across time; on the other hand, the absence of linear autocorrelation shows that their dependence is nonlinear” [3].
In short, in this paper argues that the presence and interaction of heterogeneous expectations and the adaptive sentiments of trend following chart traders are essential ingredients to explaining and justifying the emergence of three of the main stylized facts considered to be stock market puzzles by the EMH: excess volatility, heavy tail distributions and the long-term memory of share returns. Future work can extend the findings of this paper to increase the effectiveness of technical analysis predictions of share prices. Also, it is possible to model chart agents who operate against the trend to see their impact on the artificial stock market.