Robust Estimation of the Normal-Distribution Parameters by Use of Structural Partitioning-Perobls D Method ()
1. Introduction and History of Robust Estimation
The history of this problem is older than 300 years. For example, Galileo as long ago as in 1632 used the least absolute sum in order to reduce the effect of observational errors to the estimate of the measured quantity [3], whereas Rudjer Boscovich, is the first who, as early as in 1757, rejected clearly outlying observations [4], also done by Daniel Bernouli 1777 [4]. The trimmed mean has been used since long ago, see “Anonymous” 1821 [4]. The first formal rules for rejecting of observations were proposed by Peirce 1852 and Chauvenet 1863, and somewhat later appear the papers by Stone 1868, Wright 1884, Irvin 1925, Student 1927, Thompson 1935, and by many others [4].
The mixed distribution models have been also considered since long ago: Glaisher 1872/1873, Stone 1873, Edgeworth 1883, Newcomb 1886, Jeffreys 1932/1939 [4]. Tukey in 1960 [5] defined a mixed model as a mixture of two normal distributions of a basic
and of a contaminating
distribution:
,
where
is the function of the standard normal
distribution. Here the elements of the contaminating set appear with probability
, (Tukey assumes
as a small number, about 5%), and behave as gross errors. In this way the real distributions are represented through a normal-distribution model with weighted tails.
The term robustness began to be used since 1953 (introduced by G. E. P. Box) in order to discriminate the class of statistical procedures with little sensitivity to minor deviations from the starting assumptions. Some authors use the term stability, but it is less used than the term robustness. In the Foreword of his book ROBUST STATISTICS, Huber in 1981 [6] emphasizes that among the leading scientists in the late XIX and the early XX centuries there were a few statisticians—practitioners (and mentions: astronomer Newcomb, astrophysicist Eddington and geophysicist Jeffreys) who expressed in their studies a perfectly clear understanding of the robustness idea. They were aware of the perils caused by long tails of the functions of error distributions, so they proposed models of distribution of gross errors and derived robust variants of standard estimates. Russian geodesists, for example, in their adjustments of the first order triangulation networks allowed lower weights (about half of the original ones) to the observations of directions which do not deviate much.
The initial fundaments to the theory of robust estimation were laid by Swiss mathematician P. J. Huber 1964 [1] and American statistician W. J. Tukey 1960 [5]. Huber’s article “Robust Estimation of Location Parameter” was the first fundament of the theory of robust estimation, which introduced an elastic class of estimates, called M-estimates, which have become a very useful instrument, having established which properties they have (for instance consistency and asymptotic normality). He introduced the model of gross errors, replacing the strict parametric model
, with its known distribution F, by the mixed model:
,
while a part of data
(
) may contain gross errors which have an arbitrary (unknown) distribution
.
The causes of deviating from the parametric models are various and four main types of deviating from the strict parametric models can be distinguished:
1) Appearance of gross errors;
2) Rounding and grouping;
3) Using an approximate functional mode; and
4) Using an approximate stochastic model.
The fundamentals of robust methods were developed in the last century. Today there are numerous applications of robust methods, and concurrently better and more detailed solutions are sought: [2] [7] - [14].
Due to good properties of the robust methods—that it is possible to eliminate or decrease the influences of gross errors and outliers on the estimates of distribution parameters, in practice they are used more and more. Therefore, the same time, their development results. So the current development and application of the robust methods may be classified into the following groups:
➢ Improvement of existing methods, such as “A new Perspective on Robust M. Estimation” [13];
➢ Solving of delicate (specific) tasks:—for robust hybrid state estimation with unknown measurement noise statistics [14] —for optimal allocation of shares in a financial portfolio [8] —for robust estimation of 3D human poses from a single image [12] —for cubature Kalman filter for dynamic state estimation of synchronous machines under unknown measurement noise statistics [9];
➢ Applications in various conditions:—for robust estimation of the sample mean variance for Gaussian processes with long-range dependence [2] —for robust estimation of 3D human poses from a single image [12] —for robust hybrid state estimation with unknown measurement noise [14] —for estimation of mean and variance using environmental data sets with below detection limit observations [10];
➢ Applications in diverse fields:—for estimation of the sample mean variance for Gaussian processes with long-range dependence [2] —for Gaussian sum filtering with unknown noise statistics: Application to target tracking [11] —robust cubature Kalman filter for dynamic state estimation of synchronous machines under unknown measurement noise statistics [9] —for estimation of mean and variance in Fisheries [7] —for optimal allocation of shares in a financial portfolio [8] —for estimation of mean and variance using environmental data sets with below detection limit observations [10].
The proposed PEROBLS D method is aimed at eliminating the influences of gross errors and outliers on the estimates of distribution parameters, when only one contaminating distribution is present, i.e. in the case of Tukey’s mixed distribution.
The key difference between this paper and existing studies is that the PEROBLS D method in the estimating procedure uses no distribution censoring, unlike the existing methods, but instead a structural decomposition into two distributions is used—basic and contaminating ones which have the same mean value and then the parameters of both distributions are estimated.
Consequently, in the case that both distributions (basic and contaminating) are normal, the PEROBLS D method has the following properties:
1) Unbiased (exact) parameter estimates for the basic distribution, as the most important property;
2) Unbiased (exact) parameter estimates for the contaminating distribution;
3) Percentage estimates for fractions of basic and contaminating distributions in the mixed one.
The correctness of the method has been verified on exact (expected) values of some quantities from the mixed Tukeyan distribution, as well as on an example of simulated data for 200 measurements of one quantity.
Besides, the estimates of the mean and variance for the basic distribution have been compared with the same ones obtained by ML method, and the estimate basic distribution standard has been also compared with Tukey mad standard estimate.
As has been said, the PEROBLS D estimates are unbiased, whereas the estimates of the basic distriburion standard in both cases, according to ML and Tukey mad, are increased.
The structure of the further presentation is the following. At first definitions and notations are given, then basis of PEROBLS D method and the way of solving the formulated problem. Afterwards the existing robust estimation methods—ML and Huber’s mad—are presented. Further on the PEROBLS D method is verified on examples and the solutions are compared with existing ones. Finally, there are conclusions and references.
2. Definitions and Notations
The density function for a standard normal variable Z is given as
,
.
Let
be the notation of the distribution function for Z. The quintiles of Z will be denoted as
, where
is the significance level,
and
.
A normally distributed r. v. X with expectation
and variance
has the density and distribution functions, respectively:
and
, with
. (1)
Let as consider a random variable (natural sequence of measurements) [15] :
, from a normal population and use
, with mean
and standard deviation
, (i.e. variance
) where one assumes that the observations
are mutually independent. Arranging them in the ascending order of magnitude one obtains order statistics
(Figure 1), where the points A and B defined in the following way:
and
, (2)
where d is the width of the rounding interval for observations X.
With z from Equation (1), it will be analogously:
,
;
,
where
.
3. Basis of PEROBLS D Method1
The idea of PEROBLS D method has been presented in the Least Squares book [16].
Instead of assuming the presence of gross errors in the observations within X and Z regions, used in the previous methods, in this method the observation distribution is defined by means of Tukeyan mixed distribution (Figure 2):
, (3)
where
is the basic,
—the contaminating one, whereas
, noting that
cannot exceed 0.5, because, in this case
must be taken as the basic distribution. (In geodetic applications there is mostly
).
In this method the points A and B are partition points only, i. e. they are neither truncation points nor censoring ones. They are chosen so that in the domains X and Z the contaminating distribution prevails—which is one of the prerequisites to find a good (satisfactory) solution of the problem (task).
Note 1. In geodetic measurements distributions close to the Tukeyan ones are frequent. ▲
The designations concerning the basic and the contaminating distributions are given in Table 1.
The task is to estimate the parameters of both distributions, of basic and contaminating ones.
4. PEROBLS D Solution
The parameter estimators for both distributions will be derived from the maximal probability of the event:
where
,
,
, etc.
![]()
Figure 2. Tukeyan mixed distribution of normally distributed observations.
![]()
Table 1. Designations and terms of the quantities appearing in the basic and the contaminating distributions.
Let
(4)
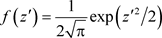 ,
,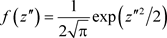 .
.
Then the likelihood function, up to the proportionality constant k, is:
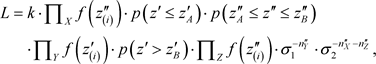
where X, Y and Z under product sign mean: , etc., and where:
, etc., and where:
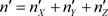 ,
, 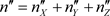 ,
, .
.
If we also introduce the notations
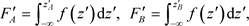

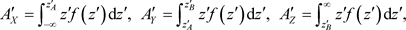
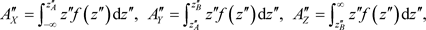
![]()
![]()
![]()
![]()
![]()
![]()
then the conditions![]() ,
, ![]() and
and ![]() yield the equations:
yield the equations:
![]() (5)
(5)
solvable only iteratively. There are many methods; here direct iterations are given.
However, within system (5), except![]() ,
, ![]() and
and![]() , the sums
, the sums![]() ,
, ![]() ,
, ![]() ,
, ![]() and
and![]() , and the numbers
, and the numbers ![]() and
and ![]() are also
are also
unknown and they should be previously determined.
For the purpose of determining ![]() and
and ![]() there are many ways. The present author has examined a few methods out of which he has adopted the least-square one. With three relationships:
there are many ways. The present author has examined a few methods out of which he has adopted the least-square one. With three relationships:
![]() (6)
(6)
where ![]() and
and ![]() are the corrections to the “observations”
are the corrections to the “observations” ![]() and n,
and n, ![]() , first using LS with assuming the “observation” weights:
, first using LS with assuming the “observation” weights: ![]() and
and![]() , we find the LS estimates for
, we find the LS estimates for ![]() and
and![]() :
:
![]() ,
, ![]() , with
, with
![]()
and then
![]() and
and ![]() with
with![]() .
.
In this way the condition ![]() is satisfied, but the conditions:
is satisfied, but the conditions: ![]() ,
, ![]() and
and ![]() are not satisfied. However, since all conditions in Equations (6) cannot be satisfied simultaneously, a compromise yielding a solution close to the optimum must be accepted.
are not satisfied. However, since all conditions in Equations (6) cannot be satisfied simultaneously, a compromise yielding a solution close to the optimum must be accepted.
The sums![]() ,
, ![]() , etc., can be also solved in various ways, but the present author has chosen the following one. At first we find the sums:
, etc., can be also solved in various ways, but the present author has chosen the following one. At first we find the sums:
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
and then by means the asymptotic theory according to which:
![]() ,
,
![]() ,
,
etc., it follows:
![]() ,
,
![]() ,
,
one introduces the substitutions:
![]()
![]()
![]()
where:
![]()
Using these results the solution of system (5) we have:
![]() (7)
(7)
![]() (8)
(8)
![]() (9)
(9)
where:![]() ,
, ![]() ,
,![]() .
.
Let ![]() be the vector of parameter estimates in the k-th iteration and d the difference vector of these estimates from (k+1)-th and k-th iterations, then the iterations should be stopped if
be the vector of parameter estimates in the k-th iteration and d the difference vector of these estimates from (k+1)-th and k-th iterations, then the iterations should be stopped if
![]()
The points of optimal partition, ![]() and
and![]() , with
, with![]() , are found from the condition
, are found from the condition![]() , where
, where ![]() and
and![]() . So one obtains:
. So one obtains:
![]() (10)
(10)
The advantages of the method are:
1) Unbiased estimators for![]() ,
, ![]() and
and![]() , if assumptions (4) hold and A and B are close to
, if assumptions (4) hold and A and B are close to ![]() and
and![]() ; and
; and
2) Minimal variances for![]() ,
,![]() .
.
The disadvantages of the method are:
1) A high sensitivity to the choice of the points A and B, (points A and B must be close to ![]() and
and![]() ), which can result in negative estimates for either of the variances
), which can result in negative estimates for either of the variances ![]() or
or![]() , or for both; and
, or for both; and
2) Sensitivity to the choice of the initial values for the variances ![]() and
and![]() , which, also, can result in negative estimates for one or both variances.
, which, also, can result in negative estimates for one or both variances.
Therefore, the method is recommendable for applications comprising a high number of observations, (for example![]() ).
).
Note 2. If there exists the basic distribution only (when in Equation (3)![]() ), the method will yield either
), the method will yield either ![]() or negative values for one or both variances.
or negative values for one or both variances.
5. Some Robust Estimation
Out of many robust LS methods we shall use here two of them: the method of Maximum Likelihood (ML) and Huber's mad estimation of distribution standard [6] [17].
5.1. The Maximum Likelihood (ML) Method
The ML method is based on the assumption that in the domain Y there exists only the basic distribution, unlike the domaines X and Z where in addition to the basic distribution there exist gross errors and outliers. Here the censoring points are A and B and they are defined according to Equation (2).
In the region (![]() ), due to the presence of gross errors in the observations, the distribution of the random variable X is not normal. Therefore, the estimates of the parameters
), due to the presence of gross errors in the observations, the distribution of the random variable X is not normal. Therefore, the estimates of the parameters![]() , and
, and ![]() are determined on the basis of the probability of the event:
are determined on the basis of the probability of the event:
![]() ,
,
where the events![]() ,
, ![]() , mean that the random variable X is within an interval
, mean that the random variable X is within an interval ![]() (with differentially small
(with differentially small![]() ).
).
Then the likelihood function, up to the proportionality constant, is [18] :
![]() ,
,
and the ML estimators are the solutions of the equations
![]() ,
,![]() .
.![]() , and
, and![]() . (11)
. (11)
Equations (11) have no analytical solution and they must be solved iteratively. There are several methods; here direct iterations are given:
![]() , (12)
, (12)
![]() , (13)
, (13)
where:
![]()
![]()
As initial values we can adopt![]() , and
, and![]() .
.
In the present author’s opinion under the preposition of existing of contaminating distribution the method yields increased estimates for![]() .
.
5.2. Huber’s Mad Robust Estimation of Distribution Standard
For the purpose of estimating an unknown standard ![]() Huber 1981 [6] and Birch and Mayers 1982 [17] proposed a median estimator for
Huber 1981 [6] and Birch and Mayers 1982 [17] proposed a median estimator for![]() :
:
![]() ,
,![]() . (14)
. (14)
6. Results and Discussion
Example 1. For the sake of verifying the correctness of PEROBLS D method and examining the appropriateness of Maximum Likelihood (ML) method in Table 2 are presented the exact (expected) values of some quantities from the mixed Tukeyan distribution (3), with![]() ,
, ![]()
![]() ,
, ![]() ,
, ![]() ,
, ![]() and symmetrical partitioning (
and symmetrical partitioning (![]() ). The numbers
). The numbers![]() ,
, ![]() and
and ![]() and the other quantities in the table are presentd for the case
and the other quantities in the table are presentd for the case ![]() .
.
According to data in Table 2, for two methods—PEROBLS D and ML—the estimates for the corresponding quintiles are calculated and presented in Table 3. The results of estimating the variance ![]() of the basic distribution by using ML methods indicate their appropriateness.
of the basic distribution by using ML methods indicate their appropriateness.
Example 2. Simulated Data. Using normally distributed N(0, 1) random numbers from Tables of Bol’shev and Smirnov 1968 [19] the mixed Tukeyan distribution (3) is found (Table 4), with normal distributions: basic ![]() with
with ![]() and contaminating
and contaminating ![]() with
with![]() , (
, (![]() ); with estimates:
); with estimates:
basic:![]() ,
, ![]() ,
,
contaminating:![]() ,
,![]() .
.
According to Equation (10), for ![]() and
and![]() , the optimal partition points are:
, the optimal partition points are:
![]()
for which one obtains 6.5 percent partition with ![]() and
and![]() .
.
![]()
Table 3. The results of Estimating the Normal-Distribution Parameters by using PEROBLS D, and ML methods according to the exact (expected) values of the corresponding sums given in Table 2.
In Table 5, for various choices of the partition points A and B, a survey of the parameter estimates for the basic and contaminating distributions obtained by different methods is given. The parameter estimates in the PEROBLS D method are close to the exact ones, whereas in the case of application of the ML and Huber-mad methods the variance of the basic distribution is overestimated.
The best way is to choose the partition points A and B for the PEROBLS D method from the frequency histogram (see Figure 3) by accepting the x values for which it, to the left and right of the distribution centre, begins to have values above the smoothing curve for the normal distribution.
Recommendation. The estimate of standard![]() , for the purpose of drawing the smoothing curve can be calculated according to the standard formula,
, for the purpose of drawing the smoothing curve can be calculated according to the standard formula, ![]() where 2% - 5% rejected outlying observations not taken into account. ▲
where 2% - 5% rejected outlying observations not taken into account. ▲
7. Conclusions
On the basis of the obtained results in Examples 1 and 2 we can conclude the following:
1) On the basis of exact (expected) values from Example 1 the validity of the PEROBLS D method in the parameter estimation (expectation and variance) for both distributions in the Tukeyian mixed distribution of observations is confirmed. Here the variance estimates for both distributions, basic and contaminating ones, are correct, i.e. their values are exact.
2) On the basis of simulated realistic measurements from Example 2 good (satisfactory) parameter estimates for both distributions are also confirmed.
Acknowledgements
Dr. ZORICA Cvetković from the Astronomical Observatory in Belgrade is the author of the FORTRAN programmes who performed the calculations in the examples. The ALHIDADA D.O.O. Company from Petrijevci (Croatia) has financially supported the publishing of the article. The figures were made by Darko Andjic, Dr. and graduated engineer of Geodesy from the Republic Geodetic Authority, Podgorica, Montenegro.
NOTES
1PEROBLS D is an abbreviation of the initial letters: Perović’s Robust Least-Square Method; D—by distribution Decomposing.