Mathematical Modeling Algorithms for Creating New Materials with Desired Properties Using Nano-Hierarchical Structures ()
1. Introduction
The idea of multiscaled phenomena in solids during their plastic deformation and destruction was formulated in the Tomsk school of solid state physics as the concept of structural levels of deformation of solids [3]. Structural levels of deformation belong to the class of mesoscopic scales. It is not always realized that the mesoscopic approach is a fundamentally new paradigm, qualitatively different from the methodology of continuum mechanics (macro scale approach) and dislocation theory (micro scale approach). Experimental and theoretical studies of mesoscopic structural levels of deformation led to a qualitatively new methodology for describing a deformable solid as a multi-level self-consistent system. Formed at various scale levels, disoriented substructures are a large-scale invariant. This is the basis for constructing a multilevel model of a deformable solid body, in which the entire hierarchy of scales of structural levels of deformation is taken into account. In the coming decades, the most relevant areas of work in the field of physical mesomechanics should be considered: the application of methods of physical mesomechanics of structurally heterogeneous media to the problems of modern materials science, including nanomaterials, thin films and multilayer structures, surface hardening and application of hardening and protective coatings. When constructing a mathematical model of a real object, it is necessary to use, as a priori information, active and passive monitoring data obtained during the current operation of the facility. At present, the following is very significant: the interaction between physics and mathematics is becoming more pronounced, the influence of the needs of physics on the development of mathematical methods, and the inverse effect of mathematics on physical knowledge. In a number of questions of physics and technology, a number of problems arose for which the apparatus of linear mathematics was either insufficient or even completely inapplicable [4]. For a comprehensive coverage of various phenomena in acoustics and mechanics, the mathematical apparatus of linear differential equations is absolutely insufficient. It is precisely those phenomena that are most characteristic and interesting here that obviously do not fit into its framework. The fact is that differential equations that adequately describe these phenomena are obviously nonlinear. Accordingly, we are talking about “nonlinear” systems. The foundations of the mathematical apparatus, adequate not only to individual problems, but to the entire cycle of nonlinear problems, are laid down in the famous works of Poincare, Lyapunov and Arnold [5] [6].
In papers [7] [8], modeling algorithms were constructed in the electromagnetic case for 3-D heterogeneities, in the seismic case for 2-D heterogeneities for an arbitrary type of excitation source of an N-layer medium with a hierarchical elastic inclusion located in the J-th layer. In work [9], a new 2D modeling algorithm for sound diffraction on elastic and porous, moisture-saturated inclusion of a hierarchical structure located in the J-th layer of an N-layer elastic medium was developed. In [10], modeling algorithms were constructed in the acoustic case for a 2-D heterogeneity for an arbitrary type of excitation source of an N-layer medium with a separate hierarchical anomalous density, stressed and plastic inclusions located in the J-th layer.
In this paper, using the method described in [6] [7] [8] [9], an algorithm for modeling the acoustic field (longitudinal acoustic wave) has been developed in the form of an iterative process for solving a direct problem for the case of three hierarchical inclusions of l, m, s-ranks using 2D integral and integro-differential equations. The degree of hierarchy of inclusions is determined by the values of their ranks, which can be different. Hierarchical inclusions are located in different layers above each other: the top is anomalously plastic (in layer j-1), the second is anomalously elastic (in layer j) and the third is anomalously dense (in layer j + 1).
2. Algorithm of Modeling Sound Diffraction on a Two-Dimensional Block N-Layered Medium with Composite Hierarchical Type Inclusions
In the paper [11] an algorithm for simulating the diffraction of sound on a two-dimensional elastic hierarchical inclusion located in the J-layer of an N-layer medium is described.
—function of the source of the seismic field, the boundary value problem for which was formulated in [12] [13]:
(1)
is the wave number in the elastic medium for the longitudinal wave, in the above expression the index ji denotes the property of the medium inside the heterogeneity, ja is outside the heterogeneity, λ is the Lamé constant, σ is the density of the medium, ω is the circular frequency,
,
is the displacement vector,
potential of seismic field in a layered medium in the absence of the heterogeneity:
.
—the potential of a normal seismic field in a layered medium in the absence of an heterogeneity of the previous rank l if
,
, if
,
which coincides with the corresponding expression [14]. We shall assume, following [15], that:
, (2)
where
and
for all ranks l, which is determined by the influence of internal friction in the inclusion according to the Focht model [15]. Then acoustic sounding of the second hierarchical inclusion will occur either at two independent frequencies, or at a certain frequency interval between
and
with the joint effect of the elastic parameters of the first inclusion:
and
. These properties will be reflected further in the excitation of the second and third hierarchical inclusions, and then in the transition from one hierarchical level to another. Let the rank values for all hierarchical inclusions:
, then the system of equations describing the propagation of a longitudinal acoustic wave in the first inclusion will be written as:
(3)
We calculate
in the layer where the second hierarchical elastic inclusion is located using expression (4), then the normal acoustic field potential for the second inclusion is written in the form:
. The system of equations for the second elastic hierarchical inclusion of rank m = 1 has the form according to [10] [11]:
(5)
(6)
Let’s calculate
, in the layer where the third hierarchical anomalous density inclusion is located using expression (6), then the normal potential of the acoustic field is:
.
(7)
We assume that the elastic parameters of the third hierarchical inclusion for all ranks s and the enclosing layer are identical, and the density of the hierarchical inclusion for all ranks differs from the density of the host environment, then the system of equations for the third hierarchical inclusion of rank s = 1 has the form according to [5] (7).
—the function of the source of the seismic field, it coincides with the function [12] [13],
—the wave number for the longitudinal wave and the elastic parameters for all s, in the above expression, the index ji denotes the property of the medium inside the heterogeneity, ja—outside the heterogeneity,
is the number of the hierarchical level,
is the potential of the normal acoustic field in the layer j + 1 in the absence of the third heterogeneity of the previous rank. We calculate
in layer j − 1 using expression (8):
(8)
The values of L, M, and S are the maximum values of the ranks of the hierarchy for the three inclusions. In this paper,
(8’)
;
;
. If
or
,
then we turn to the algorithm (3)-(8). If
, and , then we calculate
, then we calculate 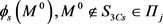 in layer j c using expression (9):
in layer j c using expression (9):
 (9)
(9)
 and we proceed to the algorithm (5)-(8), if
and we proceed to the algorithm (5)-(8), if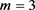 ,
,  then we turn to the algorithm (5)-(8). If
then we turn to the algorithm (5)-(8). If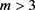 , and
, and 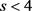 or
or ,
, 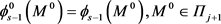 then we go to (7)-(8). If
then we go to (7)-(8). If 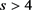 then we pass to (10).
then we pass to (10).
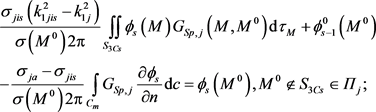 (10)
(10)
We calculate  in all the layers
in all the layers  using expression (10). The algorithm stops if the hierarchy ranks become larger than the given numbers (8’). If at some hierarchical level the structure of the local heterogeneity breaks up into several heterogeneities, then the double and contour integrals in expressions (3)-(10) are taken over all heterogeneities of a given rank.
using expression (10). The algorithm stops if the hierarchy ranks become larger than the given numbers (8’). If at some hierarchical level the structure of the local heterogeneity breaks up into several heterogeneities, then the double and contour integrals in expressions (3)-(10) are taken over all heterogeneities of a given rank.
3. Conclusion
Iterative modeling algorithms are constructed in the seismic case in the acoustic approximation for a composite hierarchical heterogeneity. For the first time, the proposed iterative algorithm for modeling a hierarchically complex hierarchical environment can be used for monitoring studies of the stability of complex hierarchical structures under various mechanical influences. That algorithm can be used for more complicated hierarchical media of many ranks with different physical-mechanical features. If the acoustic features of the material differ from the needed we increase the parameters L, M, S and continue calculation of the acoustic field for other ranks with more complicated structures of the hierarchical inclusions with smaller dimensions up to nano dimensions.