Algorithm for the Vertex Connectivity Problem on Circular Trapezoid Graphs

Hirotoshi Honma, Kento Nishimura, Yuto Tamori, Yoko Nakajima

National Institute of Technology, Kushiro College, Kushiro, Japan.

DOI: 10.4236/jamp.2019.711177                

Abstract

The vertex connectivity k(G) of a graph G is the minimum number of nodes whose deletion disconnects it. Graph connectivity is one of the most fundamental problems in graph theory. In this paper, we designed an O(n²) time algorithm to solve connectivity problem on circular trapezoid graphs.

Keywords

Algorithm Design, Connectivity Problem, Intersection Graphs, Circular Trapezoid Graphs

1. Introduction

The vertex connectivity $\kappa \left(G\right)$ of a graph G is the minimum number of nodes whose deletion disconnects it. The computation of $\kappa \left(G\right)$ for a given graph G is known as the vertex connectivity (vertex connectivity) problem, and it is one of the most fundamental problems in graph theory. In recent years, many studies related to vertex connectivity have been conducted [1] - [6]. Even and Tarjan developed an $O\left(m{n}^{1.5}\right)$ time algorithm to calculate the vertex connectivity of a general graph [7]. In many cases, more efficient algorithms can be developed by restricting the classes of graphs. For example, Ghosh and M. Pal presented an $O\left(n^2\right)$ time algorithm to solve the VC problem for trapezoid graphs [8]. Subsequently, this algorithm was improved by Ilić [9] to $O\left(n\log n\right)$ time by using a binary indexed tree.

Lin introduced circular trapezoid graphs (CTG), which constitute a proper superclass of trapezoid graphs and circular-arc graphs [10]. He also presented $O\left(n^2\log \log n\right)$ time and $O\left(n^2\log n\right)$ time algorithms for the maximum weighted independent set and the minimum weighted independent dominating set on CTGs, respectively [10]. In this paper, we designed an $O\left(n^2\right)$ time algorithm to solve the VC problem on CTGs. Our algorithm was realized by skillfully combining the methods of [9] and [11].

The rest of this paper is organized as follows. Section 2 describes some definitions of circle trapezoid graphs and models and introduces the extended circle trapezoid model, as well as some notations. Section 3 presents some properties on circle trapezoid graphs, which are useful for finding vertex connectivity in an efficient manner. Section 4 describes our algorithm for the VC problem and its complexity. Finally, Section 5 concludes the paper.

2. Definitions

We describe the circular trapezoid model (CTM) before defining the CTG. The model comprises inner and outer circles C₁ and C₂ with radii $r_1<r_2$, respectively. Each circle is arranged counterclockwise with consecutive integer values $\mathrm{1,2,}\cdots \mathrm{,2}n$, where n is the number of trapezoids. Consider the two arcs, A₁ and A₂, on C₁ and C₂, respectively. Points a and b are the first points encountered when traversing the arc A₁ counterclockwise and clockwise, respectively; similarly, points c and d are the first points encountered when traversing the arc A₂ counterclockwise and clockwise, respectively. A trapezoid is the region in circles C₁ and C₂ that lies between two non-crossing chords ac and bd. A trapezoid $C{T}_i$

is defined by four corner points $\left[a_i\mathrm{,}{b}_i\mathrm{,}{c}_i\mathrm{,}{d}_i\right]$. Without loss of generality, we assume that each trapezoid has four distinct corner points. Each trapezoid $C{T}_i$ is numbered in ascending order according to their corner point $a_i$, i.e., $i<j$ if $a_i<a_j$. The geometric representation described above is the CTM. Figure 1 (a)

illustrates an example of a CTM M having 8 trapezoids. For example, CTM is used for cities comprising cityscapes that spread radially around facilities such as stations and rotaries. It is used to visually represent the relationships among communities (linkage of transportation networks, sharing of infrastructure facilities, etc.), and it is applied to the optimization of city planning and facility arrangement. Table 1 shows the details of M as depicted in Figure 1(a).

(a) (b)

Figure 1. Circular trapezoid model M and graph G. (a) Circular trapezoid model M; (b) Circular trapezoid graph G.

Table 1. Details of CTM M.

A graph G is a CTG if it can be represented by the following CTM M: each vertex of the graph corresponds to a trapezoid, and two vertices in G are considered adjacent if and only if their corresponding trapezoids intersect. Figure 1(b) illustrates the CTG G corresponding to CTM M shown in Figure 1(a). In this example, G is disconnected by removing vertices 1, 5, and 6 from G. Thus, the vertex connectivity of G is 3.

In the following, we introduce an extended circular trapezoid model (ECTM) constructed from a CTM. Let n be the number of trapezoids in CTM M. Consider a fictitious line p that connects the points placed between 1 and 2n of C₁ and C₂. First, we cut CTM along fictitious line p and expand the two circles C₁ and C₂ into parallel horizontal lines called top and bottom channels, respectively.

Hereafter, to avoid confusion, we denote trapezoids in CTM and ECTM by $C{T}_i$ and $T_i$, respectively. Finally, for each $T_i$, $1\le i\le n$, copies of $T_{i+n}$ and $T_{i-n}$ are created by shifting 2n to the right and left, respectively. An ECTM is constructed from a CTM by the above process, which can be executed in $O\left(n\right)$ time [11]. Figure 2 illustrates an ECTM EM constructed from the CTM M shown in Figure 1(a). Table 2 shows the details of EM.

Some notations that form the basis of our algorithm in Section 4 are defined as follows. A separating set in a connected graph G is a set of vertices whose deletion disconnects G. We introduce a new concept to ECTM that is similar to the separating set in CTG. A separating trapezoid set in an ECTM EM is a set of trapezoids whose deletion separates EM into two or more components. Let S be a separating trapezoid set of EM. $EM-S$ is a trapezoid set that is obtained by deleting S from all trapezoid sets of EM. If $EM-S$ has k components, we denote $n_c\left(EM-S\right)=k$. Moreover, let $G\left[EM-S\right]$ be a induced subgraph of G by the trapezoid set $EM-S$.

3. Properties of Vertex Connectivity on TCGs

We describe some lemmas that are useful for constructing the algorithm for the VC problem.

Lemma 1. [11] For a given CTM M, an ECTM EM corresponding to M is constructed in $O\left(n\right)$ time.

Lemma 2. [9] For a trapezoid graph G, the VC problem is solved in $O\left(n\log n\right)$ time.

Lemma 3. [9] By Lemma 2, for an ECTM EM, all smallest separating trapezoid sets can be found in $O\left(n\log n\right)$ time.

Table 2. Details of ECTM EM.

Figure 2. Extended circular trapezoid model EM.

Lemma 4. [11] Let S be a separating trapezoid set of an ECTM EM. Then, for an ECTM EM, we can compute $n_c\left(EM-S\right)$ in $O\left(n\right)$ time.

Lemma 5. Let G be a CTG G corresponding to an ECTM EM and let S be a separating trapezoid set of EM. Then, a CTG $G\left[EM-S\right]$ is connected if $n_c\left(EM-S\right)=2$. Furthermore, a CTG $G\left[EM-S\right]$ is disconnected if $n_c\left(EM-S\right)\ge 3$.

(Proof) If EM consists of one component, it is obvious that G is connected. We consider the case when $n_c\left(EM-S\right)=2$, i.e., EM consists of two components. Assume that EM is divided into two components C_i and C_j, and vertices $v_i$ and $v_j$ ( $i<j$ ) are in C_i and C_j, respectively. A trapezoid that intersects a fictitious line p is called a feedback trapezoid, where p connects the points placed between 1 and 2n of C₁ and C₂ in CTM M. No path exists from $v_i$ to $v_j$ through $v_k$ for $v_i\mathrm{,}{v}_k\mathrm{,}{v}_j$ ( $i<k<j$ ) since EM is divided into two components C_i and C_j. However, some paths exist from $v_i$ to $v_j$ through some feedback trapezoids. Thus, in the case where EM consists of two components, G is connected. In the case where EM consists of three or more components, no path exists from $v_i$ to $v_j$ through or even through feedback trapezoids. This implies that CTG G corresponding to CTM M is disconnected.

4. Algorithm

4.1. Outline of Algorithm

Efficient algorithms that address various problems concerning non-circular intersection graphs (interval, permutation, trapezoid, etc.) have been developed. However, in general, problems for circular intersection graphs tend to be more difficult than those for non-circular intersection graphs. One cause is because, in contrast to non-circular intersection graphs, we cannot determine the starting position of an algorithm uniquely for a circular intersection graph owing to the existence of feedback elements. For several problems, we can develop circular versions of the existing algorithms by constructing extended intersection models for the problems. By using extended intersection models such as an ECTM, we can determine the start position of an algorithm uniquely and apply the algorithms of the non-circular versions partially. For instance, this method has been applied to develop efficient algorithms for the shortest path query problem [12] [13] and the articulation vertex problem [14] on circular-arc graphs, maximum clique and chromatic number problems [15], the spanning forest problem [16] and the articulation problem [17] on circular permutation graphs, and the spanning tree problem [11] and the hinge vertex problem [18] on circular trapezoid graphs.

Here, we concisely describe the outline of our algorithm. When a given CTG has articulation vertices, the vertex connectivity is 1. We can find articulation vertices in $O\left(n+m\right)$ time by applying the traditional method with depth first search. Then, we discuss graphs that do not contain articulation vertices.

First, we construct an ECTM EM from a given CTM M by using Honma et al.’s algorithm [11] (Figure 2). Next, we compute the family of minimum cardinality separating trapezoid set $F_S=\left\{S_1,S_2,\cdots ,S_m\right\}$ for a constructed EM. In the example in Figure 2, we obtain $F_S=\left\{\left\{T_1\right\}\right\}$ and $n_c\left(EM-\left\{T_1\right\}\right)=2$. At this time, if even one S_i exists such that $n_c\left(EM-S_i\right)\ge \mathrm{3,}{S}_i\in F_S$, the size of S_i is the vertex connectivity of CTG G, by Lemma 5. By Lemma 4, for each $S_i\in F_S$, $n_c\left(EM-S_i\right)$ can be computed in $O\left(n\right)$ time by Honma et al.’s algorithm [11].

Conversely, we consider the case where multiple $S_i\mathrm{,1}\le i\le m$ exist such that $n_c\left(EM-S_i\right)=2$. In this case, $G\left[EM-S_i\right]$ is a connected graph for every S_i, by Lemma 5. In this case, a CTM $M-S_i$ has a fictitious line connecting C₁ and C₂ that does not intersect any trapezoid in $M-S_i$ (Figure 3(a)). The model opened along this line is equivalent to a regular trapezoid model, and we denote it as $E{M}^{\prime }$ (Figure 4). Again, we compute the minimum cardinality separating trapezoid sets ${S^{\prime }}_i$ of $E{M}^{\prime }$ by using Ilić’s algorithm [9]. In the example of Figure 4, we obtain ${S^{\prime }}_i=\left\{T_5,T_6\right\}$.

After this process, $n_c\left(EM-S_i-{S^{\prime }}_i\right)\ge 3$ holds and $G\left[EM-S_i-{S^{\prime }}_i\right]$ is disconnected, by Lemma 5. We can obtain the vertex connectivity of G by ${\min }_{i=1}^m\left|S_i\cup {S^{\prime }}_i\right|$. We formally describe Algorithm VC-CTG as follows. A CTM M is taken as an input. Our algorithm uses both Ilić’s and Honma et al.’s algorithms [9] [11].

4.2. Algorithm VC-CTG and Its Analysis

In this section, we present Algorithm VC-CTG to compute the vertex connectivity of a CTG G. We formally describe Algorithm VC-CTG as follows. A CTM M is taken as an input. Our algorithm uses both Ilić’s and Honma et al.’s algorithms [9] [11].

(a) (b)

Figure 3. Circular trapezoid model $M-\left\{T_1\right\}$ and graph $G\left[M-\left\{T_1\right\}\right]$. (a) CTM $M-\left\{T_1\right\}$ ; (b) CTG $G\left[M-\left\{T_1\right\}\right]$.

Figure 4. Extended circular trapezoid model $E{M}^{\prime }$.

Here, we analyze the complexity of Algorithm VC-CTG. In Step 1, we check whether given graph G has articulation vertices using the traditional algorithm. Moreover, we return that vertex connectivity is 2 when the minimum degree of vertices in G is 2. This step can be done in $O\left(n+m\right)$ time. In Step 2, we construct an ECTM EM from a given CTM M as an input. This step can be performed in $O\left(n\right)$ time by using Honma et al.’s algorithm [11]. In Step 3, we first compute all minimum cardinality separating trapezoid sets $F_S$. This process can execute in $O\left(n\log n\right)$ time by using Ilić’s algorithm [9]. Here, we obtain the vertex connectivity $\left|S_i\right|$ of G if there exists $S_i\in F_S$ such that $n_c\left(EM-S_i\right)\ge 3$. This can execute in $O\left(n\log n\right)$ time by using Honma et al.’s algorithm [11]. In Step 4, we compute a minimum cardinality separating trapezoid set ${S^{\prime }}_i$ of $EM-S_i$ for each $S_i\in F_s$. Step 3 requires time. Thus, we obtain the following theorem.

Theorem 6. Algorithm VC-CTG computes the vertex connectivity of CTG in 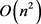time by taking its CTM M as an input.

5. Conclusion

In this study, we proposed Algorithm VC-CTG, which operates in time, to compute the vertex connectivity of a CTG. Our algorithm uses both Ilić’s and Honma et al.’s algorithms [9] [11]. CTM is used for cities comprising cityscapes that spread radially around facilities such as stations and rotaries. It is used to visually represent the relationships among communities (linkage of transportation networks, sharing of infrastructure facilities, etc.), and it is applied to the optimization of city planning and facility arrangement. Solutions to the VC problem can be applied to detect connection vulnerabilities in actual networks. Thus, we believe that this paper is significant from both theoretical and algorithmic perspectives. Future research will address reducing the complexity of the algorithm and extending the results to other graphs.

Acknowledgements

We express many thanks to anonymous referees for their valuable advices on the theory of our attacks and their helpful editorial comments. This work was partially supported by JSPS KAKENHI Grant Number 19K11834 and 17K00324.

Conflicts of Interest

The authors declare no conflicts of interest regarding the publication of this paper.

References

[1]	Goddarda, W., Rainesb, M.E. and Slaterc, P.J. (2003) Distance and Connectivity Measures in Permutation Graphs. Discrete Mathematics, 271, 61-70. https://doi.org/10.1016/S0012-365X(02)00870-1
[2]	Shang, Y. (2009) Connectivity in a Random Interval Graph with Access Points. Information Processing Letters, 109, 446-449. https://doi.org/10.1016/j.ipl.2009.01.002
[3]	He, J. and Liang, H. (2012) On Rainbow-k-Connectivity of Random Graphs. Information Processing Letters, 112, 406-410. https://doi.org/10.1016/j.ipl.2012.01.014
[4]	Chen, L., Peng, J., Rao, C. and Rosyida, I. (2018) Cycle Index of Uncertain Random Graph. Journal of Intelligent & Fuzzy Systems, 34, 4249-4259. https://doi.org/10.3233/JIFS-17373
[5]	Schmidt, J.M. (2013) A Simple Test on 2-Vertex- and 2-Edge-Connectivity. Information Processing Letters, 113, 241-244. https://doi.org/10.1016/j.ipl.2013.01.016
[6]	Chen, L., Peng, J. and Ralescu, D. (2019) Uncertain Vertex Coloring Problem. Soft Computing, 23, 1337-1346. https://doi.org/10.1007/s00500-017-2861-7
[7]	Even, S. and Tarjan, R.E. (1975) Network Flow and Testing Graph Connectivity. SIAM Journal on Computing, 4, 507-518. https://doi.org/10.1137/0204043
[8]	Ghosh, P.K. and Pal, M. (2007) An Efficient Algorithm to Solve Connectivity Problem on Trapezoid Graphs. Journal of Applied Mathematics and Computing, 24, 141-154. https://doi.org/10.1007/BF02832306
[9]	Ilić, A. (2013) Efficient Algorithm for the Vertex Connectivity of Trapezoid Graphs. Information Processing Letters, 113, 398-404. https://doi.org/10.1016/j.ipl.2013.02.012
[10]	Lin, W.L. (2006) Circular and Circle Trapezoid Graphs. International Journal of Scientific Engineering and Technology, 2, 11-17.
[11]	Honma, H., Nakajima, Y., Aoshima, Y. and Masuyama, S. (2013) A Linear-Time Algorithm for Constructing a Spanning Tree on Circular Trapezoid Graphs. IEICE Transactions on Fundamentals, E96-A, 1051-1058.
[12]	Chen, D., Lee, D.T., Sridhar, R. and Sekharam, C. (1998) Solving the All-Pair Shortest Path Query on Interval and Circular-Arc Graphs. Networks, 31, 249-258. https://doi.org/10.1002/(SICI)1097-0037(199807)31:4<249::AID-NET5>3.0.CO;2-D
[13]	Hsu, F.R., Shan, K., Chao, H.S. and Lee, R.C. (2005) Some Optimal Parallel Algorithms on Interval and Circular-Arc Graphs. Journal of Information Science and Engineering, 21, 627-642.
[14]	Kao, T.W. and Horng, S.J. (1995) Optimal Algorithms for Computing Articulation Points and Some Related Problems on a Circular-Arc Graph. Parallel Computing, 21, 953-969. https://doi.org/10.1016/0167-8191(95)00007-B
[15]	Lou, R.D. and Sarrafzadeh, M. (1992) Circular Permutation Graph Family with Applications. Discrete Applied Mathematics, 40, 433-457. https://doi.org/10.1016/0166-218X(92)90012-Y
[16]	Honma, H., Honma, S. and Masuyama, S. (2009) An Optimal Parallel Algorithm for Constructing a Spanning Tree on Circular Permutation Graphs. IEICE Transactions on Information and Systems, E92-D, 141-148.
[17]	Honma, H., Abe, K., Nakajima, Y. and Masuyama, S. (2013) Linear Time Algorithms for Finding Articulation and Hinge Vertices of Circular Permutation Graphs. IEICE Transactions on Information and Systems, E96-D, 419-425.
[18]	Honma, H., Nakajima, Y. and Masuyama, S. (2017) An Algorithm for Hinge Vertex Problem on Circular Trapezoid Graphs. Journal of Information Processing, 25, 945-948.