Energy Consumption, Economic Growth and Carbon Emissions: Evidence from the Top Three Emitters in Africa ()
1. Introduction
According to Intergovernmental Panel on Climate Change [1] [2] , climate change will have adverse impacts on the ecosystem, food security, water and human health. The negative impacts on climate change will be particularly severe in developing countries, due to their limited capacity to cope with the problem generated by climate change. For instance, Nordhaus and Boyer [3] estimate that the rise of average temperatures to 2˚C would reduce the per capita annual consumption by 4% to 5% in Africa and Asia respectively. Hope [4] estimates that developing countries would bear 75% to 80% of the total costs of climate change.
Since the seminal works of Grossman and Krueger [5] , Shafik and Bandyopadhyay [6] and Panayotou [7] on the environmental effects of economic growth that led to the existence of an Environmental Kuznets Curve (EKC)1 [8] which postulates an inverted U-shaped relationship between economic growth and environmental degradation [7] , there is an increasing emphasis on the determinants of environmental degradation.
In addition to economic growth, energy generation and consumption are listed as key determinants of environmental degradation. The International Energy Agency [11] estimates that the energy sector accounts for 68% of the total greenhouse gases (GHG) emitted around the world. Specifically, from the late 1980s to the early 2000s, coal and oil were each responsible for approximately 40% of global CO2 emissions. Moreover, the IPCC [1] predicts that energy-related CO2 emissions in 2030 would have increased by 40% - 110%. This is linked to the fact that the world-wide energy consumption will, on average, continue to increase to 56% by 2040 [12] .
At the empirical level, authors have introduced energy consumption in the EKC model as an additional determinant of environmental quality based on the study of Ang [13] who finds a positive and significant effect of energy consumption on carbon emissions in France. The literature on the topic can be summarized into two main strands. The first strand uses aggregate measures of energy consumption. For example, Boutabba [14] , Heidari et al. [15] , Saboori et al. [16] find that energy consumption has a positive and significant effect on CO2 emissions. Authors of the second strand use disaggregated measures of primary energy consumption. Halicioglu [17] finds that commercial energy consumption has a positive effect on carbon emissions in Turkey between 1965 and 2005 period. Shafiei and Salim [18] show that an increase in non-renewable energy consumption increases CO2 emissions, while renewable energy reduces them in a panel of OECD countries from 1981 to 2011.
1It is derived from the Income-inequality relation developed by Simon Kuznets in1955 [8] . According to Kuznets, there is an inverted relationship between economic growth and inequality. Dinda [9] ; and Kaika and Zervas [10] proposed a comprehensive literature survey on the EKC hypothesis.
In African economies, there is a growing debate on the effects of economic growth and energy consumption on carbon emissions. Some studies devoted to these countries include Akpan and Akpan [19] in Nigeria, Shahbaz et al. [20] in South Africa, Jebli et al. [21] on a panel of 24 Sub-Saharan African countries, Nkengfack and Kaffo [22] in Cameroon, Gabon, Congo and Democratic Republic of Congo, Bouznit and Pablo-Romero [23] in Algeria. Several reasons justify the choice of these countries. Firstly, they accounted for 66.34% of CO2 emitted by African countries in 2015 [11] . This represents 130.4 million tons for Algeria, 198.6 million tons for Egypt and 427.6 million tons of CO2 for South Africa on the over 1140.4 million tons of carbon emitted by African countries in 2015 (see Appendix 1 for carbon profile in Africa in 2015). Secondly, data suggests that these countries recorded positive average growth rates of GDP of approximately 3% since 2000 (calculated using World Development Indicators, 2017). Thirdly, they highly depend on conventional energy sources which are highly polluting. For instance, the South African energy sector is dominated by coal and crude oil production with respectively 69.39% and 23.20% of primary energy production in 2015. Algerian and Egyptian primary energy supply is mainly covered by natural gas and crude oil, with respective proportions of 64.33% and 35.31% for Algeria, and 49.65% and 47.72% for Egypt in 2015 (computed from the BP World Statistic Review on energy, 2017).
In addition, we investigate the inter-relationship between economic growth, energy consumption and CO2 emissions. To do this, we use the Toda-Yamamoto [24] Granger non-causality approach to check the causal relationship between our variables. The main reason for this method is that it is valid regardless of whether a series is I(0), I(1) or I(2), cointegrated or not-cointegrated [25] .
To the best of our knowledge, the only serious empirical study that focuses particularly on the link between carbon emissions, energy consumption and economic growth is that of Ahmad et al. [26] . These authors analyze the long and short run relationship between carbon emissions, energy consumption and economic growth in India at the aggregated and disaggregated levels over the period 1971-2014. The long-run results show that energy (primary energy, gas, oil, electricity and coal) consumption has a positive impact on carbon emissions. Other studies were more interested, at the methodological level, in checking the cointegration and causal relationships between economic growth, energy consumption and carbon emissions [14] [17] [27] [28] [29] [30] [31] . These studies however produce mixed results on the relationship between economic growth, energy consumption and carbon emissions. The present paper is therefore related to Ahmad et al. [26] . It is added to the existing literature on the relationship between economic growth, energy consumption and carbon emissions in Africa by investigating the effects of energy consumption and economic growth on carbon emissions in the top three emitters in Africa (Algeria, Egypt and South Africa), using aggregated and disaggregated measures of energy consumption. The disaggregation helps to eliminate the potential aggregation bias and shows a picture of the effect of different sources of energy on carbon emission. In addition, we implement the Toda-Yamamoto Granger non causality test in order to capture the types of relationship between economic growth, energy consumption and energy consumption.
After the introduction, the remainder of this paper is structured as follows. Section two presents the data, the modeling approach and the estimation technique. Section three presents and discusses the main results. Section 4 deals with conclusion and policy implications.
2. Data, Modeling and Estimation Technique
2.1. Data, Descriptive Statistics and Correlations
To assess the effect of economic growth and carbon emissions in Algeria, Egypt and South Africa, we use annual time series data covering the 1971-2015 period, period during which data were available. Data on aggregated energy consumption (primary energy consumption) and disaggregated energy consumption (coal, electricity, oil and natural gas) are taken from the BP Statistical Review of World Energy [32] . The data on per capita CO2emissions is extracted from the 2017 version of the International Energy Agency database while data on per capita GDP, trade openness, urbanization and share of industrial value (added as a percentage of GDP) are obtained from World Development Indicators issued by the World Bank [33] . The descriptive statistics and the correlation coefficients between the variables are presented in Appendix 2.
2.2. Modeling Approach
In order to empirically evaluate the effects of energy consumption and economic growth on CO2 emissions, we adopt the STIRPAT2 (Stochastic Impact by Regression on Population, Affluence and Technology) developed by Dietz and Rosa [35] . The standard STIRPAT model is expressed as follows:
(1)
In Equation (1), the environmental impact (I) is a function of the size of the population (P), Affluence (A) and Technology (T). a is a constant term, while b, c and d are the parameters associated to P, A and T respectively. e is the error term. The subscript t (t = 1971 … 2015) stands for time period.
Considering the variables of the previous equation in logarithms, we have:
(2)
In the log form, b, c and d are interpreted as elasticity of carbon with respect to population, Affluence and Technology, respectively.
However, the standard equation can be reformulated in other to account for the impact of additional variables on environmental degradation [36] . Hence, we formulate the following modified STIRPAT model, adding urbanization and trade as additional variables. These variables have been widely used as determinants of environmental degradation [16] [17] . The estimated equation is specified as follows:
(3)
where, CO2t is the per capita carbon emissions at time t, gdpc is the per capita real income (in constant 2010 US$), pener is primary energy consumption used as the aggregated measure of energy consumption, urb stands for the percentage of urban population in the total population and is used as proxy of urbanization, Trad is the openness ratio, used as a proxy for foreign trade. εt is the error term.
2The STIRPAT model is derived from the IPAT model formulated by Ehrlich and Holdren [34] .
From Equation (3), primary energy consumption is segmented into four subcomponents: coal, oil, electricity and natural gas to account for any potential aggregation bias.
In Equation (4), coal consumption is used as energy consumption:
(4)
In Equation (5), oil consumption is used as energy consumption:
(5)
In Equation (6), electric power consumption is used as energy consumption:
(6)
In Equation (7), natural gas consumption is used as energy consumption:
(7)
2.3. Estimation Technique
1) Unit root test
As a starting point of the analysis, we test the stationary of our variables in order to avoid the problems of spurious regressions and time-variant estimates. Traditionally, the Augmented Dickey-Fuller and the Phillips-Perron tests are used to test for the present of unit root when time series data are considered. However, the principal limitation is that they do not account for structural breaks in time series [37] . In fact, it is recognized that the presence of structural breaks in the time series may bias the results toward non rejection of the null hypothesis of unit root when there is none. To overcome such an issue, we use unit root tests of Zivot and Andrews [38] which allows an endogenous break in time series data. The null hypothesis admits that the series have a unit root while the alternative hypothesis assumes that they are stationary with one break.
2) Cointegration analysis
This paper applies the ARDL bound testing approach to cointegration developed by Pesaran and Shin [39] and Pesaran et al. [40] . Contrary to traditional unit root tests (Engle and Granger, Johansen test, Johansen and Juselius test), the bound testing approach is applicable if variables are integrated of different orders: I(0), I(1) or fractionally integrated. In addition, the bound testing approach is relatively more efficient in the case of small and finite data samples. Lastly, by applying the bound testing approach, we obtain unbiased estimates of the long run model [41] .
The cointegration test is carried out on the following Unrestricted Error correction Models (UECM) for primary energy consumption, coal consumption, oil consumption, electric power consumption and natural gas consumption:
(8)
In Equation (8), the terms at level capture the long run dynamics while the terms with the sum (∑) and difference (Δ) operators capture the short run dynamics. p and q indicate the optimal lag lengths, determined by the Akaike Information Criteria (AIC) and Schwarz Information Criteria (SIC). Other variables remain unchanged.
The null hypothesis of absence of cointegration (
) is tested against the alternative hypothesis of cointegration (
). The F-statistics resulting from the estimation of equation (8) is compared to the theoretical bounds tabulated by Pesaran et al. [40] . The lower critical bound (LCB) assumes that all the variables of the model are I(0) while the upper critical bound (UCB) assumes that all the variables of the model are I(1). If the computed F-statistic exceeds the UCB, the null hypothesis of no cointegration is rejected. If the F-statistic is lower than the LCB, the alternative hypothesis of cointegration is rejected. Finally, if the F-stat lies between LCB and UCB, the result is inconclusive. In this case, the error correction term is a useful way of establishing cointegration.
Once long run relationship has been established, the Error correction Models (ECM) is estimated by using the ordinary least squares method and the AIC and SIC to select the lag order of the ARDL model. In this study, ECM associated to Equation (8) is formulated as follows:
(9)
where η measures the speed of adjustment to obtain equilibrium in the event of shock(s) to the system and ECTt-1 is the error correction term obtained from the estimation of the long run equations. Other variables remain unchanged.
In order to ensure the suitability of the model, diagnostic and stability test will be conducted. Diagnostic tests include tests for normality, serial correlation and heteroskedasticity for the different models. Then the cumulative sum (CUSUM) and cumulative sum of squares (CUSUMSQ) tests have been applied in order to ensure the stability of the models.
3) Toda Yamamoto test of non-causality
Next to the ARDL, we test the causal relationship between energy consumption, economic growth and carbon emission through the Toda and Yamamoto [21] which is modified version of the Granger causality test. Implementing the Toda and Yamamoto test involves estimating the following Vector Auto Regressive (VAR) model, where the optimal lags p are determined by the AIC or SIC:
(10)
where d is the maximum order of integration of our variable, εit (i = 1, …, 5) are the error terms, other variables remain unchanged.
3. Results and Discussions
3.1. Unit Root Tests
According to the results of Zivot and Andrews [38] unit root test provided in Table 1, the maximum order of integration of our variables is I(1) for Algeria, Egypt and South Africa. In addition, our variables present structural break dates.
3.2. Cointegration Test Results
Table 2 reports the results of the bound test for cointegration when primary energy, coal consumption, oil consumption, electric power consumption and natural gas consumption are used as proxies of energy consumption. The result for the electric power consumption model for Egypt, oil and natural gas models for South Africa are inconclusive, indicating that it is not possible to choose between the null hypothesis of nocointegration and the alternative hypothesis of cointegration. In fact, the calculated F-statistic for those models lies between the LCB and the UBC. For these models, the decision about the presence or absence of cointegration depends on the sign and significance of the error correction term.
The bound test is conclusive for the remaining models, implying the presence of both short and long-run relationship between our variables. In fact, the calculated F-statistic is greater than the UCB.
![]()
Table 1. Zivot and Andrews [38] unit test.
Note: Values in brackets are structural break dates for each variable. ***, ** and * indicate significance at 1%, 5% and 10% levels respectively.
![]()
Table 2. Bound test of cointegration.
Note: *** and * indicate significance at 1% and 10% levels respectively. incindicates that the cointegration test result is inconclusive. In this case, the decision will depend on the sign and significance of the error correction term associated to the respective equations.
3.3. Empirical Result Based on Aggregated Measures of Energy Consumption
Table 3 provides the results when primary energy consumption is used. Based on the AIC and the SIC, the optimal models are ARDL (2,0,0,0,0), ARDL (1,0,1,1,0) and ARDL (2,0,1,0,0), respectively for Algeria, Egypt and South Africa. In addition, our results provided in Table 3 passed the tests for non-normality, serial correlation, and heteroskedasticity. To ensure the short-run and long run stability of our models, the CUSUM and CUSUMSQ tests were carried out. Results show that the short run parameters are stable for Algeria and Egypt, while only the short run parameter are unstable in South Africa (CUSUM).The estimated coefficients of the error correction terms (ECTt-1) are significant with the appropriate signs at the 1% level, supporting the evidence of a long run relationship among variables.
Economic growth has a positive and significant impact on carbon emissions both in the long and short run. In the long-run, a 1% increase in per capita GDP will increase per capita carbon emissions by 0.451, 0.290 and 0.513 in Algeria, Egypt and South Africa, respectively. This finding is in line with Lin et al. [42] , Liu et al. [30] , and Chen and Lei [43] whose studies do not include a quadratic term of per capita GDP in their environmental impact model. However, the elasticity of carbon emissions with respect to income is lower than the value obtained by the above-mentioned authors. This result could be explained by the structure or composition of production in these countries. In fact, structural transformation in these countries is accompanied by a shift from the industrial to the service sector, which is generally considered as less pollutant intensive, than the industrial sector [7] .
Results in Table 4 also show that the elasticity with respect to primary energy is positive and statistically significant in the long-run and short-run. For instance, a 1% increase in primary energy consumption will lead to a 0.558, 0.901
![]()
Table 3. Primary energy consumption, economic growth and carbon emissions.
Note: ***, ** and * indicate significance at 1%, 5% and 10% levels respectively; J-B is the Jarque-Bera test for normality; B-G is the Breusch-Godfrey serial correlation LM Test; B-P is the Breusch-Pagan-Godfrey heteroskedasticity Test, Prob are the associated p-values.
and 0.228% increase in carbon emissions in Algeria, Egypt and South Africa in the short run. The corresponding effects in the long run are 0.528, 0549 and 0.101%. The results are in line with those of most studies in the literature such as Shahbaz et al. [20] , Farhani et al. [27] , Heidari et al. [15] , Inglesi-Lotz and Dogan [44] who find that energy consumption increases environmental degradation. Our result is attributed to the fact that the Algerian, Egyptian and South African economies are primarily based on the exploitation and the exports of fossil energies. Furthermore, fossil energy is still the main energy source in these economies.
Concerning the control variables, the elasticity of CO2 emissions with respect
![]()
Table 4. Estimation for disaggregated proxies of energy.
Note: (.) are standard errors; ***, ** and * indicate significance at 1%, 5% and 10%, respectively, J-B is the Jarque-Bera test for normality; B-G is the Breusch-Godfrey serial correlation LM Test; B-P is the Breusch-Pagan-Godfrey heteroskedasticity Test, Prob are the associated p-values.
to rate of urbanization is positive in the selected countries, although a significant impact is recorded only in Egypt. This result is consistent with Hooi and Smyth [29] , Halicioglu [17] , Akpan and Akpan [19] who find that urbanization has a positive impact on carbon emissions. However, it is important to note that the debate on the effect of economic growth on environmental degradation is still growing, since He et al. [45] find that above a certain development level, urbanization is not necessarily associated to the increase in CO2 emissions.
Trade openness has a negative and significant impact on CO2 emissions in Algeria in the long and short run, while the opposite effect is observed in South Africa in the long run. The effect of trade openness in Egypt is not significant both in the long and short run. This clearly indicates that the determinants of environmental degradation may differ across countries of the same region.
3.4. Empirical Results Based on Disaggregated Measures of Energy Consumption
The long and short run outcomes are reported in Table 4. The negative and significant coefficients associated to the error correction term (ECTt−1) confirm the cointegration hypothesis among the variables for the sub equations. Diagnostic tests indicate that the residual in the estimated equations are homoscedastic and non autocorrelated. The equations also pass the normality test. Cumulative sum (CUSUM) and cumulative sum of squared (CUSUMSQ) recursive residual tests indicate that some models are stable while others are not.
As it is the case for aggregate energy, economic growth has a positive and significant impact on carbon emissions in the short and long-run. In addition, urbanization has a positive and significant impact on CO2 emissions in Algeria and Egypt, and a non-significant impact in South Africa. Trade openness plays an ambiguous role in explaining carbon emissions in these countries. In Algeria, increase in the trade openness ratio has a negative effect on carbon emissions in the short-run and the long run. The effect of trade openness is positive and statistical significant only in the long term in South Africa, while the effect of this variable is positive but non-significant in Egypt. These results suggest that increase in the openness of Algeria is coupled with increase in the imports of less pollution-intensive goods and services. However, our result confirms the absence of consensus on the effects of trade openness on the environment; since the net effect is positive or negative depending on the level of development of countries [17] , the factor endowment according to which as openness proceeds, developing countries would change to net exporters of pollution-intensive goods and deteriorate their environmental quality [16] .
The most important result concerns the effects of disaggregated energy consumption (coal, oil, electricity and natural gas) on carbon emissions. The elasticity of per capita carbon emissions with respect to coal, oil, electricity and natural gas are positive and significant both in the long and short run in the selected countries. However, the magnitude of the coefficient differs between the proxies of energy consumption. In fact, oil consumption is the main energy source of CO2 emissions in Algeria, while power electric consumption and coal consumption are the major sources of CO2 emissions in Egypt and South Africa respectively. All thing being equal, 1% increase in oil, natural gas, electricity and coal consumption in Algeria leads to an increase in CO2 emissions by 0.953, 0.328, 0.201 and 0.093, respectively. In Egypt, a unit increase in per capita electric power consumption and oil consumption generates 0.409 and 0.253 units in per capita carbon emission, while the effects of coal and natural gas are insignificant. In South Africa, the respective elasticities are 0.889, 0.553, 0.134 and 0.039 for coal, oil, electricity and natural gas consumption.
3.5. Toda Yamamoto Non-Causality Results
The results of Toda Yamamoto test for no-causality are reported in Table 5. As we are relatively more interested in the interrelationships between economic growth, energy consumption and carbon emissions, we concentrate on results relating to those variables.
The results on the direction of the causality are summarized in Table 6, where the source and the direction of causality between the variables are also reported.
![]()
![]()
Table 5. Toda-Yamamoto Granger non-causality test.
Note: (.) are p-values; ***, ** and * indicate the rejection of null hypothesis at 1%, 5% and 10% significance, respectively.
![]()
Table 6. Summary of direction of causality between variables.
Note: ***, ** and * indicate the rejection of null hypothesis of no-causality at 1%, 5% and 10% significance, respectively.
As we can notice on the above table, the following relations are established among the variables: unidirectional causality, bi-direction causality or feedback relationship and no causality among the variables. At the aggregated level, there is an unidirectional relationship running from primary energy consumption to CO2 emissions in Algeria and South Africa, and a feedback or bi-directional relationship between primary energy consumption and CO2 emissions in Egypt. Bi-directional causality is also found between carbon emissions and GDP per capita is Egypt and South Africa, and a unidirectional relationship running from economic growth to CO2 emissions in Algeria. Finally, there is a feedback relationship between energy consumption and GDP per capita in Algeria, Egypt and South Africa. Overall, these results indicate that the reduction in primary energy consumption will have cut down carbon emissions and slow down economic growth since there is a feedback relationship between energy and economic growth. At the disaggregated level, except the case of Algeria where there is no relationship between economic growth and coal consumption, other result show several forms of causal relationship between disaggregated energy variables, economic growth and energy consumption.
4. Conclusions and Policy Implications
This paper investigated the effect and the causal relationship between economic growth, energy consumption and carbon emissions in the top three emitters in Africa over the period from 1971 to 2015. The Zivot and Andrews [38] unit root tests were applied in order to endogenously control for any structural breaks in the time series, and the bounds testing approach to cointegration helped to check for the existence of long run relationship between our variables. The empirical results show that economic growth and aggregate energy consumption, measured by primary energy consumption, have a positive and significant impact on CO2 emissions both in the long and short run. At the disaggregated level, we find that results oil, electric power consumption and coal consumption are the more polluting energy sources in Algeria, Egypt and South Africa, respectively. Furthermore, the results show that urbanization has a positive impact on carbon emissions; even if the impact is not significant in all the countries. Lastly, the role of trade openness is mixed, depending on the country. In addition, the Toda-Yamamoto [24] Granger non-causality test showed several relationships among economic growth, energy consumption and carbon emissions, each one affecting other.
As policy recommendations, we suggest to governments of Algeria, Egypt and South Africa that they should implement and/or reinforce existing policies related to energy efficiency (existing policies include the National Programme for the promotion of renewable energy until 2020 in Algeria, the Renewable Energy Strategy in Egypt, the Integrated Resource Plan in South Africa). It is also recommended to develop integrated energy plans with the aim to substantially increase the contribution of renewable energy production and consumption in the energy mix. In addition, population growth and urbanization will require additional investments to improve energy efficiency in the public transport networks, building and industrial sector. Such measures could generate a double dividend phenomenon, by firstly sustaining the long run economic growth rate; and secondly by mitigating the adverse effect of energy consumption on CO2 emissions. An interesting way to extend this study would consist of analyzing the impact of other renewable energy consumption (wind, solar and biomass) on carbon emissions in these countries. Presently, there are very limited data on these variables.
List of Appendices
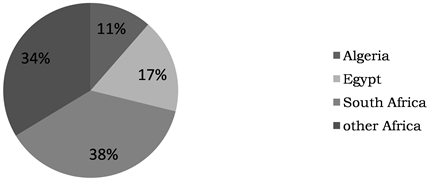
Appendix 1. Carbon emissions profile in Africa in 2015. Source: Authors, from IEA [8] .
Appendix 2. Descriptive statistics and correlation matrix.