1. Introduction
The idea of calculating the genetic code arose after many years of research on mathematical genetics. The basic idea was that the code, apparently, today―half a century after its discovery, can be calculated on the basis of experimental data already known to date. The approach proposed below is not the main, or comprehensive, and it can only be considered as one of the attempts to find an approach to the solution of the task. After all, it’s about finding a solution in a complex structure that describes the main characteristics for almost all existing living organisms.
Each new century put forward ever new tasks of both theoretical and applied mathematics. In this paper, we consider the newest problem of discrete mathematics, which could be put only in the 21st century. This task belongs to the field of biomathematics, because biology and related tasks are key in the present century. In the world there is no such kind of publications on this topic; therefore this work can be considered as the world’s first full version of the work on the calculation of the genetic code.
First of all, the question arose: What sets can be used in this case. Our approach was based on the search for all codes satisfying the set of amino acids that record overlapping genes. The author has studied the subject matter of the mathematical analysis of such genes for a number of years [2] , and it was this analysis that led to the formulation of this problem. From the very beginning it was clear that the discussion would mainly focus on the iterative process. Since overlapping of genes contains two, three, etc., amino acids, right up to 6, the first task was to find those overlaps where the same amino acid participates (in overlaps, it participates with different encodings, according to the genetic code). On this occasion, a special study was conducted.
2. Theorem for Homogeneous Overlaps
We consider unusual ways of recording genetic information-overlapping genes, when the same DNA portion corresponds to more than one protein. We investigated all 5 possible cases of overlapping of genes resolved by DNA structure, which were studied earlier [5] . This study was based on a mathematical analysis of all 5 possible overlap cases and relied on sets of so-called elementary genetic overlaps-e.o., or overlaps corresponding to a pair of single amino acids. In [6] a brief analysis of such sets is presented, and the final version in [2] . In Figure 1. A description of the structure of the sets W1-W5 is presented, and are presented by the 4th e.o. In each of these sets.
The principal position of this research is indicated in [2] , where it was shown that the presented list of elementary overlaps can cost any (!) Allowed by the structure of the genetic code, overlapping not only 2 but also all admissible overlap from 3 to 6 Genes. The urgency of the problems is due to the current situation: overlapping genes common in viruses, mitochondria, bacteria and plasmids were found is in eukaryotic of large genomes, including humans, with the number of overlaps usually high, for the human genome it is about 1700 [7] .
In the mathematical analysis of overlaps of more than two genes, we have investigated some problems. Of course, it would be possible to construct sets of all e.o. From 3 to 6 genes. It is not difficult to do this with the help of modern computer facilities. However, the main thing-what new conclusions-it can give. And that’s why we are going the traditional way-from tasks. Let us first briefly discuss only some of them, solutions for which we have already published. The first of these concerns the analysis of ambiguities [8] [9] [10] , this is when two
![]()
Figure 1. Description of the structure of sets W1-W5. There are 4 e. In each of the sets. The total number of e.o. In the corresponding set.
encodings correspond to the same pair of amino acids (see the example below). Another problem was connected with the construction and analysis of a set of elementary overlaps for 3 genes overlapping in the same DNA chain. It is established that there are only 307 such overlaps. On the basis of these overlaps, a new problem was posed, connected with the calculation of the genetic code by mathematical methods [11] [12] . The question of why exactly such a set was chosen to calculate the code was based on a theorem that was published relatively recently [4] . We are talking about the calculation and analysis of all homogeneous e.o.ochs. From 2 to 6 genes. Are e.o. which correspond to the same amino acid. Its solution is given by the following theorem.
We call an e.o.-elementary overlap for i amino acids, where, iÎ(2,6). Thus, the e.o. introduced earlier in [2] . Will be referred to as e.o.-2. Figure 2 shows the general representation for e.o.-6.
For the amino acid Ama (isolated by hatching) encoded by the triplet n1n2n3, there are 5 alternative amino acids Ama1-Ama5, the encodings of which are formed by −1, +1 shifts in the same DNA chain (→) and −1, 0, +1 in the complementary DNA strand (←). The designations ni, iÎ(0,4) are the nucleotides from the set A, T, C, G; N
iÎ(0,4)-complementary components: i.e. For
i = A; ni = T; ni = C,
= G for any iÎ(0,4) and vice versa. In order to sequentially isolate e.o.-2 for all 5 cases of pair overlaps from [2] [3] , in Figure 3 one should
![]()
Figure 2. General presentation for e.o.-6. (See the text). -5 e.o.-2 for overlaps from one DNA chain.
![]()
Figure 3. (a) For amino acid Ama, encoded by the triplet n1n2n3, there are 2 alternative amino acids Ama1 and Ama2. Their encodings are formed by −1, +1 shifts in the same DNA (®) chain. The codon n0n1n2 for Ama1 overlaps with codon n1n2n3 for Ama-the overlap contains two nucleotides n1n2; The codon n2n3n4 for Ama2 overlaps with codon n1n2n3 for Ama-the overlap contains two nucleotides n2n3. As a result, the triple overlap contains only one common position n2. (b) Elements of sets of combinations of amino acids, formed on the basis of elementary overlap from Figure 3(a). On the left there is one element of the set U1, in the center there are two elements of the set U2 and to the right one element of the set U3.
consistently leave one of the 5 pairs of amino acids: (Ama, Amai), iÎ(1,5). In order to sequentially isolate all overlap cases for e.o.-3 in Figure 3, it is necessary to leave Ama and a pair of amino acids out of 5 possible ones or we have 10 cases of triple overlap, etc. We turn to the search for a homogeneous subset for all possible e.o.-2-6, or subsets, in each e.o. Which is the same amino acid. We denote it by W2-6. To represent homogeneous elementary overlaps, the following notation is used: Y: T, C; X: A, G; N: A, G, C, T.
Occurs
Theorem. The homogeneous subset e.o.-6 contains only 31 e.o. which belong only to the sets of e.o.-2-e.o.-3, of which:
-5 e.o.-2 for overlaps from one DNA chain:
 (1)
(1)
-19 e.o.-2 for overlaps from various DNA chains:
 (2)
(2)
-4 e.o.-3 for overlaps for overlaps from one DNA chain.
 (3)
(3)
-3 e.o.-3 for overlaps from various DNA chain
 (4)
(4)
We give a comment on the statement of the theorem. Cases 22.1 and 22.2 correspond to the same amino acid Ser-Ser; This is one of six ambiguities, which was established earlier [9] . It follows from the theorem that there are no homogeneous e.o.ic forms, more than the third order, or e.o.-4-e.o.-6. To prove this fact, we note that all the enumerated e. From (1)-(4) have one common property. It consists in that the amino acid encodings in each of these overlaps are present in the shifted phases-shifts by −1 or +1 nucleotide, and regardless of the DNA strand or not, there is not one e.o. where the pair of overlapping codons would be in one and The same phase.
It follows from (2) that similar e. There are no overlaps from different DNA chains, so they are not possible in the structures of homogeneous e.o 4-e.o. 6
For amino acid Ama (highlighted by hatching), encoded by the triplet n1n2n3, there are 5 alternative a
Introduction of basic sets
As follows from the previous section, homogeneous elementary overlaps occur only for overlaps with participation of not more than three amino acids. To select working sets, consider all such overlaps.
First of all, it is necessary to exclude from consideration all homogeneous overlaps in which two strands of DNA participate. Consideration of these overlaps requires the introduction of a double strand of DNA-this is an additional condition in the problem. Eliminating such homogeneous overlaps, we proceed from the principle of constructing an algorithm with a minimum number of conditions. Therefore, in our examination there remain only homogeneous overlaps belonging to the same DNA chain: for pairs of amino acids (1), there are only 5 of them and similar overlaps for three amino acids (3)-th total of 4. Thus, we selected the main working sets E.o., namely, those in which these homogeneous overlaps are present. The final version of these sets is presented on pages 312-319 in [2] .
Let us consider the question in more detail. On sets with these overlaps. Earlier [2] we introduced the notion of elementary overlap with respect only to overlapping pairs of genes. Let’s generalize this conce.o.t for three genes belonging to the same DNA chain. By the term elementary overlap, we mean the overlap for the codons of single amino acids by the maximum number of positions. Figure 3(a) for the amino acid Ama encoded by the triplet n1n2n3 indicates the alternative amino acids Ama1 and Ama2, the encodings of which are n0n1n2 and n2n3n4, respectively, are formed by shifts of −1 and +1 nucleotides in the same DNA (®) chain. It is assumed that all the values of n0-n4 belong to the canonical set of four nucleotides. On the basis of Figure 3(a), it is possible to construct three types of combinations of amino acids, re.o.resented in Figure 3(b) and designated respectively u1, u2, u3: one u1 for overlapping one position, two u2 for overlapping in two positions, and one u3 for overlapping 3 Amino acids
In Figure 4 and Figure 5 only fragments of these sets are presented, and some of their characteristics are presented in Table 1.
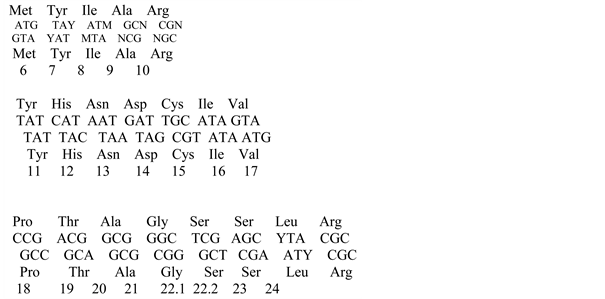
Amino acids shown in Table 1. Elements are given in the view that is used in this task. Each of the elements consists of three lines: upper, middle and lower. The named amino acids Met and Arg are shown in the middle line.
Formulation of the problem. Introduction of a compressed set.
FORMULATION OF THE PROBLEM. Let’s have a set of 4 letters: N: a, b, c, d, and also triplets-any triples of these letters, there are 64 in all. Moreover, each of the 20 canonical amino acids can be encoded by an arbitrary combination of such triplets. The task is to search for all the genetic codes that correspond to
![]()
Figure 4. A list of some elements of the set U2 is given. These are two sets of such elements corresponding to the first-Met and the last-Arg amino acids from the corresponding set, represented in the first column of Table 1. Each of the representation contains two lines: the first corresponds to a shift between codons equal to −1, and the second corresponds to a +1. Under the name of the amino acid, the number of elements corresponding to these shifts is indicated, and the lower numbers correspond to the numbers in the full list of these elements.
![]()
Figure 5. The elements with numbers 1-8 and 279-307 from the set U3, corresponding to the first (Met) and last (Arg) amino acids from the list.
all the elements designated above the three sets U1, U2, U3, corresponding to the genetic experiments.
![]()
Table 1. Some data of sets U2 and U1 for amino acids Amai, i (1,20).
Notation. The first 4 columns indicate the number of overlaps, and in parentheses the list of amino acids for overlaps: 1 and 2. Bases (m12), on 2 and 3 bases (m23) on 1 base with the third base (m1-3), on 3 bases with the first base. (M3-1). Columns 3 and 4 refer only to overlaps with Lys, Phe, Pro, Gly, so this number can not be more than 4; .: Х: а, d; Y: b, с; М: а, b, с; N: а, b, с, d.
For the future, we use standard three-letter abbreviations for each of the 20 amino acids.
In [11] we talked about ste.o.s to calculate this problem, but did not say how the required elements were selected at the ste.o. For such a selection, a special representation of the basic working set was introduced. This result is published in detail for the first time.
We introduce one concise representation for 307 elements of the principal set-U3. In Figure 6, for each Ama of this set (it is indicated in the corresponding cell), the amino acid Ama1 is plotted along the abscissa axis, and the ordinate is Ama2 (see Figure 3(a)). It turned out that the resulting representation is not homogeneous, but contains multiple ambiguities: these are cases when more than one Ama value corresponds to the same Ama1 and Ama2 values. It turned out that the number of ambiguities in the range from 2 to 4. All these cases are shaded in Figure 6 and they are denoted by A1-A13, and their decoding is given in the caption to this figure.
It should be noted that these ambiguities correspond to the values of Ser, Leu,
![]()
Figure 6. The compressed representation for 307 elements of the main set-U3: for each Ama of this set (it is indicated in the corresponding cell) is given the Ama1 amino acid along the abscissa axis, and on the ordinate axis-Ama2 (see Figure 1(a)). It turned out that the resulting representation is not homogeneous, but contains multiple ambiguities: these are the cases when more than one Ama value corresponds to the same Ama1 and Ama2 values-from 2 to 4. These cases are shaded in this figure, they are denoted by A1-A13, i.e. there are only 13 of them, although the figure shows 34 hatchings. The fact is that in this figure A6, A9 and A10 are represented 4 times, A1, A5, A7, A8 and A11―three times, A3 and A4―2 times, and A2, A12 and A13―only by one time. We have A1 Gln, Leu; A2: Gln, Val, Leu; ...A13: Gln, Pro, Ala.
Arg, both along the abscissa axis and along the ordinate axis. However, the most significant area in Figure 6, which corresponds to the cases where on both axes there is none of the amino acids from the Ser, Leu, Arg. For our calculations, the last region is reduced, eliminating from it all cells containing Ser, Leu, Arg. In Figure 7, the shading corresponds to the three amino acids mentioned, and the non-zero elements of the unshaded region have the following property: each Ama value is unique for the corresponding pair Ama1 and Ama2.
The above property allowed us to refer to the first stage of the calculation, when the calculation of the encodings for all elements is made Ama value on the basis of the encodings for the corresponding pair Ama1 and Ama2. The results of the ste.o.-by-ste.o. solution of the problem are presented in Table 2, but the most important stage of the study was the question of finding the initial approximation.
The initial approximation
THE SOLUTION OF THE PROBLEM. We use the standard three-letter abbreviations for each of the 20 amino acids listed in the first column of Table 1. We have a set
A0: Amai, iÎ(1,20). (5)
We introduce the definition. Let us turn to the previously introduced homogeneous overlaps. As before, we call a combination of amino acids, constructed on the basis of an elementary genetic overlap, homogeneous if the same amino acid participates in it. For homogeneous elements of the set we have.
Property. Let the encodings Ama for homogeneous u3 have one of the fol-
![]()
Figure 7. The reduced region of Figure 6: there are areas in which the code is calculated. All the shaded regions are cut off for the reasons indicated above, and the main area in the calculation is re.o.resented without shading.
![]()
Table 2. Steps 1-9 of the iterative process of calculating the genetic code. The last line indicates the number of calculated codons after this step. Notation: Х: а,d; Y: b, с; М: а, b, с;N: а, b, с, d.
lowing three representation:
n1N1N2, N3n2N4, N5N6n3, (6)
Where small letters denote the unit components of the set N, and large-some subsets of this set, up to N. Then homogeneous u3 can exist only if at least one base triplet or triplet with three identical letters is used.
For the proof we successively substitute each of the representation (6) in u3:
 (7)
(7)
where n'i is the single component of the set Ni, where iÎ(1,6), and the string na.-nucleotide sequences that are formed after this substitution. In the first case, in (3), the base codon n1n1n1 was used for encoding amino acid Ama from the bottom position, in the second-n2n2n2-from the middle position, and in the third-n3n3n3-from the top position.
We turn to homogeneous u3 from the set U3, which turned out to be 4:
 (8)
(8)
Within the framework of the assumption specified in the Property, the following ste.o.-by-ste.o. process of searching for a genetic code is proposed; See Table 2. Ste.o. 1. Amino acids from (8) will assign the corresponding base codons. This assignment is not unique. However, in our approach, the set of letters N: a, b, c, d is not correlated with the canonical set of 4 nucleotides; This will be discussed at the end of the paper. Therefore, we will continue to operate with only one of the representation for the amino acids from (4), which we assign respectively the following basic triplets:
Lys: aaa, Phe: bbb, Pro: ccc, Gly: ddd (9)
For further calculations, we turn to some generalized data on the sets U2 and U1, which are given in Table 1.
Step. 2. From Table 1 it follows that, as in column m12 (the number and the list of overlapping amino acids on 1 and 2 bases are indicated), and in column m23 (similar data for 2 and 3 bases) do not contain mutual overlap between amino acids from (8). Such overlaps take place only one position and belong to the set U1. We have:
 (10)
(10)
where the first 4 elements of u1 correspond to overlaps for 3 positions (in parentheses the alternative variants are indicated, see column m3-1 from Table 1), the next 4-overlaps for the first positions (see column m1-3). The formal substitution of the base codons from (9) into (10) leads the encodings of all 4 amino acids to the fact that they become ambiguous in the 1 st and 3 rd positions. For the sake of clarity, we present the derivation of just two amino acids from (9)- Lys and associated with it according to the first overlap of (10)-Gly. According to the above, we have: Lys should be encoded by a set of triplets X1aX, and Gly- X1dN, where X1: a, d, c; X: a, d. Then there is an overlap of Lys with Gly in two positions, which is impossible according to Table 1. It also does not allow two other possibilities: Lys can not be encoded by a set of triplets X1aa if Gly is ddN, and also Lys can not be encoded by a set of triples aaX if Gly is X1dd. There are still two possibilities: both Lys and Gly are coded by ambiguous codons for the same positions. The case of Lys: X1aa, Gly: X1dd encoding is impossible, as the condition in Table 1 can not be satisfied: the number m23 for Gly is 5 according to Table 1. (And for a similar encoding Gly there can be a maximum of −4). Therefore, there remains the only possible option for the encodings in question, when there are ambiguities in the third position. Similarly, you can set the encoding for the remaining Phe and Pro pairs. In the end, we get:
Lys: aaX, Phe: bbY, Pro: ccN, Gly: ddN, (11)
From Table 1 it follows that the value of m12 does not exceed the number 4 for the amino acids from (5) with the numbers from 1 to 17. The number 4 means that the first and second positions can be single-valued, which can not be said for m12 for Ser, Leu, Arg, for which these values are 7.8.7, respectively. Therefore, in the next ste.o.s 3-7 only amino acids from (5) with numbers up to 17 will be considered. Note that the calculation of the encodings for all amino acids from (5) is carried out according to the method published in [3]
3. Step 3-by-Step 7 Calculation in the Uniqueness Domain
The solution search in step 3 is illustrated in Figure 8 (step. 3), where the reduced unambiguity region is presented. For each of the four amino acids from (9) we carry out two bands (gray hatching in Fig.) for Ama1 (horizontal strip, Figure 3 outside the figure indicates the step. number) and Ama2 (vertical strip). As a result, at the intersections of these bands we find only 4 amino acids: Gln, Glu, Val, Ala, and taking into account the accepted standard record and the codings from (9)
 (12)
(12)
where n.s. is the nucleotide sequence. From (12) we have single-valued encodings for 4 amino acids: Gln, Glu, Val, Ala, and with (9) we find:
Gln:caX, Glu:daX, Val:dbN, Ala:dcN, (13)
Thus, it is shown that the use of the introduced reduced set leads to minimal costs in the ste.o., compared to a direct search for 307 elements of the main set-U3.
Step 4. The solution is explained in Figure 8 (step 4), where the Figure 4 outside the figure indicates the new bands corresponding to the solution from (13), namely the bands for Gln, Glu, Val, Ala. As a result, we have three overlaps:
![]() (14)
(14)
On the basis of which we obtain
Trp: bdd, Cys: bdY (15)
Step 5. In the set U3 there are no elements that have two amino acids from the sets (11), (13), (15): all the bands for the Figure 5, which are indicated outside the figure, do not have any required intersection. In connection with this feature, we turned to the set U2 and consider one of the admissible possibilities. This possibility was not accidental: it had the maximum number of overlaps in comparison with other cases. As a result, on the basis of two elements u2 we have:
![]() (16)
(16)
We get two encodings for Thr: xca, xcc, where x- is not yet known. To find all the encodings for Thr, let’s look at its values m1-3 and m3-1. From equality m1-3 = 3 (Lys, Pro, Gly) it follows that x can take no more than two values: a, d, since in the listed set there is no Phe. However, the value of d is impossible, because Dca and dcc are Ala encodings. In addition, from the equality m3-1 = 4 (this means that the first positions of the 4 amino acid encodings: Lys, Phe, Pro, Gly overlap with the encodings of the third Thr position), the third position in the Thr encoding is equal to N. Thus, we have:
Thr: acN. (17)
Step 6. In Figure 8 (step. 6), after inserting the bands 6 corresponding to Thr along the vertical and horizontal lines, four amino acids were identified in bold: 3 times Asn, once Tyr, 3 times His and once Asp. These amino acids correspond to the overlap:
![]() (18)
(18)
On the basis of which we calculate four encodings for Tyr: bac, Asn: aac His: cac, Asp: daс. Taking into account the data from column m3-1, we finally find:
Tyr: baY, Asn: aaY, His: caY, Asp: daY (19)
Step 7. For these amino acids we conduct 4 bands horizontally and vertically, respectively. At the same time, only two amino acids-Met and Ile-were found in 8 positions, see the bold font in Figure 8 (step 7).
Let us single out two overlaps,
![]() (20)
(20)
Which were sufficient for calculation. Taking into account the data from column m3-1, we finally find:
Met: abd, Ile: abM, (21)
where M: a, b, c
Step 7 finishes the search for encodings for the entered uniqueness domain- they turned out to be 43 for the first 17 amino acids; they are given in Table 2. The further calculation was reduced to the search for solutions for Ser, Leu, Arg present in the compressed set of Fig.
4. Search for a Solution in the Field of Ambiguity
Step 8. Finding solutions in an area where the values of Ama1 and Ama2 belong not only to these 17 amino acids. On the basis of Figure 7 we get
![]() (22)
(22)
From these overlappings we find the following encodings:
Ser: bca, bcc, adY; Leu: cbX, cbb, bbX; Arg: cdN, adX. (23)
Step 9. From the ambiguity region in Figure 2, we select cases containing two amino acids from the set Ser, Leu, Arg and giving solutions different from (23). We have:
![]() (24)
(24)
From the first and second overlap we find: Ser: bcd, bcb, and from the third- Leu: cbc. The final encodings for Ser, Leu, Arg are presented in Table 2. And the total number of semantic triplets for all 20 amino acids from in this table is 61. An additional check shows that all elements of the ambiguity region do not contain any other solutions. Three triplets: baX, bda are not defined when using any elements of the sets U1, U2, U3; they supplement the total number of triplets to 64.
When passing from the set of letters a, b, c, d to the canonical nucleotides A, C, T, G, 24 similar genetic codes can be obtained. Only one of them is standard, with a = A, b = T, c = C, d = G, and triplets baX, bda become TAA, TAG, TGA; they play a role terminator codons-codons, stopping protein synthesis.
Acknowledgements
The author thanks a brilliant interpreter O. N. Kozlov, who translated this text from Russian.
Funding
The work was supported by Russian Foundation for Basic Research (project codes 16-01-00018, 17-01-00053).