An Index Assessing the Energetic Complementarity in Time between More than Two Energy Resources ()
1. Introduction
The maintenance of an adequate energy supply of a region relies on how its energy grid is composed, taking into account the existence and availability of a set of energy sources. The output of each individual source over a period of time varies, due to the seasonality of the natural sources (hydraulic, wind and solar) or by activating or deactivating thermal generators (from fossil fuels or biofuels) that make the system.
For a given energy demand, verifying how the natural sources available complement each other is a point of interest, because from this complementarity it is possible to assess the need of thermal complementation of the system, an option that is always more expensive and generates more pollution [1] [2] .
Large interconnected systems must have the energy dispatch established based on regional differences in demand and instantaneous availability of energy. At certain times, the differences between demands and availabilities can be attenuated considering the possible complementarity between the energy resources [3] .
When considering the design of the energy grid of a region, measuring the complementarity between sources is also useful, even if the sources are not yet installed. This measure can help the decision making for new investments, choosing the more appropriate sources for each region, taking into account the robustness of the energy grid and the operational costs involved, in order to fulfill the expected demand.
The work of Beluco et al. [4] proposed a way to evaluate the complementarity in time in the same place with the determination of a dimensionless index. Later, this index was crossed with performance information [5] and allowed to know how the performance of hybrid systems can be directly influenced by the complementarity.
The work of Beluco et al. [4] [5] [6] established the concept of complementarity in time in the same place as being composed of three components: a partial time-complementarity, anenergy-complementarity and anamplitude-complemen- tarity. The calculation is performed based on average values and minimum and maximum values.
The index proposed by Beluco was applied by Pianezzola [7] in the preparation of complementary maps1 of wind and solar energy throughout the state of Rio Grande do Sul. Bagatini [8] also developed complementary maps2 for hydro, wind and solar energy, considering these features two by two, For the State of Rio Grande do Sul. Eifler [9] applied the Beluco index to evaluate the complementarity of wind and solar energy throughout the Northeast region of Brazil.
Cantão et al. [10] evaluated the energetic complementarity between water and wind resources along the Brazilian territory, presenting the results through maps of corelation. This work evaluated both the energetic complementarity at the same locationand the emnergetic complementarity considering distinct locations.
This paper proposes an alternative method for calculating time complementarity. This method allows the determination of the complementarity between two or more energy resources. This method also allows the calculation to be performed based on hourly or daily series and not only based on maximum and minimum values.
As an application of the proposed method, a map with the energetic complementarity in time between hydropower, wind energy and solar energy for the Brazilian State of Rio Grande do Sul is presented.
2. Complementarity Index Proposed by Beluco et al. (2008)
Beluco et al. [4] [5] [6] defined complementarity between renewable energy resources (in particular, solar and hydraulic) as the ability of the sources to work in a complimentary way. They defined a complementary index 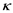 as shown in Equation (1), where
as shown in Equation (1), where ,
, 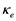 ,
, 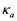 are partial indexes measuring complementarity with respect to time, energy and amplitude, respectively.
are partial indexes measuring complementarity with respect to time, energy and amplitude, respectively.
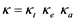 (1)
(1)
The time-complementary index is defined as shown in Equation (2), where maximum and minimum availability of hydraulic energy occur, respectively, on Julian day number 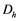 and
and 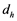 (likewise
(likewise 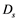 and
and 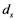 refer to the same days regarding solar energy). Note that if the differences
refer to the same days regarding solar energy). Note that if the differences 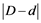 equal 180, then
equal 180, then , so that
, so that 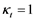 if the maxima are 180 days apart, and
if the maxima are 180 days apart, and 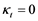 if the maxima coincide.
if the maxima coincide.
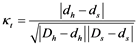 (2)
(2)
The energy-complementary index is defined as shown in Equation (3), where the total yearly hydraulic and solar energies are given  and
and , both positive, so that
, both positive, so that  if
if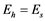 , and
, and ![]() vanishes if
vanishes if ![]() tends to zero or infinity (that is, both sources are greatly disproportional).
tends to zero or infinity (that is, both sources are greatly disproportional).
![]() (3)
(3)
Finally, the amplitude-complementarity index is given by previously defining the following difference score relating energy values of a given source, as shown in Equation (4), where![]() ,
, ![]() and
and ![]() are, respectively, the maximum, minimum and average value for the energy availability for the given source.
are, respectively, the maximum, minimum and average value for the energy availability for the given source.
![]() (4)
(4)
The index is defined as shown in Equation (5), where ![]() and
and ![]() are the difference scores for hydraulic and solar power, respectively. As it can be readily verified, the two piecewise expressions for
are the difference scores for hydraulic and solar power, respectively. As it can be readily verified, the two piecewise expressions for ![]() are reciprocals of one another.
are reciprocals of one another.
![]() (5)
(5)
Note that all three partial indexes are defined for two sources only and are based in a few parameters, like maxima and minima and the points in time where they occur. On this work, we give a new definition of the complementarity index that takes into account the whole behavior of each source, as well as allowing for any number of sources.
3. A Complementarity Index for More than Two Energy Resources
Suppose that ![]() are nonnegative functions defined in
are nonnegative functions defined in ![]() that describe the rate of availability of energy (that is, power) in a region along a certain time interval; so
that describe the rate of availability of energy (that is, power) in a region along a certain time interval; so ![]() is the total generated power. So the average power is defined by Equation (6).
is the total generated power. So the average power is defined by Equation (6).
![]() (6)
(6)
Note that the integral is the total energy provided in the period, and it is equal to![]() . The contribution of each individual source may vary over time, but if the total energy provided by the combination of the sources is constant, then those sources are said to have perfect complementarity.
. The contribution of each individual source may vary over time, but if the total energy provided by the combination of the sources is constant, then those sources are said to have perfect complementarity.
The area between ![]() and the function with constant value
and the function with constant value ![]() value represents a energy gap, so the area below the minimum of the two curves may be seen as a measure of how far below average is this power. Thus, we define the complementarity index
value represents a energy gap, so the area below the minimum of the two curves may be seen as a measure of how far below average is this power. Thus, we define the complementarity index ![]() as shown in Equation (7). This formula can be interpreted as the ratio between the generated energy, discarding excess (above average) power, and the overall generate energy.
as shown in Equation (7). This formula can be interpreted as the ratio between the generated energy, discarding excess (above average) power, and the overall generate energy.
![]() (7)
(7)
As all values involved are nonnegative, and because the integral is limited by![]() , we have
, we have![]() . The bounds are tight; the upper bound is attained by any combination of functions with constant sum; for the lower bound, for any
. The bounds are tight; the upper bound is attained by any combination of functions with constant sum; for the lower bound, for any![]() , let
, let ![]() for
for ![]() and 0; a simple calculation show that
and 0; a simple calculation show that![]() .
.
This formulation of the index as a definite integral allows for the use of discrete series of data, without the need of regression. For example, if we consider
series of ![]() equally spaced data points each, being
equally spaced data points each, being ![]() the j-th entry of the da i-th series, we may define the discrete version of the index as shown in Equation (8).
the j-th entry of the da i-th series, we may define the discrete version of the index as shown in Equation (8).
![]() . (8)
. (8)
4. Two Examples of Application of the Proposed Index
In this section, we illustrate the calculation of ![]() under this new definition on two special cases involving two sources. In the first example, we have two sinusoidal curves of period equal to 1. In the second, we have two step functions, also with period 1. Note that, under the previous definition [4] , it is not clear how to proceed in the second case, as the Julian day numbers where the maxima or minima occur are not unique.
under this new definition on two special cases involving two sources. In the first example, we have two sinusoidal curves of period equal to 1. In the second, we have two step functions, also with period 1. Note that, under the previous definition [4] , it is not clear how to proceed in the second case, as the Julian day numbers where the maxima or minima occur are not unique.
Let ![]() and
and![]() , that is, two sinusoidal curves with period 1 with a phase difference equal to
, and
, that is, two sinusoidal curves with period 1 with a phase difference equal to
, and ![]() the total provided power. If
the total provided power. If![]() , at each time, the excess of one source perfectly complements the shortageof the other, so that the sum of these two functions is the constant function 1, that is, there is perfect complementarity between the two energy resources.
, at each time, the excess of one source perfectly complements the shortageof the other, so that the sum of these two functions is the constant function 1, that is, there is perfect complementarity between the two energy resources.
Otherwise, there will be a gap between ![]() and the average power, as seen for instance in Figure 1. As
and the average power, as seen for instance in Figure 1. As ![]() goes down towards 0 or up towards 1, this gap increases. Figure 1 illustrates the case where
goes down towards 0 or up towards 1, this gap increases. Figure 1 illustrates the case where![]() . The value of the index (
. The value of the index (![]() ) corresponds to the area below the thick line. The gap is the area between the thick line and the dashed line.
) corresponds to the area below the thick line. The gap is the area between the thick line and the dashed line.
Now we deduce an expression for this special case as a function of the phase constant![]() . Using the classical relation to
. Using the classical relation to![]() , we get Equation (9).
, we get Equation (9).
![]() (9)
(9)
For![]() , we have
, we have ![]() if
if![]() . So the gap is given
. So the gap is given
![]()
Figure 1. Graph of f (in red line), g (in blue line), p (in thinner black line) and k (in thicker black line) for d = 0.25.
by Equation (10). The calculation for ![]() is analogous by symmetry.
is analogous by symmetry.
![]() (10)
(10)
Therefore, Equation (11), which minimum value is
![]() . Figure 2 illustrates the calculation of
. Figure 2 illustrates the calculation of![]() .
.
![]() (11)
(11)
This example shows how easy it is to extend this new concept of complementarity to a case with three energy resources. It would suffice to include in this reasoning a third sine function. Obviously a case more complex and with more breaks in analysis, but still simple to be understood.
Let ![]() and
and![]() , both with period 1 with a phase difference d. Note that
, both with period 1 with a phase difference d. Note that ![]() if
if ![]() (almost everywhere) and 0 otherwise. Again, the complementarity is perfect if
(almost everywhere) and 0 otherwise. Again, the complementarity is perfect if![]() , and get worse as
, and get worse as ![]() goes to 0 or 1.
goes to 0 or 1.
Figure 3 illustrates the case where![]() . For
. For![]() , we can write
, we can write ![]() as shown in Equation (12), so that the gap height is equal to 1 if
as shown in Equation (12), so that the gap height is equal to 1 if ![]() and equal to 0 otherwise.
and equal to 0 otherwise.
![]() (12)
(12)
![]()
Figure 2. Graph of f (in red line), g (in blue line), p (in thinner black line) and k (in thicker black line) for d = 0.00.
![]()
Figure 3. Graph of f, g (step functions) and p for d = 0.25.
Therefore, the gap is calculated with Equation (13).
![]() (13)
(13)
The calculation for ![]() is analogous, by symmetry. Therefore, Equation (14), which minimum value is
is analogous, by symmetry. Therefore, Equation (14), which minimum value is![]() .
.
![]() (14)
(14)
5. A Complementarity Map Drawn up with the Proposed Index
This section describes the method for determination of cmoplementarity and presents a map containing values of the complementarity index for three energy resources throughout the State of Rio Grande do Sul, the southernmost state of Brazil. The three resources considered were hydropower, wind and solar energy. Figure 4 shows this map.
Hydrological flow data were obtained from the HydroWeb website [11] , maintained by the Brazilian National Water Agency. Daily flow data of 14 fluviometric stations throughout the State, in Bagé, Bento Gonçalves, Bom Jesus,Caxias do Sul, Cruz Alta, Encruzilhada do Sul, Iraí, Lagoa Vermelha, Pelotas, Porto Alegre, Rio Grande, Santa Maria, São Luiz Gonzaga and Uruguaiana, were obtained.
![]()
Figure 4. Energetic complementarity in time for hydro, wind and solar energy resources along the State of Rio Grande do Sul, the southernmost state of Brazil.
Wind speed data were obtained from the BDMER [12] site, maintained by INMET. The solar radiation data were obtained using the software Homer [13] [14] [15] , in a database of NASA. Time series of wind velocity and solar radiation were obtained for the same locations of the flow series.
The data were manipulated as suggested by Beluco et al. [4] and the values of the time-complementarity index given by Equation (8), were calculated for the fourteen municipalities for which the data series were obtained. A map was elaborated to know the distribution of this index throughout the State of Rio Grande do Sul.
The map shows better complementarity in time results among the three energy resources cited in the Northeastern region, and also a reasonable complementarity in the South. The central region of the State, as well as the region to the west, presents intermediate values of energetic complementarity in time.
6. Conclusions
This paper presented a new method for calculating energy complementarity over time which has advantages over previous methods. The proposed method allows determining the complementarity between two energy resources and also allows determinig complementarity between more than two energy resources. In addition, the proposed method still allows the use of hourly or daily series and not only average values and maximum or minimum values.
As an application of the proposed method, a map indicating the energetic complementarity in time between hydro, wind and solar energy throughout the State of Rio Grande do Sul, the southernmost state of Brazil, was built. This map shows that the northeast part of the State presents better complementarity and that the central and western regions present intermediate values of complementarities.
Acknowledgements
The authors would like to thank the support of the Institute of Mathematics of UFRGS for projects and research activities related to renewable energy resources. The authors also thank the environmental engineer Marcos Bagatini and Professor Alfonso Risso for the support to elaborate the map presented in Figure 4.
NOTES
*Results were partially presented inCongresso de Matemática Aplicada e Computacional do Sudeste, 2015.
1This work of Pianezzola resulted in a paper published in this Special Issue on Energetic Complementarity.
2This work of Bagatini also resulted in a paper published in this Special Issue on Energetic Complementarity.