Performance Assessment of a Calm Flapping Wind Turbine with Small Attack Angle ()
1. Introduction
Facing the future challenge in energy demands, renewable energy is considered as the main source of sustainable energy. An interest in utilizing renewable energy is growing rapidly owing to several factors such as cost-competitiveness, energy security, environmental concerns, growing demand for energy in developing countries and emerging economies with the need for access to modern energy. In 2015, an estimated of 147 GW renewable power capacity was added, which is the largest amount ever [1] .
Wind energy is considered as a viable renewable source of green energy for a sustainable environment. Natural energy of “wind” in the wind power is converted into electrical energy without any of the CO2 emissions. In addition, the produced energy easily adds into the grid of the building with reduction of its external energy demand [2] . A new Carbon Trust study [3] showed that small wind turbines could generate up to 1.5 Terawatt of electricity per year which can reduce a huge amount of CO2 emission annually. Therefore, global environmental issues are the main concern for researchers that is expected to continue expansion in the future. The traditional concept of converting wind energy to generate electricity is based on the Horizontal axes wind turbine (HAWT) and vertical axes wind turbine (VAWT). However, VAWT is not economically attractive as HAWT, though they offer energy solution for the remote area [4] . VAWT shows advantage compares to HAWT since these kinds of mechanics do not suffer from the frequent wind direction change and are suitable for structural and aesthetical reasons. Moreover, VAWT shows improved power in turbulent flows which is typical in built environment [5] . Development of micro-windmill, as an alternate source of energy, is increasing rapidly, to be utilized in the place where is close to the residential area or the rooftops. Safety is an important fact to operate wind turbine near the residential area. However, the wind turbine provides clean renewable energy but it has also some complications. Solving noise annoyance generated by the wind turbine is one of the important technical issues for the development of wind turbine used in the place where is close to the residential arena [6] . Also, mitigate the bird and bat mortalities caused by turbines is an area of research to be improved [7] [8] . Moreover, to utilize the hill effect in the residential arena, researchers are now focusing on the development and utilization of rooftop wind turbine [5] .
From a scope of diversity of wind turbines, the flapping wing wind turbines are a relatively new challenge for the researcher to consider an innovative development in order to preserve the natural environment or apply it to an urban area, so it gives an exciting proposition for the wind turbine as it provides the predictable amount of energy. In comparison with the traditional rotating wind turbine, we are focusing on a new concept regarding energy extraction by adopting a flapping mechanism. In nature, flapping wings are common for insects, birds, and other creatures. Their wing aerodynamics has been investigated by many researchers [9] [10] [11] . Development of flapping wing aerodynamics field has been inspired by flying animals such as bird’s and efficient swimmer like fishes. More recently researchers are focusing in this field due to the possible application of flapping wing for micro air vehicle (MAV) [12] . The working principle of a flapping wing is as similar as airplane wing and has a wide prospect for future applications in micro air vehicles (MAVs), nano air vehicles (NAVs) [11] [12] [13] . The characteristics of flapping wing aerodynamics depend on wing geometry, wing structural properties, flow condition and the kinematics of wing motion. As it’s a complicated task to understand flapping wing aerodynamics due to the leading-edge vortex, span wise flow and delayed stall phenomena, many researchers demonstrate “trial and error” approaches for flapping wing MAV [12] . These analyses on the flapping wing suggested that its mechanism has a universal advantage for low cost and sustainable energy resource in natural ecology.
On the other hand, to install wind turbine near residential area or rooftop, it is always an important issue to ensure structural stability, noise annoyance and slow rotating speed in terms of safety consideration. Slow flapping type VAWT is an innovative idea to resolve such unwanted problem as it can provide the predictable amount of energy. Considering all these facts, we proposed such a slow flapping type wind turbine. The flapping blade motion is controlled by various geometrical parameters for a given wind velocity and produced unsteady lift and drag forces by the wing and therefore works effectively for generating rotational torque. In our present research, we optimize the turbine design to create a suitable trajectory for flapping motion by the wing blade. To optimize the design, we emphasize on a combination of all parameters like link length, deltoid angle, mounting angle, the amount of generated torque and working ability of turbine. In flapping motion, the aerofoil’s angle of attack continuously changes which resulting in the change of circulation around the aerofoil [11] . The dynamic stall is one of the key parameters that debilitates the turbine efficiencies. A stall occurs due to the flow separation when turbine blade changes its position with large attack angle, once that happened the blade lift force is affected and drops significantly with overall energy extraction efficiency. To ride off this aerodynamic behaviour of aerofoil we consider small attack angle amplitude in our present flapping wind turbine design. In this paper, a numerical investigation carried out with the main objective is to design and develop a lift dominating flapping turbine fabricated with Chebyshev-dyad link mechanism to extract wind energy. Present turbine design considered as an alternative solution namely lift based (LB-type) relative to our previous turbine design, which was designed as lift and drag based (LDB-type) [14] . Moreover, implementation of a slower flapping wind turbine for practical use has been demonstrated focusing on usage near housing area or on rooftops due to less noise annoyance with a reasonable amount of power extraction. As far as the authors aware of, applying flapping wing concept for extracting wind energy is generally a new field to develop and no substantial research has been conducted yet.
2. Mechanism of Flapping Wind Turbine
The flapping wind turbine is a noble type of turbine where the blades are made of movable flaps. In this report, we consider a relatively new idea for wind energy extraction by adopting flapping mechanism where the blade flaps are controlled by various geometrical parameters for a certain wind speed. In our proposed flapping wind turbine with Chebyshev-dyad link mechanism by which the symmetric wing, NACA0012 can transfer the wind energy to mechanical rotation through a unique motion. As shown in Figure 1, the wing blade is connected to the rotor by Chebyshev-dyad linkage and the wind force is converted to rotating motion via this link mechanism. Therefore, linkage mechanism plays an important role in the mechanical arena to drive the generated forces as well as to transfer the forces in different output motions [15] [16] . To confirm stability in performance, applicability with high operation speed and high load bearing capabilities, it is important to confirm the suitable combination of these linkage geometrical parameters [17] [18] . The link length ratio, L1:L2:L3:L4; the blade mounting angle, ; and the deltoid angle,
; and the deltoid angle,  are the important controlled parameters for the movement of the flapping wind turbine. In general, Chebyshev-dyad link mechanism has the advantage of transforming mechanical forces by a symmetric curve to another symmetric one. For example, using Chebyshev- dyad linkage a symmetric 4-bar coupler curve can easily convert as a circular path [19] . A unique “figure eight” trajectory considered as an input curve of Chebyshev- dyad and the output curve identifies as a circular curve in our present system. Figure 2 shows the schematic view of flapping wind turbine. For present system, a set of two linkages supports a single blade, NACA0012 mounted normal to the flow direction.
are the important controlled parameters for the movement of the flapping wind turbine. In general, Chebyshev-dyad link mechanism has the advantage of transforming mechanical forces by a symmetric curve to another symmetric one. For example, using Chebyshev- dyad linkage a symmetric 4-bar coupler curve can easily convert as a circular path [19] . A unique “figure eight” trajectory considered as an input curve of Chebyshev- dyad and the output curve identifies as a circular curve in our present system. Figure 2 shows the schematic view of flapping wind turbine. For present system, a set of two linkages supports a single blade, NACA0012 mounted normal to the flow direction.
![]()
Figure 1. Flapping wind turbine’s trajectories and geometry.
![]()
Figure 2. Flapping wind turbine schematics.
In the flapping design, the blade fixed on a predetermined point with the constant mounting angle and the wing blade moves through the unique trajectory, i.e. the wing fixed at point K in Figure 1 moves through the figure eight trajectory in the cycle. The point-A draws a rotational motion and point-B draws a rocking motion which is associated with the movement of the wing blade. Therefore, with the movement of the wing blade along the trajectory, the angle of attack changes continuously. The attack angle variation at different wing positions for a static wind speed directly affected the aerodynamic forces generated by the wing blade. Once the flapping turbine is in motion, the generated aerodynamic forces by the wing blade convert as rotor rotational motion through the Chebyshev-dyad linkage. Due to the periodic movement of the wind turbine, even though the flow is uniform the relative velocity of the wing blade and flow direction varies in each cycle. A rapid change of attack angle beyond the stall condition and flow separation occurs due to the large angle of attack. Though a large angle of attack inevitably appears in a certain region, in this circumstance the wing enters in a stall but maintains a large lift and drag coefficients, by designing a suitable trajectory for the turbine we can get an effective driving force [14] . The stall is an unsteady phenomenon and difficult to approximate the turbine performance accurately under the stall condition. Therefore, in our present turbine design, we overlook the stall phenomenon owing to large attack angle in motion by focusing on a slow flapping wind turbine operated within a small attack angle amplitude, i.e. lift based flapping wind turbine. The wind direction angle,  is considered 90˚ and the rotor rotation is an anti-clockwise direction for the present system. Aerofoil’s chord length and wing span are select as 0.2 m and 0.3 m respectively for present study (Figure 3).
is considered 90˚ and the rotor rotation is an anti-clockwise direction for the present system. Aerofoil’s chord length and wing span are select as 0.2 m and 0.3 m respectively for present study (Figure 3).
3. Mechanical Analysis
In the present flapping wind turbine, a single wing blade of aerofoil profile NACA0012 converts the kinetic energy to aerodynamic forces depending on the angle of attack. Also, compared to traditional rotating wind turbine wing, flapping wing induces a distinct aerodynamic flow mechanism by varying position and orientation [20] and due to the cyclic movement of the wind turbine, even
![]()
Figure 3. The inner product between resultant force and the blade trajectories.
though the flow is uniform, the relative velocity of the wind blade and flow direction varies during a cycle. Therefore, the aerodynamic force coefficient depends directly on the angle of attack with the relative flow velocity. The Reynolds number considered for the flow velocity from 5 m/s to 12 m/s varies within a range of 6.6 × 104 to 2.0 × 105. The Reynolds number in the present system for the wind velocity of 10 m/s is close to the value of 1.6 × 105 considered in the literature [21] .
According to the geometrical relation shown in Figure 1, putting O as origin, the corresponding coordinates of points ,
,  ,
,  , and Point
, and Point 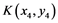 were given in similar way as described in the previous paper [14] .
were given in similar way as described in the previous paper [14] .
The angle of attack of the wing is determined using the following relation with the mounting angle, 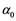 and the wind angle,
and the wind angle,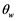 :
:
 (1)
(1)
In the present system, the resultant force act in the rotational direction and work as the main driving force through an eight-shaped trajectory. Through the link mechanism, air flow converts to a rotatory motion which rotates a generator connected by a vertical shaft for power generation. Lift and drag forces are calculated as:
 (2)
(2)
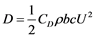 (3)
(3)
Considering synthesis of a link mechanism for numerical analysis with the equilibrium of forces and moment for each linkage OA, BC and deltoid ABK as similar our previous flapping wind turbine [14] to evaluate the torque generated by the rotatory motion [17] [18] . The generated torque was determined by solving all equations of equilibrium with the lift and drag force as described in the next equation.
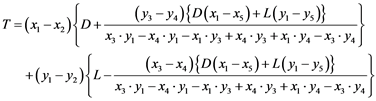 (4)
(4)
The rotational angular velocity of the rotor was calculated by solving the following equation of motion for a rigid body by using an explicit fourth order Runge-Kutta method.
 (5)
(5)
where I represent the inertia moment for the rotating disk with radius (r) which was assumed by summing up predicted masses (M) as the generator and shaft, etc. to make it a more practical application for different load conditions.
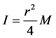 (6)
(6)
When the turbine is in motion, the relative velocity is calculated with wing velocity as follows:
![]() (7)
(7)
The rotor speed is variable in our present system, therefore the wing velocity calculated as indicated in the next equations.
![]() (8)
(8)
![]() (9)
(9)
The relative inlet angle is calculated as follows
![]() (10)
(10)
Here, the number i represents the calculational nodal number.
There are several key parameters related to wind turbine which can quantify the turbine performance under certain situation. In general, wind flow can harness mechanical energy through rotating a wind turbine by blades. The mechanical energy can convert to electric energy through a generator. The reference wind power for incoming wind can be evaluated as
![]() (11)
(11)
Here, A is the cross section that the wing traverses in its motion. The output power for wind turbine is defined as
![]() (12)
(12)
The power coefficient, ![]() is determined as Equation (13) with a dimensionless form, for which the theoretical maximum value is known as Betz’s coefficient as 0.593.
is determined as Equation (13) with a dimensionless form, for which the theoretical maximum value is known as Betz’s coefficient as 0.593.
![]() (13)
(13)
4. Optimization Procedures
In the present system, there exists many parameters, it is hard to use single formulation procedure for all engineering design problem due to the variation of objectives and constraints in the design problem [22] [23] [24] . In optimization approach, we have to focus on the primary objective of the optimization. Here, we need to address the variables influencing the optimization problem. Since some sort of parameterization is required, we at first seek a set of input parameters which can fully characterize the problem. The parameters are considered as an important factor in design, if the variation of the parameter may affect significantly the performance measure of the problem. Moreover, it must be kept in mind that the complexity of an optimization increasing exponentially with the number of parameters, thus the number of variables needs to be minimum as much as possible [25] . In the mechanical design with an optimization process, designers always consider certain objectives such as strength, weight, output measure, lifetime etc. However, design optimization for a complete mechanical assembly leads to a complicated objective function with many design variables. So, it is always a good practice to apply optimization techniques for individual components or intermediate design than a complete design [26] . In the practical design problems, the number of design parameters is very large in general and their influences on the objectives function may be complicated owing to nonlinear characteristics. However, the objective functions have many local extrema, but, designers always interested in global extremum under certain region.
Returning to the present optimization, the design of flapping wind turbine directly depends on several parameters such as internal coupler angle, mounting angle, link length properties, attack angle amplitudes and direction of the wind. Each parameter is interlinked with others by which means the variation of one parameter will directly affect others. Therefore, discussion about these parameters together shows a significant variant in the overall performance and trajectory of the wind turbine. It is important to optimize all design parameters for smooth flapping motion with better performance moving with small attack angle amplitude in turbine motion. To achieve our goal from present investigation, the optimization has been performed by maintaining iterative procedure, details in Figure 4. For fixing the optimized design parameters, we emphasize on maintaining mechanical balance, unique trajectory, small attack angle amplitude, turbine
![]()
Figure 4. Parameters optimization flowchart for optimal design procedure.
overall working ability, the amount of generated torque, and slow flapping motion. To evaluate the designed turbine performance, the simulation has been conducted using our developed MATLAB code.
5. Static Simulation
A change in deltoid angle (
![]()
Figure 5. Variation of trajectory by the wing blade for different deltoid angle.
![]()
Figure 7. Variation of angle of attack in one complete rotation of the wing for different deltoid angle.
![]()
Figure 8. Average cosine value obtained for one complete rotation with different deltoid angle, ψ.
comparing with other position and maintain small attack angle amplitude for the wing in motion.
Mounting angle is another important parameter for the flapping wind turbine design. Though it has no influence of the trajectory shape still plays an important role for the overall performance of the wind turbine. To operate the flapping wind turbine under small attack angles, mounting angle considered as an important parameter in the present system. As mounting angle directly changes the bias for the angle of attack, the different mounting angle will provide a different angle of attack amplitude during the turbine rotation. Also, the varying angle of attack amplitude has the direct influence on aerodynamic force generation. Figure 9 shows the average tangential force generated during one rotation for different mounting angle position at a fixed wind speed 5 m/s. Figure 10 shows the variation of attack angle for one period with different mounting angles.
![]()
Figure 9. Average tangential force for varying mounting angle at a wind speed of 5 m/s.
![]()
Figure 10. Variation of angle of attack by the wing blade for different mounting angle.
Therefore, we approval the optimum mounting angle as 90˚ for the present design, so it provides the maximum tangential force with suitable attack angle amplitude in turbine motion.
Let’s estimate the linkage lengths in Chebyshev-dyad, which is important for the turbine design as the trajectory and turbine performances vary with small variation of link lengths. To obtain better performance from the flapping wind turbine with maintaining the mechanical balance of the linkage, it is important to consider the proper position as well as the optimum length of each linkage. Initially, we consider the link length L1 = 0.05 m as a pre-assumed parameter and other suitable link lengths should be determined for the optimum performance of the system. Link length, L2 and Link length, L4 are same to allow the Chebyshev criteria. From the calculated outcomes, we notice that when the difference between L2 and L3 is large, in that time the linkage balance of the system breakdown and outcomes become favorable for the design when the difference was tiny between L2 and L3. To maintain small attack angle amplitude in our flapping motion the position of point C shift wider from the origin point O. Consider the example of varying link length L2 with other fixed parameters: link lengths L1 equals to 0.05 m, L3 equals to 0.3 m, deltoid angle equals to 60˚ and the wind velocity 5 m/s; this gives the variation of torque curves shown in Figure 11 with average torque values. Figure 12 shows the different trajectories generated by the wing blade for different link length, L2. A small variation of the link length L2 makes the torque curve variation with the trajectory and the trajectory variation influences the angle of attack curves as well as the overall performance of the wind turbine. Figure 13 shows a summary of the average torque values simulated for different link lengths L2, L3 and L4 with the individual linear change to obtain maximum torque. In each case, the variation of one link length with the other link length fixed as 0.3 m. Also, Figure 14 shows a relation of the average cosine value for the link length L2, L3 and L4 with linear change for the same criteria. Therefore, small differences in link length L2 and L3 considered as a favorable neighboring region for the design and same values of these two-link lengths provide enhanced results in terms of trajectory shape, average torque value, average cosine value and small attack angle amplitude for one complete rotation.
The preferable values obtained by static analysis for the present wind turbine are the link length ratio (L1:L2:L3:L4) as 0.05:0.3:0.3:0.3; the deltoid angle, ψ is 60˚;
![]()
Figure 13. Average torque value curve based on varying link lengths, L2, L3 and L4.
and the mounting angle, α0 is 90˚. Under these values, Figure 15 shows the relationship of various torque developed with different wind velocities. The small negative torque was found due to the wing blade changes its direction of motion, whereas inertia governs the continuation of motion for dynamic cases. Maximum torque for one complete rotation achieved around 270˚ of the rotor rotation angle. Static torque curve shows similar in trend with the increasing of wind velocities and the amount of average torque increases with wind velocity which is obvious in general.
![]()
Figure 14. Average cosine value curve based on varying link lengths, L2, L3 and L4.
![]()
Figure 15. Static torque development for one rotation with different wind speeds.
6. Dynamic Simulation
To estimate more practical approximations for the present wind turbine, dynamic analysis has been conducted with the optimum parameters based on the static analysis. In this simulation, the motion of equation was solved with relative velocity details were discussed in Section 3. Figure 16 shows the generated torque obtained from the dynamic motion of the wind turbine at three different wind speeds 5 m/s, 7 m/s, and 9 m/s. The dynamic simulation started from θ1 = 0 and from the rest state. The increment angle was taken as 0.01 degrees. Figure 16 shows the dynamic torque during 5 seconds after the motion start. In the dynamic simulation, the turbine is accelerated in some duration and approaches to equilibrium rotation speed.
As the motion starting condition considered from rest state means no load condition was assumed and with the rotor acceleration load condition taken into consideration for the simulation model. Figure 17 shows the development of angular velocity for V0 = 5, 7, and 9 m/s. We can notice from the figure that each curve shows a large gradient and fluctuation just after the beginning, in this
![]()
Figure 16. Transient torque at different wind velocities up to 5 s.
![]()
Figure 17. Development of angular velocities for different wind speeds with respect to time.
motion, the generated torque is spent for the generation of motion. To achieve quasi-steady motion become faster with the increasing of wind velocities. In Figure 17, we assumed torque distributed function Φ = Φ(90%_10%), i.e., the turbine load as ninety percent of the generated torque under three different wind velocities, which used for the counterbalance of load generated by the generator and rest of the torque used for the motion continuation. Figure 18 shows the developed angular velocity at wind speed 5 m/s under three different load conditions.
7. Comparison of Static and Dynamic Torques
The comparison of generated torque curve between static and dynamic simulation is demonstrated in Figure 19 for one cycle under three different wind velocities of 5, 7, and 9 m/s respectively. Since the dynamic torque varies after the turbine starts, the dynamic torque data was sampled after the angular velocities reached in the quasi-steady rotation speed. For both cases, the curves show similar tendency as we expected, however, the dynamic torque curve shows a little
![]()
Figure 18. Development of angular velocities with respect to time under different torque distribution at wind speed 5 m/s.
lower in the first half cycle but little bit upper in the second half relative to the static torque curve. Of course, the difference is attributed to the relative velocity owe to the blade rotation.
8. Power Coefficient
The dynamic analysis gives a perception of the new flapping wind turbine performance. As the generated torque varies with rotation angle, the generated power shows the fluctuation, so the power coefficient curves also vary depending on the rotation angle. Figure 20(a) represent the power developed by the wind turbines up to first 10 s starting from rest state and Figure 20(b) represent the power developed by the wind turbines for 5 s when the turbine performance reached in quasi-steady rotation speed at wind speed 7 m/s with torque distributed function Φ = Φ(90%_10%). Similarly, Figure 21(a) represent the power developed by the wind turbines for first 10 s and Figure 21(b) represent the power developed by the wind turbines for 5 s when the turbine performance reached in quasi-steady state at wind speed 7 m/s with torque distribution function Φ = Φ(80%_20%). As more torque is used for the motion continuation, the angular velocity of the wind turbine increases with time which has a direct influence on turbine performances. Figure 22 represents the average developed power by the wind turbine with a wide range of variation in wind speed.
Figure 23(a) represent the power coefficient curve developed by the wind turbines up to first 10 s starting from rest state and Figure 23(b) represent the power developed by the wind turbines for 5 s when the turbine performance reached in quasi-steady state at wind speed 7 m/s with torque distributed function Φ = Φ(90%_10%). Similarly, Figure 24(a) represent the power coefficient developed by the wind turbines up to first 10s starting from rest state and Figure 24(b) represent the power developed by the wind turbines for 5 s when the turbine performance reached in quasi-steady state at wind speed 7 m/s with torque distribution function Φ = Φ(80%_20%). As more percentage of developed torque
![]()
![]()
![]()
Figure 19. Comparison of static and dynamic torques for three different wind velocities 5, 7, and 9 m/s respectively.
are used for the motion continuation, the angular velocity of the wind turbine increases with time which has a direct influence on turbine performances. Figure 25 represents the average developed power coefficient by the wind turbine for a wide range of wind speed variation. The vertical line in the Figure 25 shows the oscillation of power coefficients when turbine is in motion under different wind speed.
![]() (a) Φ = Φ(90%_10%)
(a) Φ = Φ(90%_10%) ![]() (b) Φ = Φ(90%_10%)
(b) Φ = Φ(90%_10%)
Figure 20. Power curve with time at wind speed 7 m/s.
![]() (a) Φ = Φ(80%_20%)
(a) Φ = Φ(80%_20%) ![]() (b) Φ = Φ(80%_20%)
(b) Φ = Φ(80%_20%)
Figure 21. Power curve with time at wind speed 7 m/s.
![]() (a) Φ = Φ(90%_10%)
(a) Φ = Φ(90%_10%) ![]() (b) Φ = Φ(80%_20%)
(b) Φ = Φ(80%_20%)
Figure 22. Power curve for different wind velocities.
![]() (a) Φ = Φ(90%_10%)
(a) Φ = Φ(90%_10%) ![]() (b) Φ = Φ(80%_20%)
(b) Φ = Φ(80%_20%)
Figure 23. Power coefficient curve with time at wind speed 7 m/s.
![]() (a) Φ = Φ(90%_10%)
(a) Φ = Φ(90%_10%) ![]() (b) Φ = Φ(80%_20%)
(b) Φ = Φ(80%_20%)
Figure 24. Power coefficient curve with time at wind speed 7 m/s.
![]() (a) Φ = Φ(90%_10%)
(a) Φ = Φ(90%_10%) ![]() (b) Φ = Φ(80%_20%)
(b) Φ = Φ(80%_20%)
Figure 25. Power coefficient curve for different wind velocities.
9. Comparison with LB-Type and LDB-Type
The characteristic performances obtained for the static case at wind velocity 5 m/s of the lift based flapping wind turbine has been compared with our previously designed flapping wind turbine [14] . The attack angle variation at different wing positions for a fixed wind speed directly affected the aerodynamic forces generated by the wing; Figure 26(a) represents the angle of attack variation by the wing blade for one complete rotation. In Figure 27(a) and Figure 27(b) shows the lift and drag forces generated from the wind by the flapping wing blade for one complete rotation. In Figure 27(a), the lift curve in the present turbine is smoother compared to previous one and generated a negligible amount of drag force whereas the previous design shows a high gradient in the first half of the wing blade rotation as shown in Figure 27(b). The developed
![]() (a)
(a) ![]() (b)
(b)
Figure 26. (a) Comparison of angle of attack variation for one complete rotation; (b) Comparison of torque curves for one complete rotation at wind speed 5 m/s.
![]() (a)
(a) ![]() (b)
(b)
Figure 27. (a) Comparison of lift force developed for one complete rotation at wind speed 5 m/s; (b) Comparison of drag force developed for one complete rotation at wind speed 5 m/s.
static torque curved for one complete rotation has been compared in Figure 26(b), the average torque value is 0. 030 N・m at 5 m/s wind speed for our new lift based flapping wind turbine which is tiny low compared to our previous lift and drag based flapping turbine at similar wind speed. In the new design, the torque curve for one rotation of the wind turbine is quite smooth compared to previous design which is considered as one of advantage in our new turbine’s performance.
The dynamic performance obtained from lift based flapping wind turbine also compared with our previously designed lift and drag based flapping wind turbine. We consider two different cases: 1) Φ = Φ(90%_10%), i.e., 90% of generated torque developed in dynamic motion consumed to counterbalance the load generated by the generator and remaining torque used for the motion continuation; and 2) Φ = Φ(80%_20%), i.e., 80% of generated torque developed in dynamic motion consumed to counterbalance the load generated by the generator and remaining torque used for the motion continuation. Figure 28(a) and Figure 28(b) represents the angular velocity comparison at a wind speed of 5 m/s. Figure 29 represents the power curve comparison for present turbine design with previously designed wind turbine at a wide range of wind velocity. In each wind speed, we found that LB-type flapping wind turbine provides more average power compared to previous designed flapping wind turbine for same torque distribution in dynamic motion. Similarly, Figure 30 represents the power coefficient curves comparison for LB-type design and LDB-type design at a wide range of wind velocity. We consider both cases as same as for power curves. Also for variation in wind speed, we notice that LB-type flapping wind turbine provide more average power coefficient compare to previously designed flapping wind turbine for same torque distribution in dynamic motion. In conclusion, the new lift based flapping wind turbine can be considered as a good alternate of our previously designed lift and drag based flapping wind turbine.
![]() (a) Φ = Φ(90%_10%)
(a) Φ = Φ(90%_10%) ![]() (b) Φ = Φ(80%_20%)
(b) Φ = Φ(80%_20%)
Figure 28. Comparison of angular velocity with time at wind speed 10 m/s.
![]() (a) Φ = Φ(90%_10%)
(a) Φ = Φ(90%_10%) ![]() (b) Φ = Φ(80%_20%)
(b) Φ = Φ(80%_20%)
Figure 29. Comparison of power developed by turbine for different wind velocities.
![]() (a) Φ = Φ(90%_10%)
(a) Φ = Φ(90%_10%) ![]() (b) Φ = Φ(80%_20%)
(b) Φ = Φ(80%_20%)
Figure 30. Comparison of power coefficient for different wind velocities.
10. Conclusions
A flapping type wind turbine operated with a small attack angle amplitude has been demonstrated in this report. The proposed wind turbine rotates along with “figure eight” trajectory, which was fabricated by Chebyshev-dyad linkage. In this report, we designed “lift-based” (LB-type) flapping turbine, comparing with the previous “lift-drag based type” (LDB-type).
The turbine characteristics for the different combination of geometrical parameters have been investigated by the correlation of the inner product between resultant force and the slope of the trajectory. The feasibility of the proposed turbine is confirmed by optimizing variable parameters to attain the optimum performance in a certain region. The optimal parameters for the design are considered as link length ratio, L1:L2:L3:L4 was 0.05:0.30:0.30:0.30, deltoid angle ψ = 60˚, mounting angle α0 = 90˚ respectively. The parameters are determined to generate a high amount of torque with a smooth flapping motion by the wing blade moving through a unique figure-eight trajectory and maintain small attack angle amplitude. Both static and dynamic numerical analyses were conducted to estimate the characteristics behavior of the wind turbine for different wind velocities. The developed torque obtained from the static analysis was compared with the dynamic torque for one complete rotation of the rotor and makes a good agreement indeed.
The flapping wind turbine utilizes the generated force by the single wing blade effectively to convert a decent amount of mechanical power in a slow speed. Moreover, the amount of generated average power, as well as average power coefficient for flapping wind turbine operated within small attack angle shows the large gradient in comparison with LDB-type wind turbine. In addition, the power production of LB-type can increase by extending the length and the width of the blade. Furthermore, the shape and size of the flapping wind turbine are possible to increase for more power generation depending on the region of turbine installation without affecting the objectives of the wind turbine.