1. Introduction
Ever since their discovery in 2008 by Kamihara et al. [1] , the iron-based superconductors (FeSCs) characterized by multiple gaps (Δs) and high-Tcs have been avidly investigated both experimentally and theoretically. This is evidenced by at least ten review articles in a relatively short period, as has been noted in another, more recent, review by Bang and Stewart [2] . While the issue of the pairing mechanism in FeSCs remains an open question, the conventional theoretical approaches proposed to deal with them have been broadly categorized in [2] as based on the Random Phase Approximation, the Functional Renormalization Group Technique, and the Local Pairing Approach. A common feature of these is their adaptations of the multi-band concept, which was pioneered by Suhl et al. [3] . We propose in this note to show that many properties of FeSCs are also explicable quantitatively via another approach which is based on a generalization of the one-band Bardeen-Cooper-Schrieffer equations (GBCSEs) in the mean- field approximation.
Since such a proposal may prima facie seem as bizarre, there seems a need at the outset to make it physically plausible that the approach based on GBCSEs may, at least, play a valuable role in supplementing the conventional multi-band approach. This need is addressed in Section 2, where (a) the genesis of employing the multi-band approach for high-Tc SCs is outlined and (b) the physical content of GBCSEs is summarized. For the sake of concreteness, we apply GBCSEs here to the most widely investigated FeSC, i.e., Ba0.6K0.4Fe2As2 (BaAs hereafter). Listed in Section 3 therefore are its main properties, which are based on various experiments and the conventional theoretical approaches. The study of BaAs via GBCSEs incorporating chemical potential μ (equivalently Fermi energy EF, as will be discussed below) is taken up in Section 4 and is shown to lead to the important result that EF characterizing it is ~14 meV. In Section 5 we show how this result enables us to shed light on the properties of the SC that were noted in Section 3, Sections 6 and 7 are devoted, respectively, to a Discussion and Conclusions of our approach.
2. Multi-Band Models and GBCEs
Because SCs characterized by multiple gaps are most commonly addressed by invoking multi-band models, with an apology to the cognoscenti, we first trace below the backdrop of these models. This is followed up by an account of the physical considerations that led to GBCSEs.
2.1. The Multi-Band Models
The conceptual basis for multi-band models in general is provided by Suhl et al. [3] who dealt with the superconductivity of transition elements. A peculiar feature of these elements is the filling up of the 4s orbital prior to the 3d orbital, which implies that the valence electrons in these elements are divided between two bands. Therefore, the s-electrons can be scattered not only within their own band, but also to the d-band. Because the latter band has more vacant levels than the former, it makes a large contribution to the total density of states N(0). Two gaps and, in general, two Tcs arise in this approach because the BCS interaction parameter λ ≡ [N(0)V] is now determined via a quadratic equation involving interaction energies V between pairs of electrons in the two bands individually and those that are scattered from one band to the other. It is to be noted that in this model the equation employed to determine Tc− for each value of λ ? is identical with the equation that determines this parameter in the original, one-band BCS equation. Since the latter equation has been shown to follow from a Bethe-Salpeter equation (BSE) in the scenario of one-phonon exchanges between Cooper pairs (CPs) [4] [5] , and since this approach must satisfy the Bogoliubov constraint, i.e. λ ≤ 0.5, it follows that it cannot, per se, account for such high-Tcs as have been observed. This of course is the reason why numerous attempts have been made to integrate the multi-band concept with the well-known Migdal-Eliashberg-McMillan approach [6] . The latter approach allows λ to be greater than unity because it is based on an integral equation the successive terms in which are smaller by a factor of (me/M), rather than λ; here me is the mass of an electron and M that of an ion. Since λ can now be greater than unity, it has been implied that the occurrence of high-Tcs is explicable via this approach. Note however that this is a surmise made by remaining in the conceptual mould where formation of CPs is brought about via one-phonon exchange mechanism (1PEM), ignoring the possibility that in a composite SC electrons may also be bound via simultaneous phonon exchanges with more than one species of ions―each of which is distinguished by its own Debye temperature and interaction parameter.
2.2. GBCSEs: Physical Basis
Superconductivity in any material has to-date been understood solely as arising due to the formation of CPs. In elemental SCs, pairing is brought about via 1PEM due to a net attraction between pairs of electrons because of the ion-lattice and the Coulomb repulsion.
No single-component SC has yet been found with a Tc exceeding that of Nb, i.e., 9.25 K (∆ ≈ 1.55 meV). In the light of this observation, a general feature of SCs characterized by high-Tcs and multiple gaps is striking: all of them are multi-component materials. This naturally suggests that CPs in these may be bound via simultaneous exchanges of phonons with more than one species of ions ? in addition to those that are bound via 1PEM due to each ion species separately. It has been shown that the BCS equation for the Tc of an elemental SC follows by summing an infinite number of ladder diagrams in the 1PEM scenario [4] [5] . The first diagram in this series has one step or rung, the second two rungs, and so on. If the number of rungs between any two space-time points in each of these diagrams is doubled, then we have the 2-phonon exchange mechanism (2PEM) in operation. Similarly, CPs may also be bound via the 3-phonon exchange mechanism (3PEM) if the SC contains three species of ions that can potentially cause formation of CPs. It then follows that in a multi-component SC, CPs may exist with different values of the binding energy (2|W|). Since the binding energy of CPs in the 3PEM scenario must be greater than in the 2PEM scenario, which in turn must be greater than in the 1PEM scenario, and since |W| = ∆ [5] , we are naturally led to an explanation of why multi-component SCs are characterized by multiple gaps. Equations for the |W|s and Tcs of composite SCs have been derived by invoking multiple-phonon exchange mechanism for pairing―which simply means that the one-phonon propagator in the BSE which leads to the BCS expression for the Tc of an elemental SC is replaced by a “superpropagator”. Since the equations so obtained manifestly generalize the corresponding BCS equations for an elemental SC, they were christened as GBCSEs.
3. Properties of Superconducting BaAs
In the following Sections, we shall show how GBCSEs enable one to correlate several properties of BaAs and shed light on others. These properties are listed below; they include not only those that are determined via different experiments, viz., the angle-resolved photoemission spectroscopy (ARPES), the scanning tunnelling microscopy, and specific heat and penetration-depth measurements, but also those determined via theoretical investigations based on multi-band models and a study of the crossover from a BCS state to a Bose-Einstein Condensed state (crossover hereafter).
Properties of BaAs addressed in this note:
(i) Superconductivity in this SC is due to the 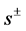 - wave state, which signifies that the gaps below a Fermi surface and above it, Δh and Δe, respectively, have opposite signs [2] ;
- wave state, which signifies that the gaps below a Fermi surface and above it, Δh and Δe, respectively, have opposite signs [2] ;
(ii) In general, 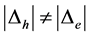 [2] ;
[2] ;
(iii) Tc = 37 K [7] ;
(iv) Maximum value of Tc for several FeSCs [8] [9] :
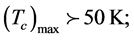
(v) Δ1, Δ2 = 6, 12 meV [10] ;
(vi) Near-zero values of Δ: As reported in several papers, e.g., [11] , Δ for the SC being considered can fall to zero along lines of the Fermi surface
(vii) Some of the other reported values of Δ (in meV): 2.5, 9.0 [12] , 3.3, 7.6 [7] , 3.6, 8.5, 9.2 [13] ; 4, 7 12, 9.5 [14] ,
(viii) Crossover: It has been asserted that BaAs lies nearly in the middle of crossover regime [15] with Δ/EF ratios as:
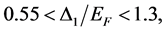

The last equation is obtained via a two-band model for which the Fermi energies are defined as  with ε1 = 0 and tuneable ε2 ≥ 0;
with ε1 = 0 and tuneable ε2 ≥ 0;
(ix) The critical current density j0: It has been reported as exceeding 0.1 MA cm−2 [16] at T = 4.2 K and H = 0 T (H being the external magnetic field) and as 1.1 × 107 Acm−2 [17] at 2 K and 0 T. Based on these experimental values we estimate j0 for BaAs as ≈ 2.5 × 107 Acm−2 at T = H = 0;
(x) Another characteristic ratio, see, e.g., [9] :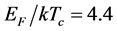 ;
;
(xi) The band effective mass m* and the free electron mass me: In a study of BaAs based on ARPES and a four-band model, Ding et al. [18] have reported that in one of the bands, 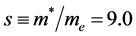 (other values are lower), and have estimated
(other values are lower), and have estimated
(xii) The coherence length ξ as 9 - 14 Å; and finally,
(xiii) Dome-like structure: Tc of the SC plotted against a “tuning variable” has a dome-like structure [9] .
4. Study of BaAs via GBCSEs
4.1. Equation for |W| in the 1PEM Scenario and the BCS Equation for Δ
Prior to undertaking the study of BaAs via the multi-phonon exchange mechanism, we recall that the equation for |W| at T = 0 in the 1PEM scenario (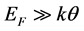 ) is [5] :
) is [5] :
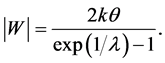
For the sake of comparison, we also recall the BCS equation for Δ:

which follows from an equation quadratic in Δ. Significantly, the equation for W has been derived by assuming that its sign changes in going from below the Fermi surface to above it, which is (a) akin to a similar change in the velocity of a quasi-particle, as discussed by Rickayzen [19] , and (b) also the case for all the equations employed below. Hence from the outset our approach is based on the 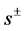 - wave feature noted as Property (i) above. It was shown in [20] via a detailed study of six elemental SCs that the above equation for |W| is a viable alternative to the equation for Δ.
- wave feature noted as Property (i) above. It was shown in [20] via a detailed study of six elemental SCs that the above equation for |W| is a viable alternative to the equation for Δ.
4.2. Debye Temperatures (θs) of the Constituents of BaAs
The first step in the application of GBCSEs to any composite SC is to identify the ion species that may cause pairing. For BaAs, we identify them as Ba, Fe and As. Given θBaAs = 274 K [21] and the masses of the ion-species, the next step is to fix θBa, θFe, and θAs, which must be different because the masses of the ions are different. One way of doing this is to assume that the modes of vibration in any layer of the SC simulate the modes of vibration of a double pendulum. For the layer containing Ba and K ions, for example, we are then led to two values for both θBa and θK? one corresponding to Ba as the upper bob of the double pendulum and K as the lower bob and the other by interchanging the positions of the bobs. We are similarly led to two values for both θFe and θAs. While all these values have been given in [22] , we adopt here the following set (this will be further discussed below):
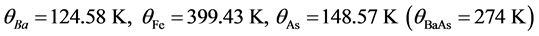 (1)
(1)
4.3. GBCSEs Sans μ
We first deal with the gaps and the Tc of BaAs via GBCSEs sans μ, which were obtained by assuming that EF (or μ) ? kθ. The results so obtained will be seen to provide a consistency check of the μ-incorporated GBCSEs in the next section.
The features of BaAs that we take as our starting point are
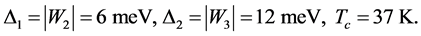 (2)
(2)
Since GBCSEs are based on the formation of CPs via multi-phonon exchange mechanisms, let us define W1, W2 and W3 as the T = 0 values of (half) the binding energies of pairs formed via 1PEM, 2PEM and 3PEM, respectively. We now identify W2 with the smaller and W3 with the larger of the two gaps in the set of Equations (2) and the value of Tc as the temperature at which W2 vanishes. While 2PEM can be caused by any combination of ions such as (Ba + As), (Fe + As), and (Ba + Fe), all of which were considered in [22] , for the limited purpose of checking the consistency of equations in the next section, we now adopt the last of these options. Then, for EF (or μ) ? kθBaAs we have the following set of equations [22] (Wi = |Wi|):
 (3)
(3)
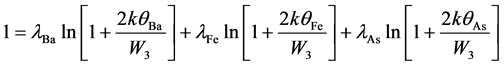 (4)
(4)
![]() (5)
(5)
Solutions of the above equations, with inputs from the sets of Equations (2) and (3), lead to {λBa = −0.0484, λFe = 0.4254, and λAs = 0.2084}. Since each value of λ must satisfy the Bogoliubov constraint (0 < λ ≤ 0.5), this set of solutions in unacceptable. This situation is addressed by a minor fine-tuning of the input variables as discussed in detail in [23] . In the present instance, it turns out that solely changing |W2| from 6 to 6.2 meV leads to the following acceptable set
![]() (6)
(6)
4.4. μ-Incorporated GBCSEs
Generalized versions of Equations (3)-(5) that do away with the constraint EF (or μ) ? kθ are [24] :
![]() (7)
(7)
![]() (8)
(8)
![]() (9)
(9)
where
![]() (10)
(10)
![]() (11)
(11)
![]() (12)
(12)
![]() (13)
(13)
![]() (14)
(14)
and
![]() (15)
(15)
In the above equations, the superscripts of ![]() and
and![]() , for example, denote that the expressions for them correspond to 2PEM and 3PEM scenarios, respectively. Further, among the Debye temperatures of the ion-species that contribute to each of Equations (7)-(9), the value chosen in the second term is the one that has the greatest value (i.e., θFe) because a lower value would curtail the region of pairing due to one or the other species of ions. For later reference, we note that the equation for Tc corresponding to the vanishing of W3 is obtained by replacing
, for example, denote that the expressions for them correspond to 2PEM and 3PEM scenarios, respectively. Further, among the Debye temperatures of the ion-species that contribute to each of Equations (7)-(9), the value chosen in the second term is the one that has the greatest value (i.e., θFe) because a lower value would curtail the region of pairing due to one or the other species of ions. For later reference, we note that the equation for Tc corresponding to the vanishing of W3 is obtained by replacing ![]() in Equation (9) by
in Equation (9) by![]() :
:
![]() (16)
(16)
For![]() , the solutions of Equations (7)-(9) must agree with those of Equations (9)-(11). This requirement is satisfied because on solving the former equations for
, the solutions of Equations (7)-(9) must agree with those of Equations (9)-(11). This requirement is satisfied because on solving the former equations for ![]() and inputs from the set of Equations (1) and (2) (with |W2| replaced by 6.2 meV) we are led precisely to the solutions given in Equations (6). We may therefore employ Equations (7)-(9) for any value of
and inputs from the set of Equations (1) and (2) (with |W2| replaced by 6.2 meV) we are led precisely to the solutions given in Equations (6). We may therefore employ Equations (7)-(9) for any value of![]() . The next step in our study is to solve these equations for different values of μ in an appropriate range.
. The next step in our study is to solve these equations for different values of μ in an appropriate range.
4.5. Solutions of the μ-Incorporated GBCSEs
For some select values of μ in the range ![]() and inputs from the sets of Equations (1) and (2), we have given in Table 1 the values of λBa, λFe and λAs obtained via solutions of Equations (7)-(9). In accord with a basic tenet of the BCS theory, we have assumed that these λs have the same values at T = 0 and T = Tc. We also assume μ to be temperature-independent, and use it interchangeably with EF because it has been found these differ insignificantly for the wide variety of six SCs dealt with in [24] . It is then seen that for the lowest value of μ in the range under consideration, i.e., μ = 1.5 kθBaAs = 35.4 meV, ∆1/μ = 0.175 and ∆2/μ = 0.349. Guided by the values of these parameters obtained via a
and inputs from the sets of Equations (1) and (2), we have given in Table 1 the values of λBa, λFe and λAs obtained via solutions of Equations (7)-(9). In accord with a basic tenet of the BCS theory, we have assumed that these λs have the same values at T = 0 and T = Tc. We also assume μ to be temperature-independent, and use it interchangeably with EF because it has been found these differ insignificantly for the wide variety of six SCs dealt with in [24] . It is then seen that for the lowest value of μ in the range under consideration, i.e., μ = 1.5 kθBaAs = 35.4 meV, ∆1/μ = 0.175 and ∆2/μ = 0.349. Guided by the values of these parameters obtained via a
![]()
Table 1. Values of λBa, λFe, and λAs calculated via Equations (7)-(9) with inputs from Equations ((1) and (2)) and different assumed values of μ/kθBaAs. y is obtained by solving Equation (20), and j0 via Equation (18) with additional inputs from Equation (27).
crossover study [15] ―see Property (viii) in Section 3―we now need to solve our equations for lower values of μ.
Upon attempting to solve Equations (7)-(9) for μ = kθBaAs ≈ 23.6 meV, for example, we find that the second term on the RHS of Equation (9) becomes complex because of the factor ![]() (the lower limit of its integration is −kθFe ≈ −34.4 meV). Real solutions can therefore be obtained only by truncating the region of integration, i.e., by replacing (−kθFe) by (−μ). As we progressively decrease μ to move towards the ratios noted under Property (viii), additional terms in our equations need to be truncated too. Rather than addressing this problem manually as the need arises, a one-step solution is to employ real values of all the terms on the RHS of Equations (10)-(15). With this proviso, our equations can be used for any value of μ in the range considered here, which is 100 ≥ μ/(kθBaAs) ≥ 0.1. Table 1 includes the results for values of μ down to μ/(kθBaAs) = 0.2.
(the lower limit of its integration is −kθFe ≈ −34.4 meV). Real solutions can therefore be obtained only by truncating the region of integration, i.e., by replacing (−kθFe) by (−μ). As we progressively decrease μ to move towards the ratios noted under Property (viii), additional terms in our equations need to be truncated too. Rather than addressing this problem manually as the need arises, a one-step solution is to employ real values of all the terms on the RHS of Equations (10)-(15). With this proviso, our equations can be used for any value of μ in the range considered here, which is 100 ≥ μ/(kθBaAs) ≥ 0.1. Table 1 includes the results for values of μ down to μ/(kθBaAs) = 0.2.
The gist of our study so far is that we have shown that the experimental values of BaAs noted in the set of Equation (2) are explicable via values of {μ, λBa, λFe, λAs} in any row of Table 1. To make predictions following from our approach, we must now fix the value of μ. To do so we need to appeal to another property of the SC, which we choose to be j0. Before undertaking this task, to shed light on Properties (ii) and (viii) in Section 3, we recall that in a study of crossover without appeal to scattering length theory [25] , for a hypothetical system characterized by a single interaction parameter, the contributions of the hole-hole and the electron-electron scatterings to the pairing amplitude were separated and a parameter ρ was defined as the ratio of these contributions. It was then seen that the BCS state is characterized by ![]() and its progressively lower values signify a march towards the BEC end. Since we are now dealing with two interaction parameters, we adopt the following definition
and its progressively lower values signify a march towards the BEC end. Since we are now dealing with two interaction parameters, we adopt the following definition
![]() (17)
(17)
4.6. Fixing μ via the Experimental Value of j0
Employing the basic equation for j0, i.e., ![]() , where ns is number of superconducting electrons, e the electronic charge and v0 the critical velocity of electrons (which is the velocity of CPs at which the gap vanishes), the following EF-dependent equation has been derived in [24] via the same approach that led to GBCSEs, i.e., via a BSE.
, where ns is number of superconducting electrons, e the electronic charge and v0 the critical velocity of electrons (which is the velocity of CPs at which the gap vanishes), the following EF-dependent equation has been derived in [24] via the same approach that led to GBCSEs, i.e., via a BSE.
![]() (18)
(18)
where θ = θBaAs and γ and vg are, respectively, the electronic specific heat constant and the gram-atomic volume of the SC and y is a dimensionless construct:
![]() (19)
(19)
where P0 is the critical momentum of CPs at T = 0 and m* is the effective mass of an electron (we note that the value of A5 in Equation (18) is twice its value given in [24] and is its corrected value). To determine y, unlike the equation employed in [24] , we solve the following explicitly EF-dependent equation derived in [26] :
![]() (20)
(20)
where
![]() (21)
(21)
![]() (22)
(22)
![]() (23)
(23)
![]() (24)
(24)
![]() (25)
(25)
![]() (26)
(26)
and i = Ba or Fe.
Note that Re on the RHS of Equation (20) ensures that physically acceptable values of y are obtained by truncating the region of integration whenever required―just as it did for Equations (10)-(15).
Calculated via Equation (20), Table 1 includes the value of y corresponding to the values of {μ, λBa, λFe} in each row. To calculate j0 we now need the values of γ and vg, which we have taken as
![]() (27)
(27)
The value of γ above is one-fifth its value given in [21] because 1 mol of BaAs = 5 gat, and vg has been calculated by using the crystallographic data of the SC, a = 3.91 Å, c = 13.21 Å [27] , its molecular mass (M) and the knowledge that there are two formula units in its unit cell, whence we are led to density (d) as 5.913 g cm−3, and to vg via M/5d.
Calculated via Equation (18), Table 1 includes the values of j0 corresponding to the values of μ, λBa, λFe, and y in each row of it. Hence, appealing to the estimated value of j0, i.e., 2.5 × 107 Acm−2 (noted under Property (ix) in Section 3), we have for BaAs the result that
![]() (28)
(28)
5. Implications of EF = 14.2 meV for the Properties of BaAs Noted in Section 3
We have so far shown that, when EF = 14.2 meV, the values of the smaller gap and Tc in the set of Equation (2) are explicable, symbolically, via {θBa, λBa} + {θFe, λFe} in the 2PEM scenario, and the value of larger gap via {θBa, λBa} + {θFe, λFe) + {θAs, λAs) in the 3PEM scenario. Some of the results that immediately follow from this value of EF are:
(a)![]() , which agrees with the value noted under Property (x).
, which agrees with the value noted under Property (x).
(b) In the 1PEM scenario, the sub-set {θBa, λBa} leads to |W1| = 3.59 × 10−6 eV, which is in accord with Property (vi).
(c) In the 2PEM scenario, sub-sets {θFe, λFe) + {θAs, λAs) lead to |W2| = 9.08 meV, which is very close to the values reported in more than one paper, as noted under Property (vii).
(d) Calculated in the 3PEM scenario via Equation (9)―with LHS replaced by Equation (16)―the values of {θBa, λBa} + {θFe, λFe) + {θAs, λAs) lead to Tc = 51.2, in accord with Property (iv).
With EF fixed, we can calculate ρ vide Equation (17), and s (i.e., m*/me), ns, the density of superconducting electrons, and v0, the critical velocity of CPs, via the following equations [24] :
![]() (29)
(29)
![]() (30)
(30)
![]() (31)
(31)
With s also fixed, we can calculate the coherence length ξ via
![]() (32)
(32)
Before we report the values of these parameters for μ = 14.2 meV, we note that―corresponding to 2361 ≤ μ ≤ 7.08 meV, as in Table 1―they vary as follows:
![]() (33)
(33)
For μ = 14.2 meV, the values of the above parameters are:
![]() (34)
(34)
Note that: (a) the product of ns and v0 from Equations (33) and the electronic charge leads to j0 = 2.46 × 107 Acm−2, in agreement with its estimated value noted as Property (ix), (b) the value of ρ in Equation (40) is in accord with Property (ii); it also signifies that BaAs is nearly in the middle of crossover regime even though we now have Δ1/EF = 0.44 and Δ2/EF = 0.84. The differences between these values and those noted in Property (viii) could well be because our value of EF is based also on j0 of the SC, and (c) s and ξ above are in the same ballpark of values as were noted under Properties (xi) and (xii), respectively.
6. Discussion
1) A key step of our approach is the “resolution” of θBaAs into θBa, θFe and θAs. We draw attention in this connection to a paper by Kwei and Lawson [28] where, based on neutron powder diffraction experiments, it has been reported that constituents of La2CuO4 do indeed have different Debye temperatures.
2) Dictated by the need to avoid complex-valued solutions, truncation of some of the integrals is another key step of our study. To makes this step physically plausible, let us consider a convoy passing through a range of mountains. As the road twists and turns through a series of valleys and hill-tops, the sunlight it receives will vary from a maximum at the highest point of the range to a minimum determined by its overall topography. Streams of itinerant conduction electrons on the 3-d Fermi surface of an SC in the backdrop of various ion species are akin to such a convoy: there will be places where the available range of phonon energies for pairing from one or the other species of ions is depleted. Recent experimental work of Tacon et al. [29] dealing with YBa2Cu3O6.6 lends credence to this view.
3) Our considerations so far have been based on the Debye temperatures of various ions as noted in the set of Equation (1). In view of the analogy given above, we now report our findings based on a different set, which too follows from θBaAs = 274 K by considering the layered structure of the SC [22] :
![]() (35)
(35)
Assuming that the smaller gap is due to phonon exchanges with the Ba and As ions, we now need to fine tune it to 6.35 meV in order that all the λ values satisfy the Bogoliubov constraint for any μ in the range100 ≥ μ/kθBaAs ≥ 0.1. For μ/kθBaAs = 0.6, we obtain
![]() (36)
(36)
Then, with![]() , some of our results are:
, some of our results are:
(a) ![]()
(b) In the 1PEM scenario, {θBa, λBa} values lead to |W1| = 5.9 meV and {θAs, λAs) to |W1| ≈ 0.
(c) In the 2PEM scenario, {θFe, λFe) + {θAs, λAs) values lead to |W2| = 9.0 meV.
(d) In the 3PEM scenario, {θBa, λBa} + {θFe, λFe) + {θAs, λAs) values lead to Tc = 52.7 K.
4) From our findings based on Tc = 37 K and the two sets of values of {θBa, θFe, θAs} derived from θBaAs and the facts that (a) Tc of the SC can vary between 36 and 38 K and (b) θBaAs also leads to additional values for the set {θBa, θFe, θAs} as given in [22] , it follows that GBCSEs can shed light on the multitude of ∆s that have been reported for this SC; see also [30] in this connection where multiple gaps of La2CuO4 have similarly been dealt with. We are not aware if this feature of multi-gap SCs has been addressed via any other approach.
5) We now deal with the feature of the dome-like structure exhibited by BaAs that was noted as Property (xiii) in Section 3. To address this feature, we refer to the row corresponding to ![]() in Table 1 where λBa = 0.1155 and λFe = 0.3838. Considering the analogy given above, if we assume that as μ fluctuates in the range
in Table 1 where λBa = 0.1155 and λFe = 0.3838. Considering the analogy given above, if we assume that as μ fluctuates in the range ![]() the values of λFe change as given in Table 1 (i.e., by employing λFe as the tuning variable), but λBa remains frozen at 0.1155, then the values of Tc calculated vide Equation (9) yield the plot given in Figure 1.
the values of λFe change as given in Table 1 (i.e., by employing λFe as the tuning variable), but λBa remains frozen at 0.1155, then the values of Tc calculated vide Equation (9) yield the plot given in Figure 1.
![]()
Figure 1. Plot of Tc vs. x ≡ μ/kθBaAs for 0.9 ≤ x ≤ 0.3 obtained by solving Equation (7) for pairing via the Ba and the Fe ions by employing values of λFe as in Table 1 and keeping λBa fixed at its value corresponding to μ/kθBaAs = 0.6 (dashed curve). The solid curve is for pairing via the Ba and the As ions with a fixed value of λAs (corresponding to μ/kθBaAs = 0.6), but different values of λBa.
Given also in this figure is a similar plot when pairing is assumed to take place via the Ba and the As ions, and λAs is kept fixed at its value corresponding to![]() , but λBa is varied.
, but λBa is varied.
7. Conclusions
1) We have shown that the values of Δs, Tc and j0 of BaAs are correlated via the values of λBa, λFe and λAs that the μ-incorporated GBCSEs lead to. To shed light on various other properties of the SC noted in Section 3, we needed to fix the value of μ. We were guided in this task by a crossover study of the SC. This however is not an essential step of our approach because we could, alternatively, have fixed μ by invoking Property (x).
2) We have shown that EF plays a fundamental role in determining the ∆s, Tc, j0, m*, v0, ns, ρ, and ξ of an SC. Since j0 is not an intrinsic property of SCs, our work suggests that by varying μ in an appropriate range and using as input the θ, ∆s and Tc values of different SCs, construction of a table of values of j0, m*, v0, ns, ρ, and ξ for each of them would be handy. Appeal to the experimental value of j0 can then fix the values of μ and other parameters of the SC and may yield plausible clues about how its j0 (and hence Tc [24] ) may be enhanced.
3) In so far as the truncation of the BCS equations was also needed while dealing with the heavy-fermion SCs [31] for which it is known that μ < kθ, it follows that GBCSEs provide a common canopy for both high-Tc SCs and the so-called exotic or unconventional SCs.
4) In the context of the yet unresolved issue of the mechanism of pairing in composite SCs, we should like to draw attention to the fact that GBCSEs imply that more than one mechanism may be at work in any such SC. To elaborate, in the 2PEM scenario, for example, GBCSEs invoke two interaction parameters, ![]() and
and![]() . For the sake of generality, one may assume that the interaction energies between electrons bound as CPs, V1 and V2, are given by
. For the sake of generality, one may assume that the interaction energies between electrons bound as CPs, V1 and V2, are given by ![]() and
and![]() , where V10 and V20 are the usual phononic BCS interaction terms due to the two ion-species and U1 and U2 are terms that depend upon the specifics of the constituents of the SC. If U1 = U2 = 0, then of course we have superconductivity caused only by phonons. If not, even when only one of the U’s has non-zero value, we have a situation where the glue provided for the formation of CPs is provided by more than one mechanism.
, where V10 and V20 are the usual phononic BCS interaction terms due to the two ion-species and U1 and U2 are terms that depend upon the specifics of the constituents of the SC. If U1 = U2 = 0, then of course we have superconductivity caused only by phonons. If not, even when only one of the U’s has non-zero value, we have a situation where the glue provided for the formation of CPs is provided by more than one mechanism.
We conclude by noting that the derivations of most of the equations employed in this paper and the concepts on which they are based, e.g., multiple Debye temperatures, superpropagator, and the Bogoliubov constraint, can be found at one place in [23] .
Acknowledgements
The author thanks Professor D.C. Mattis for correspondence which led him to the approach he has followed in this and some of his earlier papers. He also thanks Professor M. de Llano and Mr. I. Chavezfor drawing his attention to [15] .
NOTES
![]()
Iron-based superconductors.