1. Introduction
Maxwell extended Ampere’s circuital law by adding a time derivative electric displacement term accounting for the polarization of material in a capacitor, thus balancing an incoming electric current [1] . This electric displacement is incorporated in the modern macroscopic set of Maxwell’s equations where two important types of charges are defined: free charges and bound charges. Utilizing these two forms of charge density allows the macroscopic set of Maxwell’s equations to describe the large scale behaviour of matter without considering all of the atomic scale details. Alternatively, the microscopic set of Maxwell’s equations is applicable in a vacuum, which considers the total charge. This paper asks if difficulties associated with the macroscopic description of electric fields in an electrolyte may be solved by defining a new form of charge density: the mobile charge density.
Publications and reviews regarding electrochemical systems and the coupled electric field are plentiful. Prentice and Tobias [2] presented a comprehensive review of theory explaining many aspects of electrochemical systems, including electrochemical reaction rates, electrolytic transport, and coupled electric fields. Dukovic [3] also presented a review of methods for computing current distributions and assumed that the electric field in an electrolyte could be represented by Laplace's equation (provided uniform conductivity existed) along with Ohm’s law to describe electric current. However, a very meticulous and comprehensive treatment of electrochemical systems, including the coupled electric field, is provided by Newman and Thomas-Alyea’s textbook [4] . Newman and Thomas -Alyea discuss the electric state of electrolytes and utilize Gauss’s law from Maxwell’s equations as the foundational theory to which additional assumptions or neglections provide multiple approaches to incorporate electric field effects.
1.1. A Macroscopic Form of Maxwell’s Equations
In 1864 James Maxwell presented nine equations summarizing all known laws on electricity and magnetism [1] . These equations may be presented in a number of different forms. The macroscopic Maxwell-Minkowski form consists of four field equations [5] :
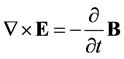 (1)
(1)
 (2)
(2)
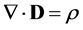 (3)
(3)
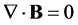 (4)
(4)
and the continuity equation:
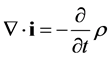 (5)
(5)
For a linear isotropic material the Electric Displacement Field is [5] :
 (6)
(6)
where, the second term on the right-hand-side is the polarization vector,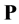 . The polarization vector represents a response of bulk molecules to an applied electric field. The polarization or distortion of these molecules creates an electric field that opposes the applied electric field.
. The polarization vector represents a response of bulk molecules to an applied electric field. The polarization or distortion of these molecules creates an electric field that opposes the applied electric field.
1.2. Methods for Modeling Electrolytes and Electric Fields
Newman and Thomas-Alyea state that “no quantitative characterization or measure of the difference of electrical state of two phases has yet been given when the phases are of different chemical composition” [4] . Electrochemical theory contains multiple equations dealing with the electric field and charge density that encompass different strategies, including: Poisson’s equation, Laplace’s equation, electroneutrality, Ohm’s law, and the Nernst equation.
1.2.1. Nernst-Planck-Poisson Equation
Poisson’s equation, describing the electric field, may be derived from Gauss’s law in Maxwell’s equations. Poisson’s equation describes the Laplacian of electric field as a function of charge density and permittivity. Therefore, to calculate an electric field using Poisson’s equation the charge density distribution must be known or predicted/modeled simultaneously with an additional equation. An equation, such as the Nernst-Planck equation, is capable of modeling flux and ionic current to predict a charge density distribution in electrolytes. An extensively published model for electrolytes couples these two equations and is commonly known as the Nernst-Planck-Poisson equation set, describing coupled transport and the electric field. However, in certain scenarios this method has the disadvantage of requiring very small time steps, sometimes approaching the order of approximately 10−12 seconds, as the resulting equations are considered to be mathematically stiff [6] .
1.2.2. Dilute Solution Theory
Due to difficulties in solving transport equations coupled with Poisson’s equation other theories have been presented upon which models may be founded. One widely used theory in the open literature is dilute solution theory [4] . Dilute solution theory utilizes a flux or transport equation coupled with information describing the electric state of the electrolyte/system. For the many models based on dilute solution theory, this information may take the form of boundary conditions, assumed electroneutrality, Laplace’s equation, a known/fixed ionic current, or other equations/assumptions. However, Poisson’s equation is considered the foundational equation describing the electric field and other mechanistic methods are usually either founded on or related back to Maxwell’s equations. For example, Newman and Thomas-Alyea validate the electroneutrality assumption through a comparison of resulting concentration gradients utilizing the more fundamental Poisson’s equation [4] . Moderately dilute solution theory is based on dilute solution theory by incorporating activity coefficients.
1.2.3. Concentrated Solution Theory
Concentrated solution theory [4] provides an equation describing transport of species and incorporates additional interaction between ions through additional experimental information. This additional experimental information takes the form of multiple transport properties: the conductivity, the diffusion coefficient, and the transference number. Concentrated solution theory may then model ionic transport while incorporating some degree of ionic electric interaction for- ces. However, knowledge of all transport properties for all scenarios requires a large amount of experimental data or additional empirical equations which may sometimes cause difficulties [7] .
The objective of this research is to overcome difficulties in conventional theory describing electrolytes and the coupled electric field. Specifically, can a general definition of electric potential be developed that requires fewer assumptions than conventional theory and also requires fewer experimentally determined transport properties? A secondary objective of this theory is to investigate the relationship of this new theory with Maxwell’s equations and to determine if Maxwell’s equations may be further generalized.
2. Theory
This section will explore the application of coupled equations for transport and the electric field. Although examples are provided, the concepts presented are expected to extend beyond the case of electrolytes and beyond the specific equations utilized. In Section 2.1 and Section 2.2, equations are arranged such that phenomenological issues may be apparent. These issues are not incorporated into the final model presented in this paper. Instead, the author proposes these difficulties are inherent in conventional theory. The only conclusion drawn from Section 2.1 is that the Nernst-Planck equation depends upon a time step to predict an electric displacement and Poisson’s equation does not. Section 2.2 concludes that to create a parallel kinetic model a poor assumption regarding displacement is required. Section 2.3 explores similarities between kinetic models regarding displacements and conventional models for electric displacement. Section 2.4 utilizes these similarities to define a new form of mobile charge density and Section 2.5 develops a model for the electric field when the actions causing electric displacement are described by a transport equation. Section 2.6 presents the Inherent Charge Density model.
2.1. Coupling Poisson’s Equation with a Transport Equation
A very well published method for modeling charge in an electrolyte is the Nernst-Planck-Poisson equation set. This method couples the Nernst-Planck equation with Poisson’s equation for the electric field. Although the following investigation will be focused on the Nernst-Planck-Poisson equation set, it should be equally valid for any dynamic transport equation coupled with electrostatics.
2.1.1. Theoretical Difficulties and the Time Step
The Nernst-Planck equation describes flux. In this description, the two phenomena creating flux are electro migration due to an electric field and diffusion due to a concentration field and are represented in the equation:
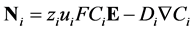 (7)
(7)
Poisson’s equation, developed from Gauss’s law, is:
 (8)
(8)
When no reactions are occurring, conservation of species provides:
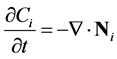 (9)
(9)
Taking the divergence of Equation (7), combining with Equation (9), multiplying both sides by 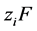 and summing over all species gives:
and summing over all species gives:
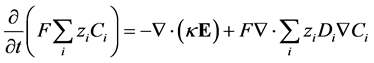 (10)
(10)
where,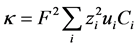 . Integrating over time and incorporating the definition of charge density,
. Integrating over time and incorporating the definition of charge density, 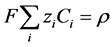 , gives:
, gives:
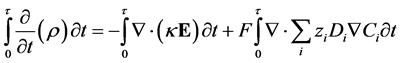 (11)
(11)
Substituting the definition of electric displacement from Maxwell’s equations (Equation (3)) into Equations (8) and (11) gives a rearranged form of the Nernst-Planck-Poisson equation set:
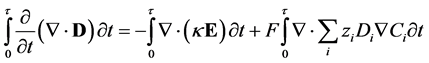 (12)
(12)
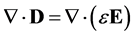 (13)
(13)
When applying the Nernst-Planck-Poisson equation set, the transport equation must be integrated over a time step to create a charge density distribution utilized as the independent variable in Poisson’s equation to then calculate the resultant electric field. With this in mind, for a first time step where the composition of the electrolyte is initially homogeneous, isotropic and electroneutral, Equations (12) and (13) simplify to:
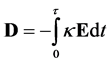 (14)
(14)
![]() (15)
(15)
Interestingly, comparing these equations shows that both Equation (14) and (15) demonstrate an electric displacement proportional to the electric field; however, three differences are apparent:
1) The proportionalities are of different sign
2) The proportionality constants may be different
3) The electric displacement predicted by Equation (14) depends upon the integration time step,![]() .
.
Several arguments might be made to theoretically explain: 1) why the proportionalities are of different sign and 2) why the proportionality constants may be different. These items will be dealt with later in this paper. At this stage the discussion is limited to the fact that the transport equation depends upon integration over a time step and Gauss’s law does not. Therefore, for Equations (14) and (15) to obey Newton’s third law that every reaction has an equal and opposite reaction, the time constant must be specified. Specifically, where the electric field and conductivity are assumed constant over the integration time period:
![]() (16)
(16)
2.1.2. Time Step and Newton’s Third Law
The following example illustrates underlying issues with the Nernst-Planck- Poisson equation set and tests Equation (16). Consider a rectangular vessel containing 0.1 mole/m3 of AgNO3 and split into two cubic control volumes with 0.5 cm sides (shown in Figure 1). Ionic transport will arise if 1 Volt is applied over
![]()
Figure 1. AgNO3 electrolyte with two control volumes.
these two control volumes for 5 seconds. Under these conditions the Nernst- Planck equation predicts a charge density of 266.62 C/m3 in each control volume after 5 seconds. According to Poisson’s equation, this charge density corresponds to a voltage of −9.614 × 106 V across the system. Alternatively, if the time step is calculated according to Equation (16), then,
![]() . When the Nernst-Planck equation is
. When the Nernst-Planck equation is
applied for the same situation over 5.201 × 10−7 seconds, 2.773 × 10−5 C/m3 of charge is predicted at each node. According to Poisson’s equation, this charge density corresponds to a voltage of −1.000 V. In this case, incorporating Equation (16) ensured the adherence of Newton’s third law.
This section illustrated how the charge density predicted by the Nernst-Planck equation depends on the time over which the resulting transport equation is integrated and Poisson’s equation does not. This time step issue must be true for any dynamic transport/flux equation coupled with a static equation and is not limited to the specific equations or scenario provided here. If the correct time step is not calculated and used for every an iteration of the Nernst-Planck-Poi- sson equation set, Newton’s third law may not be guaranteed.
2.2. Coupling Hooke’s Law with Transport
The following example utilizes a poor assumption to develop models regarding displacement that may be similar to models for electric displacement outlined in Section 2.1. It will be shown how both equation sets depend similarly on a specific time period to obey Newton’s third law. Consider a cart moving horizontally at a constant velocity in a linearly resistive medium, shown in Figure 2. A force is applied to the cart through a spring to counter the resistance and maintain the cart’s constant velocity. The force in the spring is given by Hooke’s law:
![]() (17)
(17)
The linear resistive force is given:
![]() (18)
(18)
For the system to be at steady-state and constant velocity, the spring and drag
![]()
Figure 2. A cart propelled at constant velocity under linear resistance.
forces must be equal to some force,![]() . Also, if it is assumed that the displacement,
. Also, if it is assumed that the displacement, ![]() , may describe both the displacement of the spring and the displacement of the cart over an initial time step (where
, may describe both the displacement of the spring and the displacement of the cart over an initial time step (where![]() ), then we may rearrange Equations (17) and (18) and integrate Equation (18) over time to obtain two equations:
), then we may rearrange Equations (17) and (18) and integrate Equation (18) over time to obtain two equations:
![]() (19)
(19)
![]() (20)
(20)
For Equations (19) and (20), Newton’s third law is only guaranteed when:
![]() (21)
(21)
This cart example demonstrates a poor assumption: that the value for displacement of the cart may be interchanged with value for displacement of the spring. A better method for modeling the cart would be to realize that although the same applied force is balanced with both the stretching of the spring and the velocity of the cart, the resulting displacements, ![]() , in Equations (19) and (20), should be represented as two different vectors, with two different frames of reference, for displacements of two different objects. Also, similar to Equation (16), Equation (21) shows that if the displacements are assumed to be interchangeable, Newton’s third law is only guaranteed for a specific time period.
, in Equations (19) and (20), should be represented as two different vectors, with two different frames of reference, for displacements of two different objects. Also, similar to Equation (16), Equation (21) shows that if the displacements are assumed to be interchangeable, Newton’s third law is only guaranteed for a specific time period.
2.3. What Type of Electric Displacements May Occur in an Electrolyte?
Figure 3 schematically represents phenomenological and mathematical similarities between kinetic and electric phenomena for an isotropic medium. This figure shows Gauss’s law has similarities with Hooke’s law. Hooke’s law, shown in Figure 3(a), demonstrates both the applied force (action) and opposing force within the spring (reaction) are proportional to the displacement, or stretching, of the spring, but of opposite sign. This may answer the question of why Equation (14) and Equation (15) are of opposite sign, since every action should be coupled with an equal and opposite reaction. Figure 3(b) demonstrates the electric displacement inherent in Gauss’s law under the action of an electric field, and Figure 3(c) how the time derivative of electric displacement is electric current. Also demonstrated are similarities between Ohm’s law and an object in a
![]()
Figure 3. Phenomenological and mathematical similarities between kinetic and electric phenomena for an isotropic medium where the “action” is causing a displacement or motion and the “reaction” is equal and opposite. The phenomenological models are: (a) spring model―Hooke’s law; (b) electric displacement―Gauss’s law; (c) electric current―time derivative of Gauss’s law; (d) constant velocity in linearly resistive medium―kinetics; (e) electric current―Ohm’s law; and (f) electric displacement―time integral of Ohm’s law.
linearly resistive medium. Figure 3(d) shows how, for an object in a linearly resistive medium, the force is proportional to the velocity of the object, and Figure 3(e) shows that when Ohm’s law is applicable the electric field acts proportionally to the electric current, where the proportionality constant is the inverse of conductivity. Finally, Figure 3(f) demonstrates an electric current integrated over a time period causes an electric displacement, mathematically similar to integrating a velocity over a time period to calculate a displacement.
Figure 3 demonstrates that Equation (14) and Equation (15) are related in exactly the same manner as Equation (19) and Equation (20), because Equation (14) and Equation (19) describe a displacement due to constant motion/velocity applied over a time period and Equation (15) and Equation (20) describe a balanced static displacement with zero velocity. The mathematical similarities between the kinetic and electric phenomena presented in Figure 3, coupled with the poor assumption made in Section 2.2 of interchangeable displacement, may result in the question: is the electric displacement predicted by a transport equation interchangeable with the electric displacement described by Gauss’s law?
2.4. Possible Forms of Electric Displacement/Charge Density in an Electrolyte
Multiple forms of charge density may be simultaneously apparent in an electrolyte. Do these forms actually exist, or are they simply manifestations of phenomenological models and numerical procedures? Does it matter? In the phenomenological model presented here, it is suggested that ions in an electrolyte may react to an electric field in the manner shown in Figure 4, for an isotropic medium. Figure 4 shows that an electric displacement may be created by the electric field proportional to the permittivity of the material. This first case of electric displacement considers the electric displacement apparent in a vacuum and electric displacement caused by polarization of molecules/ions. The divergence of this first form of electric displacement creates free and bound charge density. However, Figure 4 also considers another form of electric displacement caused by integrating electric current or applying a transport equation over a time step. Since this paper has proposed that not all electric displacements may be interchangeable, to enhance distinguishability, the divergence of this additional form of electric displacement created by the movement of mobile charges (ions) will be named: mobile charge density. The phenomenological mechanism behind each electric displacement and creation of each form of charge density is different (as shown in Figure 3). The total divergence of electric displacement could be calculated by summing all three types of charge density (bound and free are combined in the first term on the right-hand-side):
![]() (22)
(22)
2.5. Mobile Charge Density and Electrolytic Transport
This section will utilize the concept that multiple forms of charge density may exist in an electrolyte; however, an electrolytic transport equation will predict mobile charge density created by the movement of ions and transport equations do not generally simulate the polarization of bulk molecules. A transport equation which considers flux due to electromigration, diffusion, and activity coefficients is given:
![]() (23)
(23)
Additionally, a material balance considering reactions:
![]()
Figure 4. Different forms of electric displacement in an isotropic medium.
![]() (24)
(24)
By combining Equations (23) and (24), multiplying both sides by ![]() and summing over all species gives:
and summing over all species gives:
![]() (25)
(25)
where, ![]() , is the conductivity. Using the concept of mobile charge density to explain Equation (25); (mobile) charge density may be created due to an electric field, diffusion, activity coefficent gradients, and the production or consumption of ions. Comparing with concepts presented in Figure 3 and incorporating Newton’s third law, each of the terms on the right-hand-side can be thought of as an action causing electric current (or electric displacement if applied over a period of time), phenomenologically similar to forces acting on a particle in a linearly resistive medium. If Newton’s third law holds, then there should be an equal and opposite reaction to each action. Figure 5 incorpotates Newton’s third law showing an equal and opposite reaction for the transport equation, Equation (25).
, is the conductivity. Using the concept of mobile charge density to explain Equation (25); (mobile) charge density may be created due to an electric field, diffusion, activity coefficent gradients, and the production or consumption of ions. Comparing with concepts presented in Figure 3 and incorporating Newton’s third law, each of the terms on the right-hand-side can be thought of as an action causing electric current (or electric displacement if applied over a period of time), phenomenologically similar to forces acting on a particle in a linearly resistive medium. If Newton’s third law holds, then there should be an equal and opposite reaction to each action. Figure 5 incorpotates Newton’s third law showing an equal and opposite reaction for the transport equation, Equation (25).
Therefore, from Figure 5 and Newton’s third law, the reaction to the transport equation may be found by taking the negative value of the actions on the right-hand-side of Equation (25):
![]() (26)
(26)
Equation (26) can be rearranged to provide the electric field resulting from transport calculated using Equation (25); in other words Equation (26) can be rearranged to calculate the electric field resulting from diffusion potential, activity coefficients, creation or consumption of ions, and mobile charge density.
2.6. Inherent Charge Density Model
The previous section presented a flux equation, coupled with the continuity equation, and an equation for the electric field developed by extending the phenomenological model of Maxwell. These two equations will now be rearranged and presented together as an equation set describing the transport (from combining Equation (23) and (24)) and coupled electric field, respectively,
![]()
Figure 5. Schematic showing the reaction to each action caused by a transport equation.
(where![]() ):
):
![]() (27)
(27)
![]() (28)
(28)
This equation set is an Inherent Charge Density model and it may be implemented multi-dimensionally using the following boundary conditions, for Equation (27) and (28), respectively, in the appropriate dimensions:
![]() (29)
(29)
![]() (30)
(30)
3. Validation
Validations and simulations already conducted for the Inherent Charge Density model are too lengthy for a single publication. Therefore, this section will present some new validations with a brief mention of other validations available in the open literature. Interestingly, the same governing equations and the same boundary conditions may be used for all scenarios. The first test of the Inherent Charge Density model and underlying theory is to examine whether the predicted electric field is dependent upon the time step over which the transport equation is applied. Therefore, Equations (27) and (28) are applied to the same problem as examined earlier in this paper, presented in Figure 1, where an electric field of 1 V is applied. In this case, the transport equation, Equation (27), predicts 266.62 C/m3 in each control volume after 5 seconds. Upon application of Equation (28) over a time of 5 seconds a value of −1.000 V is calculated for the electric field. This demonstrates that the strength of the response of the electrolyte, in terms of electric field, is of similar magnitude to the strength of the applied action and Newton’s third law is obeyed.
Additional validations and results from numerical simulations using the Inherent Charge Density Model have been presented. Kennell [8] demonstrated the electric potential over various different liquid junctions calculated using the Inherent Charge Density model matched very closely the values experimentally measured and calculated using alternate methods. Additionally, Kennell [8] demonstrated that dynamic liquid junction potentials were simulated, along with realistic transport, over an extended period of time. Specifically, as the liquid junction region grew over time, so did the corresponding region of potential gradient (although the total potential difference remained constant). Also, Kennell showed that the thickness of the region of varying concentration varied proportionally to the square root of time, as expected for dynamic liquid junctions [8] .
Kennell [8] also conducted a validation of the Inherent Charge Density Model involving a moving liquid junction and ionic current previously presented by Fu and Chan [9] . In this case, silver ions were produced due to an electrochemical reaction into one end of a glass tube. The ionic current caused by the silver dissolution caused an experimentally visible liquid junction to move at a measured rate down the glass tube. Kennell [8] demonstrated a successful validation of the Inherent Charge Density Model in this scenario, but also expanded the model multi-dimensionally and presented multi-dimensional electric fields balanced with multi-dimensional ionic fluxes and concentration gradients.
The Inherent Charge Density Model has also been applied to more complex scenarios, including a lithium-ion battery undergoing charging, with details available elsewhere [10] . Figure 6 shows the simulated dynamic electric field across an electrolyte of a lithium-ion battery where the electrolyte extends beyond the ends of the equal length anode and cathode. The numerical procedure used time steps of 0.001 seconds. Therefore, there were 3.6 × 106 stable sequential iterations of the Inherent Charge Density model to create the data displayed in Figure 6. Additionally, along the surface of the anode and cathode Tafel kinetics were assumed for electrochemical reactions that were dependent on the concentration of species and the electric potential of the adjacent electrolyte relative to that of each electrode. Although this may appear to be too many degrees of freedom for calculations of this type, it resulted in a stable numerical procedure and equal charging electric current along the total length of both electrodes of 4.37 Am−2. A more complete examination of the dynamic electric
![]()
![]()
Figure 6. Simulated electric potential field in lithium-ion battery electrolyte, with extension past electrode ends, after 1 hour of charging as (a) surface plot and (b) a contour plot with cell geometry.
field coupled with ionic transport and non-homogeneous properties in the electrolyte and electrodes can be found elsewhere [10] .
4. Discussion
Investigations demonstrated that an electric current integrated over a time period causes an electric displacement. Divergence of this electric displacement may cause charge density. Gauss’s law assumes charge density is stationary and in balance with the electric field. Ohm’s law assumes charges are in uniform motion. By assuming Newton’s third law should be valid for a charge/ion, whether stationary or in motion, a transport equation was modified by changing the sign of the charge density term, creating an Inherent Charge Density Model. The Inherent Charge Density model was developed without assuming electroneutrality or electrostatics. The main weaknesses of the model pertain to the flux equation upon which the development was founded. However, the theory and process demonstrated here could be applied to alternate transport models. The Inherent Charge Density model was validated for a number of liquid-junctions, balanced ionic current/moving liquid-junction, and a lithium-ion battery. However, two questions remain to be answered:
1) Does the Inherent Charge Density Model conflict with Maxwell’s equations?
2) How can possible discrepancies be resolved?
4.1. Conflict with Maxwell’s Continuity Equation
It may appear that Equation (22) conflicts with the continuity equation from Maxwell’s equations. This is because Equation (28), in the absence of reactions, can be rewritten as:
![]() (31)
(31)
Equation (31) appears to conflict with Maxwell’s continuity equation, Equation (5), due to the absence of a negative sign. However, it has been shown various times in this paper that a negative sign may be due to Newton’s third law, where a reaction should be equal but opposite to an action.
In the case when Maxwell extended Ampere’s circuital law by adding a term to account for the divergence in electric displacement caused by dynamic bound charge density in a solid capacitor, the electric current and bound charge density were situated at physically adjacent locations; the electric current was occurring in a conductor and the bound charge density was located in a capacitor. The conductor and capacitor were adjacent and connected. Figure 7 shows the phenomenological models for adjacent and connected kinetic and electric phenomena. Figure 7(a) shows four particles connected by two springs and a non-elastic connection. The particle on the left is subject to a constant force and the particle on the right is fixed and stationary. A free body diagram for the steady-state kinetic scenario is shown in Figure 7(b) and demonstrates two equal and opposite forces on the central two particles. Figure 7(c) shows a phenomenologically
![]()
Figure 7. Phenomenological and mathematical similarities between kinetics and electric phenomena involved in the continuity equation. The various aspects include: (a) applied force on two connected springs in series; (b) free body diagram around central connected static particles; (c) applied electric field on conductor connected with capacitor; and (d) balance around connection between conductor and capacitor.
similar model for electric displacements in a conductor adjacent to a capacitor. In Figure 7(c) the electric current applied to the conductor may be considered the action on the system. Figure 7(d) demonstrates that the actions within the conductor must be balanced by an equal and opposite reaction within the capacitor, and this requires the two balanced terms to be of opposite sign, agreeing with the continuity equation, Equation (5). However, Equation (28) does not represent electric displacement/current occurring at adjacent locations. Instead, Equation (28) represents electric current causing equivalent time derivative of electric displacement occurring at the same location, and not adjacent phenomena balanced with each other. For this reason, the negative sign in Equation (5) representing a reaction to an action is absent from Equation (31). It may therefore be concluded that the Inherent Charge Density model is not in conflict with the continuity equation.
4.2. Extending Maxwell’s Equations
In an electrolyte, electric displacement may be caused by multiple phenomena and charge density may be balanced with the electric field via Ohm’s law and/or Gauss’s law. By assigning a third form of charge density, called mobile charge density, it becomes possible to distinguish between different forms of electric displacement and different phenomena. Kennell [8] presented similar equations to balance phenomena when electric current and charge density may be numerically predicted to occur concurrently, balanced with the same electric field, at the same physical location:
![]() (32)
(32)
![]() (33)
(33)
![]() (34)
(34)
![]() (35)
(35)
where, the total charge density is the sum of the free, bound, and mobile charge density:
![]() (36)
(36)
![]() (37)
(37)
![]() (38)
(38)
4.3. Deriving the Continuity Equation from Extended Maxwell’s Equations
It is expected that extending Maxwell’s equations to incorporate the charge density calculated from integrating an electric current over a time period will not detract from their general and wide applicability. Also, one of the important accomplishments of Maxwell’s original equations was that the continuity equation could be derived from the equations. It will now be shown that the continuity equation can still be derived from the extended equations show in Section 4.2. The divergence of Equation (33) gives:
![]() (39)
(39)
The left-hand-side of Equation (39) is zero. Incorporating Equation (34) into Equation (39) gives:
![]() (40)
(40)
Inserting Equations (36) and (38) into Equation (40) provides the continuity equation, where the sum of free and bound charge density represents the electric displacement occurring within a capacitor:
![]() (41)
(41)
Therefore, the theory presented in this paper does not appear to be in conflict with Maxwell’s equations. Instead, by acknowledging the fact that electric current applied over a time period causes electric displacement, and incorporating Newton’s third law, a more general form of Maxwell’s equations has been presented that resolves possible discrepancies and/or difficulties.
5. Conclusions
It was shown that coupling Gauss’s law with a transport equation (such as in the Nernst-Planck-Poisson equation set) may violate Newton’s third law. This is because the electric field calculated by Gauss’s law depends upon the divergence of electric displacement, or charge density, which calculated by integrating the transport equation over a period of time. Not only must the time period be very small, but for Newton’s third law to hold the time step would have to be accurately calculated for each iteration, assuming a dynamic non-homogenous pha- se(s). To rectify this problem the assumption was made that Newton’s third law should be incorporated and all reactions should have an equal and opposite reaction, which resulting in the Inherent Charge Density model. Validations and simulations for the Inherent Charge Density Model demonstrated the model’s ability to model multi-dimensional multi-component electrolytes whilst considered the effects of concentration gradients, the electric field, charge density, activity coefficients, ionic currents, and balanced but physically displaced electrochemical reactions.
The Inherent Charge Density model was developed by assuming a valid transport equation and that Newton’s third law should be applied. This model was validated. The subsequent discussion presented a theory that has not yet been validated, but lays the foundation to view Maxwell’s equations from a different perspective. This theory suggests the electric displacement or charge density calculated from integrating an electric current over a period of time has a different proportionality constant (conductivity) with the electric field than the static charge density balanced in steady-state displacement with the electric field (permittivity). In other words, both Ohm’s law and Gauss’s law need not be simultaneously assumed to represent the same electric displacement caused by the same electric field. This modification does not conflict with Maxwell’s equations. Instead, this modification extends Maxwell’s equations to a more general form and it is expected that the modification will not change the generally wide applicability of these equations.
Acknowledgements
St. Peter’s College, Muenster, SK, provided publishing funding. The author would like to thank the following researchers for feedback and advice during the creation of this manuscript: Professor Richard Evitts, Dr. Jim Zacaruk, Professor Adam Bourassa, and Professor Allan Dolovich.
Nomenclature
![]() Magnetic field (V∙s/m2)
Magnetic field (V∙s/m2) ![]() Mobility (m2∙mol/J∙s)
Mobility (m2∙mol/J∙s)
![]() Concentration (mol/m3)
Concentration (mol/m3) ![]() Velocity (m/s)
Velocity (m/s)
![]() Diffusion coefficient (m2/s)
Diffusion coefficient (m2/s) ![]() Charge number
Charge number
![]() Electric displacement field (C/m2)
Electric displacement field (C/m2)
![]() Electric field (V/m)
Electric field (V/m) ![]() Permittivity (C/V∙m)
Permittivity (C/V∙m)
![]() Faraday’s constant (96,487 C/equiv)
Faraday’s constant (96,487 C/equiv) ![]() Permittivity of free space (C/V∙m)
Permittivity of free space (C/V∙m)
![]() Force (N)
Force (N) ![]() Electric potential (V)
Electric potential (V)
![]() Magnetizing field (A/m)
Magnetizing field (A/m) ![]() Conductivity (Ω−1・m−1)
Conductivity (Ω−1・m−1)
![]() Current density (A/m2)
Current density (A/m2) ![]() Charge density (C/m3)
Charge density (C/m3)
![]() Species flux (mol/m2∙s)
Species flux (mol/m2∙s) ![]() Bound charge density (C/m3)
Bound charge density (C/m3)
![]() Polarization (C/m2)
Polarization (C/m2) ![]() Free charge density (C/m3)
Free charge density (C/m3)
![]() Displacement (m)
Displacement (m) ![]() Mobile charge density (C/m3)
Mobile charge density (C/m3)
![]() Reaction source or sink (mol/m3∙s)
Reaction source or sink (mol/m3∙s) ![]() Total charge density (C/m3)
Total charge density (C/m3)
![]() Time (s)
Time (s) ![]() Time period (s)
Time period (s)