Mixed Convection and Heat Transfer Studies in Non-Uniformly Heated Buoyancy Driven Cavity Flow ()
1. Introduction
In order to fill the gap between the results of numerical simulations and experiments, several factors have to be considered and one among them is the accuracy and reliability of numerical scheme employed in the simulations. If we use the traditional second order accurate central difference method, they suffer from computational instability and may not converge when convective terms dominate. While the upwind method suppresses the unwanted physical oscillations and enables us to get solutions for a large range of cell Reynolds numbers, the major disadvantage associated with the upwind method is that its order of accuracy is very low, which is  where
where  is the grid size. In the past, in order to get optimal solution for the wide range of parameters, researchers generate benchmark results by applying the central difference operator to diffusion terms and upwind to convection dominated part of the governing equation [1] . Recently higher order finite difference schemes have gained importance due to their interesting properties such as unconditional stability, computational cost, effectiveness and hence efficiency in solving non-linear problems.
is the grid size. In the past, in order to get optimal solution for the wide range of parameters, researchers generate benchmark results by applying the central difference operator to diffusion terms and upwind to convection dominated part of the governing equation [1] . Recently higher order finite difference schemes have gained importance due to their interesting properties such as unconditional stability, computational cost, effectiveness and hence efficiency in solving non-linear problems.
The study of recirculation of the fluid inside a square cavity forms the basis to many applications including energy engineering, nuclear reactor [2] , cooling of electronic devices [3] [4] [5] , the study of chaotic mixing [6] , production of plane glass, study of coupling between evaporation and condensation [7] , and in understanding dynamics of water in lakes and ponds [8] . In particular, if the viscosity of the fluid is strongly temperature dependent, then buoyancy effects mix with the inertial effects, leading to complex flow dynamics. In the fluid flow, if the natural buoyancy driven effect and forced shear driven convection effect have comparable magnitude, we have the mixed convective heat transfer. Experimental results on the mixed convection in the bottom-heated rectangular cavity flow show that the heat transfer coefficient is insensitive to the Richardson number [9] . Experimental studies on the natural convection in tilted rectangular cavity have been studied [10] and it is found that the heat transfer depends on the angle of heating the top wall. It is found that for 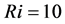 multi-cellular flow is observed which alter the isotherm structure. The instability in the mixed convective flow and heat transfer in a cavity for positive and negative values of Grashof number
multi-cellular flow is observed which alter the isotherm structure. The instability in the mixed convective flow and heat transfer in a cavity for positive and negative values of Grashof number 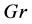 in which top upper wall is heated with constant temperature are studied [11] and it is found that if the aspect ratio of the cavity is equal to 2, a Hopf bifurcation takes place. A numerical study on the mixed convection lid driven flow in a square cavity with cold vertical walls and sinusoidally heated bottom wall show that the strength of circulation increases with
in which top upper wall is heated with constant temperature are studied [11] and it is found that if the aspect ratio of the cavity is equal to 2, a Hopf bifurcation takes place. A numerical study on the mixed convection lid driven flow in a square cavity with cold vertical walls and sinusoidally heated bottom wall show that the strength of circulation increases with 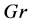 and irrespective of
and irrespective of  and
and  and further that the overall power law correlation for mean
and further that the overall power law correlation for mean 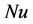 could not be obtained [12] . The effect of different orientation of temperature gradient in the mixed convective heat transfer is studied recently [13] using a finite difference scheme similar to the one in [14] and found that heat transfer rate increases with the decrease of
could not be obtained [12] . The effect of different orientation of temperature gradient in the mixed convective heat transfer is studied recently [13] using a finite difference scheme similar to the one in [14] and found that heat transfer rate increases with the decrease of  which is independent of the orientation of temperature gradient on the adiabatic walls. It is also found that a thermally stratified fluid will result when the top wall is heated and bottom wall is kept cold. A further extension of studies to evaluate the effect of Richardson and Prandtl number is also reported [15] . Essentially, most of the studies in the literature focus on the flow and heat transfer properties due to bottom uniformly and non-uniformly heated surfaces [13] [15] - [25] , studies emerging due to heating of vertical walls [26] - [33] , reports on uniformly heated top wall [34] [35] , and studies employing internal heat sources [36] [37] . A summary of previous studies employing different numerical schemes with various heating configurations is listed in Table 1. In the present work, we undertake a systematic analysis of mixed convection flow and associated heat transfer effects in a flow induced by a non-uniformly heated top lid which is moving uniformly using a high order accurate numerical scheme coupled with multigrid method.
which is independent of the orientation of temperature gradient on the adiabatic walls. It is also found that a thermally stratified fluid will result when the top wall is heated and bottom wall is kept cold. A further extension of studies to evaluate the effect of Richardson and Prandtl number is also reported [15] . Essentially, most of the studies in the literature focus on the flow and heat transfer properties due to bottom uniformly and non-uniformly heated surfaces [13] [15] - [25] , studies emerging due to heating of vertical walls [26] - [33] , reports on uniformly heated top wall [34] [35] , and studies employing internal heat sources [36] [37] . A summary of previous studies employing different numerical schemes with various heating configurations is listed in Table 1. In the present work, we undertake a systematic analysis of mixed convection flow and associated heat transfer effects in a flow induced by a non-uniformly heated top lid which is moving uniformly using a high order accurate numerical scheme coupled with multigrid method.
![]()
Table 1. An overview of previous reports on the lid-driven cavity flows with various types of heating configuration and numerical methods used.
wall.
Abbreviation: MC: Mixed Convection; NC: Natural Convection; LBM: Lattice Boltzmann Method; FVM: Finite Volume Method; FEM: FiniteElement Method; FDM: Finite Difference Method.
2. Modelling and Governing Equations
We consider steady, viscous, incompressible fluid which is completely filled inside a square cavity. The schematic diagram for the flow configuration and the boundary condition applied are depicted in Figure 1. Only the upper lid is allowed to move with a uniform velocity from left to right. The side vertical walls marked with A are thermally adiabatic. The Boussinesq approximation for the fluid is applied so that its density variation together with physical movement of lid leads to non-isothermal laminar mixed convection in cavity. The governing equations are Navier-Stokes equations with buoyancy term coupled with energy equation together with incompressibility condition and are given by
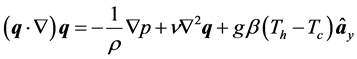 (1)
(1)
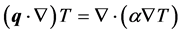 (2)
(2)
![]() (3)
(3)
where ![]() are velocity, pressure and temperature of the fluid respectively. The kinematic viscosity of the fluid is
are velocity, pressure and temperature of the fluid respectively. The kinematic viscosity of the fluid is ![]() and let
and let ![]() be the volumetric coefficient of thermal expansion of the fluid. Let
be the volumetric coefficient of thermal expansion of the fluid. Let ![]() and
and ![]() denote the hot and cold wall temperatures and a be the thermal diffusivity of the fluid. Non-dimensio- nalization is carried out with the following definitions
denote the hot and cold wall temperatures and a be the thermal diffusivity of the fluid. Non-dimensio- nalization is carried out with the following definitions
![]() (4)
(4)
where ![]() denotes physical quantities in dimensional form. Further let the uniform velocity of the top wall be
denotes physical quantities in dimensional form. Further let the uniform velocity of the top wall be![]() . Based on the above scaling parameters, the non-dimensionalized form of the governing equations are
. Based on the above scaling parameters, the non-dimensionalized form of the governing equations are
![]() (5)
(5)
![]() (6)
(6)
![]() (7)
(7)
where ![]() is the unit vector in direction normal to gravitational force and
is the unit vector in direction normal to gravitational force and ![]() denotes the dimensionless temperature of the fluid. The dimensionless parame- ters for the problem are the Reynolds number
denotes the dimensionless temperature of the fluid. The dimensionless parame- ters for the problem are the Reynolds number![]() , the Grashof number
, the Grashof number ![]() and the Prandtl number
and the Prandtl number ![]() and a non-independent parameter Richardson
and a non-independent parameter Richardson
![]()
Figure 1. Schematic diagram of square cavity with vertical adiabatic walls for mixed convective heat transfer simulation.
number![]() . In the stream function-vorticity or y-w formulation, the governing equations become
. In the stream function-vorticity or y-w formulation, the governing equations become
![]() (8)
(8)
![]() (9)
(9)
![]() (10)
(10)
where ![]() is vorticity of the fluid, u and v are defined in terms of streamfunction as
is vorticity of the fluid, u and v are defined in terms of streamfunction as
![]() (11)
(11)
![]() (12)
(12)
![]() (13)
(13)
The boundary conditions used in the present case are as follows. Let the horizontal and vertical components of velocity ![]() be u and v respectively. Only for the top horizontal wall,
be u and v respectively. Only for the top horizontal wall, ![]() and
and ![]() is applied. For all other walls,
is applied. For all other walls,![]() . Also,
. Also, ![]() on all walls. The viscosity of the fluid which is in contact with the surface of the wall generates vorticity
on all walls. The viscosity of the fluid which is in contact with the surface of the wall generates vorticity ![]() in the fluid, which is given by
in the fluid, which is given by ![]() where n refers to a direction perpendicular to the wall. The boundary conditions for temperature is as follows. A linearly varying temperature given by
where n refers to a direction perpendicular to the wall. The boundary conditions for temperature is as follows. A linearly varying temperature given by ![]() is prescribed for the top moving wall while the bottom horizontal wall is held at fixed temperature given by
is prescribed for the top moving wall while the bottom horizontal wall is held at fixed temperature given by![]() . The two vertical walls are held thermodynamically adiabatic which means no heat flux can enter or leave the wall and therefore we have
. The two vertical walls are held thermodynamically adiabatic which means no heat flux can enter or leave the wall and therefore we have ![]() on the vertical walls. Here
on the vertical walls. Here ![]() refers to a direction normal to the surface of the wall.
refers to a direction normal to the surface of the wall.
3. Discretization Scheme
Here, we describe the discretization procedure for to the governing set of partial differential equations. Let h and k denotes the grid spacing ![]() then, from Taylor series expansion, we have, the fourth order accurate finite difference representation for the first and second derivatives as follows.
then, from Taylor series expansion, we have, the fourth order accurate finite difference representation for the first and second derivatives as follows.
![]() (14)
(14)
![]() (15)
(15)
![]() (16)
(16)
![]() (17)
(17)
where![]() ,
, ![]() ,
, ![]() and
and ![]() are second order central difference operators which are given by
are second order central difference operators which are given by
![]() (18)
(18)
![]() (19)
(19)
![]() (20)
(20)
![]() (21)
(21)
Similarly, the higher order cross derivative operators can be written as
![]() (22)
(22)
![]() (23)
(23)
![]() (24)
(24)
![]() (25)
(25)
3.1. Discretization of Streamfunction Equation
Substituting (15) and (17) in the streamfunction Equation (8) and using the ![]() -operator from Equations (18) to (25) we get finite difference representation of streamfunction equation as given below
-operator from Equations (18) to (25) we get finite difference representation of streamfunction equation as given below
![]() (26)
(26)
with the truncation error ![]() in the above equation is given by
in the above equation is given by
![]() (27)
(27)
Now, to eliminate higher derivatives of ![]() in the truncation error term, we differentiate Equation (8) once and twice with respect to x and y respectively to yield the following.
in the truncation error term, we differentiate Equation (8) once and twice with respect to x and y respectively to yield the following.
![]() (28)
(28)
![]() (29)
(29)
![]() (30)
(30)
![]() (31)
(31)
First we substitute (29) and (31) in (27) and then all the derivatives are replaced by suitable expressions from the set of Equations (18) to (25). The resulting simplified expression for ![]() is substituted in (26) and rearranged so that we obtain the fourth order accurate discretized form of streamfunction Equation (8) as given below.
is substituted in (26) and rearranged so that we obtain the fourth order accurate discretized form of streamfunction Equation (8) as given below.
![]() (32)
(32)
where the constants in the above equations are
![]() (33)
(33)
![]() (34)
(34)
![]() (35)
(35)
and ![]() represents the 8 nearest neighboring points together with a center
represents the 8 nearest neighboring points together with a center
point on the computational domain.
3.2. Discretization of Vorticity Equation
Now, the vorticity Equation (9) is rewritten as
![]() (36)
(36)
and the associated coefficients are
![]() (37)
(37)
![]() (38)
(38)
![]() (39)
(39)
Next, the Equation (36) is written in terms of finite difference operator notation and which is valid for the grid point![]() . Accordingly, the coefficients c, d and q will have the suffix of the grid point under consideration as given below.
. Accordingly, the coefficients c, d and q will have the suffix of the grid point under consideration as given below.
![]() (40)
(40)
with a truncation error ![]() given by
given by
![]() (41)
(41)
To eliminate the derivatives appearing in the truncation error term (41), we differentiate the vorticity Equation (36) to yield the following set of expressions
![]() (42)
(42)
![]() (43)
(43)
![]() (44)
(44)
![]() (45)
(45)
First we insert (42) to (45) in the truncation error term (41) and then substitute the resulting expression for ![]() in (40) and then apply D-operators from (18) to (25) so that we will get
in (40) and then apply D-operators from (18) to (25) so that we will get
![]() (46)
(46)
The coefficients in the above equation are,
![]() (47)
(47)
![]() (48)
(48)
![]() (49)
(49)
![]() (50)
(50)
![]() (51)
(51)
Upon simplifying the above Equation (46), we will get the fourth order accurate finite difference representation of the vorticity differential Equation (36) as given below.
![]() (52)
(52)
It may be noted that before implementing the code for Equation (10), the expressions for the quantities c, d and q should also be replaced by fourth order accurate relations as given below.
![]() (53)
(53)
![]() (54)
(54)
![]() (55)
(55)
3.3. Discretization of Energy Equation
Now, the temperature Equation (10) is rewritten as
![]() (56)
(56)
Let us define primed variables ![]() and
and ![]() at the grid point
at the grid point ![]() as
as
![]() (57)
(57)
![]() (58)
(58)
Using Equations (14) to (17) together with the above two primed variables in (10), we get discretized version with truncation error term as follows.
![]() (59)
(59)
and the truncation error term ![]() in the previous equation is
in the previous equation is
![]() (60)
(60)
Now the higher order derivatives of T present in the previous expression for truncation error can be eliminated by differentiating the energy Equation (10) with respect to x and y to yield the following.
![]() (61)
(61)
![]() (62)
(62)
![]() (63)
(63)
![]() (64)
(64)
Substituting the set of Equations (61) to (64) in the equation for truncation error (60) and also applying the D operators from (18) to (25), in the Equation (59) we get
![]() (65)
(65)
where the coefficients![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() appearing in the above equation are
appearing in the above equation are
![]() (66)
(66)
![]() (67)
(67)
![]() (68)
(68)
![]() (69)
(69)
![]() (70)
(70)
It may be noted that before implementing the code for Equation (65), the expressions for primed quantities ![]() and
and ![]() should also be replaced by fourth order accurate relations as given below.
should also be replaced by fourth order accurate relations as given below.
![]() (71)
(71)
![]() (72)
(72)
and the constants![]() ,
, ![]() and
and ![]() are already defined in Equations (33) to (35). Finally, we have arrived at a set of three coupled discretized Equations (32), (52) and (65) whose accuracy is
are already defined in Equations (33) to (35). Finally, we have arrived at a set of three coupled discretized Equations (32), (52) and (65) whose accuracy is![]() .
.
4. Implementation of Numerical Scheme
The set of coupled discretized equations as mentioned above is applied to each grid point in the computational domain and this produces a large linear sparse system which exhibits diagonal dominance. Therefore we could use the multigrid method with Gauss-Seidel iteration as relaxer. We have chosen to use the multigrid method because it accelerates convergence when compared to using stand-alone iterative procedures. The set of grids used are![]() ,
, ![]() ,
, ![]() ,
, ![]() and
and![]() . If the solution
. If the solution ![]() of a particular equation in the finest grid
of a particular equation in the finest grid ![]() is denoted by
is denoted by ![]() then the solution of the same equation in the next finer grid
then the solution of the same equation in the next finer grid ![]() will be denoted by
will be denoted by![]() . We have used the simplest of the restriction operator, called the injection operator
. We have used the simplest of the restriction operator, called the injection operator ![]() which simply copies the finest grid solution to the next finer grid (or the coarsest grid as the case may be) at grid points which are common to both grid levels. In Figure 2, the stars denote boundary points and the circles are points that are common to two different grids. The injection operation involves equating the values at circles in
which simply copies the finest grid solution to the next finer grid (or the coarsest grid as the case may be) at grid points which are common to both grid levels. In Figure 2, the stars denote boundary points and the circles are points that are common to two different grids. The injection operation involves equating the values at circles in ![]() grid to the circles in
grid to the circles in ![]() grid (Figure 2). The reverse operation to injection is known as prolongation operation
grid (Figure 2). The reverse operation to injection is known as prolongation operation![]() . The prolongation operation is done for the points shown as square in Figure 2 as follows. The value of
. The prolongation operation is done for the points shown as square in Figure 2 as follows. The value of ![]() at grid point
at grid point ![]() in
in ![]() grid is equal to the value of
grid is equal to the value of ![]() at
at ![]() in
in ![]() grid, which is written as,
grid, which is written as,
![]() (73)
(73)
In general, if the finest grid is represented as ![]() and the next finer grid is represented as
and the next finer grid is represented as ![]() then the above equation is rewritten as,
then the above equation is rewritten as,
![]() (74)
(74)
The value of ![]() in
in ![]() grid at point
grid at point ![]() grid is equal to the average of values of
grid is equal to the average of values of ![]() at
at ![]() and
and ![]() in
in ![]() grid. This is expressed in general as
grid. This is expressed in general as
![]() (75)
(75)
![]()
![]()
Figure 2. Schematic of two-level grids used for illustrating the injection and prolongation operations. Circles are points common to both grids. Stars are boundary (or known) points. The squares are the points at which the value is to be found using the prolonga- tion operation.
Here ![]() means finest grid and
means finest grid and ![]() means next finer (or coarsest) grid. Similarly, the values at all other square points are obtained using the following averaging scheme.
means next finer (or coarsest) grid. Similarly, the values at all other square points are obtained using the following averaging scheme.
![]() (76)
(76)
![]() (77)
(77)
The above set of Equations (74) to (77) comprise the 9-point prolongation operator [38] . The three coupled discretized Equations (32), (52) and (65) are relaxed simultaneously and the boundary conditions are incorporated implicitly. A point Gauss-Seidel iterative scheme is used for the relaxation procedure. This pre-smoothing iterations are carried out on the finest grid. Then we restrict (or inject) the residual on the coarsest grid. Let the residual be denoted by![]() . By solving the matrix equation
. By solving the matrix equation ![]() we get the error in the coarsest grid. This error
we get the error in the coarsest grid. This error ![]() is prolongated to the finest grid and then added to
is prolongated to the finest grid and then added to ![]() as below
as below
![]() (78)
(78)
where ![]() is the prolongation operator (for more details, see [38] ). After performing a few post-smoothing operation, one multigrid cycle is completed. This procedure is repeated until the following condition is satisfied for convergence.
is the prolongation operator (for more details, see [38] ). After performing a few post-smoothing operation, one multigrid cycle is completed. This procedure is repeated until the following condition is satisfied for convergence.
![]() (79)
(79)
where ![]() is any of
is any of ![]() and
and ![]() is the iteration number.
is the iteration number.
Treatment of Boundary Points
At all the boundary points, fourth order accurate one sided finite-difference formula is used for derivatives involving ![]() and
and![]() . The first derivative of temperature along all points in left vertical wall is
. The first derivative of temperature along all points in left vertical wall is
![]() (80)
(80)
and similarly the same for the right vertical wall is expressed as
![]() (81)
(81)
A fourth order backward difference scheme is used to find ![]() at top moving wall.
at top moving wall.
![]() (82)
(82)
Similarly, the fourth order one sided finite difference is used to find ![]() at all other walls
at all other walls
![]() (83)
(83)
![]() (84)
(84)
![]() (85)
(85)
5. Results and Discussion
The flow characteristics together with thermal fields are computed for different![]() ,
, ![]() and
and ![]() (or equivalent
(or equivalent![]() ). The density variation is induced through a linearly varying top moving wall. The effect of mixed convection is analyzed through streamlines, isothermal contours and Nusselt number for
). The density variation is induced through a linearly varying top moving wall. The effect of mixed convection is analyzed through streamlines, isothermal contours and Nusselt number for![]() ,
, ![]() and Grashof number
and Grashof number ![]() and further explained through contours of components of velocity and temperature in the mid-cross-section of the cavity. At the end, the numerical accuracy of the proposed scheme is established.
and further explained through contours of components of velocity and temperature in the mid-cross-section of the cavity. At the end, the numerical accuracy of the proposed scheme is established.
5.1. Code Validation and Grid Independence Study
To validate our coding we have run the program with aiding and opposing shear boundary conditions available in the literature. The validations are done for various values of ![]() and a fixed value of
and a fixed value of![]() . The parameter used to study the mixed convection is Richardson number
. The parameter used to study the mixed convection is Richardson number ![]() which is also equal to
which is also equal to![]() . The case of
. The case of ![]() belongs to the class of forced convection and if
belongs to the class of forced convection and if ![]() we may describe as mixed convection. Table 2 shows the grid independence results for
we may describe as mixed convection. Table 2 shows the grid independence results for ![]() case in terms of values of streamfunction,
case in terms of values of streamfunction, ![]() , and vorticity,
, and vorticity, ![]() which are evaluated at the centers of primary and two secondary vortices for different values of
which are evaluated at the centers of primary and two secondary vortices for different values of![]() . Here a fluid with a constant
. Here a fluid with a constant ![]() is considered. In our computation, the coarser grids are
is considered. In our computation, the coarser grids are![]() ,
, ![]() , and
, and ![]() while the finest grid used in the present study is
while the finest grid used in the present study is![]() . From the tabulated data, it is seen that
. From the tabulated data, it is seen that ![]() grid is found to be optimum. Further refining of grids will not give more accuracy because the accuracy of the numerical scheme is decided by method of discretization and not by the fineness of the grid. The advantage with the present higher order scheme is that we can achieve the accurate results in smaller grid itself. Table 3 shows the location of primary vortex and flow parameters such as streamfunction and vorticity in different grids, and they are compared with the literature data that include data that might have been computed using a lower order finite difference method [1] [13] [14] [39] [40] [41] , and from the tabulated data it is observed that there is a very good agreement among different reports. In particular, the results of [14] is matching to a good degree with that of our computed value. In
grid is found to be optimum. Further refining of grids will not give more accuracy because the accuracy of the numerical scheme is decided by method of discretization and not by the fineness of the grid. The advantage with the present higher order scheme is that we can achieve the accurate results in smaller grid itself. Table 3 shows the location of primary vortex and flow parameters such as streamfunction and vorticity in different grids, and they are compared with the literature data that include data that might have been computed using a lower order finite difference method [1] [13] [14] [39] [40] [41] , and from the tabulated data it is observed that there is a very good agreement among different reports. In particular, the results of [14] is matching to a good degree with that of our computed value. In
![]()
Table 2. The grid independence study of in terms of stream function and vorticity at the centres of primary and secondary vortices located at bottom left (BL) and bottom right (BR) respectively.
![]()
Table 3. Comparison of computed values of streamfunction, vorticity and coordinates (x, y) of primary vortex with literature.
order to perform validation for heat transfer studies, we have exclusively run the code with the boundary condition ![]() for the top moving wall and the results are shown in Table 4 and the data is compared with literature [15] [42] [43] . Essentially there is hardly a 0.03% variation among other reported values that has been computed using some fourth order scheme and 0.1% variation among second order accurate computations.
for the top moving wall and the results are shown in Table 4 and the data is compared with literature [15] [42] [43] . Essentially there is hardly a 0.03% variation among other reported values that has been computed using some fourth order scheme and 0.1% variation among second order accurate computations.
5.2. Flow Structure and Isotherms
Experimental investigation of lid-driven flow and its effect on density variations show that [44] [45] the flow consists mainly of a central recirculating zone with one downstream secondary eddy (DSE) and one upstream secondary eddy (USE). Additional secondary eddy may be formed if the Reynolds number is suitably high (Figure 3). Experimentally it is also known that if the ![]() the flow first becomes three-dimensional and later leads to turbulent cavity flow. Starting with low
the flow first becomes three-dimensional and later leads to turbulent cavity flow. Starting with low ![]() case, a fluid with
case, a fluid with ![]() is taken and the Figure 3 shows streamlines and temperature isotherms for increasing buoyancy with
is taken and the Figure 3 shows streamlines and temperature isotherms for increasing buoyancy with![]() , 104 and 105 respectively from top to bottom. The dashed lines in the streamlines correspond to flow in clockwise direction while the anticlockwise flow is shown as solid lines. In the present configuration, both shear stress and density variation are created near the upper moving lid because the bottom lid is held at a lower constant temperature and the side vertical walls are thermally insulated. This cavity flow configuration is in contrast with other studies reported in the literature [15] [46] . Other notable studies where the bottom wall is colder than the top moving lid are [42] [47] but however, the vertical walls are not necessarily held adiabatic. The top plot in Figure 4 correspond to negligible
, 104 and 105 respectively from top to bottom. The dashed lines in the streamlines correspond to flow in clockwise direction while the anticlockwise flow is shown as solid lines. In the present configuration, both shear stress and density variation are created near the upper moving lid because the bottom lid is held at a lower constant temperature and the side vertical walls are thermally insulated. This cavity flow configuration is in contrast with other studies reported in the literature [15] [46] . Other notable studies where the bottom wall is colder than the top moving lid are [42] [47] but however, the vertical walls are not necessarily held adiabatic. The top plot in Figure 4 correspond to negligible
![]()
Table 4. Comparison of average Nusselt number Nm in the top moving wall where the boundary condition imposed is T = 1 for the fluid flow with Pr = 0.73.
![]()
Figure 3. Schematic of streamlines with possibble recirculation regions. PV is the primary vortex, USE is upstream secondary eddy, DSE is the downstream secondary eddy and TSE is the top left secondary eddy.
buoyant force ![]() and the flow is due mainly to the shear force provided by moving lid and hence we compare the positions of primary and additional eddies against the literature [48] .
and the flow is due mainly to the shear force provided by moving lid and hence we compare the positions of primary and additional eddies against the literature [48] .
From the isotherm contours of Figure 4, (right side plots) it is observed that the temperature of the fluid in the cavity for ![]() case has non-uniform layered structure and this has resulted due predominantly to forced convection effects. If we come to the mixed convection region
case has non-uniform layered structure and this has resulted due predominantly to forced convection effects. If we come to the mixed convection region![]() , a considerable change in both flow structure and thermal fields can be seen (middle and bottom plots of Figure 4). For
, a considerable change in both flow structure and thermal fields can be seen (middle and bottom plots of Figure 4). For ![]() case, the thermal boundary layer thickness with respect to bottom wall increases as
case, the thermal boundary layer thickness with respect to bottom wall increases as ![]() increases. As the increase of buoyant force by increasing
increases. As the increase of buoyant force by increasing![]() , the size of the secondary BR (bottom right) vortex decreases. Simultaneously the BL (bottom left) secondary vortex increases so as to form two analogous large counter rotating vortices that occupies the entire cavity. Table 5 shows the growth, merging and mixing of secondary vortices with the increase of Grashof number for different values of
, the size of the secondary BR (bottom right) vortex decreases. Simultaneously the BL (bottom left) secondary vortex increases so as to form two analogous large counter rotating vortices that occupies the entire cavity. Table 5 shows the growth, merging and mixing of secondary vortices with the increase of Grashof number for different values of![]() . From the table it is noted that the USE and DSE are merges for Richardson number
. From the table it is noted that the USE and DSE are merges for Richardson number![]() . Even though the flow structure changes dramatically, the temperature distribution in the layers of the fluid have nearly a flat or uniform thermal gradient. This is in contrast to thermal distribution for low
. Even though the flow structure changes dramatically, the temperature distribution in the layers of the fluid have nearly a flat or uniform thermal gradient. This is in contrast to thermal distribution for low ![]() case where large amount of fluid is nearly isothermal. When the Richardson number is significant, that is, when mixed convection plays a role, the size of the USE on bottom left corner increases at the expense of DSE which is located on the bottom right side of the cavity. This could be due to the suppression of adverse pressure gradient which in turn is due to the thermal gradient existing between top and bottom walls.
case where large amount of fluid is nearly isothermal. When the Richardson number is significant, that is, when mixed convection plays a role, the size of the USE on bottom left corner increases at the expense of DSE which is located on the bottom right side of the cavity. This could be due to the suppression of adverse pressure gradient which in turn is due to the thermal gradient existing between top and bottom walls.
![]()
Table 5. Growth, degradation and merging of secondary vortices due to increased mixed convection.
When Richardson number is increased to![]() , a significant change in the fluid flow is observed, wherein the USE grows until it occupies nearly half of the cavity, which is attributed to the buoyancy effects. The direction of flow in this eddy is opposite to that of the main or primary vortex. In addition, the center of primary vortex moves towards the right wall as
, a significant change in the fluid flow is observed, wherein the USE grows until it occupies nearly half of the cavity, which is attributed to the buoyancy effects. The direction of flow in this eddy is opposite to that of the main or primary vortex. In addition, the center of primary vortex moves towards the right wall as ![]() increases. The size of the clockwise and anticlockwise rotating vortices have same size, which shows that the effect of shear driven forced convection effect and buoyancy driven convection effects shows equal strength. The thermal contours have more shift than
increases. The size of the clockwise and anticlockwise rotating vortices have same size, which shows that the effect of shear driven forced convection effect and buoyancy driven convection effects shows equal strength. The thermal contours have more shift than ![]() case of Figure 4, towards the top lid. The thermal stratification of fluid is visible for
case of Figure 4, towards the top lid. The thermal stratification of fluid is visible for ![]() case than the other two cases (
case than the other two cases (![]() and
and![]() ). In this range the conduction effect of fluid also plays a vital role. Most of the heat transfer occurring near the stratified fluid is due to conduction, whereas the convection is dominant near the top sliding wall. While considering the recirculation at the middle and bottom of the cavity, the streamlines are more than two- order of magnitude smaller than top sliding wall, which shows the fluid is almost stagnant in the stratified fluid towards the bottom region. The streamlines and isotherms for
). In this range the conduction effect of fluid also plays a vital role. Most of the heat transfer occurring near the stratified fluid is due to conduction, whereas the convection is dominant near the top sliding wall. While considering the recirculation at the middle and bottom of the cavity, the streamlines are more than two- order of magnitude smaller than top sliding wall, which shows the fluid is almost stagnant in the stratified fluid towards the bottom region. The streamlines and isotherms for ![]() is plotted in Figure 5. When
is plotted in Figure 5. When ![]() is increased to 400, the corresponding growth of secondary vortices are observed. The middle plot of Figure 5 shows a growth of secondary upstream vortex and degradation of secondary downstream vortex is observed. Also, a small shift in the position of primary vortex towards the downstream flow region is noticed. The isotherms for weak mixed convection (
is increased to 400, the corresponding growth of secondary vortices are observed. The middle plot of Figure 5 shows a growth of secondary upstream vortex and degradation of secondary downstream vortex is observed. Also, a small shift in the position of primary vortex towards the downstream flow region is noticed. The isotherms for weak mixed convection (![]() ) show that the heat transfer in a more-or-less uniform layered structure till it reaches the center of primary vortex. If
) show that the heat transfer in a more-or-less uniform layered structure till it reaches the center of primary vortex. If ![]() is increased by ten times, to
is increased by ten times, to![]() , the thermal gradients are reduced but still the isotherm structure is retained. For strong convection case of
, the thermal gradients are reduced but still the isotherm structure is retained. For strong convection case of![]() , it is observed that the sudden growth of upstream secondary vortex due to the increase of unfavorable pressure gradient and the complete suppression of downstream secondary vortex due to the decrease of shear force by the increase of temperature in the downstream makes a favorable pressure gradient. Interestingly a clockwise small vortex forms on the apex of vertical wall near the lid in the downstream region. This is due to the formation of stagnant pressure by the friction loss in the primary vortex itself. Also noted that primary vortex shifts towards the bottom region of the cavity. The temperature distribution is more towards the bottom surface of the cavity. Stagnant layers of fluids is visible in the upstream region. The similar effect is observed for
, it is observed that the sudden growth of upstream secondary vortex due to the increase of unfavorable pressure gradient and the complete suppression of downstream secondary vortex due to the decrease of shear force by the increase of temperature in the downstream makes a favorable pressure gradient. Interestingly a clockwise small vortex forms on the apex of vertical wall near the lid in the downstream region. This is due to the formation of stagnant pressure by the friction loss in the primary vortex itself. Also noted that primary vortex shifts towards the bottom region of the cavity. The temperature distribution is more towards the bottom surface of the cavity. Stagnant layers of fluids is visible in the upstream region. The similar effect is observed for![]() , where a clockwise vortex formed in the downstream vertical wall and stationary bottom surface Figure 6 (bottom plot). The changes are insignificant for higher
, where a clockwise vortex formed in the downstream vertical wall and stationary bottom surface Figure 6 (bottom plot). The changes are insignificant for higher ![]() for all values of
for all values of ![]() with the fixed case of
with the fixed case of ![]() Figure 7. The clustered temperature isotherms near the top and bottom walls indicates that an large change in the gradient of temperature with respect to normal to the direction of the surface. Whereas the temperature in the recirculation region, the clustering of contours are weak. Hence the temperature gradient is very small indicating that hot fluid is mixed with the cold fluid in that region. In the case of
Figure 7. The clustered temperature isotherms near the top and bottom walls indicates that an large change in the gradient of temperature with respect to normal to the direction of the surface. Whereas the temperature in the recirculation region, the clustering of contours are weak. Hence the temperature gradient is very small indicating that hot fluid is mixed with the cold fluid in that region. In the case of![]() , the velocity of the fluid is high, hence the mixing of fluid due to
, the velocity of the fluid is high, hence the mixing of fluid due to
shear effect is more significant than buoyancy effect.
The influence of ![]() in flow dynamics and heat transfer is shown in the Figure 8. The flow features inside the cavity remains almost unaltered while increasing the Prandtl number for the forced convective heat transfer (
in flow dynamics and heat transfer is shown in the Figure 8. The flow features inside the cavity remains almost unaltered while increasing the Prandtl number for the forced convective heat transfer (![]() ). From the figure, the position and the size of primary and secondary vortices are unaltered with the increase of
). From the figure, the position and the size of primary and secondary vortices are unaltered with the increase of![]() , which indicates that flow dynamics is independent of
, which indicates that flow dynamics is independent of ![]() due to the absence of buoyancy force on the flow for low range of Richardson numbers. The temperature distribution inside the cavity is shown on the right side of the Figure 8 and show that heat transfer properties are significantly changes with
due to the absence of buoyancy force on the flow for low range of Richardson numbers. The temperature distribution inside the cavity is shown on the right side of the Figure 8 and show that heat transfer properties are significantly changes with![]() . The thermal boundary layer thickness on bottom and top surface of the cavity (at very low
. The thermal boundary layer thickness on bottom and top surface of the cavity (at very low![]() ) develops in a layered structure in a stratified manner. While increasing
) develops in a layered structure in a stratified manner. While increasing![]() , the temperature isotherms show that heat transfer extends to the entire region of the cavity together with a thinning
, the temperature isotherms show that heat transfer extends to the entire region of the cavity together with a thinning
effect of thermal boundary layer on the top and bottom surface of the cavity. The numerical experiments are carried out with the increase of ![]() from 104 to 106 which is shown in Figure 9 and a significant change of flow and heat transfer is observed due to large buoyancy force. For small values of
from 104 to 106 which is shown in Figure 9 and a significant change of flow and heat transfer is observed due to large buoyancy force. For small values of ![]() the effect is same as that of Figure 8. While increasing Prandtl number, the downstream secondary eddy degrades and the upstream secondary eddy enlarges. Due to linear heating of top wall, maximum heat on the left portion of lid (
the effect is same as that of Figure 8. While increasing Prandtl number, the downstream secondary eddy degrades and the upstream secondary eddy enlarges. Due to linear heating of top wall, maximum heat on the left portion of lid (![]() ) moves towards the downstream region of the cavity and hence the USE grows. At the same time buoyancy opposes the primary core flow and affects the upstream boundary layer to detach from the wall. For high
) moves towards the downstream region of the cavity and hence the USE grows. At the same time buoyancy opposes the primary core flow and affects the upstream boundary layer to detach from the wall. For high ![]() flows, clockwise recirculation zone is formed on the left wall. For
flows, clockwise recirculation zone is formed on the left wall. For![]() , the heat transfer in the cavity is due to conduction, shows a thick boundary layer all over the cavity resulting a mild change of temperature produces a feeble buoyant force. For
, the heat transfer in the cavity is due to conduction, shows a thick boundary layer all over the cavity resulting a mild change of temperature produces a feeble buoyant force. For![]() , the
, the
heat transfer is mainly due to convective effect and the fluid is well mixed in the core of the cavity, hence the buoyant effect exhibits near the walls of the cavity. This makes the degradation of downstream eddy and upgradation of upstream secondary vortex. The reverse will happens for a gravitationally unstable condition [46] , where they observed the degradation of upstream secondary vortex and growth of downstream secondary vortex.
Contours of the horizontal and vertical components of velocity u and v are plotted in Figure 10 and Figure 11 for ![]() and 1000 respectively. In the case of
and 1000 respectively. In the case of ![]() (Figure 10), we could see that the vertical components of velocity V is modified to a great extent in the left half of the cavity because of the nature of buoyancy which is
(Figure 10), we could see that the vertical components of velocity V is modified to a great extent in the left half of the cavity because of the nature of buoyancy which is ![]() in our case. Consequently, the density variations are more in left half and they are least in the right half of the cavity. This leads a way to develop two large circulations in opposite directions as seen in
in our case. Consequently, the density variations are more in left half and they are least in the right half of the cavity. This leads a way to develop two large circulations in opposite directions as seen in
bottom left of Figure 4. For the case of ![]() (Figure 11) however, the minimal viscous force causes the formation of multiple recirculation region. It is also noted that, both velocity components are responsible for the emergence of corner vortices. While increasing
(Figure 11) however, the minimal viscous force causes the formation of multiple recirculation region. It is also noted that, both velocity components are responsible for the emergence of corner vortices. While increasing ![]() the growth of secondary vortices are visible to both velocity components, this effects are due to the conventional flows in a lid-driven cavity. Also the contour lines are pushed towards the top region of the cavity. Due to the push of buoyant force against the gravity, USE grows and finally it form a separate cell near the bottom region of the cavity in the horizontal velocity component, which is visible in the Figure 11 (bottom left). It is also noted that the horizontal components of velocity undergoes changes as high as three orders of magnitude within the cavity.
the growth of secondary vortices are visible to both velocity components, this effects are due to the conventional flows in a lid-driven cavity. Also the contour lines are pushed towards the top region of the cavity. Due to the push of buoyant force against the gravity, USE grows and finally it form a separate cell near the bottom region of the cavity in the horizontal velocity component, which is visible in the Figure 11 (bottom left). It is also noted that the horizontal components of velocity undergoes changes as high as three orders of magnitude within the cavity.
Cross sectional profiles of velocity and temperature Figure 12 shows the vertical (v) and horizontal (u) components of velocities along the x and y directions
along vertical center line and horizontal mid-heights respectively. The dash-dot lines of Figure 12 show the flow in forced convective range. In this case, the velocity is maximum near the walls and the fluid is stagnant in center region of the cavity. This is the expected behavior of lid-driven cavity flow in the absence of buoyant force. In other cases, the velocity changes considerably. Figure 13 shows the variation of velocity with ![]() (top plot) and
(top plot) and ![]() (bottom plot) respectively. From the top plot it is clear that while increasing buoyancy effect the fluid tends to degrade the shear action by moving the line closely towards the stagnant line. Prandtl number have vital effect to pull the fluid to stagnant which is visible from the bottom plot. Figure 14 shows the temperature profile along vertical and horizontal directions at horizontal mid-length and vertical mid- height for different values of
(bottom plot) respectively. From the top plot it is clear that while increasing buoyancy effect the fluid tends to degrade the shear action by moving the line closely towards the stagnant line. Prandtl number have vital effect to pull the fluid to stagnant which is visible from the bottom plot. Figure 14 shows the temperature profile along vertical and horizontal directions at horizontal mid-length and vertical mid- height for different values of ![]() and
and ![]() respectively. All curves shows
respectively. All curves shows
minimum temperature at bottom wall and maximum at top wall. In the case of ![]() (continuous line plot), for a fixed
(continuous line plot), for a fixed![]() , temperature distribution shows a linear variation along vertical direction due to the fact that the fluid inside the cavity is almost stagnant which is seen in the Figure 14 (top left,
, temperature distribution shows a linear variation along vertical direction due to the fact that the fluid inside the cavity is almost stagnant which is seen in the Figure 14 (top left,![]() ). Hence the gradient of temperature is pronounced. Same variation is observed along the horizontal direction Figure 14 (top right,
). Hence the gradient of temperature is pronounced. Same variation is observed along the horizontal direction Figure 14 (top right,![]() ). In the shear force dominated case
). In the shear force dominated case![]() , the temperature variation is significant only very near to the walls, where the conductive heat transfer is dominant and in the middle portion of the cavity, temperature change is insignificant due to the recirculation of fluid, where the convective heat transfer is dominant. The bottom plots in the same Figure 14 shows the case of different Grashof number (
, the temperature variation is significant only very near to the walls, where the conductive heat transfer is dominant and in the middle portion of the cavity, temperature change is insignificant due to the recirculation of fluid, where the convective heat transfer is dominant. The bottom plots in the same Figure 14 shows the case of different Grashof number (![]() ). In this case the horizontal variation of temperature is more signifi-
). In this case the horizontal variation of temperature is more signifi-
cant than the variation along the vertical direction. Figure 15 shows the variation of temperature with ![]() (top plot) and
(top plot) and ![]() (bottom plot) respectively. In this figure, the dash-dash line overlapping with the black continuous line which shows an insignificant change for the values of
(bottom plot) respectively. In this figure, the dash-dash line overlapping with the black continuous line which shows an insignificant change for the values of ![]() and
and![]() . For
. For ![]() it is observed that when
it is observed that when![]() , no significant changes in temperature takes place. However when
, no significant changes in temperature takes place. However when ![]() the temperature along the vertical line of the cavity reduces considerably. For a fixed
the temperature along the vertical line of the cavity reduces considerably. For a fixed ![]() and
and![]() , for very low values of
, for very low values of![]() , the temperature uniformly rises along the vertical distance and changes only slightly along the horizontal center of the cavity. However, if
, the temperature uniformly rises along the vertical distance and changes only slightly along the horizontal center of the cavity. However, if ![]() the temperature remains nearly constant in the middle of the cavity. For
the temperature remains nearly constant in the middle of the cavity. For![]() , a non-monotonic increase in T is noted, both along vertical and horizontal center region.
, a non-monotonic increase in T is noted, both along vertical and horizontal center region.
![]()
Figure 15. Temperature profiles along vertical and horizontal centers of the cavity for different ![]() (top) and for different
(top) and for different ![]() (bottom).
(bottom).
6. Estimation of Order of Accuracy
We have checked the order of accuracy from the computed numerical values using the method of divided difference. In order to evaluate the accuracy of the obtained numerical results, we have taken the center point left corner (formed on the apex of vertical upstream wall and bottom surface) vortex (![]() ) values for
) values for![]() ,
, ![]() with all values of
with all values of ![]() having different grids of step size h. The reason for choosing the centre of vortex is the point where velocity of the fluid is nearly null (
having different grids of step size h. The reason for choosing the centre of vortex is the point where velocity of the fluid is nearly null (![]() is a constant), hence the singularity affected by the velocity vector due to corner vortices are avoided which is explained by Iwatsu et al., [42] . The divided difference with respect to h is calculated as
is a constant), hence the singularity affected by the velocity vector due to corner vortices are avoided which is explained by Iwatsu et al., [42] . The divided difference with respect to h is calculated as
![]() (86)
(86)
A plot between y and the grid step size h is made on a log-log scale which is shown in Figure 16. The four points in the figure correspond to the values obtained in five different grids. It is found that result follow a straight line behaviour with a slope equal to 3. This is true for the flow with any ![]() and
and ![]() considered in this study. Since the quantity in y-axis itself is equivalent to one slope, the overall slope should be 4, indicating that the numerical results obtained will be having fourth order accuracy.
considered in this study. Since the quantity in y-axis itself is equivalent to one slope, the overall slope should be 4, indicating that the numerical results obtained will be having fourth order accuracy.
7. Conclusion
The fourth order compact finite difference scheme is successfully implemented
To study the mixed convection in a lid driven cavity flow with linearly heated top wall. The multigrid iterative procedure allowed a fast convergence to the exact solution. The effect of heat transfer is affected by all the governing parameters as well as the effect of linear heating. The growth and the degradation of USE and DSE are observed for the increase of Richardson number, which shows a significant effect of ![]() over heat transfer. In the mixed convection range, the USE and DSE are merging. The velocity contour shows that, both velocity components are responsible for the emergence of corner vortices. For
over heat transfer. In the mixed convection range, the USE and DSE are merging. The velocity contour shows that, both velocity components are responsible for the emergence of corner vortices. For![]() , a push of buoyant force against the gravity occurs and hence the USE grows and finally it forms a separate cell near the bottom region of the cavity in the horizontal velocity component. The order of accuracy of the derived numerical scheme is found to be four.
, a push of buoyant force against the gravity occurs and hence the USE grows and finally it forms a separate cell near the bottom region of the cavity in the horizontal velocity component. The order of accuracy of the derived numerical scheme is found to be four.
Acknowledgements
One of the authors (R. Sivakumar) would like to thank the UGC for supporting this research work through major project grant vide UGC project grant letter F. No. 37-312/2009 (SR) dated January 12, 2010, and also DST for infrastructure development funds through FIST program vide order SR/FST/PSII-021/2009 dated August 13, 2010. A. D. Abin. Rejeesh acknowledges the DST-INSPIRE fellowship vide DST/INSPIRE/Fellowship/2011/361 order dated August 01, 2013 and finally S. Udhayakumar acknowledges Pondicherry University for providing scholarship.