1. Introduction
This paper describes an advanced solution for the mission of complexity, which was published previously in [1] and [2] . It is an innovative great achievement in modern science and is applicable to multidisciplinary science, such as economics, ecology, and the other sciences. Nevertheless, the advanced solution is solved by the other science such as the principle of systems analysis methods; it is too difficult to study for scientists. Moreover, it is entirely different from the established older solution as the “Chaos Theory” in statistical physics; it is imperfect and incomplete in terms of scientific research; but it has good possibility and capability.
To address this issue, this paper has been described in the following steps [hypothesis]-[experimentation]-[verification], and should be read without any preconceptions. We have organized this paper in the following steps. 1) We clarify the academic reasoning and relevant scientific background behind solution. 2) We provide demonstration of the advanced solution using formal scientific program MATLAB or specially designed analog-type simulator, and 3) we consider the paradoxical problem concerned with the Santa Fe Institute (SFI) [3] . Hence, a new solution is established, proving that complexity is a solvable problem with simulation.
2. Hypothesis: Scientific Background of the Advanced Solution
2.1. Scientific Background of the Advanced Solution
It is necessary to clarify the academic reasoning and scientific background behind the new solution to the readers. To this end, we present our premise as a question:
(Question): Do you know the reason why we cannot perform an experiment on complex systems under “real circumstances”? For example, experimental studies on thermal systems in physics, stock market systems in economics, and ecological systems in ecology. The answer is as follows; nobody can interrupt the process of complex systems and fix their activity by human work. Hence, nobody has succeeded in these experiments from the time of the Greek philosopher Aristotle and strangely, no one knows the reason, therefore, it is important to consider the scientific background and academic reasoning of the advanced solution, as discussed below.
The academic reasoning depends on the basic rule of physics based on determinism, as shown in Figure 1(a); thus, most physical phenomena in nature are divided into two strands: determinism and indeterminism. Moreover, most physical phenomena must be certainly: 1) measurable property with quantitative and qualitative characteristics, 2) be reversible, and 3) be performable experiment (no sample-test) and it must always result the same results anytime and anywhere. It is a very important basis in Newtonian physics; as well as, an immutable physical principle.
Nevertheless, every complex system in nature does not conform to the rules of physics related to determinism, as shown in Figure 1(a). Therefore, the input and output of source in the natural complex system(s) is non-measurable and non-reversible, and unable to experiment in natural conditions. Thus, we define the scientific properties as “Performance Dilemma”, which represents the academic reasoning; which has originated from the times of Newton and Laplace. Nevertheless, most physicists and other scientists do not agree with this academic reasoning, what is the problem is there? This is because modern physics has not been exactly divided into determinism and indeterminism. Otherwise, we can verify the academic reasoning in the following contexts as premise.
2.2. Verifications of the Academic Reasoning
By the way, if any physicist, economist, or ecologist attempts to solve the com-
plexity with mathematics based on traditional physics, they certainly fail because a significant amount of money and time is needed to spend on this aspect. For example, for thermal systems, the stock market, or ecosystems, they would need to measure and gather a very large dataset, analyze it repeatedly at a high cost, and work on it for a long period. Therefore, they eventually failed to solve the algorithm in the complex systems; accordingly, nobody has successfully determined the solution to a complex system till now.
![]()
Figure 1. (a) Scope of physical science in nature; (b) Complex systems in nature & Basic model of complex system.
On the other hand, if it were possible to experiment on each complex system, the great Newton and other geniuses, as well as you, would have successfully performed these experiments under real circumstances. Newton could have found a perfect mathematical solution and decoded the algorithm and mechanisms of thermodynamic systems in nature, as well as addressed several other problems in physics. In the same way, Einstein could have easily completed the theory of quantum mechanics, and scientists would have already solved the three-body problem. It must be remembered it.
Similarly, Adam Smith, who conceived the “invisible hand,” along with the concepts of “supply and demand” and other economic theories, could have predicted stock market prices and become rich. In the same way, great Darwin could have extended this to ecosystems. Therefore, society would not require any physicists, economists, or ecologists; instead, would only need architects and accountants. In conclusion, we cannot exactly study on complexity under real circumstances; therefore, everybody ought to execute this using simulation under “virtual circumstances”. Despite this, if most scientists devoted to modern physics cannot confirm and acknowledge the academic reasoning as mentioned above in background, we cannot proceed to discuss any more.
2.3. Overview of the Advanced Solution
This section describes the main concept of the advanced solution. The experiments of the complex systems should be performed under ‘virtual circumstances’ by simulation, as and shown in Section 3. To realize this, we derive the proof in two ways, as shown in Figure 2(a) and Figure 2(b). The first one is through simulation by formal computer program MATLAB and the other is demonstrated with an analog-type simulator, which is operated by an electrotype [1] : Thus, the behavior of various types of complex systems can be studied in virtual circumstances. More details are given in Section 3.
2.4. Relationship to the Other Discipline in Science
We obtain very important information from the above description: the physical complex systems have no relationship with other fields of science, because these subjects in each system differ as shown in Table 1. For instance, it is different in terms of subjects such as various entropy, utility, or organic propagation; otherwise, the structure and algorithm are the same.
3. Experiment: Clarification of the Advanced Solution and its Validity
3.1. The Basic Concept in the Simulator
This section clarifies the validity and superiority of the advanced solution using the following sequence: [basic concept]?[experimentation]?[verification], because the new solution is too difficult to scientists, the principle of systems analysis method is unfamiliar with many physicists and the other scientists. Thus, the new solution is summarized in Figure 1(b).
(Basic concept in figure) For convenience, we consider an economic system in Figure 1(b), with a seller (G) and a buyer (H). G wishes to sell at a higher price, and H wishes to buy at a lower price, with time delay t between G and H. We can formulate the relationship between G and H as equivalent to a feedback system with a self-controlled property based on energy conservation. Thus, the associated equation is:
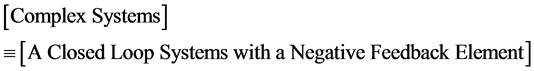
![]()
Table 1. Property of each complex system in sciences.
3.2. Process of Experimentation
The transfer function F(s) in Figure 1(b), given by 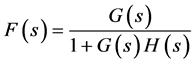 [4] ,
[4] ,
can be solved by mathematics in Appendix. Otherwise, we can be proved by simulation in two ways: by using the commercial program MATLAB Simulink, as shown in Figure 2(a). (Yellow line: input, blue line: output) or using an analog simulator with its results shown in Figure 2(b) (Blue line: input, yellow line: output). The electrotype simulator is accessible by anyone to perform these experiments. For this, we prepared a personal video clip on YouTube [5] for the readers.
3.3. Process of Verification
If the stock markets dealt with a feedback system, we can simulate easily using the formal analysis device MATLAB as shown Figure 2(a). If irregular stock information added into MATLAB or the analog simulator, the output would be realized display as shown in Figure 2(a); we obtain extremely irregular output, therefore, the daily stock price is endlessly irregular. Furthermore, As well as, if random function added into the simulator, the same output is obtained, as shown in Figure 2(b). Furthermore, the output is never a runaway, overflow, or an explosive. Hence, we can always realize the behavior of complexity as an irregularity similar to chaos, regularity similar to fractal behavior, self-conver- gence similar to self-organization, and initial phenomena similar to the butterfly effect [6]. More details can be found in [1] and [2] .
![]()
Figure 2. (a) Computer based on simulation program MATLAB Simulink and its response of a random function; (b) Response of a random function by analog simulator.
4. Result
This paper has successfully proved the mission of complexity by simulation as follows. 1) The complex systems could only be proven by simulation under “virtual circumstances”, because the complex systems are outside the scope of traditional physics based on determinism with reference to Figure 1(a). 2) The experiments on the complex systems were demonstrated with MATLAB and an analog simulator, as shown in Figure 2(a) and Figure 2(b). 3) The established older chaos theory was replaced with the new solution, as shown in Section 3.
However, it is never seen as a scientific result by scientists; the advanced solution proven by simulation is not normally used in modern physics, based on reductionism. It may lead to an incredible scientific result similar to the Copernican theory in science. Furthermore, it is superior to the established older chaos theory and it provides a complete and perfect solution for the mission of complexity.
5. Discussion
5.1. Consideration of the Paradoxical Problem in SFI
Despite this, many scientists do not welcome the advanced solution because it is beyond their belief, similar to the heliocentric theory by the great Galileo in the 15th century, and it has serious disadvantages for astrophysicists. For instance, it must withdraw the chaos theory as the established solution from now on, and, further research on this would not be necessary; the achievements of these scientists will be invalid in the future.
Nevertheless, many physicists require rigorous assessment of the solution by researchers, similar to Galileo. Therefore, many physicists avoid the new solution intentionally, stating that there is no merit in it and that they want to stick with the Ptolemaic theory. It appears to be a paradoxical problem. For instance, since 1984, the complex research organization Santa Fe Institute [3] established by Dr. Murray Gellman and other scientists have worked for complexity with older chaos theory. Nevertheless, we cannot receive their response from the SFI yet. Consequently, we feel that they should change their mission [3] and suspend their research work in future is inevitable. Thus, if the SFI has not known the new solution; they are goldfishes in fishbowl as mentioned by them.
5.2. Examples of Application
This section provides examples applicable to every science. In the case of real applications, such as in economics, the report in [7] describes how problems in economic systems can be solved, such as the prediction of stock price, the invisible hand, and the laws of supply and demand. Undoubtedly, this is a significant scientific achievement in economics. The other areas where this is applicable are nonlinear dynamics in modern science, such as quantum mechanics, climate change, and turbulence associated with indeterminism. It may be related to the uncertainty theory by the Heisenberg and Schrödinger equation. In the case of humanities, it can be applied to system science such as in system engineering and system dynamics; furthermore, it provides useful solutions for artificial intelligence research, the study of nuclear reactors in nonlinear dynamics, and other nonlinear applications in engineering science. The use of MATLAB (simulator) is highly recommended.
6. Conclusions
This paper has shown the advanced solution for the mission of complexity by the following steps: hypothesis, experiment and verifications; it has been proven sufficiently by simulation under virtual circumstances based on indeterminism; it had not ever seen achievements in modern sciences. However, the advanced solution has solved by the other discipline of science, which is very difficult to the whole scientists around the world. Moreover, it is entirely different from the older chaos theory, as if the Copernican theory and its validity cannot be questioned. Therefore, we need not the established solution as the older chaos theory any more in future; it is not perfect and unavailable for the new solution.
Nevertheless, it has no advantage to many physicists, specializing in chaos, and they would not welcome the new solution. Nevertheless, we expect that physicist Dr. Murray Gell-Mann and his cooperator in SFI consider the solution deeply and respond their opinion to us. Thus, we are not “goldfish in bowl” as they mentioned it before. However, we can conclude that the complexity is a solvable problem. In addition, all scientists ought to begin to study the MATLAB in formal science and we must exclude the mysticism in sciences.
Appendix: Mathematical Solution for Feedback-Systems [4]
The transfer function F(s) in Figure 1(b), given by 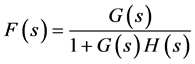 [4] .
[4] .
We can be solved by mathematics as below. If the input source is U(s) is
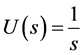 , and the system equation is
, and the system equation is
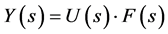 (1)
(1)
where,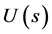 : input source,
: input source,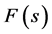 : transfer function,
: transfer function,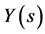 : the output source.
: the output source.
Therefore, we substitute the equation as below [4] .
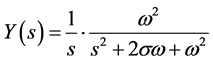 (2)
(2)
where, : Laplace operator,
: Laplace operator, : damping factor,
: damping factor, : constant. We can obtain the original output function y(t) from the Y(s) as below
: constant. We can obtain the original output function y(t) from the Y(s) as below
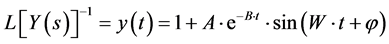 (3)
(3)
where, 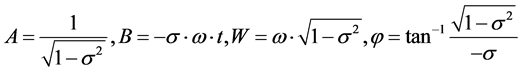
Please watch the Figure 2(b) in right side upper graph, which is equivalent with Equation (3).

Submit or recommend next manuscript to SCIRP and we will provide best service for you:
Accepting pre-submission inquiries through Email, Facebook, LinkedIn, Twitter, etc.
A wide selection of journals (inclusive of 9 subjects, more than 200 journals)
Providing 24-hour high-quality service
User-friendly online submission system
Fair and swift peer-review system
Efficient typesetting and proofreading procedure
Display of the result of downloads and visits, as well as the number of cited articles
Maximum dissemination of your research work
Submit your manuscript at: http://papersubmission.scirp.org/
Or contact jmp@scirp.org