1. Introduction
The motion of single electrons in atomic matter is basically well understood. However, our knowledge of the dynamics of few-electron complexes in external fields is still incomplete. We mention here two typical examples.
For the ionization of a neutral atom by slow electron impact, a simple phase space consideration suggests a threshold cross-section being linear in the excess energy, i.e.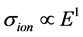 . This is, however, in conflict with many experimental data. Actually, Wannier [1] has treated the ionization of a hydrogen-like target by electrons within the frame of classical Lagrange equations, and arrived instead of the linear law at a power law with fractional exponent
. This is, however, in conflict with many experimental data. Actually, Wannier [1] has treated the ionization of a hydrogen-like target by electrons within the frame of classical Lagrange equations, and arrived instead of the linear law at a power law with fractional exponent
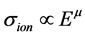 (1)
(1)
the exponent given by
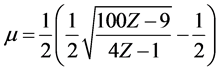 (2)
(2)
Z being the nuclear charge. For hydrogen (2) predicts the numerical value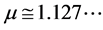 . Surprisingly, that value is in favourable agreement also for other neutral atoms [2] . Obviously, Wannier has successfully described the motion of an electron pair in an external Coulomb field. It is far from trivial how (2) derives from quantum mechanics see e.g. [3] [4] .
. Surprisingly, that value is in favourable agreement also for other neutral atoms [2] . Obviously, Wannier has successfully described the motion of an electron pair in an external Coulomb field. It is far from trivial how (2) derives from quantum mechanics see e.g. [3] [4] .
The phenomenon of superconductivity is well described by a theory developed by Bardeen, Cooper and Schriefer (hereafter shortly BCS) [5] . The BCS theory rests on the assumption that electric current is transported by electron pairs, so-called Cooper-pairs, rather than by single electrons. According to BCS the attraction between the electrons emerges from an exchange of virtual phonons. Therefore the existence of Cooper-pairs seems to be a many-body effect where “many” refers to the number of nuclei.
The present paper investigates three-body Coulomb systems (nucleus + 2 electrons) within the frame of quantum mechanics. We re-derive (2) for ionization and present an alternative electron-electron attraction mechanism for electron pairs in an external Coulomb field.
The paper is organized as follows. Section 2 introduces a suitable set of coordinates to treat the electron pair as a whole. Section 3 derives a fictitious force which deforms the electrostatic potentials and presents dominantly correlated wave functions for electron pairs. Section 4 presents a discussion of the quantum version of the classical Wannier ionization theory. In particular we investigate intrinsic vibrations of moving electron pairs. Finally, we describe a possible travel of an electron pair through a linear chain of Rydberg atoms. Concluding remarks are presented in Section 5.
2. Geometrical Aspects
The treatment of three bodies (two electrons + nucleus) in the centre-of-mass system needs in general six space coordinates. Single electron coordinates are certainly not suitable for correlation studies. In this paper we restrict ourselves to pure S-states. Body-fixed coordinates coincide then with lab-fixed coordinates. We fall then down to three space coordinates only. This was already remarked long ago by Sommerfeld [6] . We use here collective coordinates closely related to the tensor of inertia of the 3-body complex. Since the nucleus of any two-electron atom is much heavier than an electron we put the centre-of-mass into the nucleus. One principal axes (here z-axis) of inertia is orthogonal to the particle plane. Its moment of inertia reads in atomic units
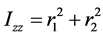 . (3)
. (3)
Without loss of generality we put the principal x-axis into the direction of the smallest moment. A right-handed coordinate system we obtain provided we use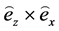 as y-axis.
as y-axis.
In the above basis of principal axes the electron positions are given by, see [7]
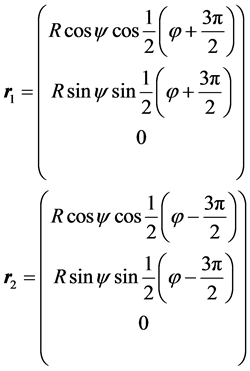 (4)
(4)
It is easily verified that the inertia tensor is diagonal, i.e.
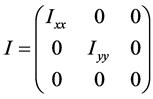 (5)
(5)
Our coordinates R and ψ are given by its components
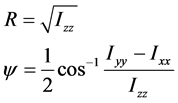 (6)
(6)
Note that the moments 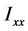 and
and 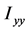 cannot be used as independent coordinates because of the Pythagoras relation
cannot be used as independent coordinates because of the Pythagoras relation 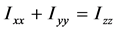 for a plane body.
for a plane body.
The angles ψ and φ may be expressed in terms of the electron position vectors. To do that we first calculate the squared interparticle distances. From (4) we get for the squared interparticle separations
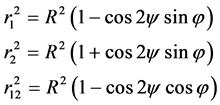 (7)
(7)
with the e-e-separation 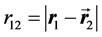 and extract from (7) easily
and extract from (7) easily
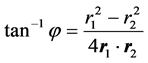 (8)
(8)
 (9)
(9)
Note, however, that (9) holds only on the ridge (see Section 3), i.e.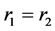 .
.
Our coordinates may be regarded as standard spherical coordinates in a three- dimensional half-space. That space is spanned by 3-body configurations rather of single electron positions. The kinetic energy of the electron pair as one was already calculated in [7] . We obtained [7]
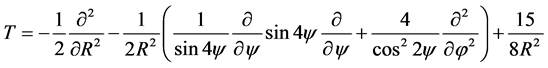 (10)
(10)
and observe that the angular part coincides with the squared orbital angular momentum provided we introduce the latitude angle ![]() instead of ψ. The range of ψ is here
instead of ψ. The range of ψ is here![]() .
.
The three-dimensional halfspace is spanned by the Cartesian coordinates
![]() (11)
(11)
and consists of the elements![]() . Keeping in mind that we treat here electron pairs as one rather than single electrons it is not too surprising that inertia components are useful coordinates.
. Keeping in mind that we treat here electron pairs as one rather than single electrons it is not too surprising that inertia components are useful coordinates.
From the definition it is obvious that ![]() corresponds to collinear electron-nucleus-electron configurations because the moment
corresponds to collinear electron-nucleus-electron configurations because the moment![]() . It makes no sense to extend ψ to negative values since negative ψ-values generate the same moments of inertia which would lead to a double-counting of configurations. We remark that the angular motion occurs on a hemisphere, below the northern hemisphere for convenience. This is in contrast to all other treatments which operate in a 6-dimensional 2-electron space. The next section uses this advantage to study directly the propagation of electron pairs rather than of single electrons.
. It makes no sense to extend ψ to negative values since negative ψ-values generate the same moments of inertia which would lead to a double-counting of configurations. We remark that the angular motion occurs on a hemisphere, below the northern hemisphere for convenience. This is in contrast to all other treatments which operate in a 6-dimensional 2-electron space. The next section uses this advantage to study directly the propagation of electron pairs rather than of single electrons.
3. Propagation of Electron-Pair Waves
Classical zero-energy trajectories have been calculated by Wannier [1] . According to his analysis only a cone with a small angular aperture contributes at zero energy, in our coordinates![]() . This region is the environment of an unstable equilibrium configuration. That configuration may be easily represented with our coordinates. To this end we write the potential energy of the atom, see [7] , in our coordinates. We get with help of (7)
. This region is the environment of an unstable equilibrium configuration. That configuration may be easily represented with our coordinates. To this end we write the potential energy of the atom, see [7] , in our coordinates. We get with help of (7)
![]() (12)
(12)
with the charge function ![]() given by,
given by,
![]() (13)
(13)
The equilibrium point is located at![]() ,
,![]() . This corresponds to a collinear configuration with equal electron nucleus distances
. This corresponds to a collinear configuration with equal electron nucleus distances![]() . This point is actually a saddle point with the Taylor expansion
. This point is actually a saddle point with the Taylor expansion
![]() , (14)
, (14)
the coefficients given by
![]() (15)
(15)
We simplify now the kinetic energy to its value on the equator (ψ = 0) of the hemisphere and use the potential expansion (14). We arrive thus at the wave equation to be solved
![]() (16)
(16)
Previous calculations using hyperspherical coordinates have shown that correlation is most important at radii ![]() where the Wannier radius is given by
where the Wannier radius is given by
![]() . (17)
. (17)
The Wannier radius diverges at threshold (E = 0). We need therefore an asymptotic solution of the wave equation. Below we take into account the terms in the wave equation which scale like ![]() and
and![]() . Powers like
. Powers like![]() ,
, ![]() will be neglected. The angular cone we limited to quadratic powers, higher order terms will be neglected.
will be neglected. The angular cone we limited to quadratic powers, higher order terms will be neglected.
In order to get an overview on solutions we consider for the moment an adiabatic approximation, i.e. we put R = constant, see Macek [8] . Actually in the following we go beyond ref [8] . In the adiabatic approximation we are left with an harmonic oscillator plus one antioscillator. The eigenfunction of the oscillator is
![]() with
with ![]() and with the eigenvalue
and with the eigenvalue![]() .
.
Analogous to the oscillator we get for the antioscillator the eigenfunction
![]() with
with ![]() and the eigenvalue
and the eigenvalue ![]() .
.
This adiabatic approach is far from being exact, but gives us hints how to proceed. We go now beyond the adiabatic approximation, and expect an angular part of the wavefunction which constitutes travelling waves along the angular directions. A suitable ansatz is
![]() . (18)
. (18)
With an additional amplitude A we construct the complete wavefunction in the form,
![]() (19)
(19)
In order to retain flexibility for the angular function we have allowed for slowly varying amplitudes p(ψ) and q(φ) in equation (18); we require for (15) the following boundary conditions
![]() ; (20)
; (20)
and for outgoing flux along φ
![]() (21)
(21)
whereas for incoming flux we need
![]() (22)
(22)
Dominant correlation effects at zero total energy emerge from a deformation of the 3-body Coulomb potential surface. A pilot study for the two-electron atom based on a liquid drop model has shown that a fictitious force emerges from surface tension [9] . The present treatment goes beyond any model but solves the wave equation exactly.
The fictitious force is here hidden in the cross-term of the second derivative with respect to R, i.e.
![]() (23)
(23)
We show below that both driving terms of ![]() and
and ![]() are
are![]() .
.
These terms modify the curvature of the potential surface; i.e. they modify the coefficients ![]() and
and ![]() in (14).
in (14).
To this end we substitute now (18, 19) into the wave equation, use for the amplitude the ansatz
![]() (24)
(24)
and solve the wave equation in the Coulomb zone for large values of R. I.e. we neglect terms of the order![]() ,
,![]() . Thus we find
. Thus we find
![]() (25)
(25)
We now determine the non-adiabatic width γ in (18) and the front function![]() . To this end we treat the ψ-dependent part of the wave equation as eigenvalue problem, i.e.
. To this end we treat the ψ-dependent part of the wave equation as eigenvalue problem, i.e.
![]() (26)
(26)
(26) may be regarded as wave equation for an harmonic oscillator located in a moving frame caused by the evolution along R. This causes a fictitious force which manifests itself here as a modification of the potential surface curvature.
Equation (26), finally, becomes an equation for ![]() alone
alone
![]() (27)
(27)
Inspection of (27) shows that the fictitious force mentioned above has changed the potential curvature ![]() by the amount
by the amount
![]() (28)
(28)
the shift being independent of R, see below. We eliminate all terms ![]() by asking to vanish the second bracket term in (27)
by asking to vanish the second bracket term in (27)
![]() . (29)
. (29)
This is a Riccati equation which can be solved exactly. We put ![]() and find for the constant
and find for the constant ![]()
![]() (30)
(30)
Because of the boundary condition (20) we have rejected the solution ![]()
The appendix shows that the function ![]() is a finite polynomial in the variable
is a finite polynomial in the variable ![]() with eigenvalue given by
with eigenvalue given by
![]() (31)
(31)
This is a typical oscillator spectrum except that only even values of M occur, and the zero-point energy is one unit instead of 1/2. The first three polynomials standardized to ![]() read explicitly
read explicitly
![]() (32)
(32)
We come now to the function ![]() which treats the antioscillator
which treats the antioscillator
![]() . The equation for
. The equation for ![]() analogous to that for
analogous to that for ![]() (26) is
(26) is
![]() (33)
(33)
The corresponding equation for ![]() reads
reads
![]() (34)
(34)
We eliminate all terms ![]() which determines the λ. Thus we have to solve the Riccati equation
which determines the λ. Thus we have to solve the Riccati equation
![]() . (35)
. (35)
Here we observe that the curvature of the potential has been changed to
![]() (36)
(36)
with![]() . Remarkably we shift in (36) depends on the parameter σ, the shift is therefore dependent on the direction of radial wave propagation. For an incident wave (σ < 0) the curvature
. Remarkably we shift in (36) depends on the parameter σ, the shift is therefore dependent on the direction of radial wave propagation. For an incident wave (σ < 0) the curvature ![]() is reduced whereas an outgoing wave observes a larger curvature. In terms of
is reduced whereas an outgoing wave observes a larger curvature. In terms of ![]() Equation (35) is a quadratic equation whose solutions may be cast into the form of parameters for outgoing and incoming waves along the angle φ. With help
Equation (35) is a quadratic equation whose solutions may be cast into the form of parameters for outgoing and incoming waves along the angle φ. With help ![]() we identify the parameters
we identify the parameters
![]() (37)
(37)
The function![]() , finally, is determined by
, finally, is determined by
![]() (38)
(38)
The Appendix shows that due to the travelling wave boundary condition ![]() is a finite polynomial with imaginary eigenvalues given by
is a finite polynomial with imaginary eigenvalues given by
![]() (39)
(39)
Electron exchange is described in our coordinates by the replacement![]() , the other coordinates remain unchanged [7] . The Appendix shows the symmetry property
, the other coordinates remain unchanged [7] . The Appendix shows the symmetry property
![]() (40)
(40)
We conclude, therefore, that even quantum numbers ![]() describe singlet states whereas odd numbers
describe singlet states whereas odd numbers ![]() belong to triplets.
belong to triplets.
We come, finally, to the radial function A(R), see (24). That function satisfies the equation
![]() (41)
(41)
With the ansatz (24) we derive relations for the parameters σ, and τ,
![]() (42)
(42)
4. Results and Discussion
So far we have solved the stationary wave equation at zero energy![]() . Wannier has pointed out that classical trajectories remain at small but finite energy |E| unchanged [1] . We observe here a quantum situation analogous to Wanniers observation. From the stationary wave equation for
. Wannier has pointed out that classical trajectories remain at small but finite energy |E| unchanged [1] . We observe here a quantum situation analogous to Wanniers observation. From the stationary wave equation for ![]() we see immediately that the energy parameter E enters any wavefunction only in the combinations
we see immediately that the energy parameter E enters any wavefunction only in the combinations ![]() and
and![]() , i = 0, 1, 2 with
, i = 0, 1, 2 with![]() . Therefore the zero-energy angular function (18) remains unchanged for small but finite energy. Only the radial wavefunction carries an energy dependence on the form
. Therefore the zero-energy angular function (18) remains unchanged for small but finite energy. Only the radial wavefunction carries an energy dependence on the form![]() .
.
Our analysis gives insight into the process of electronic excitation. Let us consider a hydrogen-like target bombarded by a slow electron. Due to the attractive
interaction ![]() the three bodies (nucleus + 2 electrons) are forced into a
the three bodies (nucleus + 2 electrons) are forced into a
collinear configuration (electron-nucleus-electron). In this configuration the
unstable repulsive interaction ![]() becomes active. The radial wave
becomes active. The radial wave
function carries in the incoming wave mode a factor ![]() which increases for decreasing values of R because
which increases for decreasing values of R because![]() , see (37). This is accompanied by a turn of the wavefront towards the potential ridge located at
, see (37). This is accompanied by a turn of the wavefront towards the potential ridge located at![]() . This is because the incoming wave component along φ is controlled by the same parameter
. This is because the incoming wave component along φ is controlled by the same parameter![]() . The electrons move now along R on the top of the antioscillator. A dominantly correlated electron pair has been born. That pair however, does not fall into the nucleus because of a centrifugal barrier given by
. The electrons move now along R on the top of the antioscillator. A dominantly correlated electron pair has been born. That pair however, does not fall into the nucleus because of a centrifugal barrier given by
![]() , see (10). This barrier constitutes a turning surface for the pair, and the
, see (10). This barrier constitutes a turning surface for the pair, and the
pair switches after reflexion into the outgoing wave mode. The outgoing radial wavefunction carries now an amplification factor ![]() which increases for increasing values of R. The same parameter
which increases for increasing values of R. The same parameter![]() , see again (37), turns the pair wavefront away from the ridge. i.e. slightly below threshold one electron escapes and the other is trapped into a Rydberg state. Slightly above threshold both electrons escape. As a result in both cases the pair decays except the long range tail of the Coulomb potential
, see again (37), turns the pair wavefront away from the ridge. i.e. slightly below threshold one electron escapes and the other is trapped into a Rydberg state. Slightly above threshold both electrons escape. As a result in both cases the pair decays except the long range tail of the Coulomb potential ![]() leads to an outer turning below threshold. Then we obtain a novel kind of resonance. The electrons, hoever, do not perform circular orbits as one might expect. They do a stretch motion within a high Coulomb level whose degeneracy is removed by the bending mode oscillator. The imaginary stretch mode oscillator determines the width of the levels. That entirely different spectrum structure replaces standard double Rydberg states of the form
leads to an outer turning below threshold. Then we obtain a novel kind of resonance. The electrons, hoever, do not perform circular orbits as one might expect. They do a stretch motion within a high Coulomb level whose degeneracy is removed by the bending mode oscillator. The imaginary stretch mode oscillator determines the width of the levels. That entirely different spectrum structure replaces standard double Rydberg states of the form![]() . Above threshold the wavefront falls down from the ridge. We arrive then at single escape, one electron captured in a Rydberg orbital. Under that viewpoint the final state of ionization near threshold may be regarded as decay of an electron pair. The key point of this mechanism is that the fictitious force, see (34), has opposite signs in the incoming and outgoing channel. This effect is entirely foreign to standard scattering theory.
. Above threshold the wavefront falls down from the ridge. We arrive then at single escape, one electron captured in a Rydberg orbital. Under that viewpoint the final state of ionization near threshold may be regarded as decay of an electron pair. The key point of this mechanism is that the fictitious force, see (34), has opposite signs in the incoming and outgoing channel. This effect is entirely foreign to standard scattering theory.
We investigate now the ionization cross section of an hydrogen-like atom by electron impact near threshold. The total cross-section is then given by the ratio of outgoing flux divided by incoming flux, i.e.
![]() (43)
(43)
with
![]() (44)
(44)
We rewrite the second equation of (42) as pair of aggregates for outgoing and incoming flux, and subtract the incoming component from the outgoing one. We find
![]() (45)
(45)
which yields after trivial rearrangements
![]() (46)
(46)
(46) coincides in the vibrational ground state (N = 0) with Wannier’s formula (2). In agreement with Wannier we also confirm that the total threshold ionization cross-section is independent of the parameter![]() . There is, however, one difference with respect to Wannier’s classical analysis. Wannier had to assume that this cross section is independent of the energy sharing between the electrons; i.e. the singly differential cross-section is flat. Any energy sharing is equally likely. The energy sharing is in our framework hidden in the coordinate φ. Our singly differential cross-section is proportional to
. There is, however, one difference with respect to Wannier’s classical analysis. Wannier had to assume that this cross section is independent of the energy sharing between the electrons; i.e. the singly differential cross-section is flat. Any energy sharing is equally likely. The energy sharing is in our framework hidden in the coordinate φ. Our singly differential cross-section is proportional to
![]() (47)
(47)
Only the groundstate N = 0 is independent of φ. We conclude that only the groundstate shows a uniform energy sharing; all triplet events and excited singlets do not.
According to Wannier the electrons escape sharply into opposite directions corresponding to an angular distribution![]() . Experimental data of the ionization of H(1s) by electrons do not show a clear peak in that direction corresponding to the Gaussian
. Experimental data of the ionization of H(1s) by electrons do not show a clear peak in that direction corresponding to the Gaussian![]() . The observed angular distribution seems to be broader than the Gaussian. Actually, our angular distribution is proportional to
. The observed angular distribution seems to be broader than the Gaussian. Actually, our angular distribution is proportional to
![]() (48)
(48)
We conclude that excitation of a bending mode corresponding to ![]() may have modified the distribution. The experiments, however, are not good enough to extract the quantum number M [10] .
may have modified the distribution. The experiments, however, are not good enough to extract the quantum number M [10] .
The observation of stretch vibrations is difficult because the cross-sections become rather small for increasing excitation![]() . Table 1 shows how the exponent μ increases with increasing N.
. Table 1 shows how the exponent μ increases with increasing N.
From Table 1 it is evident that near threshold the mode ![]() controls the slope of the threshold cross-section because the cross-sections are strongly depressed for increasing values of N. According to our analysis the final state after ionization near threshold may be regarded as decay of an electron pair.
controls the slope of the threshold cross-section because the cross-sections are strongly depressed for increasing values of N. According to our analysis the final state after ionization near threshold may be regarded as decay of an electron pair.
The immediate decay of a pair after its creation may be employed to transport an electron through a solid. We consider for simplicity a linear chain of one- electron atoms, and hit an atom at one chain end by a slow electron. According to our analysis the two electrons enter into a collinear configuration. During the further penetration of the impact electron a pair will be created. After the pair
![]()
Table 1. Cross-section exponents for various stretch vibrations.
reflection from the turning surface the pair decays under the influence of the repulsive fictitious force between the electrons. One electron will be trapped into a Rydberg orbital whereas the other one escapes. The next neighbour atom experiences the escaping electron as an incoming one in its own frame. It will be attracted by that atom to form a new pair which creates after its decay another pair in the atom #3. At the end of the chain we obtain again one free electron. Concluding, an observer from outside may say that one electron has travelled through the chain. Actually, a macroscopic transport of electric charge has not taken place, but a wave of electron pairs has propagated.
5. Conclusions
The reader of this article might claim that the fictitious force derived here and its unusual consequences have emerged due to artefacts from the use of rather unusual coordinates. We stress, however, that this criticism is not justified. We believe that the three-body Coulomb problem is not separable in any coordinate system. The deformation of the potential surface as described above must always happen due to the non-separability of the system. Our coordinates have the great advantage that we are able to treat exactly, and surprisingly simply, the non- separability between radial and angular motion.
We remark that except for atomic hydrogen all atomic and molecular systems are non-separable. Our above treatment may therefore be regarded as roadmap to treat non-separable systems. In the present case of two electrons a NAIV consideration would have expected highly excited double Rydberg states of the form ![]() with
with![]() . We have, however, seen that they are suppressed close to threshold and replaced by a pair formation where the electrons are not on Bohr- like orbits. Essential has here been that the electrons charge centre is in an unstable equilibrium configuration.
. We have, however, seen that they are suppressed close to threshold and replaced by a pair formation where the electrons are not on Bohr- like orbits. Essential has here been that the electrons charge centre is in an unstable equilibrium configuration.
Such unstable equilibrium configurations, however, seem always exist. We have shown that the three-electron equilibrium is an equilateral triangle, one electron in each corner and the nucleus in the center [11] . Instead of electron pairs we expect then electron trios. Four electrons in the unstable equilibrium are located in the corners of a tetraeder which is expected to allow for electron quadruples, and so on.
The prototype of a non-separable system is the simplest molecule![]() . It is well-known that the Born-Oppenheimer approximation becomes shaky for vibrational states in a high electronic excitation. Our treatment is well suited to treat that situation where non-adiabatic coupling becomes strongest.
. It is well-known that the Born-Oppenheimer approximation becomes shaky for vibrational states in a high electronic excitation. Our treatment is well suited to treat that situation where non-adiabatic coupling becomes strongest.
Acknowledgements
This worked was started long ago under the support by DFG contract SFB 276. The author acknowledges gratefully that support during 1970-80.
Appendix
We investigate here the functions ![]() and
and![]() , see (16, 26, 34). Equation (16) is a solution of the wave equation if and only if p and q satisfy eigenvalue equations.
, see (16, 26, 34). Equation (16) is a solution of the wave equation if and only if p and q satisfy eigenvalue equations.
We start with p. Its eigenvalue equation reads after multiplication with ![]()
![]() (A1)
(A1)
where ![]() is the eigenvalue.
is the eigenvalue.
For the moment it is convenient to put![]() . (A1) becomes then
. (A1) becomes then
![]() (A2)
(A2)
We try to solve with a power series expansion, i.e.
![]() (A3)
(A3)
The recurrence relation for the coefficients ![]() leads to its asymptotic form (
leads to its asymptotic form (![]() )
)
![]() (A4)
(A4)
The asymptotic form of ![]() is therefore
is therefore
![]() . (A5)
. (A5)
That destroys however the incoming wave in a classically forbidden region
![]() .
.
As in the bound state situation we overcome this difficulty by a truncation of the power series. We stress, however, that a travelling wave boundary condition forces us to that step. This has nothing to do with normalization.
To this end we return to (A1) and solve it with the expansion
![]() (A6)
(A6)
After trivial rearrangements this leads to the recurrence relation
![]() (A7)
(A7)
The condition for truncation is ![]() from which the real
from which the real
eigenvalue ![]() or
or
![]() (A8)
(A8)
follows. It is evident from (A1) that only functions even in ![]() solve the differential equation. For an odd function we would have
solve the differential equation. For an odd function we would have ![]() and
and ![]() =
=
finite. The term ![]() would then diverge.
would then diverge.
The first three polynomials standardized to ![]() read
read
![]() (A9)
(A9)
The function ![]() we treat along the same lines above. We try to solve (38) with a power series expansion,
we treat along the same lines above. We try to solve (38) with a power series expansion,
![]() , (A10)
, (A10)
and show its asymptotic behaviour![]() . Again this contradicts to our boundary condition (20) and we conclude that the series must be a finite polynomial. We omit here the details of a straightforward investigation and come immediately to the result. The expansion (A9) leads to the recurrence relation
. Again this contradicts to our boundary condition (20) and we conclude that the series must be a finite polynomial. We omit here the details of a straightforward investigation and come immediately to the result. The expansion (A9) leads to the recurrence relation
![]() (A11)
(A11)
At a finite polynomial of degree ![]() we arrive with the imaginary eigenvalue
we arrive with the imaginary eigenvalue
![]() (A12)
(A12)
The first three polynomials standardized to ![]() (N even) and
(N even) and ![]() (N odd) read
(N odd) read
![]() (A13)
(A13)
![]()
Submit or recommend next manuscript to SCIRP and we will provide best service for you:
Accepting pre-submission inquiries through Email, Facebook, LinkedIn, Twitter, etc.
A wide selection of journals (inclusive of 9 subjects, more than 200 journals)
Providing 24-hour high-quality service
User-friendly online submission system
Fair and swift peer-review system
Efficient typesetting and proofreading procedure
Display of the result of downloads and visits, as well as the number of cited articles
Maximum dissemination of your research work
Submit your manuscript at: http://papersubmission.scirp.org/
Or contact jmp@scirp.org