Spatial Correlation Characteristics Analysis of Multi-Beam Channels of Mobile Satellite System ()
1. Introduction
The development of wideband multimedia service has raised demand of speed and spectrum efficiency of a new generation mobile-satellite communication system. In the condition of limitation of power, it is significant to make use of space resource to increase system performance. Under the influence of the distribution of scatterer near the receiver antenna, channel fading has spatial correlation in mobile-satellite communication system.
Compatible with LTE standard will be a trend for the new generation of mobile-satellite communication system. Because multiple-input multiple-output (MIMO) is an important part of LTE standard, the research of channel spatial correlation has certain reference value.
Currently, the commonly used classical satellite channel models are Loo model, Lutz model, Fontan model etc.
In terms of research regarding channel spatial correlation characteristics, a spatial Rayleigh-fading correlation model for MIMO has been proposed in [1]. This model assumes uniform distribution of the scatterers with respect to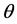 , the angle-of-arrival (AOA) at the subscriber unit. The model also assumes that all received rays are equal in power, which is not a realistic assumption for multipath environments. An extension of this model for Rician-fading channels appeared in [2], which assumes von Mises angular distribution for scatterers.
, the angle-of-arrival (AOA) at the subscriber unit. The model also assumes that all received rays are equal in power, which is not a realistic assumption for multipath environments. An extension of this model for Rician-fading channels appeared in [2], which assumes von Mises angular distribution for scatterers.
Moreover, Mahmoud developed a geometrical based hyperbolic channel (GBHC) model for macrocells in [3]. A combination of the model in [3] and scalar stochastic fading model for local scatterers was presented in [4]. The GBHC model is a two-dimension model, which assumed that the scatterers are arranged circularly around the mobile station (MS), and the distances between the MS and scatterers are subject statistically to a hyperbolic distribution.
This paper mainly researches spatial correlation of multi-beam channels of mobile satellite system. Different from current spatial correlation research, we create a three-dimension channel model based on stochastic geometric model, which considers the height of scatterers, and deducts spatial correlation coefficient among channels with numeric calculation and analysis.
2. Satellite Channel Model
2.1. Multi-Beam Model
Satellite multiple beam antenna (MBA) began to develop in the 1970s to 1980s. Single Feed per Beam (SFB) technology was adopted in the early stage. Later, multiple feeds per beam (MFB) technology was employed. Compared with phased-array antenna, feed beam of MBA is more narrow, and stronger. So the MBA has been widely used in satellite mobile communication systems in 1990s.
According to the structure, MBA can be divided to three categories: phased array antenna, reflector antenna and lens antenna. In this paper, we use reflector antenna to create multi-beam model.
As is shown in Figure 1, the distance of ground receiver to center of component beam is different, which makes the signal strength varies.
Figure 2 shows the space relationship among satellite, user u and component beam center n. h is the height of satellite orbit. R is radius of the earth.
According to Figure 2, suppose that 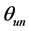 is the angle of ground receiver u to satellite and component beam center n to satellite,
is the angle of ground receiver u to satellite and component beam center n to satellite,  can be given by
can be given by
 (1)
(1)
where dSn and dSu are the distance between satellite and component beam center n and user u respectively. 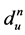 is the distance between sub-satellite point and user u.
is the distance between sub-satellite point and user u.
![]()
Figure 1. Component beam schematic diagram.
Suppose that 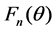 is the normalized far-field radiation pattern of component beam, the adoption of different radiation pattern results different antenna gain, when the direction angle is the same.
is the normalized far-field radiation pattern of component beam, the adoption of different radiation pattern results different antenna gain, when the direction angle is the same. 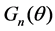 represents the antenna gain of the nth component beam. The
represents the antenna gain of the nth component beam. The 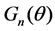 can be written as
can be written as
 (2)
(2)
where  can be calculated by (1), Gmax,n is the maximum gain of the nth component beam.
can be calculated by (1), Gmax,n is the maximum gain of the nth component beam.
2.2. Mobile Satellite Channel Model
In satellite communication, a signal is fading during propagation. Those fading may cause by environment and various attenuation facts, for instance cloud attenuation, rain attenuation and ionospheric scintillation. Taking into account this paper research mainly discusses spatial correlation, since attenuation facts like cloud attenuation and ionospheric scintillation are stay the same for a long time, we focus on the influence of ground environment near receiver, namely the multipath which arise from scattering, reflection, refraction or diffraction of the radiated energy off scatterers that lie in the environment.
For satellite communication, typically the height of the ground receiver is lower than nearby scatterers. The received signals in the both horizontal and
![]()
Figure 2. Three-dimension component beam model.
vertical plane are distributed. While establishing the channel model, we need to consider the height of scatterers, so the traditional two-dimensional geometric channel model no longer applies. Assuming that scatterers are distributed in a right cylinder which has ground receiver as it bottom center, a three-dimension geometry channel model is shown in Figure 3. A large picture of ground receiver in the model is shown in Figure 4.
For a downlink of satellite communication system, we assume that p and q are the number of satellite antennas, l and m are the number of ground antennas,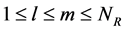
 . Nr and Nr are the maximum number of transmitting antenna and receiving antenna. The received signal is given by
. Nr and Nr are the maximum number of transmitting antenna and receiving antenna. The received signal is given by
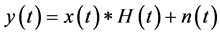 (3)
(3)
where, H(t) is channel impulse response, n(t) is noise. 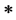 represents convolution.
represents convolution.
The received signal includes direct-path and multipath component in satellite communication system. So the channel impulse response is given by
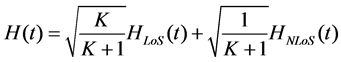 (4)
(4)
where HloS(t) is impulse response of direct-path, HNLoS(t) is impulse response of multipath. HloS(t) and HNLoS(t) are both NT × NR matrix. K is Rician Index, which describes ratio of direct-path power and multipath power (unit is dB). The value of K depends on angel of elevation from ground receiver to satellite, carrier frequency and environment around receiver. In this paper, since the interval between ground antennas is much small than shadow fading in different states, we
![]()
Figure 3. 3-Dimension geometry channel model.
![]()
Figure 4. Large picture of ground receiver.
can approximate that received signal shallow fading of two antennas are the same.
In the model shown in Figure 3 and Figure 4, Rm and Rl are the mth and the lth antenna in ground receiver respectively, Tp and Tq are the pth antenna and the qth antenna in satellite respectively. x − y plane is parallel to horizontal surface, and is perpendicular to OOR. OR is the midpoint of two antennas Rm and Rl ground projection line. OS is the point of intersection of x axis and y axis and also the midpoint of x − y plane projection line of two antennas Tp and Tq. OT is the center of transmitting antenna array. HS,max is the maximum height of scatterers distribution. RS,max is the maximum range of scatterer distribution (the maximum radius). ![]() and
and ![]() represent projection of Tp and Tq in x − y plane respectively.
represent projection of Tp and Tq in x − y plane respectively. ![]() is the angle between projection of transmitting antennas array
is the angle between projection of transmitting antennas array ![]()
![]() and x axis.
and x axis. ![]() is the angle of receiving antennas array Rm Rl and x axis.
is the angle of receiving antennas array Rm Rl and x axis. ![]() is the angle of Rm Rl and x − y plane.
is the angle of Rm Rl and x − y plane. ![]() is the angle between segment of receiving antenna arrays and satellite and x-y plane, namely the elevation. dT and dR is the distance of adjacent antenna on satellite and ground respectively.
is the angle between segment of receiving antenna arrays and satellite and x-y plane, namely the elevation. dT and dR is the distance of adjacent antenna on satellite and ground respectively. ![]() is the central angle between sub-satellite point and receiver antenna. To facilitate the analysis, da→b represent distance of a and b. the distance of
is the central angle between sub-satellite point and receiver antenna. To facilitate the analysis, da→b represent distance of a and b. the distance of ![]() and OR is
and OR is![]() . And the distance of
. And the distance of ![]() and OT is
and OT is ![]() .
.
According to the model, the impulse responses of sub channel from Tp to Rl can be written as
![]() (5)
(5)
Since the large number of hypothetical scatterers in the model, let Sn be the nth scatterer. Let RS,max and HS,max represent the radius and height of cylinder in the model, namely, the maximum distance and height of scatterers distribution. RS(n) is the distance between OR and Sn projection in x-y plane,![]() . HS(n) is the height of Sn,
. HS(n) is the height of Sn,![]() . Without considering the height of ground antennas, the nth scatterer elevation in scattering path can be approximately shown as
. Without considering the height of ground antennas, the nth scatterer elevation in scattering path can be approximately shown as![]() .
. ![]() and
and ![]() respectively describe the leaving angle and arriving angle of the nth path, which is influenced by Sn. In the model,
respectively describe the leaving angle and arriving angle of the nth path, which is influenced by Sn. In the model, ![]() ,
, ![]() , RS(n), HS(n) and
, RS(n), HS(n) and ![]() are all random variables.
are all random variables.
In multi-beam channels of mobile satellite system, the impulse responses of sub channel from Tp to Rl can be written in terms of (5). Considering the influence from component beam on to received signal, the direct-path component of the channel response can be written as
![]() (6)
(6)
And multipath component of the channel response can be written as
![]() (7)
(7)
For the large number of scatterers, according to Central Limit Theorem, ![]() is a deterministic process.
is a deterministic process. ![]() is a complex Gaussian process with a low-pass nonzero mean, and its envelop
is a complex Gaussian process with a low-pass nonzero mean, and its envelop ![]() consistent with Rayleigh distribution.
consistent with Rayleigh distribution.
In (6), ![]() is gain of satellite antenna p.
is gain of satellite antenna p. ![]() is angle that ground antenna l deviates from beam center p.
is angle that ground antenna l deviates from beam center p. ![]() is gain of ground antenna l. Generally, ground antenna is omnidirectional antenna, so
is gain of ground antenna l. Generally, ground antenna is omnidirectional antenna, so![]() .
.
In (7), ![]() is the nth multipath component random phase.
is the nth multipath component random phase. ![]() is carrier frequency. A (n) is the amplitude of multipath component which is influenced by the nth scatterer. Kpl represents sub-channel Rician Index from Tp to Rl,
is carrier frequency. A (n) is the amplitude of multipath component which is influenced by the nth scatterer. Kpl represents sub-channel Rician Index from Tp to Rl,![]() .
.
3. Multi-Beam Spatial Correlation Characteristics
3.1. Definition of Spatial Correlation
In the early stage of channel research, multi-antenna technology will get a huge channel capacity upgrade in the independent and identically distributed (iid) Rayleigh channel [5] [6], under the assumption that the interval between the antennas is large enough and the angle of arrival (AOA) angular spread is sufficiently large. However, in an actual mobile communication system, the angular spread of the received signal AOA is not large enough under the affection of the interval among antennas and scatterers distribution around. It results that the fading of received signal among different antennas and the signal received among the same antenna from different transmitting antenna are not statistically independent. So the correlation exists. This correlation is called by spatial correlation, its definition is written as
![]() (8)
(8)
where p and q are two transmitting antennas. l and m are two receiving antennas. hpl(t) represents channel response of antenna p to l. In the same way, hqm(t) represents channel response of antenna q to m. E[•] is expectation. ρpl,qm is correlation coefficient between received signal of antenna l and m.
3.2. Analysis of Multi-Beam Spatial Correlation
Since ![]() and
and ![]() are both zero-mean random process (
are both zero-mean random process (![]() ),
),![]() and
and ![]() are deterministic process, can be written as
are deterministic process, can be written as
![]() (9)
(9)
According to the model shown in Figure 3. The spatial correlation coefficient of direct-path component is
![]() (10)
(10)
where![]() , which is described the distance of transmitting antenna p and q.
, which is described the distance of transmitting antenna p and q. ![]() is the distance of receiving antenna m and l.
is the distance of receiving antenna m and l.
Also, the spatial correlation coefficient of multipath component is
![]() (11)
(11)
Since the large number of scatterers around ground receiver antennas (a larger number N), RS, HS and αR can replace the discrete variables RS(n), HS(n) and αR,n as an approximation. (11) can change into integral form
![]() (12)
(12)
RS, which is the distance of scatterer and ground receiver, can be described by hyperbolic distribution [4]. The height of scatterer HS, which PDF depends on environment around receiver, is normally described by normal distribution [7], Lon-normal distribution [8] etc. The normal distribution is used for modeling in this paper. In ground wireless communication system, the arrival angle of multipath signal is described by evenly distribution [9] or Laplace distribution. But in mobile satellite communication system, Laplace distribution is more suitable under testing in urban area [10], which is affected by the number and the distribution of scatterers around ground receiver.
When the arrival angle of received signal in x-y plane αR is Laplace distribution, the spatial correlation coefficient of multipath component in the received signal is shown as
![]() (13)
(13)
where![]() ,
, ![]() and
and ![]() are given by (14)
are given by (14)
![]() (14)
(14)
4. Numeric Results and Analysis
In this part, the channel spatial correlation coefficient of the signal received by ground antennas is obtained by numeric calculation in multi-beam satellite communication system, which adopt parabolic reflector antenna. All the parameters of simulation are given in Table 1, if not specified otherwise.
The calculation is on the assumption of![]() ,
, ![]() , which is the angle between component beam p to ground receiver and and carrier frequency is 2 GHz.
, which is the angle between component beam p to ground receiver and and carrier frequency is 2 GHz.
Figure 5 shows that in term of nT = 2, nR = 1, the relationship between ground spatial correlation coefficient among three Chinese cities, namely Mohe, Beijing and Shanghai, and the interval of satellite antennas.
As shown in Figure 5, with the increase of the antenna interval, spatial correlation coefficient among satellite channel showed a decreasing trend, and the higher the latitude, the slower decline.
Take Beijing as example, let K = 4 dB, Figure 6 shows the relationship among the interval of satellite antennas, ground antennas, and the spatial correlation
![]()
Figure 5. Relationship between the component beam correlation coefficient and the interval of satellite antennas.
![]()
Figure 6. Relationship among the interval of antennas and spatial correlation coefficient.
coefficient. With the interval increasing, spatial correlation coefficient showed a decreasing trend, but when the interval is small, the spatial correlation coefficient is still large.
5. Summary/Conclusion
In this paper, considering that the radio transmission feature and the antenna array feature the affection influence the spatial correlation coefficient, we create a 3-demension channel model. According to the model, we derive the spatial correlation coefficient among component beam which received by ground receiver with numeric calculation and analysis. The result shows that spatial correlation coefficient is still large even if the interval of antennas is small. Therefore, the spatial correlation coefficient cannot be ignored in satellite channel research.
Acknowledgements
This work is supported by the National Natural Science Foundation of China (No.61371073).