1. Introduction
Multiple-Input Multiple-Output (MIMO) technology is widely applied in modern communication system. It provides users with a higher data rate, better service quality and greater network capacity [1]. Compared to terrestrial communication system, satellite communication system has many advantages such as wide coverage, flexible connection, and little influence by topography, etc. It is widely used in the fields of transoceanic television broadcasting and telephone, communication in remote areas, maritime and aeronautical communication, navigation positioning and military communication. Because of the huge potential of MIMO technology to increase the system capacity, the application of MIMO technology in satellite communication system becomes a hot topic. In recent years, scholars have carried on a large amount of researches about satellite MIMO communication.
In 2005, P. R. King provided a model of distributed satellite MIMO channel [2], and then in second year, he completed a similar analysis and research on the polarized satellite MIMO channel, which shows the benefits of using MIMO in satellite communication [3]. Sellathurai also proposed a simplified statistical model of polarized satellite MIMO channel [4]. Benjamin Ros proposed a system scheme for interactive satellite MIMO communication using the OFDM system. He compared the performance of satellite MIMO system with multi-antenna SISO system under DVB-SH standard, and the results indicate that MIMO technology is necessary for satellite communication [5].
Compared with the abundant research results of satellite MIMO, the investigations about optimization of satellite MIMO system capacity are limited. How to improve the system capacity of satellite MIMO system is worthy of research and analysis. In this paper, we provide theoretical calculation of the system capacity of GEO and LEO satellite MIMO system, and then complete the optimization of system capacity. Especially for LEO satellites, we carry out the numerical analysis, which proves the correctness of the theory proposed in this paper.
2. System Model
Satellite system can be divided into GEO system and non-GEO system. Because the GEO system is relatively geostationary, MIMO system using GEO is more stable. The existing GEO systems are Inmarsat system and Thuraya system, but they both only have three satellites. The beam overlap area is not large enough since the number of satellites is too small. Thus, it is impossible to achieve MIMO system using multiple GEO satellites in most areas on the ground.
The orbit altitude of LEO satellite system is 700 to 1500 km, moving at a high speed relatively to the earth. Globalstar system and Iridium system are major existing LEO satellite communication systems until now, which respectively have 48 and 66 LEO satellites completing global coverage. The existing LEO satellites are abundant resources, and users can simultaneously connect multiple satellites in most areas of the Earth. Thus, there are enough LEO satellites to build MIMO system.
As shown in Figure 1, we consider a complete closed-loop scenario. The whole satellite MIMO system contains three components as follows.
Terrestrial transmitting terminal: The transmitter is generally a terrestrial station. It is mainly responsible for controlling, scheduling, and connecting the ground network and the user terminal in the entire communication process.
Communication satellite: Generally, there are two or more satellites, playing a role as relaying and forwarding in the whole communication system. The signal transmitted by the ground station is delivered to the user terminal through transparent forwarding or decode-and-forwarding.
User terminal: It could be hand-held mobile terminals, or terminals on-board, ship-borne and air-borne moving at a high speed, or even another fixed ground station.
General system includes two links: The uplink is from ground station to the satellite system and downlink is from satellite system to the user terminal. Maybe there also exist inter-satellite links among the satellites to assist communication.
In Figure 1, 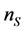 is the number of antenna of the ground transmitter,
is the number of antenna of the ground transmitter,  is the number of antennas of the relay satellite and
is the number of antennas of the relay satellite and  is the number of antenna of the receiver on the ground. In general,
is the number of antenna of the receiver on the ground. In general,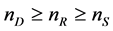 .
.
3. Capacity Analysis and Optimization
3.1. Capacity Analysis
In satellite communication systems, the satellite channel is significantly different from the terrestrial channel, because the power of its direct path is much greater than that of the multipath. For example, according to the data from ITU-R M.1225 [6], the power of direct path is about 20 dB greater than the maximum multipath. In fact, because the signal energy in NLOS channel signal is too small, the multipath signal has little effect on the capacity of the system compared with the existence of direct path [7]. Therefore, in this paper we only consider the influence of direct path.
In consideration of the free space propagation of the direct path through satellite-ground channel, the channel function can be expressed as [8]
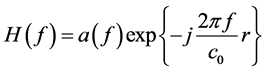 (1)
(1)
where r denotes the distance between the transmitter and the receiver,  denotes the signal amplitude attenuation when passing through the channel. Thus for 2*2 MIMO the capacity can be represented as
denotes the signal amplitude attenuation when passing through the channel. Thus for 2*2 MIMO the capacity can be represented as
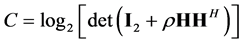 (2)
(2)
where 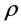 denotes the system SNR removing the channel fading part. The channel matrix H is expressed as
denotes the system SNR removing the channel fading part. The channel matrix H is expressed as
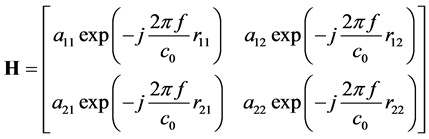 (3)
(3)
We establish an unified coordinate system to analyse and calculate the difference between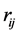 . It is shown in Figure 2 and Figure 3.
. It is shown in Figure 2 and Figure 3.
As shown in Figure 2, we define the equatorial plane as XOY plane, the polar direction as Z-axis. Besides, OX axis intersects 0 degrees’ east longitude and OY axis intersects 90 degrees’ east longitude. The two red circles in Figure 2 represent the location of ground terminal antennas. 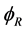 represents the latitude of ground terminals and
represents the latitude of ground terminals and  represents the longitude of ground terminals (East longitude is positive and West longitude is negative).
represents the longitude of ground terminals (East longitude is positive and West longitude is negative). 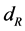 denotes the distance between two antennas on the ground, and
denotes the distance between two antennas on the ground, and 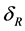 denotes the angle between two antennas and east direction. Then the coordinates of the two antennas on the ground are respectively expressed as
denotes the angle between two antennas and east direction. Then the coordinates of the two antennas on the ground are respectively expressed as
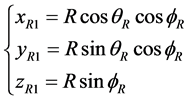 (4)
(4)
 (5)
(5)
Because the coordinates of two satellites are not necessarily related, we analyze a single satellite coordinates respectively. Satellite coordinate is shown in Figure 3.
The dotted line circle in Figure 3 is the orbit of satellite. A point is the ascending node (the intersection point of satellite orbit and the equatorial plane) of this orbit, . S is the satellite position.
. S is the satellite position. ![]() is the inclination angle of satellite orbit, which is a constant in one satellite system.
is the inclination angle of satellite orbit, which is a constant in one satellite system. ![]() is the phase of satellite orbit ascending node in XOY plane. In the same satellite system, the difference of
is the phase of satellite orbit ascending node in XOY plane. In the same satellite system, the difference of ![]() between each orbit is a fixed value.
between each orbit is a fixed value. ![]() changes in the angular velocity of
changes in the angular velocity of ![]() with the earth’s rotation, and
with the earth’s rotation, and ![]() is the angular velocity of the earth’s rotation.
is the angular velocity of the earth’s rotation. ![]() is the phase of satellite in its orbit. We define the phase of the ascending node A as 0˚, so
is the phase of satellite in its orbit. We define the phase of the ascending node A as 0˚, so
![]() (6)
(6)
![]() is the angular velocity of the satellite and
is the angular velocity of the satellite and ![]() is the initial phase of satellite in its orbit. Then the coordinates of the satellite can be expressed as
is the initial phase of satellite in its orbit. Then the coordinates of the satellite can be expressed as
![]() (7)
(7)
![]()
Figure 2. Terrestrial terminal coordinate.
where
![]() (8)
(8)
H is the orbit altitude of the satellite. Two satellites have different![]() . If the two satellites are in different orbit, they also have different
. If the two satellites are in different orbit, they also have different![]() .
. ![]() and
and ![]() both change with time.
both change with time. ![]() reflects the satellite motion in its orbit, and
reflects the satellite motion in its orbit, and ![]() reflects the movement of the earth’s rotation.
reflects the movement of the earth’s rotation.
3.2. Parameter Optimization of GEO System
Figure 4 is a schematic diagram of the GEO satellite MIMO coordinate. It is necessary to discuss the optimization of distance and angle between antennas, so that we can always keep the system capacity in the optimal value.
First, put Formula (3) into Formula (2). Capacity can be expressed as
![]() (9)
(9)
![]()
Figure 4. GEO satellite MIMO coordinate.
where ![]() is only related to
is only related to![]() , and it can be expressed as
, and it can be expressed as
![]() (10)
(10)
In order to maximize C, the following expression should be guaranteed
![]() (11)
(11)
In the GEO system, the satellite is fixed relatively to earth, and the rotation of the earth ![]() remains unchanged. Set
remains unchanged. Set![]() , and keep the satellite orbit plane parallel to the equatorial plane, as shown in Figure 4. Therefore,
, and keep the satellite orbit plane parallel to the equatorial plane, as shown in Figure 4. Therefore, ![]() , put it into Formula (7), we obtain
, put it into Formula (7), we obtain
![]() (12)
(12)
Put Formula (12) into Formula (4), we obtain
![]() (13)
(13)
Put Formula (12) into Formula (5), we obtain
![]() (14)
(14)
Let
![]() (15)
(15)
![]() (16)
(16)
![]() can be expressed as
can be expressed as
![]() (17)
(17)
Then by exploiting the small aqueous formula![]() , we obtain
, we obtain
![]() (8)
(8)
Put Formulas (14) and (18) into (11), it can be obtained that when place angle ![]() is fixed, the optimal value of
is fixed, the optimal value of ![]() is
is
![]() (19)
(19)
It can be seen that the optimal value of the terrestrial antenna is periodic variation. In the same way, let
![]() (20)
(20)
![]() (21)
(21)
Put Formula (20) and (21) into (19), It can be obtained that when ![]() is fixed, the optimal value of
is fixed, the optimal value of ![]() is
is
![]() (22)
(22)
3.3. Parameter Optimization of LEO System
In the LEO satellite system, there exists an angle between the satellite orbit plane and the equatorial plane, in addition, the angular velocity of satellites and the earth is different, so ![]() will change with time. Thus, it is necessary to discuss the optimization of
will change with time. Thus, it is necessary to discuss the optimization of ![]() and
and ![]() when time changes, so that we can always keep the system capacity in the optimal value.
when time changes, so that we can always keep the system capacity in the optimal value.
First, we calculate the distance ![]() and
and ![]() between two satellites and antenna No. 1 on the ground.
between two satellites and antenna No. 1 on the ground.
Let
![]() (23)
(23)
![]() (24)
(24)
Make use of Formulas (4) and (7). After simplification, we obtain
![]() (25)
(25)
Set the variable![]() ,
, ![]() can be represented as
can be represented as
![]() (26)
(26)
where
![]() (27)
(27)
Then by exploiting the small aqueous formula![]() , we obtain
, we obtain
![]() (28)
(28)
When place angle ![]() is fixed, the optimal value of
is fixed, the optimal value of ![]() is
is
![]() (29)
(29)
In this formula, it is obvious that the optimum value of ground antennas changes periodically. Similarly, let
![]() (30)
(30)
![]() (31)
(31)
When ![]() is fixed, it can be obtained that the
is fixed, it can be obtained that the ![]() corresponding largest system capacity can be expressed as
corresponding largest system capacity can be expressed as
![]() (32)
(32)
4. Numerical Analysis Results
Through the analysis above, it can be seen that optimum channel capacity of GEO and LEO satellite MIMO system is related to ![]() and
and![]() . Then numerical analysis is carried out to prove the correctness of the theory proposed in chapter III. Here we set LEO satellite system as an example of numerical calculation. For GEO satellite, results can be used in the same way.
. Then numerical analysis is carried out to prove the correctness of the theory proposed in chapter III. Here we set LEO satellite system as an example of numerical calculation. For GEO satellite, results can be used in the same way.
In order to calculate LEO satellite MIMO system through numerical analysis, orbit parameters of Globalstar system and Iridium system are needed. We also need to determine the system SNR ![]() besides of the orbit parameters of the two systems. SNR depends on satellite transmission power
besides of the orbit parameters of the two systems. SNR depends on satellite transmission power![]() , satellite antenna gain
, satellite antenna gain![]() , terrestrial antenna gain
, terrestrial antenna gain ![]() and received noise
and received noise ![]() of terrestrial antennas. These parameters are summarized in Table 1.
of terrestrial antennas. These parameters are summarized in Table 1.
System capacity of satellite MIMO system is closely related to the arrangement of ground antennas. The system capacity can be maintained at a optimal value by using tracking antenna chrtrolling ![]() and
and![]() . Figure 5 and Figure 6 show the performance of the tracking antenna using Formula (25). It can be seen that
. Figure 5 and Figure 6 show the performance of the tracking antenna using Formula (25). It can be seen that
![]()
Table 1. Main parameters in numerical analysis.
![]()
Figure 5. Tracking antenna performance (d = 0.2 m).
![]()
Figure 6. Tracking antenna performance (d = 2 m).
the system capacity of tracking antennas is significantly improved compared with the fixed antennas in both systems. The tracking antenna makes the system maintain a high and relatively fixed system capacity.
From Figure 5 and Figure 6, we can see the different capacity performance when the antenna spacing ![]() is 0.2 m and 2 m, when the antenna distance increases, we can find that the system capacity of the fixed antenna becomes more unstable with big fluctuation. It shows that tracking antenna is more significant for large-scale antenna system with larger antenna spacing.
is 0.2 m and 2 m, when the antenna distance increases, we can find that the system capacity of the fixed antenna becomes more unstable with big fluctuation. It shows that tracking antenna is more significant for large-scale antenna system with larger antenna spacing.
5. Conclusion
In this paper, we have analyzed the relationship between the capacity performance of satellite MIMO system and placement parameters of terrestrial antennas such the angle and distance. The numerical calculation verifies the possibility to optimize the parameters. Later, through formula derivation we obtain the time variation function of the optimal placement angle and distance of the ground antenna. Finally, numerical analysis is carried out according to the initial position of satellite in the practical system. The results demonstrate that the system capacity can be significantly improved when the antenna is traced using the theoretical analysis results.
Acknowledgements
This paper is supported by the National Natural Science Foundation of China # 61371073.