1. Introduction
Grey clustering assessment and analysis is an important part of grey system theory, which has been one of the most important techniques in the theory discussion and practical application. On the basis of the grey variable weight clustering method established by Professor Deng Julong [1] ; Professor Liu Sifeng proposed a grey fixed weight clustering evaluation method [2] [3] ; Grey optimal cluster model was established by Xiao Xinping [4] ; Xu Xiuli discussed the improvement measures of grey clustering analysis [5] ; The new grey clustering evaluation model based on the triangle whitenization weight function was also constructed by Professor Liu Sifeng [6] ; Mi Chuanmin put forward the entropy weight method to determine the weight of each index in grey cluster [7] ; Zhang Qishan discussed the measurement of characteristics of a grey cluster result [8] , the problem of grey cluster based on the hazy set is studied by Zhang [9] ; Grey interval clustering decision method was proposed by Luo Dang [10] . The above scholars studied from different aspects of grey clustering method and evaluation analysis. However, the above-mentioned various grey clustering analysis methods are based on the maximum principle of the clustering coefficient vector component to determine the grey clustering object’s grey classifications [11] . But in practical application, there are not distinguished differences of grey cluster coefficient. Dang Yaoguo put forward a new method of grey integrated clustering, which attempts to solve the problem of grey clustering that there are not distinguished differences of grey cluster coefficient [12] . In the integrated clustering method, the clustering object is divided into s classifications, and the value scope of the integrated clustering coefficient is divided into s disjoint equal length interval. In the grey clustering assessment, the grey integrated clustering method can solve the problem that there are not distinguished differences of grey cluster coefficient. However, there are some deficiencies in the division of the value scope of the integrated cluster coefficients [13] . This paper puts forward an improved method based on the existing problem, which is more accurate in distinguishing the grey classifications of grey clustering object, and the empirical analysis proves that the improved grey integrated clustering method is more valuable [14] .
2. Integrated Grey Clustering Method and Its Improvement
Definition 1 Assume that there are n clustering objects, m clustering indexes, s different grey classifications, observation value of clustering object i on the clustering index j is 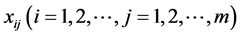 and the whitenization weight function of the i-th clustering object of clustering index j about k grey classification is
and the whitenization weight function of the i-th clustering object of clustering index j about k grey classification is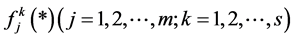 , the value of whitenization weight function of the i-th clustering object of clustering index j on k grey classification is
, the value of whitenization weight function of the i-th clustering object of clustering index j on k grey classification is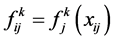 ,the whitenization weight function matrix about k grey classifications is
,the whitenization weight function matrix about k grey classifications is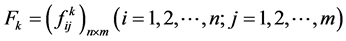 . Determine the grey clustering weight
. Determine the grey clustering weight 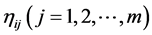 of each index. Generally, when there is no enough
of each index. Generally, when there is no enough
information, the weight can be set as 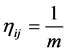 [15] .
[15] .
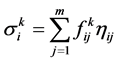 (1)
(1)
 (2)
(2)
where 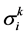 is clustering coefficient of clustering object i belongs to k grey classification,
is clustering coefficient of clustering object i belongs to k grey classification,  is called the clustering coefficient vector of the clustering object i.
is called the clustering coefficient vector of the clustering object i.
Definition 2 Order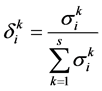 ,where
,where 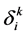 is represents normalized cluster-
is represents normalized cluster-
ing coefficient of the clustering object i belongs to k grey classification. Call Equation (3) as normalized clustering coefficient vector of clustering object i [16] .
 (3)
(3)
Definition 3 Assume that there are n clustering objects different grey classifications, order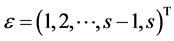 , Equation (4) is called the integrated clustering coefficient of clustering object i.
, Equation (4) is called the integrated clustering coefficient of clustering object i.
 (4)
(4)
Definition 4 Because of the integrated clustering coefficient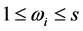 , the clustering object is divided into s classifications, and the range of the integrated clustering coefficient is divided into s disjoint equal length interval, as shown in Equation (5).
, the clustering object is divided into s classifications, and the range of the integrated clustering coefficient is divided into s disjoint equal length interval, as shown in Equation (5).
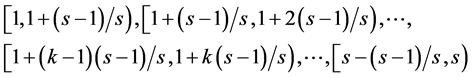 (5)
(5)
When there is no significant difference in the clustering coefficient of the i cluster and the integrated clustering coefficient of the object i is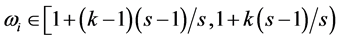 , we call the object i belongs to the k grey classification.
, we call the object i belongs to the k grey classification.
The accurate degree of integrated grey clustering evaluation coefficient is very important, and the grey degree of clustering coefficient is too big or too small may directly lead to the clustering objects belonging to different grey classification, in the definition 3![]() , integrated clustering coefficients
, integrated clustering coefficients ![]() of numerical and nature of the clustering coefficient exist error, this paper gives a new method, which the integrated clustering coefficients of accuracy is greatly improved, such as the definition 5 [17] .
of numerical and nature of the clustering coefficient exist error, this paper gives a new method, which the integrated clustering coefficients of accuracy is greatly improved, such as the definition 5 [17] .
Definition 5 Assume that there are n clustering object, s different grey classification, then![]() , Equation (6) is called integrated clustering coefficient of the clustering object i.
, Equation (6) is called integrated clustering coefficient of the clustering object i.
![]() (6)
(6)
Definition 6 The integrated clustering coefficient![]() , and the range of the integrated clustering coefficient is divided into s disjoint equal length interval, as shown in Equation (7).
, and the range of the integrated clustering coefficient is divided into s disjoint equal length interval, as shown in Equation (7).
![]() (7)
(7)
When there is no significant difference in the clustering coefficient of the clustering object i, If the integrated clustering coefficient of the object i is![]() , the object i belongs to the k grey classification [18] .
, the object i belongs to the k grey classification [18] .
This paper regards integrated clustering coefficients of ![]() and integrated clustering coefficients range median
and integrated clustering coefficients range median ![]() (such as:
(such as:![]() ) of similar degree
) of similar degree ![]() as the object i belong to k grey class of precision degree. Order
as the object i belong to k grey class of precision degree. Order![]() . In other words, the distance of integrated clustering coefficients
. In other words, the distance of integrated clustering coefficients ![]() and integrated clustering coefficients the center value
and integrated clustering coefficients the center value ![]() of the interval is closer ,the difference is smaller,
of the interval is closer ,the difference is smaller, ![]() is bigger, indicating the degree of i objects belong to k grey classification is stronger, this integrated clustering coefficients of numerical accuracy is higher; conversely,
is bigger, indicating the degree of i objects belong to k grey classification is stronger, this integrated clustering coefficients of numerical accuracy is higher; conversely, ![]() is smaller, indicating that the integrated clustering coefficients of numerical accuracy is poorer, the object i belongs to k grey classification is relatively weaker.
is smaller, indicating that the integrated clustering coefficients of numerical accuracy is poorer, the object i belongs to k grey classification is relatively weaker.
3. Empirical Analysis
The selection of mining method depends on coal mine geological structure and mining technological conditions. There is a wide variation between technical level of the selected mining method and the economic benefits, as the difference geological structure of coal mine or a coal mine in different lots. In order to improve the economic benefit of coal mining, which enterprises could select the appropriate mining method to achieve the economic benefit of coal enterprises best. How to make an objective and integrated evaluation of different mining methods. This paper selects original integrated clustering method and the improved integrated clustering method on different mining methods for analysis and evaluation. A coal mine uses four kinds of methods for coal mining: fully mechanized mining, top grade general mining, general mining and blasting mining ,which are regard as clustering objects, then this paper respectively takes the working face per unit area yield, mining effect, the equipment investment and the mining cost as the clustering index. According to the good, medium and poor three class classifications, the different indexes data of four different kinds of mining methods are shown in Table 1 [19] .
Through the investigation of the experts, the whitenization weight function ![]() of the j index about the k grey classification are [20] :
of the j index about the k grey classification are [20] :
![]()
According to the Delphli method, the weights of work surface area per unit area yield, mining efficiency, equipment investment and the cost are respectively as follows:![]() . Using the software to calculate the results of integrated clustering method and improved integrated clustering method, evaluating the influence degree of economic benefit of different coal mining method in this coal mine, then analyzing and comparing the
. Using the software to calculate the results of integrated clustering method and improved integrated clustering method, evaluating the influence degree of economic benefit of different coal mining method in this coal mine, then analyzing and comparing the
![]()
Table 1. The observation data of four different coal mining methods in coal mine.
accuracy of the integrated clustering coefficients calculated by the two methods, namely the grey degree of i to k. Specific results are shown in Tables 2-4.
It can be seen from Table 2 and Table 3 that the integrated clustering method and the improved integrated clustering method are less influence and the clustering results have no big changes in the economic benefit which brought by different coal mining method in macroscopic word. However, it can be seen from Table 4 that the accuracy of clustering coefficients of clustering object elevate from fully mechanized mining: 91.9%, top grade Mining: 89.6%, general mining: 94.5%, blasting mining: 90.3% to fully mechanized mining: 95.2%, top
![]()
Table 2. The improved integrated clustering method for the evaluation of different mining methods in coal mine.
![]()
Table 3. Integrated clustering method for evaluation and analysis of different mining methods in coal mine.
![]()
Table 4. The accuracy of the integrated clustering coefficient.
grade general Mining: 94.8%, general mining: 97.4%, blasting mining: 93.0%. The accuracy of improved integrated clustering coefficient is higher than the original integrated clustering coefficients. That is to say, the error of the improved method is smaller, the accuracy has been greatly improved, and also shows that the object i belongs to the k grey class. The improved method is obviously better than the original integrated clustering method.
Evaluation of the coal mine has not changed in the two methods, however, integrated clustering coefficients of improved integrated clustering method numerical error is smaller, and the degree of membership is more bright and strong [21] . Obviously, the improved clustering results are more in line with the actual, more real and effective, and provides more objective, science, truth, effective evaluation method for coal mining enterprises to take what kinds of mining method to improve economic benefits.
4. Conclusion
This paper makes some improvement about the original integrated clustering coefficient, further analyzes and improves the value interval of integrated clustering coefficient. The original integrated clustering coefficient ![]() is divided into s disjoint equal length interval, as shown in Equation (5). If the integrated clustering coefficient
is divided into s disjoint equal length interval, as shown in Equation (5). If the integrated clustering coefficient ![]() of the object i, then the object i belongs to k grey classification. The improved integrated clustering coefficient
of the object i, then the object i belongs to k grey classification. The improved integrated clustering coefficient ![]() is divided into s disjoint equal length interval, as shown in Equation (7). If the integrated clustering coefficient of object i
is divided into s disjoint equal length interval, as shown in Equation (7). If the integrated clustering coefficient of object i ![]() is k, then the object i belongs to k grey classification. The improved clustering result is more objective and reasonable, and the clustering coefficient is more accurate with small error, belonging to more distinct interval which conforms to objective facts. Finally, this paper takes four different coal-mining methods of a certain mine as examples, according to the influence of the different coal mining method of economic benefit of coal enterprises income, analyzes the four different kinds of mining methods category with improved integrated clustering method, shows the improved integrated clustering method more applicable and has better effectiveness.
is k, then the object i belongs to k grey classification. The improved clustering result is more objective and reasonable, and the clustering coefficient is more accurate with small error, belonging to more distinct interval which conforms to objective facts. Finally, this paper takes four different coal-mining methods of a certain mine as examples, according to the influence of the different coal mining method of economic benefit of coal enterprises income, analyzes the four different kinds of mining methods category with improved integrated clustering method, shows the improved integrated clustering method more applicable and has better effectiveness.
Acknowledgements
The authors are grateful to anonymous referees for their helpful and constructive comments on this paper. This work is supported by the soft-science foundation of Henan Province (172400410015) and the Philosophy and Social Science Foundation of Henan Province (2016BJJ022).