Active Power Allocation of Virtual Synchronous Generator Using Particle Swarm Optimization Approach ()
1. Introduction
Nowadays, because of growing concern in energy crisis and environmental issues, the penetration of renewable energy sources (e.g. photovoltaics and wind turbines) in power system is necessary and inevitable. Therefore, the concept of microgrid [1] is proposed to integrate various types of distributed generators (DGs).
The RES-based DGs integrated into microgrids are usually connected to the system by using an inverter. To control the inverter, several control methods could be implemented. The traditional method to control the inverter-based DGs is grid-connected current control. However, this kind of traditional control method has several limitations. Some of them are the inability to work in standalone mode and the lack of inertia that in effect, could slow the growth of RES penetration [2]. Therefore, to give the DGs the ability to work in standalone mode and also power-sharing ability, droop control was proposed [3]. Droop control is a control method to regulate real and reactive power using the concept similar to that used in synchronous generators for parallel operation of synchronous generators.
However, while the droop control could enhance the stability in microgrids by solving the issues arise when using the current control, the RES-based DGs controlled with droop control could not solve the issue of typically low inertia in microgrids. In microgrid with high penetration of inverter-based energy sources, the overall system inertia is low because the inverter does not have rotating mass to give the inertia support to the system. This may result in a poor response to voltage and frequency in case of large disturbance [4]. Therefore, a new control method which could add inertia virtually to the power system was conceptually proposed as virtual synchronous generator (VSG) [5], virtual synchronous machine (VISMA) [6], or synchronverter [7]. A brief explanation about different topologies of VSG is discussed in [8] and [9]. With proper energy management, virtual inertia control equipped in inverter-based DGs can give the DGs ability similar to kinetic energy reservoir in rotating mass of synchronous generator using the energy storage.
In applying virtual inertia control to the energy storage system of the RES- based DGs, one important aspect to be considered is the allocation of active power output from the VSG. When a large disturbance occurs, if the active power is not properly allocated, the final frequency might be exceeding the allowable limits. This paper proposes a method to determine active power allocation of VSG using particle swarm optimization (PSO). The method is used to set the active power allocation of VSG so that the microgrid can restore its frequency to allowable limits when a large disturbance occurs. In this paper, the considered disturbance is the separation of microgrid from the main power grid because of three-phase fault at the bus connecting the microgrid and main grid. The simulation results show that by properly allocating active power from VSG, the final frequency of the microgrid could be restored close to the nominal value when three-phase fault causing separation of microgrid from main grid occurs in the system. It is also shown that the utilization of VSG in frequency control could improve the dynamic stability of the system.
2. System Modeling
2.1. The Principle of VSG
The basic concept of VSG is shown in Figure 1 [5]. It consists of energy storage,
inverter, and a virtual inertia control mechanism to give the energy storage the inertia support capability. The energy storage is necessary to emulate the kinetic energy storage of the synchronous machine so that VSG can compensate the difference between input power of VSG and the measured output power from the grid [10].
Virtual inertia control is basically the representation of swing equation of the synchronous generator. The swing equation in virtual inertia control block including damping term in per-unit is given by the Equation (1) below
 (1)
(1)
where  and
and  are per-unit input power of VSG and measured output power from the grid, respectively, H is virtual inertia constant,
are per-unit input power of VSG and measured output power from the grid, respectively, H is virtual inertia constant,  is (
is ( ) in which
) in which 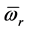 is per-unit virtual angular rotor speed and
is per-unit virtual angular rotor speed and 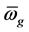 is per-unit angular rotor speed of measurement point, and
is per-unit angular rotor speed of measurement point, and  is per-unit virtual damping coefficient of the VSG. Using the virtual inertia control, RES-based DG could emulate the inertia support of a synchronous machine.
is per-unit virtual damping coefficient of the VSG. Using the virtual inertia control, RES-based DG could emulate the inertia support of a synchronous machine.
2.2. Virtual Inertia Control
The detailed control diagram of virtual inertia control is given in Figure 2 ([2] [10]). In this study, only active power control of VSG is considered in the virtual inertia control since the main focus is on the active power allocation of the VSG. Therefore Vpwm is set to a constant value of E0.
The “VSG Governor” in Figure 2 is an ω ? P droop controller ([2] [10]) and its block diagram is given in Figure 3. ω0 is the nominal angular frequency of the system, P0 is the set value of active power, and Kp is per-unit droop coefficient. The value of Kp is determined by 1/δ, where δ is speed regulation factor [10]. In this study, Kp is set as 20 pu., corresponding with the typical speed regulation factor δ of 5% in the droop control of a synchronous generator. All parameters in the block diagram are in per-unit to comply with per-unit notation in Equation (1).
2.3. Test System
The test system used in this study is similar to the one used in [11] and [12]. The
![]()
Figure 2. Control diagram of virtual inertia control.
system is shown in Figure 4. It consists of a group of feeders which could be a part of the distribution system. Load L1 and L4 are critical loads with the demand of 1.85 MW and 1.9 MW, respectively. Meanwhile, load L2, L3, and L5 are non-critical loads with the demand of 1.7 MW, 1.75 MW, and 2.4 MW, respectively. Under a normal operation, the system is connected to the utility grid. This system is typical of a real pilot microgrid project at Mae Hong Son Province in Thailand [13].
3. Allocation of Active Power of VSG Using Particle Swarm Optimization (PSO)
Particle swarm optimization (PSO) is a simple and robust optimization method initially proposed in [14]. It has been implemented successfully in various applications, e.g. design of PID controller in AVR system [15], reactive power and voltage control [16], etc. Some advantages of PSO are easy implementation, stable convergence characteristic, and good computational efficiency [15].
PSO can find the optimum solution of a parameter by searching it in the complicated search space based on the selected objective function and constraints. Using the best value of fitness obtained by each particle in the swarm in each of iteration, the best global fitness could be determined, and hence, the optimum value of the optimized parameter could also be determined. The basic algorithm of PSO is given in Equations (2) and (3)
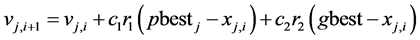 (2)
(2)
 (3)
(3)
where i is iteration,  is velocity of particle j,
is velocity of particle j, 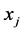 is position of particle j, c1 and c2 are individual and global learning rate, respectively, pbestj is the best position of particle j, gbest is the global best position, and r1, r2 are random number between 0 and 1.
is position of particle j, c1 and c2 are individual and global learning rate, respectively, pbestj is the best position of particle j, gbest is the global best position, and r1, r2 are random number between 0 and 1.
PSO is initiated by defining a group of random values called particles. Each
particle has its own position and velocity in the search space. During the iteration, the position and velocity of each particle are updated. The position of particle j that gives the best fitness is saved as pbestj, while the position among all particles that gives the best overall fitness is stored as gbest. The best optimized solution obtained is the value of gbest in the end of the iteration.
In this study, the number of particles Np is 10 with the number of iteration maxiter = 20. Learning rate c1 and c2 are both equal to 2. The inertia weight w is 0.729. Inertia weight is a factor multiplied to velocity  to enhance the performance of PSO [17]. The diagram of the proposed method to determine active power allocation of VSG using PSO is illustrated in Figure 5. The following steps are used in the proposed method:
to enhance the performance of PSO [17]. The diagram of the proposed method to determine active power allocation of VSG using PSO is illustrated in Figure 5. The following steps are used in the proposed method:
1) Define the objective function and the constraint of the parameters.
2) Initialize all parameters and start the iteration (i = 1).
3) Start the program for particle j = 1.
4) Execute the objective function for j-th particle and i-th iteration.
5) Update pbestj if the fitness of j-th particle is better than previous fitness (of the j-th particle). Update gbest only if the fitness of j-th particle is better than overall global fitness. Save the fitness value of j-th particle.
6) Check if all particles have been updated. If j is less than total particle Np, increase j by 1. Go back to step 4.
7) Increase iteration i by 1. If i + 1 ≤ maxiter, update position and velocity of each particle. Go back to step 2. maxiter is the defined maximum iteration.
8) If i + 1 > maxiter, the program ends. The best allocation of active power is defined by the value of gbest of the last iteration (i = maxiter).
In this study, PSO is used to determine the allocation of active power output from VSG so that the system can survive if a large disturbance causing separation of microgrid from the utility grid occurs in the system. PSO is used because it has good flexibility in its application. By carefully modifying the objective functions and the constraints, PSO can be used to obtain the optimum value in more complicated problem, i.e. finding the optimum value that fulfills the frequency requirement considering several different operating conditions (e.g. low load, heavy load, etc.).
![]()
Figure 5. The diagram for determination of active power allocation of VSG using PSO.
The objective function of the PSO used in this study is to minimize the deviation in the final frequency of microgrid in the case of occurrence of a large disturbance causing disconnection of the microgrid from the main system. In the considered system, there is no secondary control scheme in the system. Frequency is kept in the nominal value only by the utility grid. Therefore, proper allocation of active power output is necessary. The value obtained from the optimization is then used to set the value of P0 in Figure 2. The obtained value should also become one of the considerations in the planning stage to determine the capacity of the inverter.
The objective function of the PSO and its constraint is given by Equations (4) and (5), respectively. The constraint of the PSO is the active power rating of the VSG. The fitness parameter to be optimized is the system frequency.
![]() (4)
(4)
![]() (5)
(5)
4. Results and Discussion
During normal operation, the microgrid is connected to the main system. Loads in the microgrid are mainly supplied by DGs consist of hydropower generation and photovoltaic. When the DGs cannot supply all of the loads, the shortage of power is supplied by the utility grid. If a large disturbance occurs in the system, system frequency will deviate rapidly from its nominal value, resulting in the possibility of instability and system collapse. It is also the possibility of system instability because of the final frequency after the disturbance could not be restored to the allowable limits. In this study, VSG is used to stabilize the system during the disturbance. PSO is used to determine the allocation of active power of the VSG, so that system frequency could be restored to the allowable limit, thus avoiding system collapse.
In the performed simulations, the performance of the proposed method is tested by applying 3-phase fault at the bus connecting the microgrid and the utility grid at 10 s, causing the disconnection of microgrid from the utility grid. The fault is cleared in 100 ms. It changes microgrid operation mode from grid connected mode to islanding mode. The nominal frequency of the system is 50 Hz. The hydropower generator G1 in the microgrid have been equipped with the speed governor with the speed regulation factor of 5%.
The convergence rate of the objective function of PSO is shown in Figure 6. The graph shown is obtained from the optimization of the VSG. Figure 7 shows the active power allocation of VSG in each iteration. From these figures, it is shown that the proposed method converged after 15 iterations. Hence, the method is confirmed to give a convergent optimized value.
The active power allocation obtained using PSO is then compared with several other cases. The list of the tested configurations and their respective results are
![]()
Figure 6. Convergence rate of the objective function (VSG case).
shown in Table 1. The default active power allocation without optimization using PSO is 2.5 MW. This value is the middle value of the total capacity of the inverter.
The performance of the VSG and the effect of using PSO in determining its active power allocation can be seen in Figure 8. From Figure 8(a), compared with the default active power allocation of 2.5 MW, active power allocation using VSG can restore the system frequency to the nominal value. Based on the results, for the simulated operating condition, the VSG could give an acceptable value of frequency even without using the optimization. But, it might not be the case in other condition. In other operating condition, the frequency might fall outside the allowable limits and causing system instability.
The comparison in frequency response between VSG and inverter with current control for each configuration can also be analyzed. From the detailed view of Figure 8(b), it is shown that using conventional current control, there is large deviation of frequency from nominal value after the occurrence of the disturbance. The frequency is exceeding 50.5 Hz and in the case of without optimization, the frequency falls below 49 Hz during the transient. This is not the case in the microgrid in which VSG is utilized. If VSG is utilized in the microgrids, there is only small deviation in system frequency during transient when a large disturbance occurs.
![]()
Figure 7. Active power allocation of VSG in each iteration.
![]() (a)
(a)![]() (b)
(b)
Figure 8. System frequency after fault causing disconnection of the microgrid from main system (a) and its detailed view (b).
5. Conclusion
In this study, PSO is used to determine active power allocation of VSG to prevent the final frequency of microgrid to fall outside the allowable limits. Based on the simulation results, using active power allocation determined by the PSO, frequency of the system could be restored close to the nominal value of 50 Hz. While the frequency of the system is still acceptable in the case of VSG without PSO-based active power allocation, without proper allocation, the frequency might fall in a value outside the allowable limits in other operating conditions. From the simulation results, the proposed method also could be used to improve the frequency performance of inverter with conventional current control. However, the system utilizing inverter current control with power allocation determined by PSO has lower performance compared to a system utilizing VSG with PSO-based active power allocation.
It can also be concluded that virtual inertia control used in VSG has better performance compared with the conventional current control scheme. The maximum deviation of frequency during a large disturbance in microgrid utilizing VSG is significantly smaller than the deviation in the microgrid utilizing only the inverter with current control. Therefore, VSG could be used to improve the dynamic stability of the power system.