1. Introduction
Wave propagation is the phenomenon of energy transfer. Due to stress wave propagation the cracks are developed at the surface. To avoid the development of cracks on the surface of the material, the coating is provided on the material. Coating material is chosen with good tribological properties. The nature of contact between different components determines the state of stress which controls the fretting. The coating delays the crack initiation and retards the crack propagation. Paul [1] studied the radial vibrations of spheres of poroelastic material. Tajuddin [2] studied the torsional vibrations of finite composite poroelastic cylinders with two concentric cylindrical layers having a common curved surface and a solid composite poroelastic cylinder bonded end to end. Wisse et al. [3] presented the experimental results of guided wave modes in porous cylinders. Herbert Uberall [4] discussed the circumferential phase velocities for empty and fluid immersed spherical shells. Ahmed Shah and Tajuddin [5] studied the stress wave propagation in fluid filled poroelastic hollow spheres and made a comparison with stress wave propagation in empty poroelastic hollow spheres. Sharma et al. [6] studied three dimensional stress free vibrations of viscothermoelastic hollow sphere. They showed that toroidal motion gets decoupled from rest of the motion and remains unaffected to temperature variations along with some other particular cases. Shanker et al. [7] presented the analysis of poroelastic composite hollow spheres along with particular cases wherein rigid core and casing are considered.
In the present analysis, torsional vibrations of coated hollow poroelastic spheres are studied. The dilatations of solid and liquid media are zero, hence the liquid pressure developed in solid-liquid aggregate is zero so that the frequency equation of torsional vibrations is same both for a permeable and an impermeable surface. The frequency equation of a coated poroelastic solid sphere is obtained as a limiting case of coated poroelastic hollow sphere. The plots of frequency as a function of ratio of thickness of core to inner radius are presented for two types of coated hollow poroelastic spheres. There is increase in dispersion with the increase in thickness of the coating for the considered coated sphere. The torsional waves are non dispersive in thin coated poroelastic hollow sphere. The results of purely elastic solid are shown as a special case.
The study of torsional vibrations of elastic solid is important in several fields, e.g., soil mechanics, transmission of power through shafts with flange at the end as integral part of the shaft. It is now recognized that virtually no high-speed equipment can be properly designed without obtaining solution to what are essentially lateral or torsional vibration problems. Examples of torsional vibrations are vibrations in gear train and motor-pump shafts. Thus, from engineering point of view the study of torsional vibrations has greater interest. Such vibrations, for example, are used in delay lines. Further, based on reflections and refractions during the propagation of a pulse imperfection can be identified. This investigation is particularly applicable in Bio-Mechanics to identify and study the cracks in bones.
2. Governing Equations
The equations of motion of a poroelastic solid [8] in presence of dissipation (b) are
 (1)
(1)
where 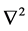 is the Laplace operator,
is the Laplace operator,  and
and  are displacements of solid and liquid respectively, e and Î are the dilatations of solid and liquid; A, N, Q, R are all poroelastic constants and
are displacements of solid and liquid respectively, e and Î are the dilatations of solid and liquid; A, N, Q, R are all poroelastic constants and  are the mass coefficients following [8] . The poroelastic constants A, N correspond to familiar Lame’s constants in purely elastic solid. The coefficient N represents the shear modulus of the solid. The coefficient R is a measure of the pressure required on the liquid to force a certain amount of the liquid into the aggregate while total volume remains constant. The coefficient Q represents the coupling between the volume change of the solid to that of liquid. The stresses
are the mass coefficients following [8] . The poroelastic constants A, N correspond to familiar Lame’s constants in purely elastic solid. The coefficient N represents the shear modulus of the solid. The coefficient R is a measure of the pressure required on the liquid to force a certain amount of the liquid into the aggregate while total volume remains constant. The coefficient Q represents the coupling between the volume change of the solid to that of liquid. The stresses  and the liquid pressure s of the poroelastic solid are
and the liquid pressure s of the poroelastic solid are
 (2)
(2)
where 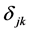 is the well-known Kronecker delta function and
is the well-known Kronecker delta function and 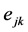 are the strain components of poroelastic solid.
are the strain components of poroelastic solid.
3. Solution of the Problem
Let (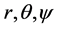 ) be spherical polar co-ordinates. Consider a coated (composite) hollow poroelastic sphere, in which the core (inner sphere) and the coating (outer sphere) each are homogeneous and isotropic. The inner radius of core is r1 and the outer radius of casing is r2 and also the interface lie at
) be spherical polar co-ordinates. Consider a coated (composite) hollow poroelastic sphere, in which the core (inner sphere) and the coating (outer sphere) each are homogeneous and isotropic. The inner radius of core is r1 and the outer radius of casing is r2 and also the interface lie at . The poroelastic hollow sphere of one material is bounded by and bonded to a spherical coating of different material. The physical parameters related to core are denoted by * as a super script. For example, the shear modulus of coating is N and the core is N*. The outer and inner surfaces of the coated poroelastic sphere are free from stress and at the interface, the stresses and displacements are continuous. For torsional vibrations, the only non-zero displacement components of the solid and liquid media are
. The poroelastic hollow sphere of one material is bounded by and bonded to a spherical coating of different material. The physical parameters related to core are denoted by * as a super script. For example, the shear modulus of coating is N and the core is N*. The outer and inner surfaces of the coated poroelastic sphere are free from stress and at the interface, the stresses and displacements are continuous. For torsional vibrations, the only non-zero displacement components of the solid and liquid media are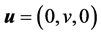 ,
, 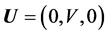 respectively. These displacements are functions of
respectively. These displacements are functions of  and time
and time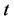 . When
. When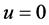 ,
, 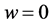 and
and 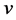 is a function of
is a function of ![]() and time
and time![]() , the equations of motion (1) in spherical polar form reduces to
, the equations of motion (1) in spherical polar form reduces to
![]() (3)
(3)
where![]() .
.
Let the propagation mode shapes of solid and liquid ![]() and
and ![]() are
are
![]() (4)
(4)
here ![]() is the frequency of wave and
is the frequency of wave and ![]() is complex unity or
is complex unity or![]() . Substitution of Equation (4) in Equation (3) results in
. Substitution of Equation (4) in Equation (3) results in
![]() (5)
(5)
where
![]() (6)
(6)
The second equation of (5) gives
![]() (7)
(7)
Using Equation (7) into first equation of (5), we obtain
![]() (8)
(8)
where ![]() and
and ![]() are
are
![]() (9)
(9)
In Equation (9), ![]() is shear wave velocity [8] and
is shear wave velocity [8] and![]() ,
, ![]() ,
, ![]() are defined in Equation (6). Equation (8) is an equation that can be reduced to Bessel’s differential equation of fractional order. Hence the solution of Equation (8) is
are defined in Equation (6). Equation (8) is an equation that can be reduced to Bessel’s differential equation of fractional order. Hence the solution of Equation (8) is
![]() (10)
(10)
where ![]() and
and ![]() are constants and
are constants and![]() ,
, ![]() are Spherical Bessel functions of first and second kind respectively (
are Spherical Bessel functions of first and second kind respectively (![]() is the order of spherical harmonic).
is the order of spherical harmonic).
Thus the displacement of solid is
![]() (11)
(11)
From Equation (4), it can be seen that the normal strains![]() ,
, ![]() and
and ![]() are all zero. Therefore the dilatations of solid and liquid media each is zero. Hence the liquid pressure s developed in solid-liquid aggregate following Equation (2) is identically zero. Accordingly for torsional vibrations no distinction between a permeable and an impermeable surface is made. Considering the boundary to be stress free, the frequency equation obtained for torsional vibrations is same for both permeable and impermeable surfaces. When
are all zero. Therefore the dilatations of solid and liquid media each is zero. Hence the liquid pressure s developed in solid-liquid aggregate following Equation (2) is identically zero. Accordingly for torsional vibrations no distinction between a permeable and an impermeable surface is made. Considering the boundary to be stress free, the frequency equation obtained for torsional vibrations is same for both permeable and impermeable surfaces. When![]() ,
, ![]() and
and ![]() is a function of
is a function of ![]() and time
and time![]() , the only non-zero stress
, the only non-zero stress ![]() for solid is
for solid is
![]() (12)
(12)
The stresses and displacements of solid for the outer spherical shell (coating) and inner spherical shell (core) are
![]() (13)
(13)
where the elements ![]() are
are
![]() (14)
(14)
4. Frequency Equation
Outer and inner surfaces of the coated hollow poroelastic sphere are assumed to free from stress and at the interface, the stresses and displacements are continuous. Thus the boundary conditions for the considered problem are
![]() (15)
(15)
Since the considered vibrations are shear vibrations, the dilatations of solid and liquid media each is zero, thereby liquid pressures in outer and inner poroelastic spherical shells ![]() and
and ![]() developed in solid-liquid aggregate will be identically zero and no distinction between pervious and impervious surface is made. Thus by using the boundary conditions (15) and eliminating the constants C1, C2, D1, D2 we get the frequency equation
developed in solid-liquid aggregate will be identically zero and no distinction between pervious and impervious surface is made. Thus by using the boundary conditions (15) and eliminating the constants C1, C2, D1, D2 we get the frequency equation
![]() (16)
(16)
In Equation (16), the elements ![]() are defined in Equation (14).
are defined in Equation (14).
Now we consider two particular cases of the frequency Equation (16) in the following:
(i) When inner radius of core approaches to zero, the considered problem reduces to the problem of torsional wave propagation in solid coated poroelastic sphere. In this case, the frequency Equation (16) under suitable boundary conditions reduce to
![]() (17)
(17)
where the elements ![]() are defined in Equation (14).
are defined in Equation (14).
(ii) When the poroelastic material of the core vanishes, the considered problem reduces to the problem of torsional wave propagation in hollow poroelastic sphere and the frequency Equation (16) or (17) under suitable boundary conditions, reduce to
![]() (18)
(18)
By using the following relations [9]
![]() (19)
(19)
Equation (18) is simplified to the form [Equation (17), Bulletin of Calcutta Mathematical Society, Volume.103, pp.161-170] presented in and studied by Ahmed Shah and Tajuddin [10] .
5. Normalization of Frequency Equation
For the purpose of analysis of the frequency Equation (16), we consider a non- dissipative medium where b = 0. It is convenient to introduce the following non- dimensional variables:
![]() (20)
(20)
where![]() . Also
. Also ![]() and
and ![]() are reference velocities (
are reference velocities (![]() ,
,![]() ) with
) with![]() . The non dimensional form of frequency Equation (16) with the help of Equation (20) consists of non- dimensional frequency as a function of
. The non dimensional form of frequency Equation (16) with the help of Equation (20) consists of non- dimensional frequency as a function of ![]() and
and![]() . Coated poroelastic hollow spheres with thin, moderately thick and thick coating are considered. Parameters of two types of coated poroelastic hollow spheres are used to compute the frequency as a function of ratio of thickness of core to inner radius. These coated poroelastic hollow spheres are designated as “coated sphere-I” and “coated sphere-II”. Poroelastic hollow sphere made of water saturated sandstone [11] is coated with sandstone saturated with kerosene [12] and this coated poroelastic sphere is designated as coated sphere-I. Poroelastic hollow sphere made of kerosene saturated sandstone is coated by sandstone saturated with water and this coated poroelastic sphere is designated as coated sphere-II. The non-dimen- sionalised physical parameters of these coated poroelastic spheres are given below:
. Coated poroelastic hollow spheres with thin, moderately thick and thick coating are considered. Parameters of two types of coated poroelastic hollow spheres are used to compute the frequency as a function of ratio of thickness of core to inner radius. These coated poroelastic hollow spheres are designated as “coated sphere-I” and “coated sphere-II”. Poroelastic hollow sphere made of water saturated sandstone [11] is coated with sandstone saturated with kerosene [12] and this coated poroelastic sphere is designated as coated sphere-I. Poroelastic hollow sphere made of kerosene saturated sandstone is coated by sandstone saturated with water and this coated poroelastic sphere is designated as coated sphere-II. The non-dimen- sionalised physical parameters of these coated poroelastic spheres are given below:
![]()
6. Numerical Results and Discussion
Frequency equation of coated poroelastic spheres (16) is non-dimensionalised. For a given poroelastic material, Equation (16) constitutes a relation between non-dimensional frequency and ratio of thickness of core to inner radius for fixed values of![]() . Different values of g2, viz., 1.1, 1.5 and 3.0 are taken for numerical computation. These values of
. Different values of g2, viz., 1.1, 1.5 and 3.0 are taken for numerical computation. These values of ![]() represent thin coating, moderately thick coating and thick coating respectively. Since stress wave propagation is the phenomenon of energy transfer, hence it plays a major role in fretting.
represent thin coating, moderately thick coating and thick coating respectively. Since stress wave propagation is the phenomenon of energy transfer, hence it plays a major role in fretting.
The phase frequency first three modes of coated poroelastic spheres-I and II are presented in Figure 1 for thin coating. From Figure 1 it is clear that the frequency of coated poroelastic sphere-I is less than that of coated poroelastic sphere-II when![]() . Then beyond
. Then beyond![]() , the frequency of poroelastic sphere-II is less than that of the sphere-I. The first three modes in coated sphere-I and II are non-dispersive; and the frequency is almost constant or there is a small variation.
, the frequency of poroelastic sphere-II is less than that of the sphere-I. The first three modes in coated sphere-I and II are non-dispersive; and the frequency is almost constant or there is a small variation.
Figure 2 shows the frequency of moderately thick coated spheres-I and II where we see that the frequency of coated sphere-I is more than coated sphere-II for each of the first three modes in ![]() and beyond
and beyond![]() ,, the frequency of coated sphere-II is more than that of coated sphere-I. Also we see that the first three modes in coated sphere-II are non-dispersive while these are dispersive in coated sphere-I. The frequencies of thick coated sphere-I and II are presented in Figure 3 and here we see that the first three modes in coated
,, the frequency of coated sphere-II is more than that of coated sphere-I. Also we see that the first three modes in coated sphere-II are non-dispersive while these are dispersive in coated sphere-I. The frequencies of thick coated sphere-I and II are presented in Figure 3 and here we see that the first three modes in coated
![]()
Figure 1. Frequency as a function of h/r1 (Thin Coating).
![]()
Figure 2. Frequency as a function of h/r1 (Moderately Thick Coating).
![]()
Figure 3. Frequency as a function of h/r1 (Thick Coating).
sphere-I and II are dispersive. Hence it can be concluded that modes are non dispersive in thin coated spheres and as the thickness increases, the modes become dispersive. We also see there is increase in the frequency with the increase in thickness of the coating.