1. Introduction
One of the most fundamental questions of modern interdisciplinary science is what information is. This question puts a bridge over many different scientific disciplines such as information theory, physics, biology, linguistics to name a few. Thus the modern understanding of the information assumes any piece of information to be representable into a sequence of binary digits. Accordingly the human brain is also supposed to perceive the corresponding environmental influence as a sequence of binary digits. Then, the intelligence is supposed to be executed as a universal Turing machine. It is believed also that the whole knowledge about the Universe is admissible and obtainable by recursive means only. In turn, the later makes each and every partial law algorithmically reachable from any other. Hence this lays grounds for Universal law whose major property is that all partial laws are its algorithmic derivatives. The fundamental flaw of this setting is that the absolute law would comprise simultaneously both a partial law and its negation. Let me clarify this flaw by an example which comes from the field of emergent phenomena namely from the Belousov-Zhabotinsky reaction. It is well-known that when concentrations of reagents reach certain values, an initially homogeneous solution starts producing waves and patterns which stay as long as the concentrations are kept at those values. However, the emergence of waves and patterns implies violation of the Second Law viewed in its most widespread formulation which asserts that the equilibrium state is the state of maximum entropy and that the equilibrium is a global attractor for all initial states. In this case it implies that equilibrium is the homogeneous solution and once reached, the system stays there forever. As a result, our universal law should comprise both the Second Law and its violation in a single specific law.
Another flaw of the still dominant traditional concept of information is that neither process of its obtaining is in balance with the environment. Let me explain the latter statement by the following consideration.
It is generally accepted that the price for obtaining any piece of information is certain dissipation of heat into non-information degrees of freedom. This statement, known as Landauer principle, yields an uncontrolled heating of the environment since the hardware is supposed to be able to execute any algorithm. As a result, no hardware is in balance with its environment unless special precautions are taken. The overheating is the fact even in the case when the non-in- formational degrees of freedom form a heat bath, since it is impossible apriori to judge whether a given algorithm halts. Thus, obtaining information is rather a kind of destructive measurement: the information is gained at the expense of inducing changes both in a system and its environment which eventually renders the obtained information always out-of-date. Moreover there is no general rule for simultaneous optimization among computational costs, quality of information and long-term balance with environment.
The fundamental value of the Landauer principle is that it relates information and heat: two very distinct in their origin notions. Indeed, while the information is supposed to be purely mathematical notion, the notion of heat originates from physics. Therefore, the information obtains a physical feature through rendering the price of each bit to be expressed by a specific amount of heat.
The above considerations give rise to the following dilemma: is there any way of resolving the problem of overheating in the above considered conceptual framework or one should go for a completely novel paradigm about information and its relations with physics and the other scientific disciplines? This paper considers some reasons why one should adopt the second alternative, namely adopting a new paradigm about information and its relations with physics and the other scientific disciplines. In my recent book [1] I have introduced and systematically developed a new paradigm for explaining the behavior of complex systems. There I have introduced a novel understanding of the information. In Section 3 I will present a brief introduction to that approach. One of the tasks of the present paper is to prove that in the setting of boundedness the corresponding processing of information is always in balance with the environment. The most non-trivial and unexpected effect of this result is that it always comes along with the ban over gaining information from fluctuations alone. The major focus of the present paper is to demonstrate that the problem about energetic prices of a piece of information is a key part of the question about whether information can be created from fluctuations alone. A ban over gaining information from fluctuations alone constitutes the notion of the ban over information perpetuum mobile stated in the title of the present paper. The major value of these considerations is the proof that the ban over information perpetuum mobile is model independent, i.e. it is impossible to acquire information from fluctuations alone both in the frame of the traditional and in the frame of the novel approach. Yet, the model independence of the ban over information perpetuum mobile constitutes the major difference between the traditional approach and the recently introduced concept of boundedness to be: while the traditional computing is never in balance with the environment unless special precautions are taken, the computing grounded on the concept of boundedness is always in balance with non- specified ever-changing environment.
2. Landauer Principle and Maxwell Demon
The goal of this section is to demonstrate that the Landauer principle is a consequence of model dependence related to the abilities of the Maxwell demon. I start the section with a brief reminder about the basic characteristics of Maxwell demon and the Landauer principle. The latter is considered as an implement for keeping the Second Law valid from its violation by the demon.
Maxwell demon was introduced by the famous Scottish physicist J. Maxwell in order to demonstrate the statistical nature of the Second Law. The demon is a super-minded tiny creature that opens unidirectionally a frictionless door between two chambers full of equal amount of gas each time when it is approached by a molecule whose velocity is greater than the average one. In result one of the chambers turns hotter than the other one which launches exertion of useful work without any dissipation of heat. The latter, however, is in severe contradiction with the Second Law which does not allow execution of useful work without certain dissipation of heat. Put it in other words, by means of demon’s super-intelligence it would be possible to obtain information out of fluctuations alone thus violating the Second law.
A lot of attempts have been made to reconcile the demon with the Second Law. The Landauer principle is one of the most successful ones in this direction [2] - [8] . It says that the demon and the chambers of gas form a closed system and thus to complete a cycle of work it is necessary to erase the information gained during the cycle from the demon’s mind. The erasure is implemented by dissipation of certain amount of heat in the non-information degrees of freedom. The overheating does not happen because it is assumed that the non-information degrees of freedom play the role of a heat bath. To remind that the latter implies no changes in the temperature of the heat bath have to happen during its interaction with the system under consideration.
Since its introduction, heated non-stoppable debates with a lot of arguments for and against Landauer principle have been current in the scientific and the philosophical literature. Yet, the subject-matter not discussed so far is the question about the kind of demon’s intelligence. On the one hand its intelligence is of human nature since it can read the velocity of the molecules and it accepts the above model as a true one. On the other hand it operates as a computer that stores operational information in a special for this purpose register. It is that register that the stored information is erased from after completing a cycle.
I will prove that the demon’s intellectual super-capacity is model dependent. It happens because the statistical distribution of the magnitude of velocity (Maxwell distribution) turns corrupted because the average velocity is not robust to coarse-graining. Let me start with the very notion of average velocity: by definition it is given by the following expression:
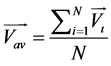 (1)
(1)
where 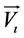 is the velocity of the i-th molecule; N is the number of the molecules in a chamber. Under the major statistical assumption that the velocities of different molecules are independent from one another, it is postulated that the averaged over large number of molecules velocity obeys time-translational invariance in thermodynamic equilibrium. In turn, the time-translational invariance of the average velocity renders the velocities of the molecules to obey statistical distribution (Maxwell distribution). However, the latter postulate is controversial since the time-translational invariance is corrupted by the process of coarse- graining. To remind: the process of coarse-graining implies averaging over a partitioned system where partitioning implies dividing of a system into cells of arbitrary size and averaging within each and every cell. The statement is that the averaging would be insensitive to the way partitioning is made which in turn would provide that the averaged variable obeys time-translational invariance. However, under the assumption of about the statistical independence of the molecules, the magnitude and the direction of averaged over a cell velocity vary wildly from one cell to another because the statistical independence of molecules renders the margins of variations within cells to be proportional to the largest velocity involved into a cell. Taking into account that the largest possible velocity varies from zero or infinity due to statistical independence of the molecules, it is obvious that the notion of average velocity becomes ill-defined because there is no uniform convergence of the average velocity to any value under the operation of coarse-graining. The deviations from the mean are of the order of the velocity itself which renders the time-translational invariance of the average velocity impossible. The above obtained result strongly undermines the Maxwell distribution of the magnitude of the velocities because the lack of uniform convergence of the average velocity under coarse-graining makes the distribution of the velocities sensitive to the number of the molecules in each and every cell. This result is incompatible with the requirement that statistical distributions are to be independent from the number of species involved in their derivations. It is worth reminding that this independence would provide grounds for the thermodynamic limit for all quantities calculated by its means. To remind, the thermodynamic limit implies that the thermodynamic properties of every system are independent from the size of the system.
is the velocity of the i-th molecule; N is the number of the molecules in a chamber. Under the major statistical assumption that the velocities of different molecules are independent from one another, it is postulated that the averaged over large number of molecules velocity obeys time-translational invariance in thermodynamic equilibrium. In turn, the time-translational invariance of the average velocity renders the velocities of the molecules to obey statistical distribution (Maxwell distribution). However, the latter postulate is controversial since the time-translational invariance is corrupted by the process of coarse- graining. To remind: the process of coarse-graining implies averaging over a partitioned system where partitioning implies dividing of a system into cells of arbitrary size and averaging within each and every cell. The statement is that the averaging would be insensitive to the way partitioning is made which in turn would provide that the averaged variable obeys time-translational invariance. However, under the assumption of about the statistical independence of the molecules, the magnitude and the direction of averaged over a cell velocity vary wildly from one cell to another because the statistical independence of molecules renders the margins of variations within cells to be proportional to the largest velocity involved into a cell. Taking into account that the largest possible velocity varies from zero or infinity due to statistical independence of the molecules, it is obvious that the notion of average velocity becomes ill-defined because there is no uniform convergence of the average velocity to any value under the operation of coarse-graining. The deviations from the mean are of the order of the velocity itself which renders the time-translational invariance of the average velocity impossible. The above obtained result strongly undermines the Maxwell distribution of the magnitude of the velocities because the lack of uniform convergence of the average velocity under coarse-graining makes the distribution of the velocities sensitive to the number of the molecules in each and every cell. This result is incompatible with the requirement that statistical distributions are to be independent from the number of species involved in their derivations. It is worth reminding that this independence would provide grounds for the thermodynamic limit for all quantities calculated by its means. To remind, the thermodynamic limit implies that the thermodynamic properties of every system are independent from the size of the system.
A very important characteristic which crucially depends on the uniform convergence of the average velocity and its robustness to coarse-graining is temperature. According to the statistical theory the temperature is proportional to the magnitude of the average velocity and it is supposed to be an intensive variable, i.e. to be independent from the size of a system. However, the latter is impossible under the above considered conflict between the time-translational invariance of the averaged velocity and the statistical independence of the velocities and positions of different molecules.
Therefore, following this setting, the demon can be deceived by misjudging current average velocity in any neighborhood of any chamber and in result she/he can select a molecule of lower velocity compared to the others. Moreover, even if she/he selects a molecule of larger velocity it does not necessarily imply “heating up” of the corresponding chamber since the temperature is still ill-de- fined. In turn this proves that demon’s intelligence is model-dependent. No reconciliation of this paradox is ever possible because of the incompatibility of the requirements: 1) the magnitude of the velocities obeys statistical distribution (Maxwell distribution); 2) the velocities of different molecules are independent from one another. In result, the information that the demon obtains is almost always wrong.
Outlining, deception of Maxwell demon is a generic for the traditional approach property. Indeed, the number of configurations where a single cell has specific properties (smaller/larger velocity of the participating molecules nearest to the door) has a zero measure. In turn the latter renders the deception of the demon generic property. Thus, in the frame of the traditional statistical approach the generic deception of super-intelligent Maxwell demon renders executing of useful work, i.e. obtaining information out of fluctuations alone impossible.
Then we face the fundamental question whether there is a type of intelligence where it is possible to create information out of fluctuations alone and will the demon be deceived again?!
3. Boundedness and Self-Organized Semantics
Posed in another way the above presented question is whether the above discussed model dependence of the demon’s intelligence is exclusive for the traditional statistical approach alone or it has a broader understanding in the sense that it is generic for another type of intelligence as well. In order to find out which alternative to follow, let me consider the same problem but exploring the case when the demon retains another type of intelligence. In [1] I have put forward a novel notion of intelligence whose major property is an autonomous creation and comprehension of information. Crucial advantage of such notion is the wide scope of its relevance: it is relevant not only in the case of Maxwell demon but it opens the door to a new type of intelligence which, though being fundamentally different from a Turing machine, is its counterpart.
In the present section I outline the exclusive properties of the new type of intelligence. The proof that the Maxwell demon is unable to utilize fluctuations alone for acquiring information is presented in the next section.
The notion of information which I have put forward in [1] is grounded on the understanding that the response of a complex system to any environmental impact is local, yet bounded in the sense that neither the amplitude nor the rate of exchange of energy/matter/information exceed specific for a system margins. In turn, this makes the response non-linear and what is more important and new, non-homogeneous both in the time and in the space. It is worth noting that by definition non-homogeneity implies local adaptability of the corresponding rules of response so that to fit margins of boundedness of rates and amplitudes. An exclusive for the boundedness property of each and every system’s response is that the latter decouples in two interrelated parts which are robust to the statistics of the environmental changes: a specific for a system self-organized homeostatic pattern and a noise term with certain universal properties. The robustness of the homeostatic pattern to the environmental changes makes it appropriate candidate for a definition of information symbol. An exclusive for that decomposition property is that it persists independently of the statistical properties of the environmental variations and internal fluctuations. In turn, this robustness provides autonomy for the corresponding notion of information symbol in an ever-changing environment. Yet, what makes such definition unique in a kind is the presence of a non-recursive component additional to the characteristics of a homeostatic pattern. The non-recursive component commences from the highly non-trivial interplay between the “homeostatic” and the “noise” terms in the equation-of-state which governs the evolution of a system. The fundamental importance of the non-recursive component is that its presence renders algorithmic uniqueness of every homeostatic pattern. It is worth noting that the presence of a non-recursive component at finite distance from the homeostatic pattern and noise band is an exclusive property of bounded noise only; for unbounded noise any such component, if exists, is shifted to infinity.
The ubiquitous presence of non-recursive component in the definition of an information symbol renders algorithmic uniqueness of each and every partial laws of Nature and thus puts a ban over existence of a single universal law of Nature such that all partial laws are its algorithmic derivatives. This constitutes fundamental difference with the traditional algorithmic approach where all partial laws are expressed in recursive means only and thus each partial law is algorithmically reachable from any other and each of them is a specific algorithmic derivative of a Universal law.
The crucial step forward introduced in [1] [9] is the notion of semantic-like intelligence executed by means of a response organized into cycles of non-me- chanical engines “built” by passing through several homeostatic patterns each of which characterizes a different state of a system. The boundedness of the rates sets the states through which any given cycle passes as the only adjacent ones. In turn, this property implements the autonomy of the response: the cycle follows through adjacent states only irrespectively to the intensity of the current environmental impact. Then, the autonomy of response is the physical implementation of the ability for autonomous creation and comprehension of information.
The performance of non-mechanical engines does not support validity of the laws of arithmetic. Indeed, it is obvious that neither associative, nor distributive nor commutative law holds at the performance of any engine. In turn, this opens the door to a new type of computing which is fundamentally different from the traditional one. Note that the traditional computing is grounded on the view that all the laws of Nature are executable by recursive means only and thus each and every of them is algorithmically reducible to a specific sequence of arithmetic operations.
It is worth noting that the execution of the response through a specific sequence of non-mechanical engines renders it to acquire the fundamental for any piece of semantics property that is the property of sensitivity to permutations. This property is physically implemented by each and every non-mechanical engine: indeed, like a Carnot engine which in one direction works as a refrigerator and in the other one as a pump, its performance explicitly depend on the direction of its operation.
It is proven in [1] that the efficiency of non-mechanical engines does not take over the efficiency of the corresponding Carnot engine. Thus, both creation and comprehension of information has its price: now the price is not only dissipation of heat but it also involves functional rearrangements of a system since changes of homeostasis are necessary ingredient for execution of any cycle. A major move ahead is association of the notion of homeostatic pattern with the notion of information symbol on the one hand and association of the notion of semantic unit with the operation of the corresponding non-mechanical engine on the other hand. Then, on the phenomenological level, the robustness of homeostatic patterns to the environmental variations justifies that it is impossible to acquire information out of noise alone. It is worth noting once again that any piece of semantics requires changes of homeostasis.
It should be stressed that though according to its definition an information symbol always comprises both a homeostatic pattern and the corresponding non-recursive component, the specific information is concentrated in the homeostatic pattern. The presence of non-recursive component in the notion of information symbol constitutes the algorithmic non-reachability of information symbols from one another.
My further task is the demonstration that the ban over information perpetuum mobile is constituted on the microscopic level. The non-triviality of the corresponding analysis lays in the observation that though average velocity of the species turns out to be well-defined in the frame of the concept of boundedness, the demon is deceived again.
In order to make the transition from phenomenological to microscopic level plausible let me consider the issue about how the notion of average velocity and temperature enter the notion of homeostatic pattern.
An exclusive for the boundedness property is that the semantic-like response of a system is organized in a multi-level non-extensive hierarchy similarly to the hierarchy of the semantics of human languages. Indeed, the words are created out of letters, sentences out of words, paragraphs out of sentences etc. This property commences from the two-fold presentation of information: on the one hand each semantic symbol is represented by the corresponding letters; on the other hand the meaning of a semantic unit is represented by the performance of the corresponding non-mechanical engine. An exclusive property of every semantic unit is its algorithmic irreducibility to the letters it consists of since the latter comprise specific non-recursive components in their characteristics. In turn this irreducibility opens the door to a non-extensive hierarchy of the response similar to that of human languages.
Crucial for that hierarchy property is that the inter-level feedbacks appear as a “noise” terms in the corresponding equations-of-state. This poses the question about the role of the inter-level feedbacks in the creation and comprehension of information. This constitutes one of the tasks of the present paper.
The role of inter-level feedbacks is three-fold: 1) they give rise to a non-recur- sive component in the characteristic of each and every homeostatic pattern and thus it provides its algorithmic uniqueness; 2) they participate in constituting the best survival strategy in an ever-changing environment. This task is considered in my recent paper [10] ; 3) the inter-level feedbacks maintain the temperature and concentration to be well-defined intensive variables. This issue has been considered in my recent paper [11] . Because of its relevance to the present paper I will represent some of considerations made in [11] again. Thus, in the next section I shall prove that the temperature and concentration are characteristics of the homeostasis and so they are robust to the details of the inter-level feedbacks.
It is worth noting the far going consequences of that proof. They consist of the fact that the velocities of the molecules in the Maxwell demon’s chambers of gas appear effectively not independent from one another to demon’s mind. In turn, the demon is again deceived. This issue is considered in the next section.
4. Non-Unitary Interactions and Macroscopic Variables
The major goal of the present section is to discuss the necessary conditions for providing the thermodynamic limit, i.e. for providing insensitivity to partitioning of a system into subsystems. At first I will consider why the insensitivity to partitioning is important. It is so because the insensitivity to partitioning provides independence from the choice of the auxiliary reference frame introduced for substantiating the partitioning. In turn the independence makes events covariant with respect to time and space. Put it in other words, the covariance implies that the events neither involve nor signal out any special temporal and/or spatial point for their execution. Consequently, neither form of intelligence which is implemented by means of covariant variables would involve any special temporal and/or spatial point and thus makes the corresponding intelligence compatible with the principle of time-translational invariance. It is worth noting that the latter states: no physical process involves special temporal and/or spatial point.
Next it is proven that insensitivity to partitioning takes place at the expense of making relative velocity of molecules a collective variable. In turn the latter proves that the Maxwell demon, this time obeying semantic-type intelligence, is not able to discriminate hotter molecules and thus to utilize fluctuations alone for obtaining information.
It turns out that a necessary condition for insensitivity to partitioning is boundedness. Indeed, suppose that the deviations from local concentrations are bounded. Then, the average over a cell is proportional to the mean with the accuracy that is smaller than the inverse of the cell size as proven in Chapter 1 of [1] .
However, the boundedness over velocities alone is not sufficient to ensure insensitivity to partitioning since, as proven in Chapter 3 of [1] , it yields an amplification of local fluctuations. The latter is so because the traditional approach to interactions assumes interactions among colliding species to be unitary. The latter implies that a certain number of colliding molecules form a closed system during interaction. In turn, the unitarity of the interactions renders mutual independency of the properties of different molecules. Consequently the latter validates the Law of Large Numbers which says that the one can assign probability to a given event which is given by the average of many independent events. However, there is a flaw: being independent from one another, prior to averaging, large enough fluctuations can cause severe damages on each and every system such as pattern formation, sintering, overheating, ageing etc. In any case, the lack of a uniform convergence makes a system to behave in an uncontrolled and non-reproducible way.
In Chapter 3 of [1] I have proposed the way out from the above problem. It assumes that along with the unitary interactions there are non-unitary ones whose role is to dissipate the accumulated energy and matter throughout a system so that to keep local concentrations bounded. This consideration turns sufficient for providing insensitivity to partitioning.
An exclusive generic property of a non-unitary interaction is that it possesses time asymmetry which renders each and every such interaction dissipative. Indeed, the time asymmetry renders the asymmetric role of any molecule that is as follows: the impact of the i-th molecule on the j-th one does not turn out equal to the impact of j-th molecule on the i-th one because we have to take into account the non-equal impact on each of them by a third molecule entering the collision. The non-equal impact of the third molecule entering the collision between i-th and the j-th molecule is an immediate result of the assumption about the independence of the molecules from one another. Thereby the corresponding Hamiltonian turns always into non-Hermitian (its eigenvalues are complex numbers), hence dissipative. On the other hand, we look for a mechanism able to “disperse” every locally accumulated by unitary interactions energy/matter so that the generic dissipativity of the non-unitary interactions to be a key ingredient of that mechanism. The next step is to establish how the dissipated by a non-unitary interaction energy becomes dispersed throughout the corresponding system. I assume that it happens as follows: the dissipated from non-unitary interaction energy resonantly activates an appropriate local linearly-dispersed gapless mode (e.g. acoustic phonon) of the corresponding state variable (e.g. concentration), by means of which “dispersion” of the accumulated matter over the entire system is achieved. Further, the need for stable and reproducible functioning of a system imposes the following general requirement to the operation of that feedback: it must provide those fluctuations covariant, i.e. it must provide independence of the characteristics of each and every of them from their location and moments of their development.
The concept of boundedness {XE “boundedness”}, applied to the operation of the above feedback, implies that it must maintain stability by means of providing the effect of each and every interaction to be always bounded. This implies that whatever the specific characteristics of any given non-unitary interaction are, the operation of the feedback is such that the effect over each and every of the colliding molecule is finite and bounded. This property delineates the fundamental difference between a unitary and a non-unitary interaction. Indeed, whilst the unitaritity implies linearity and additivity of the corresponding interactions at the expense of allowing arbitrary accumulation of matter/energy, the boundedness applied to non-unitarity keeps the effect of any interaction bounded at the expense of introducing non-linearity and non-additivity of its execution. Consequently, the non-unitary interactions are supposed to be modelled by the following 3 generic properties imposed by the boundedness:
1) The Hamiltonian of a non-unitary interaction is described by a non-sym- metric random matrix of bounded elements. The property of being random is to be associated with the interruption of an unitary collision by another molecule at a random moment; and since the original distance to the interrupting molecule is of no importance for any given collision, a non-unitary interaction is not specifiable by metric properties such as the distance between molecules-it is rather specifiable by the current correlations among the interacting molecules so that the intensity of these correlations are permanently kept bounded within metric-free margins.
2) The requisition about limited effect of the interactions over each participating molecule is further substantiated by setting the wave-functions to be bounded irregular sequences (BIS {XE “BIS”}). Indeed, an exclusive property of the BIS’s is that each one is orthogonal to any other; alongside, each of them is orthogonal to its time and spatial derivatives. The latter property is crucial for providing the covariance of the non-unitary interactions since: 1) the orthogonality of every BIS to its spatial and time derivatives provides independence of each and every non-unitary interaction from the interaction path of any participating molecules; in turn, the obtained independence renders every non-unitary interaction a local event, that is: it depends on current status of participating molecules only; 2) alongside, the orthonormality of the BIS’s renders the probability for finding a molecule independent from its current position, and from the position of its neighbors. The proof about orthonormality of BIS can be found in Chapter 3 of [1] .
3) In order to keep the effect of non-unitary interactions permanently bounded and covariant, I suggest that the transitions introduced by them are to be described by operations of coarse-graining {XE “coarse-graining”}. The coarse-graining is mathematical operation which under boundedness acquire novel meaning: it acts non-linearly and non-homogeneously on the members of BIS under the mild constraint of maintaining their permanent boundedness alone. To remind the traditional coarse-graining implies averaging over a partitioned system. Thus, under boundedness the mathematical operation of coarse- graining acquires much wider scope. As discussed in Chapter 1 of [1] , this makes a set of BIS`s dense transitive set where the coarse-graining appears to be an operation that transforms one BIS into another. Thus, the self-consistency of the frame is achieved: the eigenfunctions are supposed always to be BIS and the transitions described as operations of coarse-graining sustain that property since an operation of coarse graining transforms one BIS into another.
Further in Chapter 3 of [1] it is proven that the eigenvalues of any bounded non-Hermitian Hamiltonian tend to cluster near unit circle and their angles are uniformly distributed.
A detailed analysis of the above listed generic properties of the non-unitary interactions, obtained results and proofs can be found in Chapter 3 of [1] .
The clustering of the eigenvalues at the unit circle provides not only boundedness of the amplitude of each fluctuation but boundedness of the rate of development of a fluctuation. Indeed, the rate of a fluctuation is given by the real part of any eigenvalue and thus it is not only bounded but covariant as well;
alongside the corresponding rate of its development is given by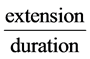 ; the
; the
duration is given by the imaginary part of the corresponding eigenvalue ImEi and its spatial extension is also related to the imaginary part of the same eigenvalue trough the dispersion relation of the excited mode; since it is assumed that the feedback operates through excitation of linearly dispersed gapless modes
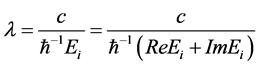 ; thus the extension length is
; thus the extension length is
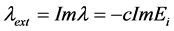 ; thereby the rate of development
; thereby the rate of development 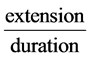 is proportional
is proportional
to the velocity of the acoustic phonons c. Note that the independence of the rate of development from the size of the fluctuation, from the particularities of the interactions and from the moment and location of its development renders its covariance.
The above presented results serve as proof for existence of natural mechanism for maintaining the stability of a system by means of permanent preventing accumulation of arbitrary large amount of matter and energy. The presence of non-unitary interactions along with linearly dispersed gapless modes such as acoustic phonons in every many-body system renders the feedback universally available. We have proved that the operation of that mechanism under boundedness renders fluctuations covariant, extended to bounded size both in space and in time objects which appear, develop and relax with bounded rate.
It should be stressed on the fact that the matter about the covariance of the internal fluctuations for out-of-equilibrium systems is discussed for the first time in the present paper. So far this matter has been taken for granted under the assumption that a fluctuation starts and ends at thermodynamic equilibrium which is assumed a global attractor for all initial states.
It is an immediate consequence of the above considerations that the velocity of the molecules involved in a fluctuation is also constant and thus neither molecule is accelerated or retarded during relaxation. Indeed, it is obvious that the rate of dispersion is sustained bounded if and only if the dissipative energy is kept on the unit circle; if otherwise, the gradual dispersion of energy would provide permanent acceleration of molecules that take part into each fluctuation; it
is best seen by the permanent increase of the rate of dispersion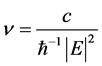 . In
. In
turn, this destabilizes the corresponding system and yields its explosion. Along with heating up, there would be an accelerating expansion of the molecules that participate to each fluctuation. Indeed, the current velocity of each molecule is:
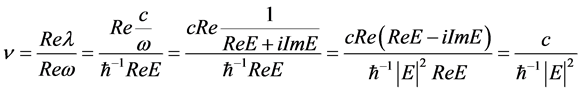 (2)
(2)
In consequence any decrease of 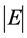 yields acceleration of the corresponding molecules. In turn the latter would produce violation of energy conservation since both the kinetic energy and the heat grows up to infinity each starting from any finite value; hence each and every fluctuation, regardless how small it could be, would yield system breakdown. On the contrary, the maintenance of the energy on the unit circle guarantees constant velocity of the corresponding molecules during the process of damping out of each and every fluctuation. Alongside this smoothing out happens at constant temperature since keeping energy uniformly distributed along the unit circle implies constant relative velocity among molecules which in turn sustains constant temperature. Consequently, damping out of fluctuations does not produce or consume heat. Accordingly, both temperature and concentrations turn out to be properties of the corresponding homeostasis.
yields acceleration of the corresponding molecules. In turn the latter would produce violation of energy conservation since both the kinetic energy and the heat grows up to infinity each starting from any finite value; hence each and every fluctuation, regardless how small it could be, would yield system breakdown. On the contrary, the maintenance of the energy on the unit circle guarantees constant velocity of the corresponding molecules during the process of damping out of each and every fluctuation. Alongside this smoothing out happens at constant temperature since keeping energy uniformly distributed along the unit circle implies constant relative velocity among molecules which in turn sustains constant temperature. Consequently, damping out of fluctuations does not produce or consume heat. Accordingly, both temperature and concentrations turn out to be properties of the corresponding homeostasis.
The consistency between the assumption about the statistical independence of molecules and the result that the relative velocity turns a collective variable is a result of highly non-trivial interplay between the unitary interactions which provide statistical independence of molecules and the non-unitary interactions which make the relative velocity collective variable.
Outlining, it is proven that the necessary and sufficient conditions for providing covariance of the macroscopic thermodynamic variables such as temperature and concentration render constant relative velocity among molecules which does not change under damping out of fluctuations. In turn, the demon is again deceived: it cannot produce work out of fluctuations alone.
It should be stressed on the consistency between the ban over information perpetuum mobile and the robustness of the relative velocity of the molecules to damping out of fluctuations. Indeed, the fact that the relative velocity is not affected by damping out fluctuations makes the macroscopic variables such as temperature and concentration to be characteristics of the homeostasis. Then, any their change is to be associated only with changes in the current homeostasis. Then, since macroscopic variables sets the properties of the cycle executed by every non-mechanical engine, it is obvious that the useful work which is a measure about the obtained information, is result of changes in homeostasis alone. In turn, this opens the door to another formulation of the ban over information perpetuum mobile: acquiring information is available only if there are changes in homeostasis. In turn, the latter constitutes the major advantage of the new approach: it puts the decomposition of the response to a self-organized pattern and a noise component with universal properties as its central property. Moreover, it allows a system to reside in more than one homeostatic state which is in sharp contrast with the traditional statistical theory where a system resides only in a single state called equilibrium.
5. Ban over Acquiring Information from Fluctuations Alone
The major goal of the present paper is to summarize the obtained above result that information cannot be acquired from fluctuations alone. This problem is set by challenging the Maxwell demon’ super-intelligence which challenging started in Section 2. There I have demonstrated that in the frame of the traditional approach the demon’ super-intelligence turns out to be model dependent and in view of the ill-defined average velocity, the demon is deceived at almost each trail. Further, obeying different intelligence, namely a semantic-like one, the relative velocity turns out to be a collective variable and the demon again turns unable to utilize fluctuations for obtaining any information.
At first sight it seems that the demon’ intelligence is in impasse: both approaches make the demon unable to produce information from fluctuations alone. However, this impasse is rather advantage than a setback since it makes the ban over information perpetuum mobile model-independent. Put it in other words, this ban does not depend on the type of intelligence which the demon possesses. In turn this property constitutes the fundamental value of that ban: its independence from the type of intelligence involved.
I do not discuss the matter about information coding by continuous fields such as e.g. electromagnetic one, because of the following reasons: 1) continuous fields obtain capacitance of continuum which implies that there not countable. The latter implies that infinite (and uncountable) amount of energy/matter/infor- tion can be stored within smallest volume and continuously extracted/added from there without limits. This assumption, however, contradicts our daily experience which shows that the stability of each and every system has specific limits; 2) the continuity of fields renders structure and functionality of any object extremely fragile to the tiniest internal fluctuations and environmental variations.
Similar reasons apply to the consideration of neural networks as grounding model for complex systems. The role of fields for neural networks is played by the probability for finding a node in a given state. The problem is that this probability is artificially set apriori by an external agent that is by a human mind. In result, no structure would be organized in an autonomous way. Moreover, even certain self-organization is available it would be enormously fragile to tiniest noise, both internal and environmental one. On the contrary, an exclusive property of boundedness proven in Chapter 1 of [1] is that the existence and robustness to noise of a homeostatic pattern is independent from the statistics of environmental variation and internal fluctuations if only they are kept within specific margins. Thus, the notion of homeostatic pattern acquires the property of robustness to fluctuations in an autonomous, self-organized way.
Let me now discuss the problem about overheating which persists at the traditional approach. This problem commences from two reasons: 1) since the hardware executes arbitrary algorithms, it is impossible to prevent overheating if not special precautions are taken; 2) it is impossible to prevent overheating due to halting problem since it is impossible apriori to judge whether a given algorithm halts. This leads to conclusion that no Turing machine is in balance with its environment.
On the contrary, the semantic-like organization of the response is always in balance with its environment. This is due to the fact that semantic trajectories form bounded irregular sequences (BIS) whose exclusive property is that their variance is always bounded. In turn, this keeps heating within specific for each system margins. Moreover, the generic property of the decomposition of each and every response to the homeostasis and noise happens with the constant accuracy. This result, proven in [1] , implements the ban over transformation of noise into information.
At this point it is worth noting that the presence of non-recursive component is fundamental outcome from the highly non-trivial role which the stability of information plays. It is obvious that without bounded noise it is impossible to have any non-recursive component and thus all specific properties would be expressed by recursive means only concentrated in the corresponding homeostatic pattern alone. However, it is well known that the stability of any specific pattern alone (i.e. without noise) is provided only in specific steady environment. On the other hand, the stability of information in an ever-changing environment is provided by the presence of noise component as an indispensable part of each and every response since the noise implements the mechanism of dissipation of local exceeds of matter/energy/information. The two-fold outcome of this setting is as follows: 1) the presence of noise keeps the local m.s.d. within given margins and thus does not allow temporary overheating; 2) the presence of noise implements universal mechanism for dissipation of local exceeds of matter/energy and provides robustness of homeostasis to environmental fluctuations. In turn this renders appropriateness of the association of the notion of information symbol with the notion of a homeostatic pattern since now each and every information symbol acquires autonomy, i.e. it becomes robust to environmental variations. Further, a generic property of the decomposition of the response to homeostasis and noise is the constant accuracy with which that happens. In turn, that robustness implements the ban over information perpetuum mobile since it does not allow any transformation of noise into information.
An important consequence of the ban over information perpetuum mobile is the fact that it produces ban over acquiring absolute knowledge which turns out to be also model independent. Let me now demonstrate how ban over absolute knowledge appears in both the traditional approach and in the setting of concept of boundedness. In the setting of boundedness the ubiquitous presence of noise component, necessary for sustaining stability of any current homeostasis, along with the ban of transformation of that noise into information limits acquiring of information up to the knowledge of current homeostasis. In the frame of the traditional approach the role of noise band is played by the mutual information. Indeed, the Shannon coding theorem proves that accuracy of transmitting information never exceeds the corresponding mutual information even in a noiseless channel. In turn, this proves the model independence of the ban over acquiring absolute knowledge. Yet, the fundamental advantage of the setting of boundedness is that the constant accuracy of the separation of homeostasis and noise renders obtained information reliable, though incomplete, on the contrary to the traditional approach where correlation coefficient varies currently throughout a message and thus one is not able to decode any piece of information in a reliable way.
6. Conclusions
The major goal of the present paper is to demonstrate the model-independence of the ban over information perpetuum mobile. It has been proven that it is shared by both the traditional statistical approach and the newly introduced theory of boundedness. The fundamental implication of that model independence is its generalization to a ban over gaining absolute knowledge. This infers that every type of intelligence has its limits. Alongside, this implies that any piece of information is obtainable if and only if the system not only dissipates some heat but undergoes structural and functional changes. In turn, the response of a system acquires exclusively for the boundedness property of being decomposable into two parts: a robust pattern to environmental variations homeostatic pattern and a noise component. An exclusive property for the boundedness is that it provides the noise component with universal characteristics robust to noisy statistics. This provides that the decomposition of the response happens with constant accuracy in an ever-changing environment. Consequently, this constitutes the major advantage of the setting of boundedness: it renders the knowledge of each homeostatic pattern unambiguously obtainable and reproducible in an ever-changing environment subject to the constraint of boundedness alone. To compare, reproducibility of any law (information) in the setting of the traditional statistical approach requires also exact reproducibility of the environment. This constitutes a demarcation between the boundedness and the traditional statistical approach: obtaining information in the setting of boundedness proceeds so that each system “hardware”-environment is in balance on the contrary to the traditional statistical approach where obtaining of any information puts the system “hardware”-environment out of balance unless special artificial precautions are undertaken. Yet, in both cases it is impossible to acquire knowledge out of fluctuations alone which constitutes the model independence of the ban over information perpetuum mobile. Alongside, the ban over information perpetuum mobile has a wider scope since the inevitable presence of noise renders impossible acquiring of absolute knowledge. Thus, the knowledge is obtainable up to the knowledge about current homeostatic pattern. Yet, its exclusive property to be obtainable with constant accuracy and to be insensitive to the details of an ever-changing environment renders the obtained information reliable and available for middle-term predictions.