1. Introduction
The poly-crystal silicon thin films have excellent photo-electric properties and production of low cost in the field of energy and informational industry, become a very important electronic materials, widely used in the integrated circuits, semiconductor devices and solar energy cells production. The manufacturing technique includes oxidation, diffusion, alloy and etc. [1] [2] , in the diffusion process, the diffusing chamber is an important equipment for diffusion gas supplying and reacting, and its temperature and flow rate control are the key technologies for poly-crystal silicon thin film production. One kind of overall structure of diffusing chamber control devices is shown as Figure 1.
The diffusing chamber is axis symmetric and separates the inner part, which contains the deposited wafers and the diffusion gas, and the lamp heaters are uniform annular which distributed on the inner part; also the chamber internal wall is coated with reflective layer. The deposited wafers are partitioned into concentric elements and are coaxial with the chamber. The temperature is sensed at twelve locations across the wafers along the cylindrical axis of the chamber.
In the production, the chamber temperature should be easily operated with given control parameters of the gas temperature and flow rate, and its product process satisfies the following technical requirements:
1) The diffusing chamber is vacuum condition before ventilating diffusion gas;
2) To ensure the purity of the diffusion gas, the ventilating pipelines and chamber need purify after an operating cycle, meanwhile, it satisfies the function of gas automatic to be replenished in the production;
3) Achieving rapid variable temperature and flow rate adjustment, satisfying the technical indicators of poly-crystal silicon thin film production;
4) The control process of all the electric actuators can be operated with manual and automatic control modes, and the control processes are conveniently, safety and reliable for user operating.
In Figure 1, it is a difficult control system that there are two control targets
![]()
Figure 1. The overall structure of control device.
and two complex coupling variables with modeling uncertainties, errors and disturbances. There is a need to develop a mathematical model that takes into accounts the combined dynamics of diffusion gas flow rate and heaters power, and a method for high-performance rapid variable temperature control with strong robustness. For the chamber control theory and application, there were many results in the past few decades [3] - [11] , such as using traditional PID control method to solve the temperature tracking in [3] ; by using linear programming techniques, Norman [4] formulated and solved the problem of minimizing the worst error in the wafer temperature control. To ensure deposited wafer temperature trajectory tracking, model-based control presented in [6] [7] [8] , but these control methods were based on the exact mathematical modeling, therefore, they may not be applicable in an actual rapid thermal processing system in the presence of modeling uncertainties, disturbances, errors and etc.. To overcome the modeling errors, Lai and Lin [9] applied neural fuzzy network to temperature control in a rapid thermal processing system, then, Jin and Hyun [10] proposed a neural network iterative learning controller to compensate the mathematical model errors, and achieved an accurate output tracking by experiment and simulation. Based on iterative learning control, Yang et al. [11] designed a quadratic-optimal learning control method and implemented on an experimental RTP system despite existed disturbances and model errors.
Recently, scholars and engineers have presented some novel control techniques for thermal processing in the industry application [12] [13] [14] [15] . Based on BP and GA technologies, Zhang et al. [12] reduced the static temperature compensation and temperature drift. Li et al. [13] used a novel state space model predictive method to solve the industrial furnace temperature control. For dynamic temperature compensation, Qiao and Chai [14] proposed an intelligence-based temperature switching control implemented in the raw meal production. To eliminate the coupling effect, an intelligent PID decoupling control system integrating self-growing radial basis function neural network was proposed in [15] . Compared with the aforementioned results, based on PLC hardware configuring, this paper designs the H∞ variable temperature control and Expert PID flow rate control in the diffusing chamber; the temperature control synthesizes their advancements in the static temperature drift and dynamic disturbances attenuation, meanwhile, the system modeling uncertainties, errors and unknown disturbances are adequately considered. Through numerical simulations and actual application, it demonstrates that the present control strategy is effective.
The remaining parts of this paper are organized as follows:
Section 2 detailedly introduces the system control hardware configuring design, which applies programmable logic controller and its function modules to configure control hardware system for the control. Section 3 describes the control strategies and programs design for the chamber control processing, the pro- cessing control simplified flow chart is shown in Figure 2, furthermore, designs the HMI for user conveniently operating. Lastly, in section 4 the designed control
![]()
Figure 2. The production control flow chart.
system performances are simulated and analyzed in the actual production.
Notations: The notation used throughout the paper is fairly standard. 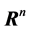 and
and 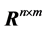 denote the n-dimensional Euclidean space and the set of all n × m real matrices, respectively; I is the identity matrix with appropriate dimension. The superscript T represents the transpose of a matrix;
denote the n-dimensional Euclidean space and the set of all n × m real matrices, respectively; I is the identity matrix with appropriate dimension. The superscript T represents the transpose of a matrix; 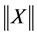 refers to Euclidean norm of the vector X. The notation P > 0 means that P is real symmetric and positive definite. In symmetric block matrices, the
refers to Euclidean norm of the vector X. The notation P > 0 means that P is real symmetric and positive definite. In symmetric block matrices, the 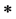 asterisk represents a term that is induced by symmetry. Matrices, if their dimensions are not explicitly stated, are assumed to be compatible for algebraic operations.
asterisk represents a term that is induced by symmetry. Matrices, if their dimensions are not explicitly stated, are assumed to be compatible for algebraic operations.
2. System Control Hardware Design
2.1. System Control Hardware Configuring
In accordance with the system devices (Figure 1) and the flow chart (Figure 2), the temperature and flow rate control have 4 analogues and 6 digital input signals, respectively, with the additional 28 output control signals. The system hardware control main modules applies a compacted Siemens PLC (CPU 314 C-2 DP) [16] , affiliates 2 digital input/output (DI/DO) modules (C1_2 and C2), one analogue/digital (AI/DI) signals input module (C_1), one power module and one HMI (MP277 10#) to configure; The system control hardware configuring satisfies the control output of the valves, pumps, power driving boards and heaters, the construction of system control hardware is shown in Figure 3.
2.2. The Hardware’s Input and Output (I/O) Ports Definition
According to Figure 3, defining the I/O ports function of the module C1_1, C1_2 and C_2 are shown in Figures 4-6, respectively.
2.3. Temperature Sampling and Driving Circuit Design
Considering the system cost, in order to reduce the number of input modules, the temperature analogue sampling and driving circuit design, which uses of 12 high-precisely thermal couple AD590s monitoring the temperatures of wafers, applies a piece of MC74HC4514N decoder chip constructing analogue signals switches, then through a precisely 1 kΩ resistance and an isolating amplifier converting the analogue signals to current (0 - 20 mA) sent to the 14th and 15th ports of module C1_1, the signal sampling detection uses periodic refreshing mode, the circuit design is shown in Figure 7.
![]()
Figure 4. Module C1_1 I/O ports function.
3. System Control Strategy and Program Design
In this section, the system control strategies and program flow chart design will be presented. The system adopts manual and automatic operating modes in terms of the requirements of production process, this paper only presents the automatic control mode design.
3.1. System Program Flow Design
Based the control flow chart (Figure 2) and production technical requirements,
![]()
Figure 5. Module C1_2 I/O ports function.
the designed main control program flow include temperature and flow rate analogue detecting control, Modbus communication, valves control, heating control, exhaust purifying, leakage testing and diffusion gas filling subroutine modules, the systems applies circular scanning output to carry out work, the main program flow chart is shown in Figure 8.
3.2. Temperature Interrupt H∞ Control
In Figure 1, by the first law of thermal-dynamics, the temperature dynamic
![]()
Figure 7. Temperature sampling & driving circuit.
model of the diffusing chamber is
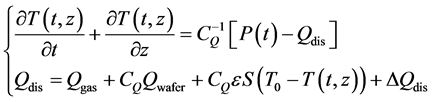 (1)
(1)
where 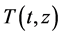 is the temperature distributing vector of internal chamber,
is the temperature distributing vector of internal chamber, 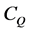 is the parameter of heat capacity matrix,
is the parameter of heat capacity matrix,  is the coefficient matrix of heat conduction for the chamber’s internal and external temperatures and S is heat transfer area.
is the coefficient matrix of heat conduction for the chamber’s internal and external temperatures and S is heat transfer area.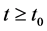 ,
, 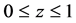 ,
, ![]() is the external temperature of chamber,
is the external temperature of chamber, ![]() is the condition of temperature boundary values,
is the condition of temperature boundary values, ![]() is the initial temperature.
is the initial temperature. ![]() is the heaters output power.
is the heaters output power. ![]() is the systems’ synthetic diffusing heat energy, in which
is the systems’ synthetic diffusing heat energy, in which ![]() is the diffusion gas absorbed heat energy,
is the diffusion gas absorbed heat energy,
![]() (2)
(2)
where ![]() is the diffusion gas flow rate,
is the diffusion gas flow rate, ![]() is the diffusion gas specific heat capacity.
is the diffusion gas specific heat capacity. ![]() is the radiation heat energy absorbed by the wafer and
is the radiation heat energy absorbed by the wafer and
![]() (3)
(3)
where ![]() and m are the wafer specific heat capacity parameter and mass, respectively.
and m are the wafer specific heat capacity parameter and mass, respectively. ![]() is the unknown heat energy and
is the unknown heat energy and ![]() is the norm bounded uncertainties which can be depicted the following,
is the norm bounded uncertainties which can be depicted the following,
![]() (4)
(4)
where H and E are known constant matrices, ![]() is the Lebesgue measurable time varying matrix and satisfies
is the Lebesgue measurable time varying matrix and satisfies
![]() (5)
(5)
Considering the actual structure of chamber and the heating mode in Figure 1, the inner wall of chamber is assumed as a gray, diffuse, opaque surface, the heat absorbed of all the wafer elements is also assumed to be equal, which can be thought the temperature distribution is uniform of the inner part of chamber, that is
![]() (6)
(6)
Assuming ![]() is the measured temperature, then the dynamic model (1) is simplified to
is the measured temperature, then the dynamic model (1) is simplified to
![]() (7)
(7)
set ![]() is the error of actual temperature and the expected control values, system disturbances is
is the error of actual temperature and the expected control values, system disturbances is![]() ,
, ![]() is the heaters control output power, then from (1) to (7) the dynamic model can be written as
is the heaters control output power, then from (1) to (7) the dynamic model can be written as
![]() (8)
(8)
where![]() , the
, the ![]() is delay time of measured temperature and
is delay time of measured temperature and
![]() (9)
(9)
In order to reduce the control cost to be enough small with the uncertainties and disturbances, that is
![]() (10)
(10)
where Q and R are positive weight matrices, respect to the important degree of attenuating temperature error and control cost. Then defining the temperature control optimal object evaluating equation as
![]() (11)
(11)
where![]() ,
,![]() .
.
Then from (10) to (11), the control optimal object equation is equivalent to
![]() (12)
(12)
where ![]() is a positive scalar. For system (1) design controller as
is a positive scalar. For system (1) design controller as
![]() (13)
(13)
where K is the controller gain, which will be designed, from (7) to (13), obtains
![]() (14)
(14)
where![]() .
.
Remark 3.1: In system (7), the is depicted the time varying unknown thermal energy which caused by the diffusing chamber’s temperature modeling uncertainties and errors, without loss of generality, which the uncertainties and errors have several aspects, such as the diffusion gas modeled uncertainties, the gas thermal decomposition energy, convection heat, unknown heat energy disturbance and etc..
The temperature dynamic mode (8), as an applied control systems design [17] , in order to surmounted the uncertainties, errors and unknown disturbances, firstly, in this paper we casts H∞ control strategy to put forward a sufficiently condition of system (8) robustly mean square stable as the following definition.
Definition 3.1: For diffusing chamber’s temperature system (8), under the controller ![]() and given positive scalar
and given positive scalar![]() , if there exist positive definite symmetric matrices P, N, satisfy the following inequality (15), then the closed-loop system (14) is robustly mean square stable, and satisfies
, if there exist positive definite symmetric matrices P, N, satisfy the following inequality (15), then the closed-loop system (14) is robustly mean square stable, and satisfies ![]() ,
,
![]() (15)
(15)
Proof: considering the following Lyapunov function
![]() , (16)
, (16)
with![]() , a straightforward computation gives the time derivative of (14) along the solutions of (8) as
, a straightforward computation gives the time derivative of (14) along the solutions of (8) as
![]() , (17)
, (17)
where![]() ,
,
so the system (8) is asymptotically stability.
when![]() , defining
, defining
![]() , (18)
, (18)
where![]() .
.
In terms of (15) and (18), applies matrix schur complements theorem [18] , it yields
![]() , (19)
, (19)
with the zero initial condition, there have ![]() and
and
![]() , so there is
, so there is
![]() , (20)
, (20)
the (20) implies![]() .
.
This completed the proof.
Then based on the definition 3.1, the controller parameter solving procedure is presented as the following theorem.
Theorem 3.1: The system (8) is H∞-![]() stabilization, if there exist positive definite symmetric matrices X, Y and scalar
stabilization, if there exist positive definite symmetric matrices X, Y and scalar![]() , satisfies the following linear matrix inequality (21), then the (13) controller parameter is
, satisfies the following linear matrix inequality (21), then the (13) controller parameter is![]() .
.
where
![]()
![]() . (21)
. (21)
Proof: In terms of the definition 3.1, applies linear matrix inequalities theory [18] , the (21) can be obtained from (15) easily, the proof is omitted.
In the aforementioned temperature interrupt H∞ control, as the 12 power driver boards and 12 lamp heaters have the same physical and electrical properties, respectively, therefore, by Modbus communication mode, the temperature analogue signals sampled-data sent to module C1_1 data area, then adopting the H∞ control strategy obtains temperature control signals in the interrupt routine organization block (OB35) at every 100 ms time and outputted from the 15th port of C_2 module, sent to the 12 power driving boards with the same pulse wave modulating form, achieves the 12 lamp heaters power control.
3.3. Flow Rate Interrupts Expert PID Control
For the flow rate control, there are several important influence functions, such as the impulse disturbance of the adjusting valve’s starting and stopping, control signals noise [19] [20] [21] and etc. Assuming the flow rate control error is ![]() and output is
and output is![]() , the flow control system adopts expert PID control strategy, which the flow control chart is shown in Figure 9.
, the flow control system adopts expert PID control strategy, which the flow control chart is shown in Figure 9.
In Figure 9, the k-th error sampled-data filtering output is
![]() (22)
(22)
where ![]() is the (k-1)-th filtering output,
is the (k-1)-th filtering output, ![]() , T is sample time, d is constant time.
, T is sample time, d is constant time.
There are five cases for the expert decision processing of flow rate control:
Case 1: if![]() , then the controller output is max (or min), the control system is equivalent to opened-loop control;
, then the controller output is max (or min), the control system is equivalent to opened-loop control;
Case 2: if ![]() and
and![]() , the error is varying to absolute value increase, then the controller is
, the error is varying to absolute value increase, then the controller is
![]() (23)
(23)
Case 3: if ![]() and
and ![]() or
or![]() , the error is varying to absolute value decrease or reaches equilibrium state, then the controller output is similar to the (23);
, the error is varying to absolute value decrease or reaches equilibrium state, then the controller output is similar to the (23);
Case 4: if ![]() and
and ![]() and
and![]() , then the controller output is
, then the controller output is
![]() (24)
(24)
Case 5: if![]() , the error absolute value is to be enough small, then the controller adds integration part, reduces the stable error.
, the error absolute value is to be enough small, then the controller adds integration part, reduces the stable error.
Remark 3.2: In Figure 9, the filter is first-order limited amplitude average principle, that is, after the ![]() sampled k times, removes the two biggest sampled-data, then obtains the average value for the rest of the k-2 sampled-data, to overcome the effect of signals impulse and peak disturbance, yields
sampled k times, removes the two biggest sampled-data, then obtains the average value for the rest of the k-2 sampled-data, to overcome the effect of signals impulse and peak disturbance, yields ![]() sent to expert PID controller, obtains the flow rate control signals in the interrupt routine organization block (OB34) at every 100 ms time and outputted from the 16th port of C_2 module with the pulse wave modulating form, control the adjusting valve.
sent to expert PID controller, obtains the flow rate control signals in the interrupt routine organization block (OB34) at every 100 ms time and outputted from the 16th port of C_2 module with the pulse wave modulating form, control the adjusting valve.
3.4. HMI Control Design
In this control system, applies the Siemens MP277 10# HMI as user operating interface, according to the user operating and requirements of production processing, the designed main operating interface is showed in Figure 10, which mainly includes the alignment operating control of valves, pumps and heaters as shown in Figure 11, the temperature and flow rate control user interface as shown in Figure 12, the temperature and flow rate trends interface.
4. Application and Control Analysis
In this section, the system control simulating and effective application are given and analyzed. The deposited wafers are assumed to be opaque.
Example 1. One type of poly-crystal silicon thin film which deposited on the glass substrate, its production need the SiH4 gas temperature maintained in 200˚C (Celsius degrees) and flow rate in 0.085 liters per second. The chamber temperature need be controlled error within 1˚C and the flow rate controlled within 5 seconds to achieve the set values of production. Some physical parameters of the diffusing chamber and SiH4 gas are given in Table 1.
Set Q = 2.5, R = 1.0, ![]() ,
, ![]() ,
, ![]() and the chamber external temperature
and the chamber external temperature![]() , using Matlab control toolbox [18] to solve (21), obtains the output power u(t) is 0.2903 kw・˚C.
, using Matlab control toolbox [18] to solve (21), obtains the output power u(t) is 0.2903 kw・˚C.
The temperature and flow rate control simulating performances which compared with traditional control methods [22] [23] [24] are shown in Figure 13 and Figure 14, respectively.
Example 2. The other kind of poly-crystal silicon thin film production need the temperature in 630˚C and flow rate in 0.15 liters per second, the chamber temperature should be controlled error within 2˚C and the flow rate controlled within 5 seconds, deposited on the Si substrate. Some physical parameters of the chamber and SiCl4 gas are given in Table 2.
when Q = 25 and R = 10, ![]() ,
, ![]() ,
, ![]() and chamber external
and chamber external![]() , obtains the output power u(t) is 0.3425 kw・˚C. The designed temperature and flow rate control system performances are simulated as shown in Figure 15 and Figure 16.
, obtains the output power u(t) is 0.3425 kw・˚C. The designed temperature and flow rate control system performances are simulated as shown in Figure 15 and Figure 16.
![]()
Table 1. Physical parameters in case 1.
![]()
Table 2. Physical parameters in case 2.
In Figure 15 and Figure 16, the designed control system simulating results show the flow control quickly, achieve control object thereabouts 5 seconds, due to the inertial effect of temperature which regulates 12 heaters power output reaching 630˚C at least 8 seconds, and temperature error within 1˚C (a group of actual control parameters are shown in Figure 12). The actual temperature and flow trends are shown in Figure 17 at different time scale (temperature and flow trends output from the left and right axis respectively, where temperature trend indicates the average values of the 12 zones temperature).
In this case, we check the control capability of the proposed controller when the chamber temperature varies from 630˚C to 800˚C at 20 seconds scale in the production. The temperature control trajectory is shown as Figure 18.
![]()
Figure 17. The temperature and flow trends in the HMI.
![]()
Figure 18. The control trajectory of varying temperature.
Furthermore, in example 2, considering the system physical parameters perturbed by 10%, and the temperature varies from 630˚C to 1100˚C at 15 seconds scale, then decreases to 660˚C at 30 seconds scale in the production, we apply the H∞ control scheme and expert PID to the perturbed system. Figure 19 shows the result of the variable temperature trajectory.
From the Figure 19, we can know that the temperature variable rates are about 80˚C・s−1 and 70˚C・s−1 from 20˚C ramp up to 630˚C and 1100˚C, respectively, then decreasing rate is about 50˚C・s−1 from 1100˚C to 800˚C. Based hardware configuring, compared with last results, our method is therefore able to cope with system perturbations, errors and uncertainties adequately, overcomes the shortcomings of the traditional methods, reduces the system control oscillation and overshoot, improves the robustness of system and economizes power when applied to the actual system
5. Conclusion
In this paper, the diffusing chamber’s gas temperature and flow rate control are
![]()
Figure 19. The temperature trajectory of parameter perturbed.
designed for poly-crystal silicon thin film production, and we apply Siemens PLC modules to build the mainly control hardware system. For diffusing chamber temperature, this paper designed expert PID controller to adjust the diffusion flow rate and H∞ control strategy to control 12 zones heaters power, to achieve rapid variable temperature. The user can easily and conveniently operate the production control by designed HMI. Lastly, the designed control system are simulated and applied in the actual production, and results show that the system control satisfies the requirements of production techniques and indicators for poly crystalline silicon thin film.
Acknowledgements
This work is supported by the Jiangsu Overseas Research & Training Program for University Prominent Young & Middle aged Teachers & President (2012- 2015).