Application of Flood Routing Model for Flood Mitigation in Orashi River, South-East Nigeria ()
1. Introduction
When it rains or snows, some of the water generated is retained by the soil depending on the degree of dryness of the soil, some are absorbed by vegetation, some evaporate and the remainder, which reaches stream channels, is called runoff. Flood is an unusual accumulation of water above the ground, which is caused by high tides, heavy rainfall or rapid runoff from paved surfaces [1] . Floods occur when soil and vegetation cannot absorb all the water; water then runs off the land in quantities that cannot be carried in stream channels or retained in natural ponds and constructed reservoirs. About 30 percent of all precipitation is runoff, and this amount may be increased by melting snow masses. Periodic floods occur naturally on many rivers, forming an area known as the flood plain. These river floods often result from heavy rain, sometimes combined with melting snow, which causes the rivers to overflow their banks; a flood that rises and falls rapidly with little or no advance warning is called a flash flood. Flash floods usually results from intense rainfall over a relatively small area. Coastal areas are occasionally flooded by unusually high tides induced by severe winds over ocean surfaces.
In Nigeria alone, it is estimated that approximately 12% of the land area is within the 100-year flood plain [2] . However, the percentage of urban and rural areas within the flood plain is much higher (about 20%). The total property value within the flood plain already exceeds hundreds of millions of Naira and is growing at a rate of about 5% per annum. Flood disasters have increased tremendously everywhere in Nigeria in recent times, resulting to loss of lives and properties, rendering, thousands homeless, and disruption of economic activities. Without flood control and adequate drainage structures, the extent of destruction and damage would increase at an even faster pace. There were over 200 floods affecting over 180 million people, 8,000 deaths and over £40 billion in damages in 2007 [3] . It is in fact the most common of all environmental hazards and it regularly claims over 20,000 lives per year and affects around 75 million people worldwide [4] . The result or implication of human development is the evolution of serious environmental problems such as flooding, deforestation, erosion, etc. These environmental problems have prevailed more in the developed and developing nations of the world and urban centers in general. Flooding particularly has caused a lot of the world. Floods cause about one third of all damages from natural disaster [5] . Flood is a body of water which rises to over- flow land, which is normally submergered [6] . They are environmental hazards that occur regularly every year in different parts of the country especially during the rainy season. Flood water overflow expanse of land, submerging the land. Flood occurrence is usually due to the increase inthe volume of water within the water body such as rivers and lakes. This causes water to exceed the drainage channel capacity and overflow its bounds. Flooding occurs also when excess runoff is created owing to the inability of thesoil to infiltrate water or when the soil has reached its field capacity or saturation. The result is excess runoff which submerges the landscape. This form of flooding is particularly the case in most urban centers of the world and Nigeria in particular, where urbanization has dis- turbed or altered the natural process of infiltration.
The main purpose of the study was to apply flood routing models for flood mitigation in South-East Nigeria, also to compare the different methods of unsteady flow modelling using Regression approach. The study was conducted in the Orashi river watershed covering 10,000 km2 and lying between latitudes 4˚15' and 7˚00'N and longitudes 5˚50' and 9˚00'. Natural stream flood routing was performed using different methods for solving the unsteady flow equations in order to compute stages and discharges of wave propagation. The river reach is approximately 8 km long. The channel bed is lined with mostly gravel and large boulders. The Orashi River flows past the Oguta Lake in its southwestern portion. It picks up volume and speed with the extra flow from Njaba River via Oguta Lake before flowing parallel to the River Niger.
Flood Routing impacts the magnitude of the peak discharge, the time of the peak discharge, depth and extent of flooding and environmental factors such as stream bank erosion, flood plain scour, sediment transport and deposition [7] . It is a technique of determining the flood hydrograph at a section of a river by utilizing the data of flood flow at one or more upstream sections. The hydrologic analysis of problems such as flood forecasting, flood protection, reservoir design and spillway design invariably include flood routing. In flood studies and design, the Engineer requires estimates of both the stage and discharge along a water course resulting from passage of a flood wave. The technique of flood routing is used for this purpose [8] . The hydrograph of a flood entering a Reservoir will change in shape as it emerges out of the reservoir, because certain volumes of its water is stored in the reservoir temporarily and is let off as the flood subsides. The base of the hydrograph therefore gets broadened, its peak gets reduced, and, of course, the time of peak is delayed. The extent by which the inflow hydrograph gets modified due to the reservoir storage can be computed by a process known as flood routing [9] . Hydrograph represents how a catchment responds to rainfall [10] .
2. Methodology
The data for this research were collected from National Emergency Management Agency (NEMA), FCT Abuja.
Three flood routing models were comparatively applied including Muskingum model, Level Pool model and Modified Pul’s model.
2.1. Muskingum Method
The graphical procedure consists of generating graphs of [XI + (1 − X)O] vs. S for different values of x, arbitrarily selected such that 0 < X < 0.5. The optimal value of x is selected as that which produces the narrowest and straightest loop graph of 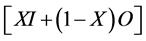 vs. S. The available data for a series of flood events are in flow, outflow and a time increment t for every one hour (3600 s) in the calculation. The first stage of the solution was to find the average inflow and outflow, starting from the second time step. Then to find the change in the reach storage (S) which is the difference between the average inflow and outflow multiplied by the time increment t. Secondly, the cumulative volume of reach storage (Si+1), where (i ranges from one to n) can be found by adding the storage at a previous time step (Si) to the change in storage of the next time step (Si+1).
vs. S. The available data for a series of flood events are in flow, outflow and a time increment t for every one hour (3600 s) in the calculation. The first stage of the solution was to find the average inflow and outflow, starting from the second time step. Then to find the change in the reach storage (S) which is the difference between the average inflow and outflow multiplied by the time increment t. Secondly, the cumulative volume of reach storage (Si+1), where (i ranges from one to n) can be found by adding the storage at a previous time step (Si) to the change in storage of the next time step (Si+1).
Thirdly, a value of x is chosen from 0.1 to 1.0 and the storage (S) is plotted against the weighted flux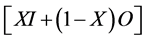 . An Excel spread sheet was used to implement the numerical procedure.
. An Excel spread sheet was used to implement the numerical procedure.
2.2. Level Pool Method
This method involved the use of Storage-Indication to route the inflow hydrograph computed for Orashi River. Storage is nonlinear function of Q.
2.3. Modified Pul’s Method
Hydrographs of 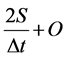 against outflow and a hydrograph of inflow against
against outflow and a hydrograph of inflow against
time were developed. The solution to the Modified Pul’s method was accomplished by developing a graph (or table) of [2S/Δt + O] vs. O. In order to do this, a stage-discharge-storage relationship was derived.
3. Results and Discussions
The inflow and outflow hydrographs of the river reach are tabulated in Table 1. The Attenuation which is the reduction in the peak discharge as it moves downstream could be observed from the Table resulting in a broader flat hydrograph. The value of relative percentage attenuation computed using Equation (1) was 7.09%.
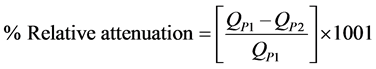 (1)
(1)
where QP1 and QP2 are peakinflow and outflows (m3/s) respectively.
Using the collected data, the mean storage of the river was determined thro- ugh application of mass balance equation.
3.1. Results of the Basic Muskingum Method Application
The data in Table 1 was used to obtain the Muskingum routing parameters k and x for this river reach. The initial storage in the system was 715,000 m3. By applying the storage calculation on a number of flood events storage loops were developed.
X value was taken as 0.15 since the graph of X = 0.15 gave a straight line (see Figure 1). Based on the value of X the Muskingum constant K which indicate the routing period was then computed from the slope of the graph; k = slope of graph = 8205 sec; which was taken as 2.3 hours approximately. This indicated the released period that would allow for effective storage andprevent excessive flood at the downstream section of the river.
![]()
Table 1. Cumulative mean storage at X = 0.15.
![]()
Figure 1. Plot of Weighted flux [xI + (1 − x)O] against Storage.
3.2. Determination of Outflow Values of Orashi River Using the Muskingum Routing Equation
The Muskingum routing procedure was used to route the hydrograph in Table 1.
Since Δt = 1 hr, as suggested by the inflow data. However, check that with the selected Δt, parameter values meet restrictions: X < 0.5 Δt/k < 1 ? X.
For this case: 0.15 < (0.5) (3600)/8205 < 1 − 0.15. Thus, OK. Proceed with routing, by obtaining C1, C2, and C3 using Equations (7) - (9) respectively.
Since K = 2.3 hours, time interval = 1 hours, and X = 0.15
Values of K, t, and X into the Equations (7) - (9)
Applying Muskingum routing Equation:
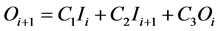 (2)
(2)
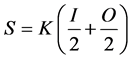 (3)
(3)
But we also have
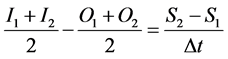 (4)
(4)
Note: Δt = 1 hour = 3600 sec.
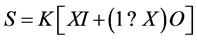 (5)
(5)
where S is storage (m3), K is the travel time in seconds between the two channel sections, O (m3/s) is the outflow (m3/s), I is the inflow (m3/s), and x is a dime- nsion less factor between 0.0 and 0.5 that weights the influence of the inflow and outflow hydrograph to thestorage within the reach.
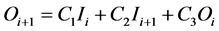 (6)
(6)
where:
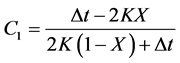 (7)
(7)
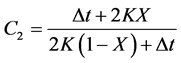 (8)
(8)
 (9)
(9)
C1, C2, and C3 are also known as Courant factors.
The results using Muskingnum method to determine the outflow data are presented in Table 2.
3.3. Level Pool Routing Method
This hydrograph flows into a reservoir whose storage and discharge characteristics are as presented in Table 3. The initial storage in the system is 0 m3 and the initial outflow is 85 m3/s.
For a given set of conditions, the outflow is unique, independent of how that stage is achieved. The peak outflow occurs when the outflow hydrograph intersects the inflow hydrograph.
Hydrographs of 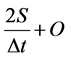 against outflow and inflow against time were pre-
against outflow and inflow against time were pre-
pared. The concept involved development of the function
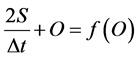
And solving sequentially for every time step.
The following data were relevant in preparing the Table;
・ Elevation vs. Storage
・ Elevation vs. Outflow discharge and hence storage vs. outflow discharge.
・ Inflow hydrograph
・ Initial values of inflow, outflow O, and storage S at time t = 0.
3.4. Modified Pul’s Method
The results using Pul’s method to determine the outflow data for the River are presented in Table 4.
Again, the general continuity equation was adopted. However, in this case, a finite difference form of the continuity equation was used. A graph of [2S/Δt + O] vs. O was derived. In order to do this, a stage-discharge-storage relationship was developed and plotted as a curve. The basic assumption is that a unique and single-valued stage-storage-outflow relationship exists for each reach.
A Summary of measured inflows/outflows and predicted outflows from the three models are presented in Table 5.
The results indicate that Level pool method gave highest value of predicted peak outflow (657 m3/s) while the modified Pul’s method gave the least value (629 m3/s). The derived Regression models are presented in Table 6.
The weighing factor, X value was taken as 0.15.
Based on the value of X, the storage constant K which indicate the routing period was then computed from the slope of the graph; k = slope of graph = 8205 sec; which was taken as 2.3 hours approximately.
![]()
Table 2. Prediction of outflow data of Orashi using Muskingum method.
![]()
Table 3. Orashi River results of outflows for various inflows using Level Pool method.
![]()
Table 4. Results of the Modified Pul’s method for Orashi River.
![]()
Table 5. Summary of Orashi River predicted outflow by Muskingum, Level Pool Routing and Modified Pul’s methods.
![]()
Table 6. Summary of predicted/measured outflow models for Orashi River.
This indicates the released period that will allow for effective storage and prevent excessive flood at the downstream section of the river.
The developed parameter estimation methodology was applied to determine the K, and X values for flow routing corresponding to the river inflow-outflow. The value S of K and X was used to route the flood using three different methods.
From Table 5 and Table 6, it is discovered that the Modified Pul’s method gave a more accurate result of predicted outflow. Modified Pul’s method should therefore be adopted as a model for flood mitigation in Orashi River.
3.5. Design Application of the Modified Pul’s Model to Orashi River
The characteristics of Orashi River Channel are presented in Table 7.
![]()
where I = Inflow (m3/s), O = Outflow (m3/s), Δt = time (s)
Inflow (I) and outflow (O) are functions of time (t), and the storage (S) is a function of the water surface elevation (H) which changes with time (t).
![]() [11] (10)
[11] (10)
where, Y = predicted outflow (m3/s) of Orashi river, x = measured outflow (m3/s) of Orashi river.
The values of measured outflow are shown in Table 5.
Since Inflow is greater than outflow, there will be no flood. A channel that can store 1.26 × 106 m3 is recommended.
The river reach is approximately 8 km long and a sharp crested weir is located 3.93 km from the upstream section of the river. The channel bed is lined with mostly gravel andlarge boulders.
The Orashi River has a trapezoidal cross-section with no recent floodplain [12] . Due to the weir transition downstream the river, a cross-section which is locatedat the upstream end is only considered in modelling.
The nature of the flow in the river Orashi is non-uniform, gradually varied unsteady flow. To determine the regime of flow upstream of the channel, Equation 11wass used to calculate the Froude Number.
![]() (11)
(11)
![]() [13] (12)
[13] (12)
where, V is the average velocity in (m/s) which can be defined from Equation (13), y1 is depth of flow upstream in m and g = 9.81 m/s2.
In channel routing where a non-uniform flow is the case, the average velocity can bedetermined using a reference discharge and the channel cross-sectional area as in Equation (12). To determine the normal depth y0, a reference discharge is selected for a maximumflood event and can be calculated from Equation (13)
Reference discharge, Q0:
![]() (13)
(13)
where Qb = Minimum discharge in (m3/s), Qp = Peak discharge in (m3/s)
![]()
![]()
Therefore, reference discharge is 354 m3/s.
![]()
Table 7. Channel parameters of orashi river.
With the known values of reference discharge (Q0), Manning roughness coefficient (n), Channel bed width and bottom slope, the value of Φ can be determined from Equation (13)
![]() (14)
(14)
![]()
![]()
Upon consulting Table 7 with the above value (![]() ) and with z = 1.25 the value of
) and with z = 1.25 the value of![]() , hence, y0 = 12.34 m, where, b = 22.86 m.
, hence, y0 = 12.34 m, where, b = 22.86 m.
The area of flow A, can then be obtained from Equation (14)
A= [b + (zy0)]y0 × 15
A = [22.86 + 1.25(12.34)] × 12.34
A = 472.44 m2
Hence, Velocity, ![]()
![]()
![]()
Therefore,
![]()
This indicates that the channel has a mild slope and the flow is characterised as gradually varied subcritical flow. The wave celerity (c) can be obtained from the relationship
![]()
where β is assumed to be 0.5 and velocity, V = 0.749
![]()
Therefore, storage = area × velocity × time = 1272700.8 m3.
4. Conclusions
Based on the result obtained from the Orashi flood routing studies, the following conclusions can be made.
・ Three sets of mathematical modeling of Orashi river flood routing based on regression-correlation approach were analyzed namely:
1) Muskingum routing model
2) Level Pool routing model
3) Modified Pul’s model
・ In the Modified Pul’s model, very high and positive values of coefficient of correlation of 0.9984, as well as a standard error of 0.1749 was obtained. This model provided the best-fit curve for the field data.
・ Plots of Modified Pul’s model are in conformity with the field data. They equally agree with literature as follows:
1) During the flood routing, the rate of outflow from the reservoir did not exceed the maximum projected rate of inflow, to the extent possible, which will prevent flooding impacts downstream of the reservoir from being more severe.
2) During the determination of routing parameter, the courant factor did not exceed one, using Modified method.
Since Modified Pul’s method gave the most accurate result of predicted outflow, the method should be adopted as a model for flood mitigation in Orashi River. The design capacity based on this model is 354 m3 which is higher than the routed storage capacity of 348 m3. To guarantee a check against flooding, it is recommended that dredging is carried out to achieve the designed capacity.